RHIC能区Au+Au 碰撞中带电粒子直接流与超子整体极化的计算与分析

江泽方; 吴祥宇; 余华清; 曹杉杉; 张本威

doi:10.7498/aps.72.20222391

摘要

非对心的相对论重离子碰撞中, 不参与碰撞的核子会对参与碰撞的核子产生纵向拖拽, 形成一个相对于纵向倾斜的夸克胶子等离子体(QGP)火球. 同时, 对撞的原子核可将巨大的轨道角动量沉积于QGP中, 使其中的部分子沿系统总角动量方向发生自旋极化. 在光学 Glauber模型基础上, 本文构建了倾斜的三维QGP初态条件, 并结合3+1维黏滞流体力学模型CLVisc, 研究了重离子碰撞的末态带电粒子的直接流和$ \Lambda/\bar{\Lambda} $超子的整体极化. 计算表明, 倾斜的初态条件与流体力学模型的结合能够较好地描述RHIC-STAR实验上观测到的直接流与超子整体自旋极化的数据. 这为人们利用这些观测量进一步约束重离子碰撞产生的核物质的初始几何与运动学状态提供了理论依据.

关键词:

Abstract

In non-central relativistic heavy-ion collisions, the non-colliding nucleons drag the colliding nucleons along the longitudinal direction asymmetrically, producing a longitudinally tilted quark-gluon plasma (QGP) fireball. Meanwhile, these colliding nuclei deposit a huge initial orbital angular momentum into the system, leading to the polarization of partons inside the QGP along the direction of the total angular momentum. Based on the optical Glauber model, we develop a 3-dimensional initial condition of the tilted QGP. By combining it with the (3+1)-dimensional viscous hydrodynamic model CLVisc, we investigate the directed flow of charged hadrons and the global polarization of $ \Lambda/\bar{\Lambda} $ hyperons in heavy-ion collisions. Our calculation indicates that the combination of a tilted initial condition of the QGP and the hydrodynamic model can provide a satisfactory description of the directed flow and global polarization observed at RHIC-STAR. This offers a theoretical baseline for using these observables to further constrain the initial geometry and kinematic properties of the nuclear matter created in heavy-ion collisions.

Keywords:

relativistic heavy ion collision /
quark-gluon plasma /
directed flow /
$ \Lambda/\bar{\Lambda} $ global polarization

作者及机构信息

1.
湖北工程学院物理与电子信息工程学院, 孝感　432000

2.
华中师范大学物理学院, 粒子物理研究所, 夸克与轻子物理教育部重点实验室, 武汉　430079

3.
山东大学前沿交叉科学青岛研究院, 青岛　266237

通信作者: 曹杉杉, shanshan.cao@sdu.edu.cn

基金项目: 国家自然科学基金(批准号: 11935007, 12175122, 2021-867)、广东省基础与应用基础研究重大专项(批准号: 2020B0301030008)、湖北省自然科学基金(批准号:2021CFB272)、湖北省教育厅中青年人才项目(批准号: Q20212703)和教育部夸克与轻子物理重点实验室开放基金(批准号: QLPL202104)资助的课题

Authors and contacts

1.
College of Physics and Electronic Information Engineering, Hubei Engineering University, Xiaogan 432000, China

2.
Institute of Particle Physics and Key Laboratory of Quark and Lepton Physics (MOE), Central China Normal University, Wuhan 430079, China

3.
Institute of Frontier and Interdisciplinary Science, Shandong University, Qingdao 266237, China

Corresponding author: Cao Shan-Shan, shanshan.cao@sdu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11935007, 12175122, 2021-867), the Major Project of Basic and Applied Basic Research of Guangdong Province, China (Grant No. 2020B0301030008), the Natural Science Foundation of Hubei Province, China (Grant No. 2021CFB272), the Young Talents Project of the Education Department of Hubei Province, China (Grant No. Q20212703), and the Open Foundation of Key Laboratory of Quark and Lepton Physics of the Education Ministry of China (Grant No. QLPL202104)

文章全文 : translate this paragraph

参考文献

[1]	Bass S A, Gyulassy M, Stoecker H, Greiner W 1999 J. Phys. G 25 R1 Google Scholar
[2]	Rischke D H, Pürsün Y, Maruhn J A, Stoecker H, Greiner W 1995 Acta Phys. Hung. A 1 309 Google Scholar
[3]	Bozek P 2022 Phys. Rev. C 106 L061901 Google Scholar
[4]	Bozek P 2012 Phys. Rev. C 85 034901 Google Scholar
[5]	Jiang Z F, Cao S S, Wu X Y, Yang C B, Zhang B W 2022 Phys. Rev. C 105 034901 Google Scholar
[6]	Jiang Z F, Yang C B, Peng Q 2021 Phys. Rev. C 104 064903 Google Scholar
[7]	Shen C, Alzhrani S 2020 Phys. Rev. C 102 014909 Google Scholar
[8]	Ryu S, Jupic V, Shen C 2021 Phys. Rev. C 104 054908 Google Scholar
[9]	Wang H, Chen J H 2022 Nucl. Sci. Tech. 33 15 Google Scholar
[10]	高建华, 黄旭光, 梁作堂, 王群, 王新年 2023 72 072501 Gao J H, Huang X G, Liang Z T, Wang Q, Wang X N 2023 Acta Phys. Sin. 72 072501 (in Chinese)
[11]	Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 Google Scholar
[12]	Liang Z T, Wang X N 2005 Phys. Lett. B 629 20 Google Scholar
[13]	孙旭, 周晨升, 陈金辉, 陈震宇, 马余刚, 唐爱洪, 徐庆华 2023 72 072401 Sun X, Zhou C S, Chen J H, Chen Z Y, Ma Y G, Tang A H, Xu Q H 2023 Acta Phys. Sin. 72 072401 (in Chinese)
[14]	浦实, 黄旭光 2023 72 071202 Pu S, Huang X G 2023 Acta Phys. Sin. 72 071202 (in Chinese)
[15]	尹伊 2023 Accepted Yin Y 2023 Acta Phys. Sin. this volume Accepted (in Chinese)
[16]	Huang X G, Huovinen P, Wang X N 2011 Phys. Rev. C 84 054910 Google Scholar
[17]	Li X W, Jiang Z F, Cao S S, Deng J 2023 Eur. Phys. J. C 83 96 Google Scholar
[18]	Alzhrani S, Ryu S, Shen C 2022 Phys. Rev. C 106 014905 Google Scholar
[19]	Li H, Xia X L, Huang X G, Huang H Z 2022 Phys. Lett. B 827 136971 Google Scholar
[20]	Wu X Y, Qin G Y, Pang L G, Wang X N 2022 Phys. Rev. C 105 034909 Google Scholar
[21]	Yi C, Pu S, Yang D L 2021 Phys. Rev. C 104 064901 Google Scholar
[22]	Yi C, Pu S, Gao J H, Yang D L 2022 Phys. Rev. C 105 044911 Google Scholar
[23]	Zhang H X, Xiao Y X, Kang J W, Zhang B W 2022 Nucl. Sci. Tech. 33 150 Google Scholar
[24]	STAR Collaboration, Adamczyk L, et al. 2017 Nature 548 62 Google Scholar
[25]	STAR Collaboration, Adam J, et al. 2018 Phys. Rev. C 98 014910 Google Scholar
[26]	STAR Collaboration, Adam J, et al. 2019 Phys. Rev. Lett. 123 132301 Google Scholar
[27]	STAR Collaboration, Abdallah M S, et al. 2023 Nature 614 244 Google Scholar
[28]	Wang X N 2023 Nucl. Sci. Tech. 34 16 Google Scholar
[29]	高建华, 盛欣力, 王群, 庄鹏飞 2023 72 072501 Gao J H, Sheng X L, Wang Q, Zhuang P F 2023 Acta Phys. Sin. 72 072501
[30]	盛欣力, 梁作堂, 王群 2023 72 072502 Sheng X L, Liang Z T, Wang Q 2023 Acta Phys. Sin. 72 072502
[31]	Pang L G, Petersen H, Wang X N 2018 Phys. Rev. C 97 064918 Google Scholar
[32]	Loizides C, Kamin J, d'Enterria D 2018 Phys. Rev. C 97 054910 Google Scholar
[33]	Shen C, Schenke B 2018 Phys. Rev. C 97 024907 Google Scholar
[34]	Bialas A, Jezabek M 2004 Phys. Lett. B 590 233 Google Scholar
[35]	Akamatsu Y, Asakawa M, Hirano T, Kitazawa M, Morita K, Murase K, Nara Y, Nonaka C, Ohnishi A 2018 Phys. Rev. C 98 024909 Google Scholar
[36]	Denicol G S, Gale C, Jeon S, Monnai A, Schenke B, Shen C 2018 Phys. Rev. C 98 034916 Google Scholar
[37]	Monnai A, Schenke B, Shen C 2019 Phys. Rev. C 100 024907 Google Scholar
[38]	Monnai A, Schenke B, Shen C 2021 Int. J. Mod. Phys. A 36 2130007 Google Scholar
[39]	McNelis M, Heinz U 2021 Phys. Rev. C 103 064903 Google Scholar
[40]	PHOBOS Collaboration, Alver B, et al. 2011 Phys. Rev. C 83 024913 Google Scholar
[41]	赵新丽, 马国亮, 马余刚 2023 Accepted Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. Accepted (in Chinese)
[42]	Lan S W, Shi S S 2022 Nucl. Sci. Tech. 33 21
[43]	STAR Collaboration, Abelev B I, et al. 2008 Phys. Rev. Lett. 101 252301 Google Scholar
[44]	STAR Collaboration, Adamczyk L, et al. 2012 Phys. Rev. Lett. 108 202301 Google Scholar
[45]	Becattini F, Chandra V, Zanna L D, Grossi E 2013 Annals Phys. 338 32 Google Scholar
[46]	Fang R H, Pang L G, Wang Q, Wang X N 2016 Phys. Rev. C 94 024904 Google Scholar
[47]	Hidaka Y, Pu S, Yang D L 2018 Phys. Rev. D 97 016004 Google Scholar
[48]	Becattini F, Buzzegoli M, Palermo A 2021 Phys. Lett. B 820 136519 Google Scholar
[49]	Becattini F, Buzzegoli M, Inghirami G, Karpenko I, Palermo A 2021 Phys. Rev. Lett. 127 272302 Google Scholar
[50]	Liu S Y F, Yin Y 2021 Phys. Rev. D 104 054043 Google Scholar
[51]	Liu S Y F, Yin Y 2021 JHEP 07 188
[52]	Fu B C, Liu S Y F, Pang L G, Song H C, Yin Y 2021 Phys. Rev. Lett. 127 142301 Google Scholar
[53]	Fu B C, Pang L G, Song H C, Yin Y 2022 arXiv: 2201.12970.

施引文献

图 1 相对论重离子碰撞中核-核非对心对撞示意图, 碰撞后介质沿纵向($ \pm\hat{{\boldsymbol{z}}} $)方向不对称. QGP火球在碰撞平面(xz平面)上存在逆时针旋转的纵向倾斜

Fig. 1. Schematic figure for non-central heavy-ion collisions. Counter-clockwise tilt of the QGP fireball is created in the reaction (xz) plane

下载: 全尺寸图片幻灯片

图 2 非对心Au+Au碰撞产生的QGP的初始能量密度(上)与重子数密度(下)在反应平面内的分布. 此处展现了中心度为 20%—60% (b = 9.0 fm)下200 AGeV Au+Au 碰撞的情形. 箭头表示QGP 火球相对于纵方向的逆时针倾斜

Fig. 2. The initial energy density (up) and baryon density (down) on the $ \eta_{{\rm{s}}} $-$ x $ plane in 20%–60% (b = 9.0 fm) 200 AGeV Au+Au collisions

下载: 全尺寸图片幻灯片

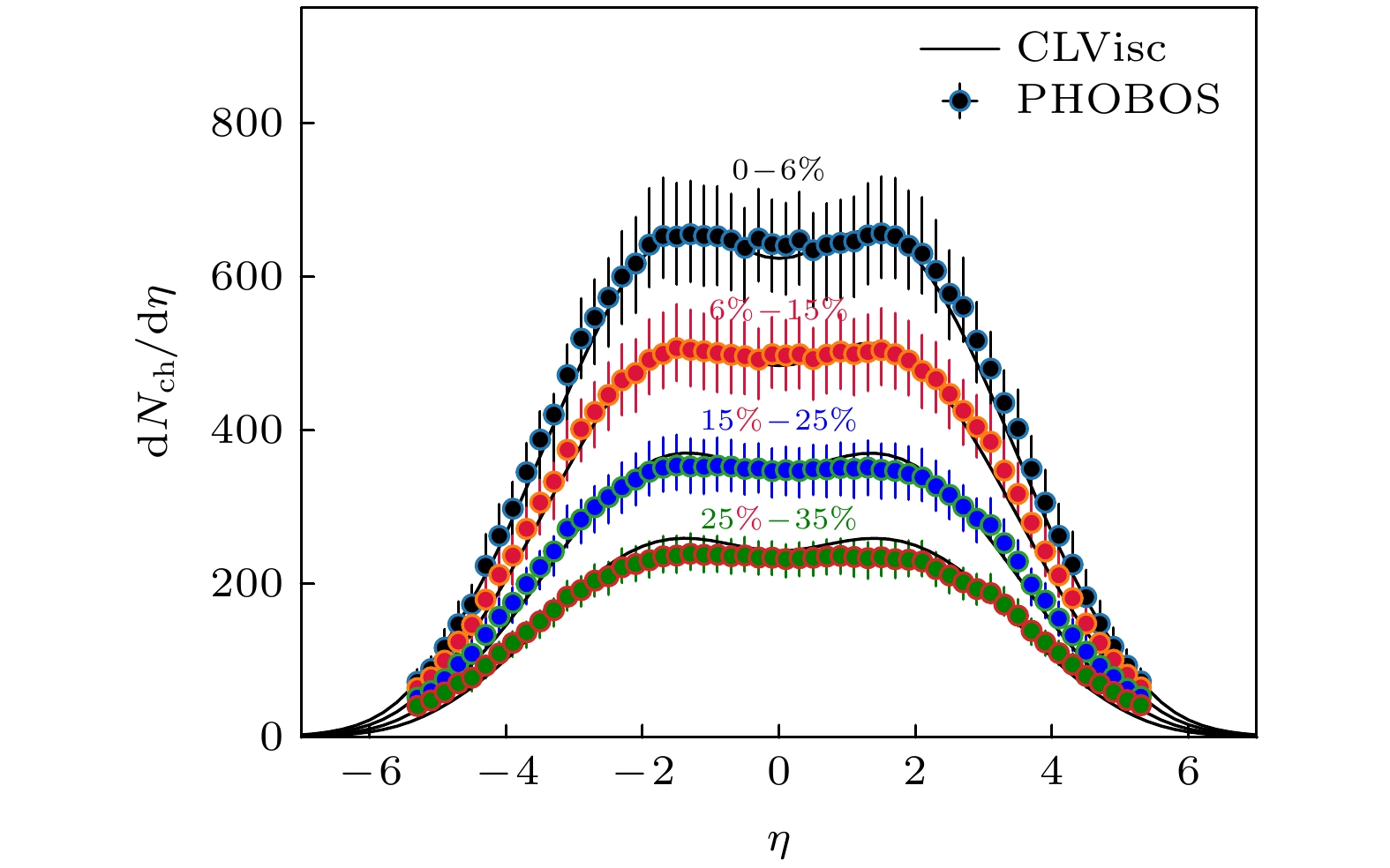
图 3 末态带电强子在200 AGeV Au+Au碰撞不同中心度的赝快度分布$ {\rm{d}}N_{{\rm{ch}}}/{\rm{d}}\eta $. 实线为理论计算结果, 实心圆点为 RHIC-PHOBOS 的测量结果^[40]

Fig. 3. Pseudorapidity distribution $ {\rm{d}}N_{{\rm{ch}}}/{\rm{d}}\eta $ of charged light hadrons in Au+Au collisions at $ \sqrt{s_{\rm{NN}}} = 200 $ GeV, compared between the CLVisc hydrodynamic calculation and the PHOBOS data^[40]

下载: 全尺寸图片幻灯片

图 4 200 AGeV Au+Au 碰撞不同中心度的直接流$ v_{1} $. 左图为带电粒子直接流对赝快度的依赖, 右图为质子及反质子直接流对快度的依赖. 实验结果取自STAR实验组^[43,44]

Fig. 4. Directed flow $ v_{1} $ of charged hadrons (left) and protons and anti-protons (right) in Au+Au collisions at $ \sqrt{s_{\rm{NN}}} = 200 $ GeV, compared between the CLVisc hydrodynamic calculation and the STAR data^[43,44]

下载: 全尺寸图片幻灯片

图 5 200 AGeV Au+Au碰撞在不同中心度的超子整体自旋极化$ P^y $. 左图为Λ超子的四种自旋极化(thermal, shear, accT, chemical)随碰撞中心度的依赖. 右图为Λ和$ \overline{\Lambda} $超子的四种自旋极化之和(total = thermal + shear + accT + chemical)随中心度的依赖. 实验数取自RHIC-STAR^[25]. 需要注意的是, 根据最新的超子衰变参数$ \alpha_{\Lambda} $, STAR合作组采集到的数据点被缩放了 0.877倍

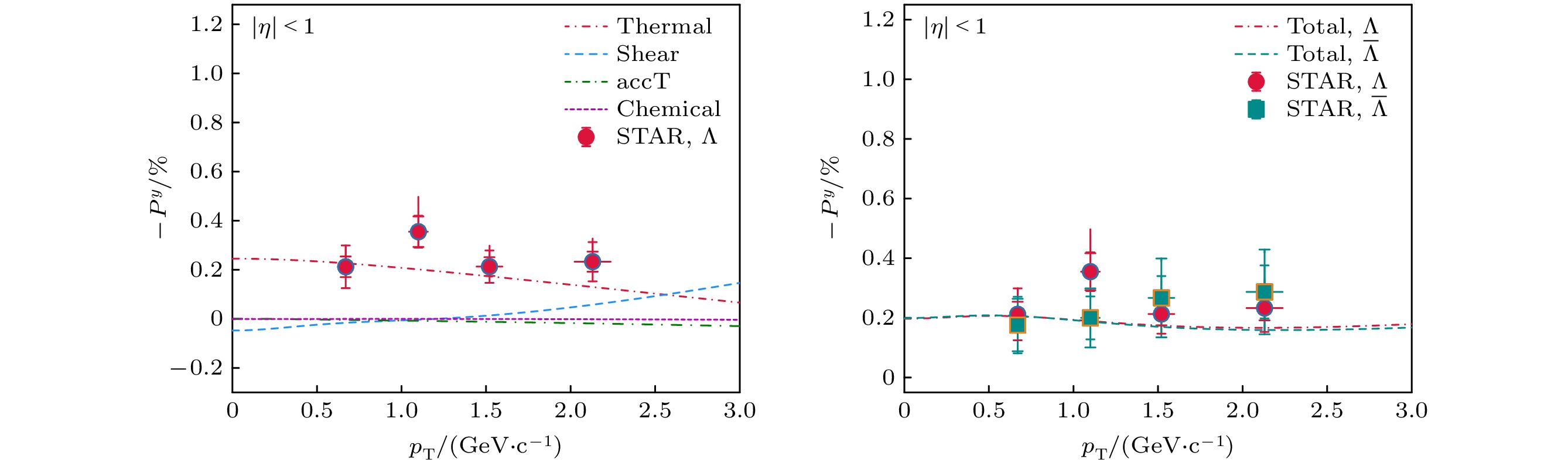
Fig. 5. Global polarization $ P^y $ of Λ and $ \bar{\Lambda} $ as a function of centrality in Au+Au collisions at $ \sqrt{s_{\rm{NN}}}=200 $ GeV, compared between the CLVisc hydrodynamic calculation and the STAR data ^[25]

下载: 全尺寸图片幻灯片

图 6 在200 AGe Au+Au碰撞中心度20%—60% 超子整体自旋极化$ P^y $对横动量$ p_{\rm{T}} $的依赖关系. 左图为 Λ超子的四种自旋极化随横动量$ p_{\rm{T}} $的依赖. 右图为Λ和$ \overline{\Lambda} $超子四种贡献之和的整体自旋极化随横动量$ p_T $的依赖. 实验数据取自RHIC-STAR^[25]

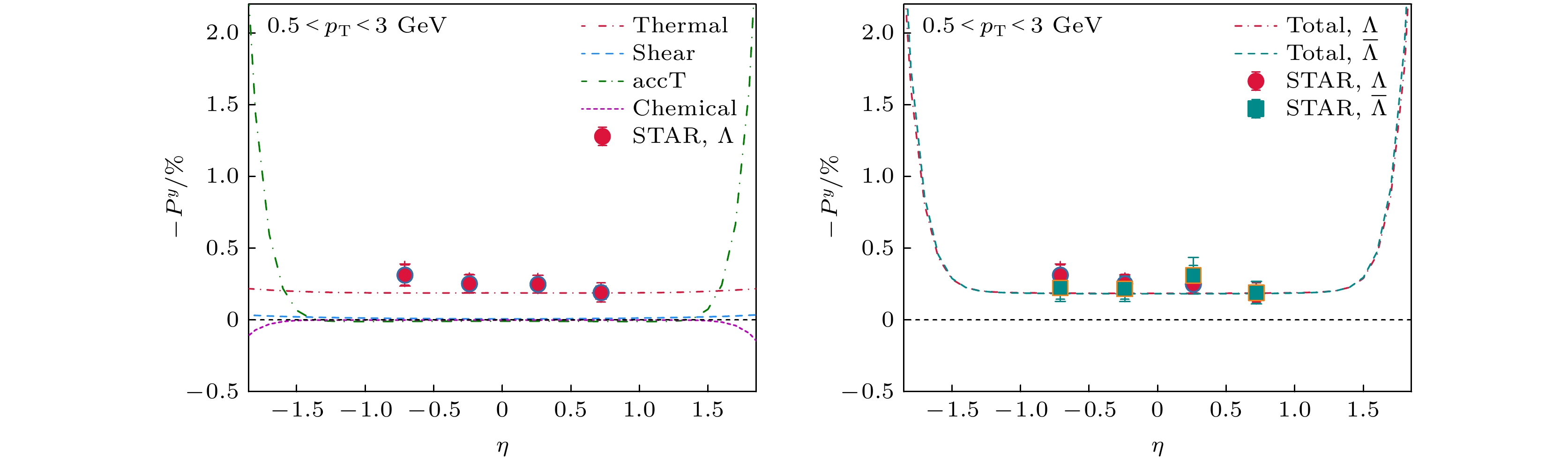
Fig. 6. Global polarization $ P^y $ of Λ and $ \bar{\Lambda} $ as a function of transverse momentum $ p_{\rm{T}} $ in 20%–60% Au+Au collisions at $ \sqrt{s_{\rm{NN}}}=200 $ GeV, compared between the CLVisc hydrodynamic calculation and the STAR data^[25]

下载: 全尺寸图片幻灯片

图 7 200 AGeV Au+Au碰撞在中心度为20%–60%的超子整体自旋极化率$ P^y $随赝快度$ \eta $的分布. 左图为Λ超子的四种自旋极化随赝快度$ \eta $ 的分布. 右图为Λ超子和$ \overline{\Lambda} $超子四种贡献之和的整体自旋极化率随赝快度的分布. 实验数据来自RHIC-STAR^[25]

Fig. 7. Global polarization $ P^y $ of Λ and $ \bar{\Lambda} $ as a function of pseudo-rapidity in Au+Au collisions at $ \sqrt{s_{\rm{NN}}}=200 $ GeV, compared between the CLVisc hydrodynamic calculation and the STAR data^[25]

下载: 全尺寸图片幻灯片

map

[1]	Bass S A, Gyulassy M, Stoecker H, Greiner W 1999 J. Phys. G 25 R1 Google Scholar
[2]	Rischke D H, Pürsün Y, Maruhn J A, Stoecker H, Greiner W 1995 Acta Phys. Hung. A 1 309 Google Scholar
[3]	Bozek P 2022 Phys. Rev. C 106 L061901 Google Scholar
[4]	Bozek P 2012 Phys. Rev. C 85 034901 Google Scholar
[5]	Jiang Z F, Cao S S, Wu X Y, Yang C B, Zhang B W 2022 Phys. Rev. C 105 034901 Google Scholar
[6]	Jiang Z F, Yang C B, Peng Q 2021 Phys. Rev. C 104 064903 Google Scholar
[7]	Shen C, Alzhrani S 2020 Phys. Rev. C 102 014909 Google Scholar
[8]	Ryu S, Jupic V, Shen C 2021 Phys. Rev. C 104 054908 Google Scholar
[9]	Wang H, Chen J H 2022 Nucl. Sci. Tech. 33 15 Google Scholar
[10]	高建华, 黄旭光, 梁作堂, 王群, 王新年 2023 72 072501 Gao J H, Huang X G, Liang Z T, Wang Q, Wang X N 2023 Acta Phys. Sin. 72 072501 (in Chinese)
[11]	Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 Google Scholar
[12]	Liang Z T, Wang X N 2005 Phys. Lett. B 629 20 Google Scholar
[13]	孙旭, 周晨升, 陈金辉, 陈震宇, 马余刚, 唐爱洪, 徐庆华 2023 72 072401 Sun X, Zhou C S, Chen J H, Chen Z Y, Ma Y G, Tang A H, Xu Q H 2023 Acta Phys. Sin. 72 072401 (in Chinese)
[14]	浦实, 黄旭光 2023 72 071202 Pu S, Huang X G 2023 Acta Phys. Sin. 72 071202 (in Chinese)
[15]	尹伊 2023 Accepted Yin Y 2023 Acta Phys. Sin. this volume Accepted (in Chinese)
[16]	Huang X G, Huovinen P, Wang X N 2011 Phys. Rev. C 84 054910 Google Scholar
[17]	Li X W, Jiang Z F, Cao S S, Deng J 2023 Eur. Phys. J. C 83 96 Google Scholar
[18]	Alzhrani S, Ryu S, Shen C 2022 Phys. Rev. C 106 014905 Google Scholar
[19]	Li H, Xia X L, Huang X G, Huang H Z 2022 Phys. Lett. B 827 136971 Google Scholar
[20]	Wu X Y, Qin G Y, Pang L G, Wang X N 2022 Phys. Rev. C 105 034909 Google Scholar
[21]	Yi C, Pu S, Yang D L 2021 Phys. Rev. C 104 064901 Google Scholar
[22]	Yi C, Pu S, Gao J H, Yang D L 2022 Phys. Rev. C 105 044911 Google Scholar
[23]	Zhang H X, Xiao Y X, Kang J W, Zhang B W 2022 Nucl. Sci. Tech. 33 150 Google Scholar
[24]	STAR Collaboration, Adamczyk L, et al. 2017 Nature 548 62 Google Scholar
[25]	STAR Collaboration, Adam J, et al. 2018 Phys. Rev. C 98 014910 Google Scholar
[26]	STAR Collaboration, Adam J, et al. 2019 Phys. Rev. Lett. 123 132301 Google Scholar
[27]	STAR Collaboration, Abdallah M S, et al. 2023 Nature 614 244 Google Scholar
[28]	Wang X N 2023 Nucl. Sci. Tech. 34 16 Google Scholar
[29]	高建华, 盛欣力, 王群, 庄鹏飞 2023 72 072501 Gao J H, Sheng X L, Wang Q, Zhuang P F 2023 Acta Phys. Sin. 72 072501
[30]	盛欣力, 梁作堂, 王群 2023 72 072502 Sheng X L, Liang Z T, Wang Q 2023 Acta Phys. Sin. 72 072502
[31]	Pang L G, Petersen H, Wang X N 2018 Phys. Rev. C 97 064918 Google Scholar
[32]	Loizides C, Kamin J, d'Enterria D 2018 Phys. Rev. C 97 054910 Google Scholar
[33]	Shen C, Schenke B 2018 Phys. Rev. C 97 024907 Google Scholar
[34]	Bialas A, Jezabek M 2004 Phys. Lett. B 590 233 Google Scholar
[35]	Akamatsu Y, Asakawa M, Hirano T, Kitazawa M, Morita K, Murase K, Nara Y, Nonaka C, Ohnishi A 2018 Phys. Rev. C 98 024909 Google Scholar
[36]	Denicol G S, Gale C, Jeon S, Monnai A, Schenke B, Shen C 2018 Phys. Rev. C 98 034916 Google Scholar
[37]	Monnai A, Schenke B, Shen C 2019 Phys. Rev. C 100 024907 Google Scholar
[38]	Monnai A, Schenke B, Shen C 2021 Int. J. Mod. Phys. A 36 2130007 Google Scholar
[39]	McNelis M, Heinz U 2021 Phys. Rev. C 103 064903 Google Scholar
[40]	PHOBOS Collaboration, Alver B, et al. 2011 Phys. Rev. C 83 024913 Google Scholar
[41]	赵新丽, 马国亮, 马余刚 2023 Accepted Zhao X L, Ma G L, Ma Y G 2023 Acta Phys. Sin. Accepted (in Chinese)
[42]	Lan S W, Shi S S 2022 Nucl. Sci. Tech. 33 21
[43]	STAR Collaboration, Abelev B I, et al. 2008 Phys. Rev. Lett. 101 252301 Google Scholar
[44]	STAR Collaboration, Adamczyk L, et al. 2012 Phys. Rev. Lett. 108 202301 Google Scholar
[45]	Becattini F, Chandra V, Zanna L D, Grossi E 2013 Annals Phys. 338 32 Google Scholar
[46]	Fang R H, Pang L G, Wang Q, Wang X N 2016 Phys. Rev. C 94 024904 Google Scholar
[47]	Hidaka Y, Pu S, Yang D L 2018 Phys. Rev. D 97 016004 Google Scholar
[48]	Becattini F, Buzzegoli M, Palermo A 2021 Phys. Lett. B 820 136519 Google Scholar
[49]	Becattini F, Buzzegoli M, Inghirami G, Karpenko I, Palermo A 2021 Phys. Rev. Lett. 127 272302 Google Scholar
[50]	Liu S Y F, Yin Y 2021 Phys. Rev. D 104 054043 Google Scholar
[51]	Liu S Y F, Yin Y 2021 JHEP 07 188
[52]	Fu B C, Liu S Y F, Pang L G, Song H C, Yin Y 2021 Phys. Rev. Lett. 127 142301 Google Scholar
[53]	Fu B C, Pang L G, Song H C, Yin Y 2022 arXiv: 2201.12970.

[1]	孙旭, 周晨升, 陈金辉, 陈震宇, 马余刚, 唐爱洪, 徐庆华. 重离子碰撞中QCD物质整体极化的实验测量. , 2023, 72(7): 072401. doi: 10.7498/aps.72.20222452
[2]	高建华, 盛欣力, 王群, 庄鹏飞. 费米子的相对论自旋输运理论. , 2023, 72(11): 112501. doi: 10.7498/aps.72.20222470
[3]	阮丽娟, 许长补, 杨驰. 夸克物质中的超子整体极化与矢量介子自旋排列. , 2023, 72(11): 112401. doi: 10.7498/aps.72.20230496
[4]	寿齐烨, 赵杰, 徐浩洁, 李威, 王钢, 唐爱洪, 王福强. 相对论重离子碰撞中的手征效应实验研究. , 2023, 72(11): 112504. doi: 10.7498/aps.72.20230109
[5]	浦实, 黄旭光. 相对论自旋流体力学. , 2023, 72(7): 071202. doi: 10.7498/aps.72.20230036
[6]	高建华, 黄旭光, 梁作堂, 王群, 王新年. 强相互作用自旋-轨道耦合与夸克-胶子等离子体整体极化. , 2023, 72(7): 072501. doi: 10.7498/aps.72.20230102
[7]	刘鹤, 初鹏程. 相对论重离子碰撞中π介子椭圆流劈裂. , 2023, 72(13): 132101. doi: 10.7498/aps.72.20230454
[8]	张善良, 邢宏喜, 王恩科. 相对论重离子碰撞中的喷注淬火效应. , 2023, 72(20): 200304. doi: 10.7498/aps.72.20230993
[9]	杨帅, 唐泽波, 杨驰, 查王妹. 相对论重离子碰撞中光子-光子相互作用的碰撞参数依赖性. , 2023, 72(20): 201201. doi: 10.7498/aps.72.20230948
[10]	张晓辉, 董克攻, 华剑飞, 朱斌, 谭放, 吴玉迟, 鲁巍, 谷渝秋. 相对论皮秒激光在低密度等离子体中直接加速的电子束的横向分布特征研究. , 2019, 68(19): 195203. doi: 10.7498/aps.68.20191106
[11]	管娜娜. 胶子非弹性散射过程对夸克胶子等离子体中双轻子产生的影响. , 2016, 65(14): 142501. doi: 10.7498/aps.65.142501
[12]	陈小凡. 相对论重离子碰撞中部分相干源的相干因子. , 2012, 61(9): 092501. doi: 10.7498/aps.61.092501
[13]	罗牧华, 张秋菊, 闫春燕. 超相对论激光和稠密等离子体作用产生阿秒脉冲的优化. , 2010, 59(12): 8559-8565. doi: 10.7498/aps.59.8559
[14]	刘炯, 袁业飞, 邓小龙. 等离子体中相对论电子的同步曲率辐射特性研究. , 2007, 56(2): 1214-1223. doi: 10.7498/aps.56.1214
[15]	徐慧, 盛政明, 张杰. 相对论效应对激光在等离子体中的共振吸收的影响. , 2006, 55(10): 5354-5361. doi: 10.7498/aps.55.5354
[16]	段文山, 洪学仁. 弱相对论等离子体横向扰动下的离子声孤波. , 2003, 52(6): 1337-1339. doi: 10.7498/aps.52.1337
[17]	贺泽君, 蒋维渊, 朱志远, 刘波. 夸克-胶子等离子体在相对论性核-核碰撞中形成的一种信号. , 2000, 49(5): 911-914. doi: 10.7498/aps.49.911
[18]	屈一至, 仝晓民, 李家明. 电子与原子、离子碰撞过程的相对论效应. , 1995, 44(11): 1719-1726. doi: 10.7498/aps.44.1719
[19]	郭世宠, 蔡诗东. 任意磁场位形下弱相对论等离子体的普遍色散关系. , 1987, 36(7): 870-880. doi: 10.7498/aps.36.870
[20]	何祚庥, 林大航, 赵培贞. 考虑胶子质量的重夸克偶素位模型. , 1982, 31(4): 525-531. doi: 10.7498/aps.31.525

计量

文章访问数: 5401
PDF下载量: 195
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

RHIC能区Au+Au 碰撞中带电粒子直接流与超子整体极化的计算与分析