-
玻色-爱因斯坦凝聚中由于非线性相互作用引起的涡旋激发态一直是超冷原子研究的热点. 然而相关研究都集中在具有整数拓扑荷的正则涡旋态. 本文研究了具有幂指数、新型幂指数和振荡型三种相位分布的非正则涡旋光与凝聚体相互作用而产生的非正则涡旋态凝聚体的动力学性质. 研究表明非正则涡旋具有动力学不稳定性, 其密度分布显著依赖于光场相位结构参数. 不同非正则涡旋衰变形成具有不同分布的正则涡旋簇, 展现出丰富的动力学激发斑图. 特别是新型幂指数非正则涡旋态衰变后会在凝聚体内形成稳定的正多边形正则涡旋簇结构. 由于非正则涡旋光的相位结构破坏了凝聚体的旋转对称性, 凝聚体的角动量不再是量子化的, 且其随光场方位角幂次或振荡频率的变化与相应的非正则涡旋光场自身演化具有明显差别. 在动力学演化过程中, 具有新型幂指数相位的非正则涡旋态凝聚体质心保持不变, 而对于具有幂指数和振荡型相位的非正则涡旋态凝聚体, 两者的质心轨迹是一个中心为坐标原点的非标准椭圆.Vortex excitations triggered by nonlinear interactions in Bose-Einstein condensates have attracted interest in the study of ultracold atoms. However, most studies focus on canonical vortex states with integer topological charges. In this paper, we study the dynamic properties of noncanonical vortex condensates with three phase distributions: power-exponent, new type power-exponent and oscillation type. The results show that the noncanonical vortices are dynamic unstable and their density distributions obviously depend on the phase parameters of the initial optical phase masks. Different noncanonical vortices decay into canonical clusters with diverse configurations showing rich topological excitation patterns. In particular, a new power exponential noncanonical vortex state decays into a stable canonical polygonal vortex cluster structure. Because the phase structures of the noncanonical optical vortices destroy the rotational symmetry of the condensate, the angular momentum of the condensate is no longer quantized, and its value changes with the power of the azimuthal angle of the optical field or the oscillation frequency, which is obviously different from the evolution of the corresponding noncanonical vortex optical field itself. In the dynamical process, the center-of-mass trajectory of noncanonical vortex condensates with the new type of power exponent phase is always a point, while for the noncanonical vortex condensates with power exponent and oscillating phase, the center-of-mass trajectories are ellipses centering at the origin of coordinates.
-
Keywords:
- Bose-Einstein condensate /
- noncanonical vortex states /
- canonical vortex cluster /
- angular momentum /
- center-of-mass trajectories
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] O'Neil A T, MacVicar I, Allen L, Padgett M J 2002 Phys. Rev. Lett. 88 053601
Google Scholar
[3] Molina-Terriza G, Torres J P, Torner L 2007 Nat. Phys. 3 305
Google Scholar
[4] Ng J, Lin Z F, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[5] Fan C J, Liu Y X, Wang X Y, Chen Z Y, Pu J X 2018 JOSAA 35 903
Google Scholar
[6] Grier D G 2003 Nature 424 810
Google Scholar
[7] Li P, Liu S, Peng T, Xie G F, Gan X T, Zhao J L 2014 Opt. Express 22 7598
Google Scholar
[8] Shen D H, Wang K, Zhao D M 2019 Opt. Express 27 24642
Google Scholar
[9] Barrett M D, Sauer J A, Chapman M S 2001 Phys. Rev. Lett. 87 010404
Google Scholar
[10] Du R, Xing J C, Xiong Bo, Zheng J H, Yang T 2022 Chin. Phys. Lett. 39 070304
Google Scholar
[11] Burger S, Cataliotti F S, Fort C, Minardi F, Inguscio M, Chiofalo M L, Tosi M P 2001 Phys. Rev. Lett. 86 4447
Google Scholar
[12] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y J, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[13] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen Shuai, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[14] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[15] Wang Z Y, Cheng X C, Wang B Z, et al. 2021 Science 372 271
Google Scholar
[16] Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[17] Cheng Q L, Bai W K, Zhang Y Z, Xiong B, Yang T 2018 Laser Phys. 29 015501
Google Scholar
[18] Wang D M, Xing J C, Du R, Xiong B, Yang T 2021 Chin. Phys. B 30 120303
Google Scholar
[19] Martin A M, Scott R G, Fromhold T M 2007 Phys. Rev. A 75 065602
Google Scholar
[20] Gauthier G, Reeves M T, Yu X Q, Bradley A S, Baker M A, Bell T A, Rubinsztein-Dunlop H, Davis M J, Neely T W 2019 Science 364 1264
Google Scholar
[21] Madison K W, Chevy F, Wohlleben W, Dalibard J 2000 Phys. Rev. Lett. 84 806
Google Scholar
[22] Wright K C, Blakestad R B, Lobb C J, Phillips W D, Campbell G K 2013 Phys. Rev. Lett. 110 025302
Google Scholar
[23] Chen X Y, Yang T, Yang W L, Liu W M 2020 arXiv: 2007.02274 [cond-mat.quant-gas]
[24] Theis M, Thalhammer G, Winkler K, Hellwig M, Ruff G, Grimm R, Denschlag J H 2004 Phys. Rev. Lett. 93 123001
Google Scholar
[25] Denschlag J, Simsarian J E, Feder D L, Clark C W, Collins L A, Cubizolles J, Deng L, Hagley E W, Helmerson K, Reinhardt W P, Rolston S L, Schneider B I, Phillips W D 2000 Science 287 97
Google Scholar
[26] Crasovan L C, Vekslerchik V, Pérez-García V M, Torres J P, Mihalache D, Torner L 2003 Phys. Rev. A 68 063609
Google Scholar
[27] Möttönen M, Virtanen S M M, Isoshima T, Salomaa M M 2005 Phys. Rev. A 71 033626
Google Scholar
[28] Yang T, Hu Z Q, Zou S, Liu W M 2016 Scientific Reports 6 1
Google Scholar
[29] Coddington I, Engels P, Schweikhard V, Cornell E A 2003 Phys. Rev. Lett. 91 100402
Google Scholar
[30] Tsubota M, Kasamatsu K, Ueda M 2002 Phys. Rev. A 65 023603
Google Scholar
[31] Xiong B, Yang T, Lin Y J, Wang D W 2020 J. Phys. B: Atom. Mol. Opt. Phys. 53 075301
Google Scholar
[32] Yang T, Xiong B, Benedict K A 2013 Phys. Rev. A 87 023603
Google Scholar
[33] Xiong B, Yang T, Benedict K A 2013 Phys. Rev. A 88 043602
Google Scholar
[34] Bai W K, Yang T, Liu W M 2020 Phys. Rev. A 102 063318
Google Scholar
[35] Bai W K, Xing J C, Yang T, Yang W L, Liu W M 2021 Results Phys. 22 103828
Google Scholar
[36] Zou S, Bai W K, Yang T, Liu W M 2021 Phys. Fluids 33 027105
Google Scholar
[37] Scherer D R, Weiler C N, Neely T W, Anderson B P 2007 Phys. Rev. Lett. 98 110402
Google Scholar
[38] Ruben Gary, Paganin D M, Morgan M J 2008 Phys. Rev. A 78 013631
Google Scholar
[39] Yang T, Henning A J, Benedict K A 2014 Laser Phys. 24 115502
Google Scholar
[40] Liu W M, Wu B, Niu Q 2000 Phys. Rev. Lett. 84 2294
Google Scholar
[41] Feder D L, Clark C W, Schneider B I 1999 Phys. Rev. A 61 011601
Google Scholar
-
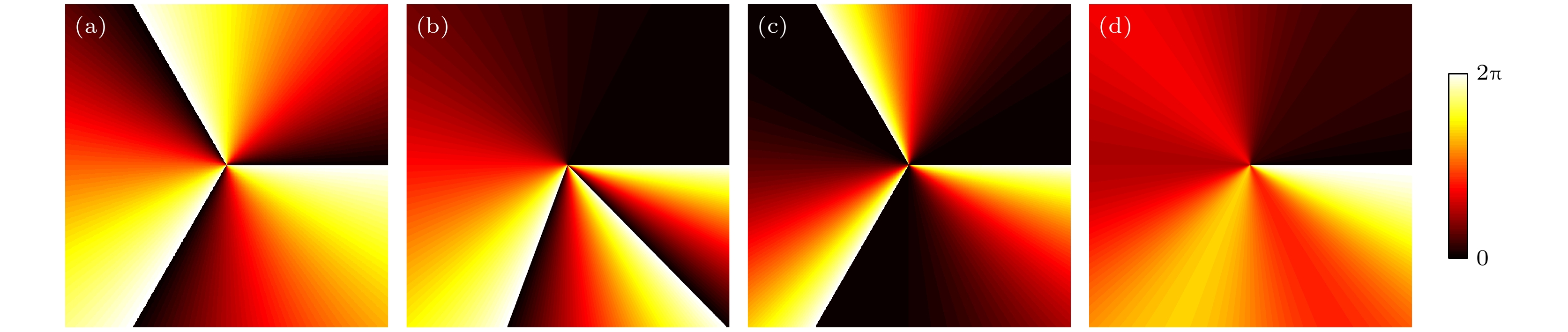
图 1 涡旋场相位空间分布图 (a) 拓扑荷
$ m=3 $ 的正则涡旋场相位分布; (b) 拓扑荷和幂次分别为$m=3, n=3$ 的PEPV型涡旋场相位分布; (c) 拓扑荷和幂次分别为$m=3, n=3$ 的NPEPV型涡旋场相位分布; (d) 拓扑荷和角频率分别为$m=1, $ $ \omega=3$ 的OSCPV型涡旋场相位分布Fig. 1. Phase distributions of vortex fields: (a) Phase distribution of the canonical vortex with topological charge
$m=3$ ; (b) phase distribution of PEPV vortex with the topological charge and power being$m=3$ and$n=3$ , respectively; (c) phase distribution of NPEPV vortex with the topological charge and power being$m=3$ and$n=3$ , respectively; (d) phase distribution of OSCPV vortex with topological charge and angular frequency being$m=1$ and$\omega=3$ , respectively.
图 2 通过相位印记获得的非正则涡旋态凝聚体密度分布 PEPV态: (a)—(c)分别对应拓扑荷
$m=1, 3, 5$ ; I和II行分别对应幂次$n=5$ 和$n=10$ . NPEPV态: (d)—(f)分别对应拓扑荷$m=3, 4, 5$ ; I和II行分别对应幂次$n=5$ 和$n=10$ . OSCPV态: (g)—(i)分别对应拓扑荷$m=1, 3, 5$ ; I和II行分别对应角频率$\omega=5$ 和$\omega=10$ Fig. 2. Density distributions of the condensates in noncanonical vortex states. PEPV states: (a)–(c) Density distributions with the topological charge
$m=1, 3, 5$ , respectively. In row I and II, the powers are$n=5$ and$10$ , respectively. NPEPV states: (d)–(f) Density distributions with the topological charge$m=3, 4, 5$ , respectively. In row I and II, the powers are$n=5$ and$10$ , respectively. OSCPV state: (g)–(i) Density distributions with the topological charge$m=1, 3, 5$ , respectively. In row I and II, the angular frequencies are$\omega=5$ and$10$ , respectively.
图 3 拓扑荷
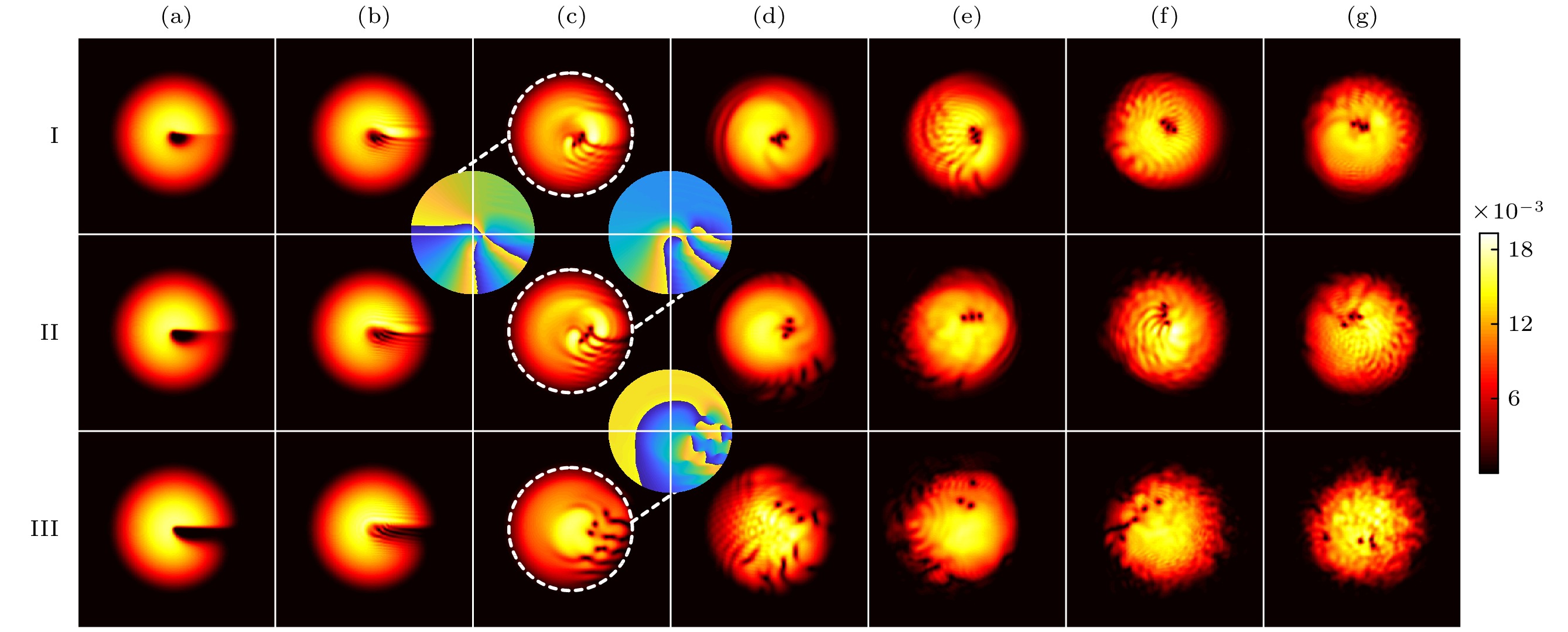
$ m=3 $ 的PEPV型非正则涡旋态凝聚体的动力学演化, 其中 I到III行分别对应幂次$n=3, 5, 10$ I(a)—I(g) 分别对应时间$t/t_0=0, 0.1, 0.4, 1.5, 3.5, 6.5, 9.5$ ; II(a)—II(g) 分别对应时间$t/t_0=0, 0.1, 0.5, 2.5, 5.5, 8.5, 10$ ; III(a)—III(g) 分别对应时间$t/t_0=0, 0.1, 0.9, 3.5, 6.0, 9.5, 14.5$ . 其中子图表示与白色虚线包围部分凝聚体密度分布对应的相位分布Fig. 3. Dynamic evolution of condensates in PEPV state, where the topological charge is
$m=3$ , and the corresponding powers from row I to row III are$n=3, 5, 10$ , respectively: I(a)–I(g) Times are$t/t_0=0, 0.1, 0.4, 1.5, 3.5, 6.5, 9.5$ ; II(a)–II(g) times are$t/t_0= 0, 0.1, 0.5, 2.5, 5.5, 8.5, 10 $ ; III(a)–III(g) times are$t/t_0= 0, 0.1, 0.9, 3.5, 6.0, 9.5, 14.5$ . Here, the subgraphs represent the corresponding phase distributions of the density distributions surrounded by the white dashed circles.
图 4 NPEPV型非正则涡态凝聚体的动力学演化 (a)—(f)拓扑荷
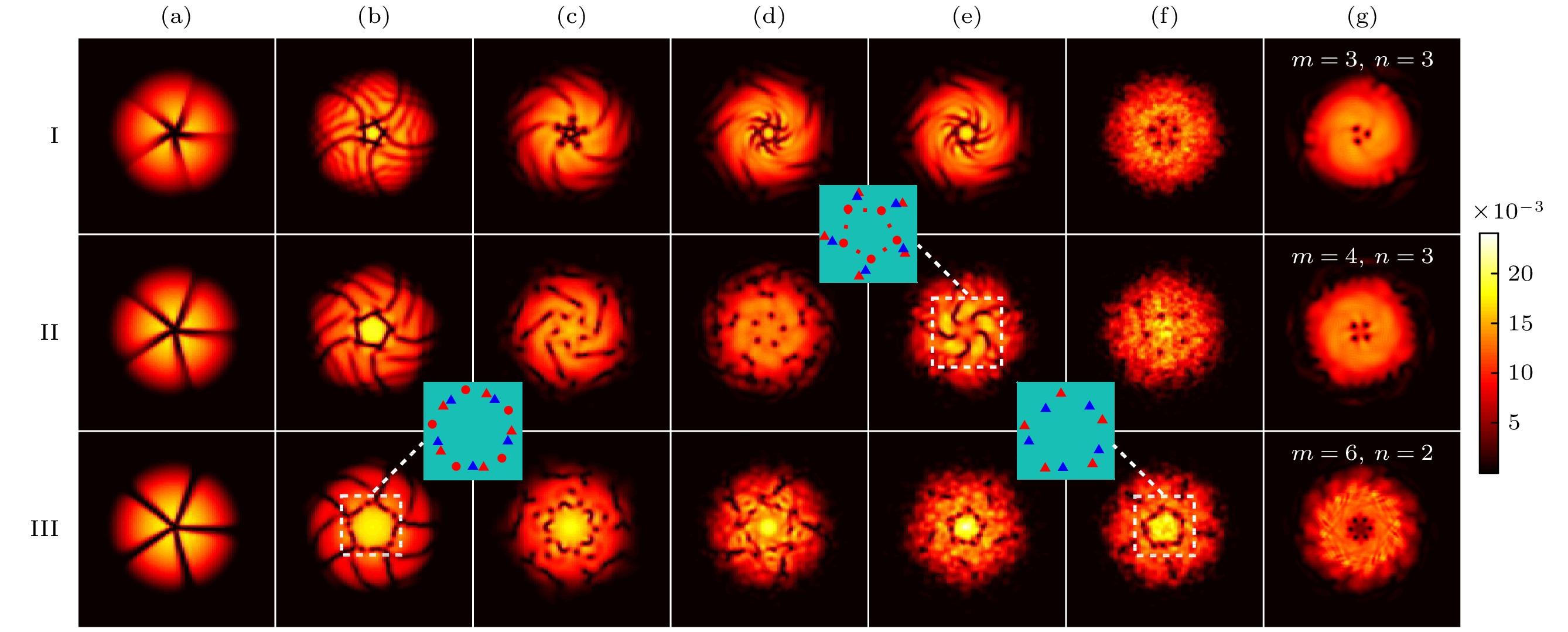
$ m=5$ , I到III行分别对应幂次$ n=3, 5, 10$ ; I(a)—I(f) 分别对应时间$ t/t_0=0, 0.55, 1.25, 1.55, 1.65, 16$ ; II(a)—II(f)分别对应时间$t/t_0=0, 0.85, 1.8, 2.5, 5, 16$ ; III(a)—III(f)分别对应时间$ t/t_0=0, 1.1, 1.8, 4.95, 8.2, 8.9$ ; I(g)—III(g)分别对应时间$t/t_0=2.5, 2.5, 3.1$ . 其中子图表示涡旋核的位置, 圆点表示非正则涡旋衰变形成的正则涡旋核, 三角表示干涉形成的涡旋对. 红色表示涡旋荷为正, 蓝色表示涡旋荷为负Fig. 4. Dynamic evolution of condensates in NPEPV states. The topological charge in (a)–(f) is
$m=5$ , the powers from row I to row III are$n=3, 5, 10 $ , respectively: I(a)–I(f) Time are$t/t_0=0, 0.55, 1.25, 1.55, 1.65, 16 $ , respectively; II(a)–II(f) times are$t/t_0=0, 0.85, 1.8, 2.5, 5, 16$ , respectively; III(a)–III(f) times are$t/t_0=0, 1.1, 1.8, 4.95, 8.2, 8.9$ , respectively; I(g)–III(g) times are$t/t_0=2.5, 2.5, 3.1$ , respectively. The subgraphs show the positions of the vortex cores. The solid dots represent the canonical vortices evolved from the decay of NPEPVs. The solid triangles represent vortex pairs evolved from the interference of condensates. The vortices with positive and negative topological charge are labeled in red and blue color, respectively.
图 5 拓扑荷为
$m=5$ 的OSCPV型非正则涡旋态凝聚体的动力学演化, 其中I—III行分别对应角频率$\omega=3, 5, 10$ I(a)—I(g)分别对应时间$ t/t_0=0, 1, 9.2, 16.2, 25.8, 35.75, 45.65$ ; II(a)—II(g)分别对应时间$ t/t_0=0, 1, 20, 25.1, 36.5, 47.6, 50$ ; III(a)—III(g)分别对应时间$ t/t_0=0, 1, 4, 11, 26.5, 36.5, 45.5$ . II—III之间的子图表示与白色虚线包围部分凝聚体密度分布对应的相位分布Fig. 5. Dynamic evolution of condensates in OSCPV states with topological charge
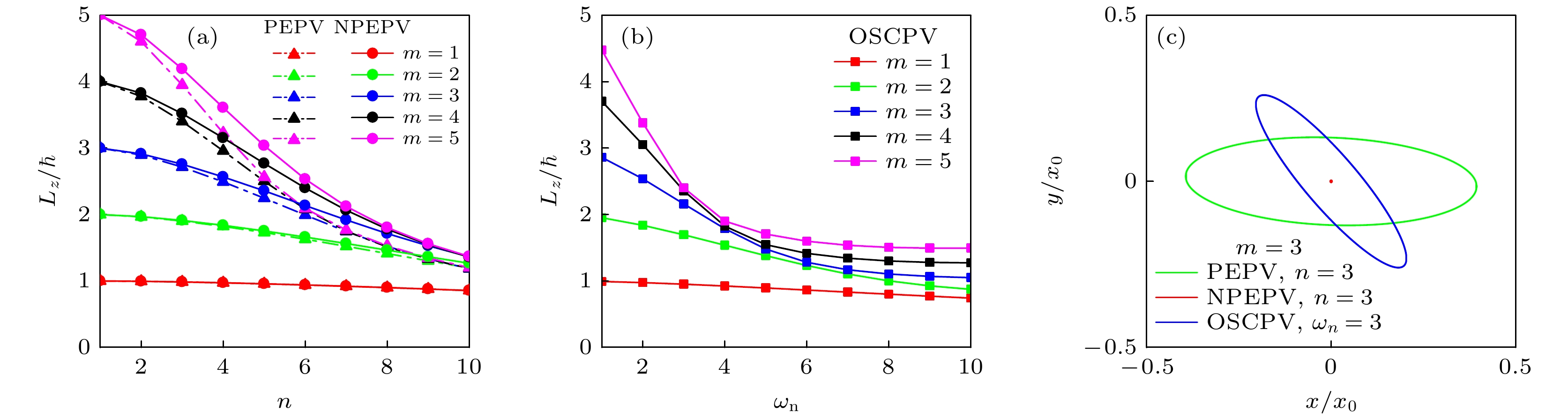
$m=5$ . The angular frequencies from row I to row III are$\omega=3, 5, 10$ , respectively: I(a)–I(g) times are$t/t_0=0, 0.35, 2.6, 10.38, 10.92, 12.02, 12.84$ , respectively; II(a)–II(g) times are$t/t_0=0, 0.3, 7.56, 10.14, 11.7, 12.7, 14.26$ , respectively; III(a)–III(g) times are$t/t_0=0, 0.4, 9.48, 12.04, 15.82, 18.42, $ $ 19.5$ , respectively. The subgraphs between row II and III represent the corresponding phase distributions of the density distributions surrounded by the white dashed circles.
图 6 凝聚体的轴向角动量与非正则涡旋幂次及角频率的关系, 以及非正则涡旋的质心轨迹. (a) 实心三角和实心圆点分别代表PEPV和NPEPV型非正则涡旋的轴向角动量; (b) OSCPV型非正则涡旋的轴向角动量; (c) 凝聚体的质心轨迹
Fig. 6. The axial angular momenta of condensates v.s. the power or the frequency of the noncanonical vortices, and the trajectories of the center of mass of the condensates with noncanonical vortices: (a) The solid triangles and the solid dots represent the axial angular momenta of condensates in PEPV and NPEPV states, respectively; (b) the axial angular momentum of condensates in OSCPV states, respectively; (c) the trajectory of the center-of-mass of the condensate.
图 7 非正则涡旋态凝聚体质心轨迹特征量随相位参数变化情况 (a)—(c) PEPV态凝聚体椭圆质心轨迹的长轴
$ a$ , 面积$ S $ 和长轴与$ x$ - 轴正方向的夹角$ \alpha $ 随相位场幂次$ n $ 变化的曲线； (d)—(f) OSCPV态凝聚体椭圆质心轨迹的长轴$ a$ , 面积$ S $ 和长轴与$ x$ -轴正方向的夹角$ \alpha $ 随相位场角频率$\omega$ 的变化Fig. 7. The relations between the characteristic parameters of the center of mass trajectories of the condensates in noncanonical vortex states and the corresponding phase field parameters: (a)–(c) The curves of the length of major axis
$a$ , the area$S$ , the angle$\alpha$ between the major axis and the positive direction of the$x$ -axis v.s. the power of the corresponding PEPV phase fields, respectively; (d)–(f) the curves of the length of major axis$a$ , the area$S$ , the angle$\alpha$ between the major axis and the positive direction of the$x$ -axis v.s. the corresponding OSCPV phase fields, respectively. -
[1] Allen L, Beijersbergen M W, Spreeuw R J C, Woerdman J P 1992 Phys. Rev. A 45 8185
Google Scholar
[2] O'Neil A T, MacVicar I, Allen L, Padgett M J 2002 Phys. Rev. Lett. 88 053601
Google Scholar
[3] Molina-Terriza G, Torres J P, Torner L 2007 Nat. Phys. 3 305
Google Scholar
[4] Ng J, Lin Z F, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[5] Fan C J, Liu Y X, Wang X Y, Chen Z Y, Pu J X 2018 JOSAA 35 903
Google Scholar
[6] Grier D G 2003 Nature 424 810
Google Scholar
[7] Li P, Liu S, Peng T, Xie G F, Gan X T, Zhao J L 2014 Opt. Express 22 7598
Google Scholar
[8] Shen D H, Wang K, Zhao D M 2019 Opt. Express 27 24642
Google Scholar
[9] Barrett M D, Sauer J A, Chapman M S 2001 Phys. Rev. Lett. 87 010404
Google Scholar
[10] Du R, Xing J C, Xiong Bo, Zheng J H, Yang T 2022 Chin. Phys. Lett. 39 070304
Google Scholar
[11] Burger S, Cataliotti F S, Fort C, Minardi F, Inguscio M, Chiofalo M L, Tosi M P 2001 Phys. Rev. Lett. 86 4447
Google Scholar
[12] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y J, Chen S, Liu X J, Pan J W 2016 Science 354 83
Google Scholar
[13] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen Shuai, Pan J W 2012 Phys. Rev. Lett. 109 115301
Google Scholar
[14] Wang P J, Yu Z Q, Fu Z K, Miao J, Huang L H, Chai S J, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301
Google Scholar
[15] Wang Z Y, Cheng X C, Wang B Z, et al. 2021 Science 372 271
Google Scholar
[16] Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[17] Cheng Q L, Bai W K, Zhang Y Z, Xiong B, Yang T 2018 Laser Phys. 29 015501
Google Scholar
[18] Wang D M, Xing J C, Du R, Xiong B, Yang T 2021 Chin. Phys. B 30 120303
Google Scholar
[19] Martin A M, Scott R G, Fromhold T M 2007 Phys. Rev. A 75 065602
Google Scholar
[20] Gauthier G, Reeves M T, Yu X Q, Bradley A S, Baker M A, Bell T A, Rubinsztein-Dunlop H, Davis M J, Neely T W 2019 Science 364 1264
Google Scholar
[21] Madison K W, Chevy F, Wohlleben W, Dalibard J 2000 Phys. Rev. Lett. 84 806
Google Scholar
[22] Wright K C, Blakestad R B, Lobb C J, Phillips W D, Campbell G K 2013 Phys. Rev. Lett. 110 025302
Google Scholar
[23] Chen X Y, Yang T, Yang W L, Liu W M 2020 arXiv: 2007.02274 [cond-mat.quant-gas]
[24] Theis M, Thalhammer G, Winkler K, Hellwig M, Ruff G, Grimm R, Denschlag J H 2004 Phys. Rev. Lett. 93 123001
Google Scholar
[25] Denschlag J, Simsarian J E, Feder D L, Clark C W, Collins L A, Cubizolles J, Deng L, Hagley E W, Helmerson K, Reinhardt W P, Rolston S L, Schneider B I, Phillips W D 2000 Science 287 97
Google Scholar
[26] Crasovan L C, Vekslerchik V, Pérez-García V M, Torres J P, Mihalache D, Torner L 2003 Phys. Rev. A 68 063609
Google Scholar
[27] Möttönen M, Virtanen S M M, Isoshima T, Salomaa M M 2005 Phys. Rev. A 71 033626
Google Scholar
[28] Yang T, Hu Z Q, Zou S, Liu W M 2016 Scientific Reports 6 1
Google Scholar
[29] Coddington I, Engels P, Schweikhard V, Cornell E A 2003 Phys. Rev. Lett. 91 100402
Google Scholar
[30] Tsubota M, Kasamatsu K, Ueda M 2002 Phys. Rev. A 65 023603
Google Scholar
[31] Xiong B, Yang T, Lin Y J, Wang D W 2020 J. Phys. B: Atom. Mol. Opt. Phys. 53 075301
Google Scholar
[32] Yang T, Xiong B, Benedict K A 2013 Phys. Rev. A 87 023603
Google Scholar
[33] Xiong B, Yang T, Benedict K A 2013 Phys. Rev. A 88 043602
Google Scholar
[34] Bai W K, Yang T, Liu W M 2020 Phys. Rev. A 102 063318
Google Scholar
[35] Bai W K, Xing J C, Yang T, Yang W L, Liu W M 2021 Results Phys. 22 103828
Google Scholar
[36] Zou S, Bai W K, Yang T, Liu W M 2021 Phys. Fluids 33 027105
Google Scholar
[37] Scherer D R, Weiler C N, Neely T W, Anderson B P 2007 Phys. Rev. Lett. 98 110402
Google Scholar
[38] Ruben Gary, Paganin D M, Morgan M J 2008 Phys. Rev. A 78 013631
Google Scholar
[39] Yang T, Henning A J, Benedict K A 2014 Laser Phys. 24 115502
Google Scholar
[40] Liu W M, Wu B, Niu Q 2000 Phys. Rev. Lett. 84 2294
Google Scholar
[41] Feder D L, Clark C W, Schneider B I 1999 Phys. Rev. A 61 011601
Google Scholar
下载:
计量
- 文章访问数: 3855
- PDF下载量: 116
- 被引次数: 0
