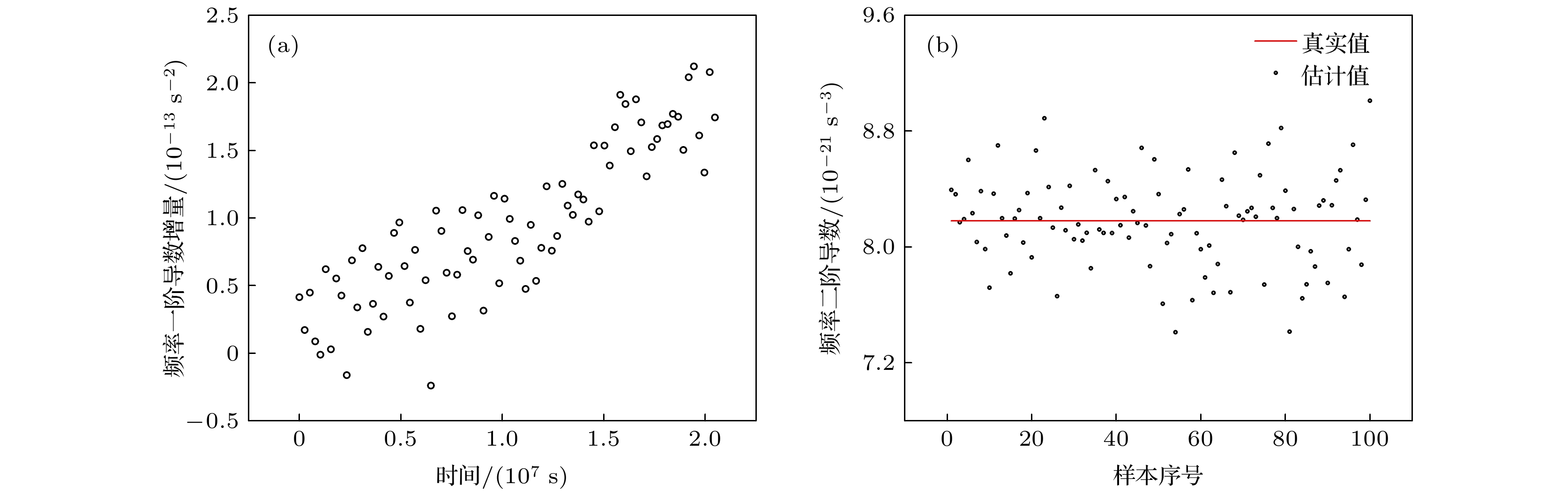
-
航天器处X 射线脉冲星观测信号模拟对脉冲星信号处理方法及导航方案的验证具有重要意义. 通过建立航天器处光子到达时间与相位之间的关系, 可显著提高脉冲星信号模拟算法的效率. 目前建立的航天器处光子到达时间与相位之间关系模型并未考虑接收信号频率变化, 模拟精度较低. 针对这一问题, 本文建立了考虑频率一、二阶导数时的光子到达时间与相位关系模型, 并基于该模型给出航天器处观测信号模拟方法, 提高了脉冲星观测信号模拟算法精度. 仿真实验证明, 相比于迭代法或实时计算航天器处光子到达速率函数的方法, 利用推导的光子到达时间与相位关系模型, 仿真速度最高可提高3个数量级, 保证了信号模拟算法的高效率; 且相比于未考虑频率变化的情况, 由包含频率一、二阶导数的模型得到的Pearson相关系数最高可提高350.0%, 显著提高了计算精度.
-
关键词:
- X 射线脉冲星导航 /
- 脉冲星信号模拟 /
- 频率变化 /
- Pearson相关系数
The simulation of X-ray pulsar observation signals at spacecraft is of great significance in verifying pulsar signal processing methods and navigation schemes. The efficiency of pulsar signal simulation algorithm can be significantly improved by establishing the relationship between photon arrival time and phase at spacecraft. At present, the frequency change of the received pulsar signal is not considered in the model for the relation between photon arrival time and phase at spacecraft, which leads the calculation accuracy to decrease greatly. To solve this problem, a model for the relation between photon arrival time and phase is established with the first derivative and second derivative of frequency taken into consideration. Based on this model, a new simulation method of observation pulsar signal at a spacecraft is proposed, which not only ensures high efficiency, but also improves the simulation accuracy. The proposed method is verified from three aspects. Firstly, the correctness of the proposed method is proved by comparing the cumulative pulse profile from the simulation data with the standard pulse profile, and the results show that the standard pulse profile can be recovered by the simulation data from the proposed method. Secondly, through the comparison of experimental results with the observational data from RXTE (Rossi X-ray timing Explorer), the correctness of the proposed method is further verified. The experimental comparison results show that the absolute difference in searched frequency between simulated data and observational data for the Crab pulsar is less than 10–4, which sufficiently validates the method. Finally, the simulation efficiency and accuracy of the proposed method are compared with those of other methods to prove the superiority of the proposed method over the existing methods. The comparison results show that the simulation speed of the proposed method can be increased by up to 3 orders of magnitude compared with that of the iterative method or the method of establishing the real-time photon arrival rate function at the spacecraft, which ensures the high efficiency of the signal simulation algorithm. And comparing with the case without considering the frequency change, the Pearson correlation coefficient is increased by up to 350.0%, significantly improving the calculation accuracy. The proposed method can be used to verify the X-ray pulsar signal processing and navigation algorithms.-
Keywords:
- X-ray pulsar-based navigation /
- pulsar signal simulation /
- frequency variation /
- Pearson correlation coefficient
[1] Wood K S 1993 Proceedings of SPIE - The International Society for Optical Engineering, Washington, September 16, 1993 p105
[2] Sheikh S I 2005 Ph. D. Dissertation (Maryland: University of Maryland)
[3] 郑世界, 葛明玉, 韩大炜, 王文彬, 陈勇, 卢方军, 鲍天威, 柴军营, 董永伟, 冯旻子, 贺健健, 黄跃, 孔敏南, 李汉成, 李陆, 李正恒, 刘江涛, 刘鑫, 师昊礼, 宋黎明, 孙建超, 王瑞杰, 王源浩, 文星, 吴伯冰, 肖华林, 熊少林, 许寒晖, 徐明, 张娟, 张来宇, 张力, 张晓峰, 张永杰, 赵一, 张双南 2017 中国科学: 物理学 力学 天文学 47 116
Zheng S J, Ge M Y, Han D W, Wang W B, Chen Y, Lu F J, Bao T W, Chai J Y, Dong Y W, Feng M Z, He J J, Huang Y, Kong M N, Li H C, Li L, Li Z H, Liu J T, Liu X, Shi H L, Song L M, Sun J C, Wang R J, Wang Y H, Wen X, Wu B B, Xiao H L, Xiong S L, Xu H H, Xu M, Zhang J, Zhang L Y, Zhang L, Zhang X F, Zhang Y J, Zhao Y, Zhang S N 2017 Sci. Sin-Phy. Mech. As. 47 116
[4] Zhang X Y, Shuai P, Huang L W, Chen S L, Xu L H, Vahala L L 2017 Int. J. Aerospace Eng. 2017 8561830
[5] 张大鹏, 王奕迪, 姜坤, 郑伟 2018 宇航学报 39 412
Google Scholar
Zhang D P, Wang Y D, Jiang K, Zheng W 2018 J. Astron. 39 412
Google Scholar
[6] Hang L W, Shuai P, Zhang X Y, Chen S 2019 J. Astron. Telesc. Inst. 5 018003
[7] Zhang S N, Li T P, Lu F J, Song L M, Zhuang R L 2020 Sci. China Phys. Mech. 63 249502
Google Scholar
[8] Chen Y, Cui W W, Li W, Wang J, Xu Y P, Lu F J, Wang Y S, Chen T X, Han D W, Hu W, Zhang Y, Huo J, Yang Y J, Li M S, Lu B, Zhang Z L, Li T P, Zhang S N, Xiong S L, Zhang S, Xue R F, Zhao X F, Zhu Y, Zhu Y X, Liu H W, Yang Y J, Zhang F 2020 Sci. China Phys. Mech. 63 49
[9] Winternitz L, Mitchell J W, Hassouneh M A, Valdez J E, Price S R, Semper S R, Yu W H, Wood K S, Arzoumanian Z, Ray P, Gendreau K C 2016 2016 IEEE Aerospace Conference Big Sky, USA, March 5–12, 2016 p8
[10] Yu W H, Semper S R, Mitchell J W, Winternitz L B, Arzoumanian Z 2020 Acta Astronaut. 176 531
Google Scholar
[11] 胡慧君, 赵宝升, 盛立志, 鄢秋荣 2011 60 029701
Google Scholar
Hu H J, Zhao B S, Sheng L Z, Yan Q R 2011 Acta Phys. Sin. 60 029701
Google Scholar
[12] 孙海峰, 谢楷, 李小平, 方海燕, 刘秀平, 傅灵忠, 孙海建, 薛梦凡 2013 62 956
Google Scholar
Sun H F, Xie K, Li X P, Fang H Y, Liu X P, Sun H J, Xue M F 2013 Acta Phys. Sin. 62 956
Google Scholar
[13] 周峰, 吴光敏, 赵宝升, 盛立志, 宋娟, 刘永安, 鄢秋荣, 邓宁勤, 赵建军 , rhhz_volume 2013 rhhz_volume 62 119701
Google Scholar
Zhou F, Wu G M, Zhao B S, Sheng L Z, Song J, Liu Y A, Yan Q R, Deng N Q, Zhao J J 2013 Acta Phys. Sin. 62 119701
Google Scholar
[14] 刘利, 郑伟, 汤国建, 孙守明 2012 国防科技大学学报 34 5
Google Scholar
Liu L, Zheng W, Tang G J, Sun S M 2012 J. Natl. Univ. Def. Technol. 34 5
Google Scholar
[15] Li X P, Xue M F, Fang H Y, Liu B, Sun H F, Liu Y 2017 IEEE T. Ind. Electron. 64 1
Google Scholar
[16] Emadzadeh A A, Speyer J L 2010 IEEE T. Signal Proces. 58 4484
Google Scholar
[17] Zhang H, Xu L P, Song S B, Jiao R 2014 Acta Astronaut. 98 189
Google Scholar
[18] Jin J, Liu Y X, Li X Y, Shen Y, Huang L W 2016 2016 IEEE International Conference on Mechatronics and Automation Harbin, China, August 7–10, 2016 p1
[19] Fu L Z, Shuai P, Xue M F, Sun H F, Fang H Y 2015 China Satellite Navigation Conference Xi’an, China, May 13–15, 2015 p635
[20] 邓永录, 梁之舜 1998 随机点过程及其应用 (北京: 科学出版社) 第100—106 页
Deng Y L, Liang Z S 1998 Stochastic Point Process and Its Application (Beijing: Science Press) pp100–106 (in Chinese)
[21] 薛梦凡, 李小平, 孙海峰, 刘兵, 方海燕, 沈利荣 2015 64 219701
Google Scholar
Xue M F, Li X P, Sun H F, Liu B, Fang H Y, Shen L R 2015 Acta Phys. Sin. 64 219701
Google Scholar
[22] Su J Y, Fang H Y, Bao W M, Sun H F, Zhao L 2020 Acta Astronaut. 166 93
Google Scholar
[23] Emadzadeh A A, Speyer J L 2011 IEEE Trans. Aerosp. Electron. Syst. 47 2317
Google Scholar
[24] Emadzadeh A A, Speyer J L 2010 IEEE Transactions on Signal Processing 58 4484
[25] 宁如云 2012 高等数学研究 15 86
Google Scholar
Ning R Y 2012 Stud. College Math. 15 86
Google Scholar
[26] Hobbs G B, Edwards R T, Manchester R N 2006 Mon. Not. R. Astron. Soc. 369 655
Google Scholar
[27] Edwards R T, Hobbs G B, Manchester R N 2010 Mon. Not. R. Astron. Soc. 372 1549
[28] Emadzadeh A A, Speyer J L 2011 IEEE Trans. Contr. Syst. Tech. 19 1021
Google Scholar
[29] Rinauro R, Colonnese S, Scarano G 2013 Signal Process. 93 326
Google Scholar
[30] 邢富冲 2003 中央民族大学学报:自然科学版 12 12
Xing F C 2003 J. Minzu Univ. China Nat. Sci. Ed. 12 12
-
图 1 航天器处X射线脉冲星信号模拟方法流程图
Fig. 1. Flow chart of X-ray pulsar signal simulation method at spacecraft.
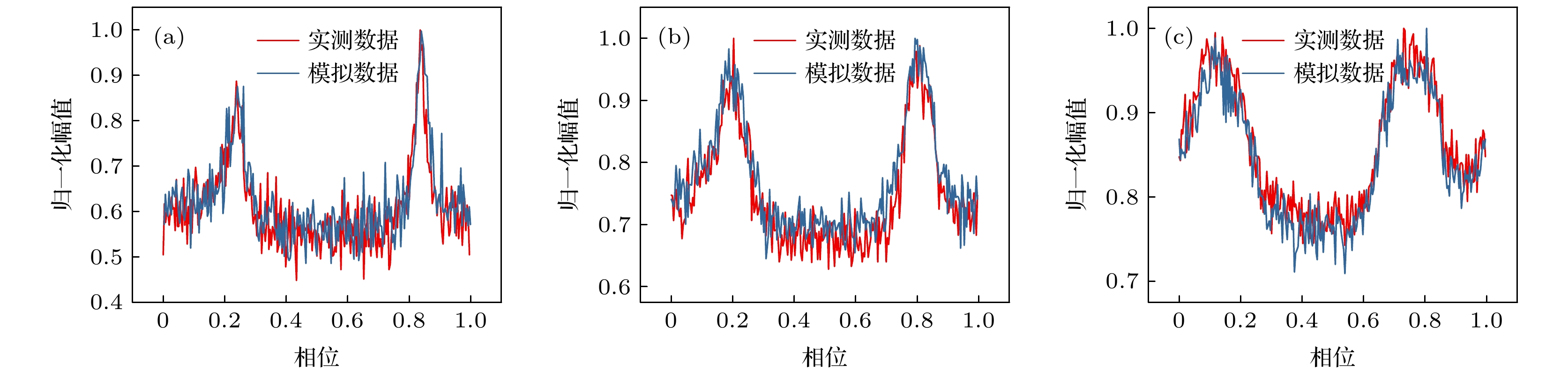
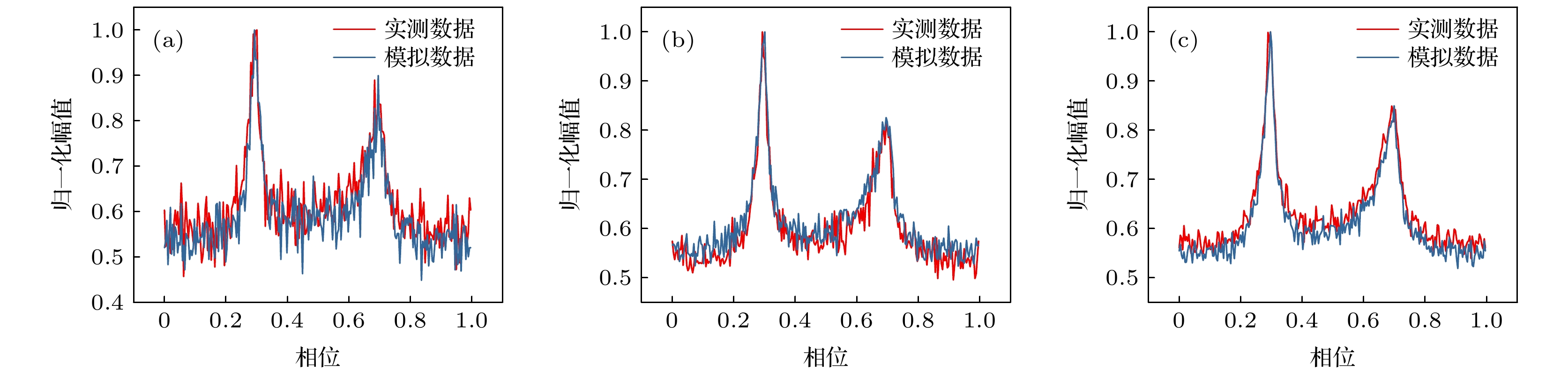
图 2 观测轮廓与标准轮廓的对比 (a) PSR B0531+21 (104s); (b) PSR B1821–24 (104s); (c) PSR B1937+21(104s); (d) PSR B0531+21 (105s); (e) PSR B1821–24 (105s); (f) PSR B1937+21(105s); (g) PSR B0531+21 (106s); (h) PSR B1821–24 (106s); (i) PSR B1937+21(106s)
Fig. 2. Comparison between observed profile and standard profile: (a) PSR B0531+21 (104s); (b) PSR B1821–24 (104s); (c) PSR B1937+21(104s); (d) PSR B0531+21 (105s); (e) PSR B1821–24 (105s); (f) PSR B1937+21(105s); (g) PSR B0531+21 (106s); (h) PSR B1821–24 (106s); (i) PSR B1937+21(106s).
图 3 不同观测时间下未进行时间校正的累积脉冲轮廓 (a) 10 s; (b) 40 s; (c) 90 s
Fig. 3. Cumulative pulse profiles without time correction for different observation times: (a) 10 s; (b) 40 s; (c) 90 s.
图 4 不同观测时间下校正后的累积脉冲轮廓 (a) 10 s; (b) 40 s; (c) 90 s
Fig. 4. Cumulative pulse profiles with time correction for different observation times: (a) 10 s; (b) 40 s; (c) 90 s.
图 5 Pearson相关系数随观测时间的变化曲线 (a) 实测数据实验结果; (b) 模拟数据实验结果
Fig. 5. Variation curves of Pearson correlation coefficient with observation time: (a) Experiment results for observational data; (b) experiment results for simulation data.
图 6 自转频率搜索实验结果 (a) PSR B0531+21; (b) PSR B1821–24; (c) PSR B1937+21
Fig. 6. Rotation frequency search experimental results: (a) PSR B0531+21; (b) PSR B1821–24; (c) PSR B1937+21.
图 7 频率一阶导数检验结果 (a) 模拟数据包得到的待拟合数据; (b) 多次重复实验结果
Fig. 7. First derivative of rotation frequency test results: (a) Data to be fitted from simulated data package; (b) repeated experimental results.
图 8 频率一阶导数检验结果 (a) 模拟数据包得到的待拟合数据; (b) 多次重复实验结果
Fig. 8. First derivative of rotation frequency test results: (a) Data to be fitted from simulated data package; (b) repeated experimental results.
图 9 频率二阶导数检验结果 (a) 模拟数据包得到的待拟合数据; (b) 多次重复实验结果
Fig. 9. Second derivative of rotation frequency test results: (a) Data to be fitted from simulated data package; (b) repeated experimental results.
图 10 方法1与本文方法在不同流量下的仿真速度对比 (a) 仿真时间统计结果; (b) 时间平均值
Fig. 10. Comparison of simulation speed between method 1 and the proposed method under different flux conditions: (a) Simulation time statistics results; (b) time average.
图 11 方法2与本文方法在不同频率下的仿真速度对比 (a) 仿真时间统计结果; (b) 时间平均值
Fig. 11. Comparison of simulation speed between method 2 and the proposed method under different frequencies: (a) Simulation time statistics results; (b) time average.
图 12 两种方法在不同观测时间下的Pearson相关系数对比 (a) PSR B0531+21; (b) PSR B1821–24; (c) PSR B1937+21
Fig. 12. Comparison of Pearson correlation coefficients between two methods for different observation times: (a) PSR B0531+21; (b) PSR B1821–24; (c) PSR B1937+21.
图 A1
$ f(y) $ 的函数图像 (a)$ b = 3{\dot f_{{\text{SC}}}} > 0 $ ; (b)$b = $ $ 3{\dot f_{{\text{SC}}}} > 0$ Fig. A1. Function images of
$ f(y) $ : (a)$ b = 3{\dot f_{{\text{SC}}}} > 0 $ ; (b)$b = $ $ 3{\dot f_{{\text{SC}}}} > 0$ .表 1 初始轨道参数
Table 1. Initial orbit parameters.
轨道参数 参数值 轨道半长轴 6863.0 km 偏心率 0.002 升交点赤经 313.6° 轨道倾角 22.9° 近地点幅角 94.0° 真近点角 26.6° 
下载: 导出CSV
表 2 脉冲星参数
Table 2. Pulsar parameters.
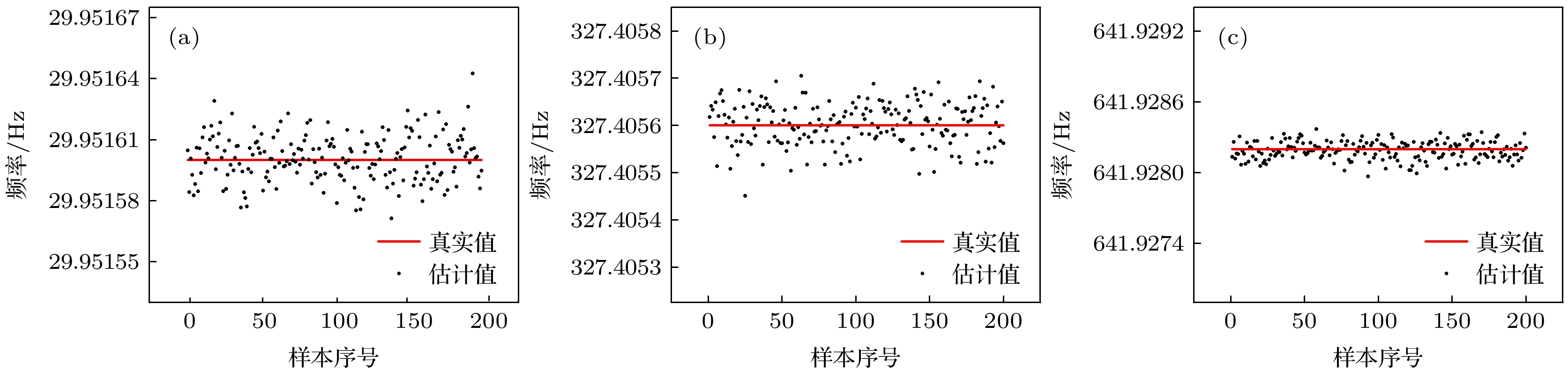
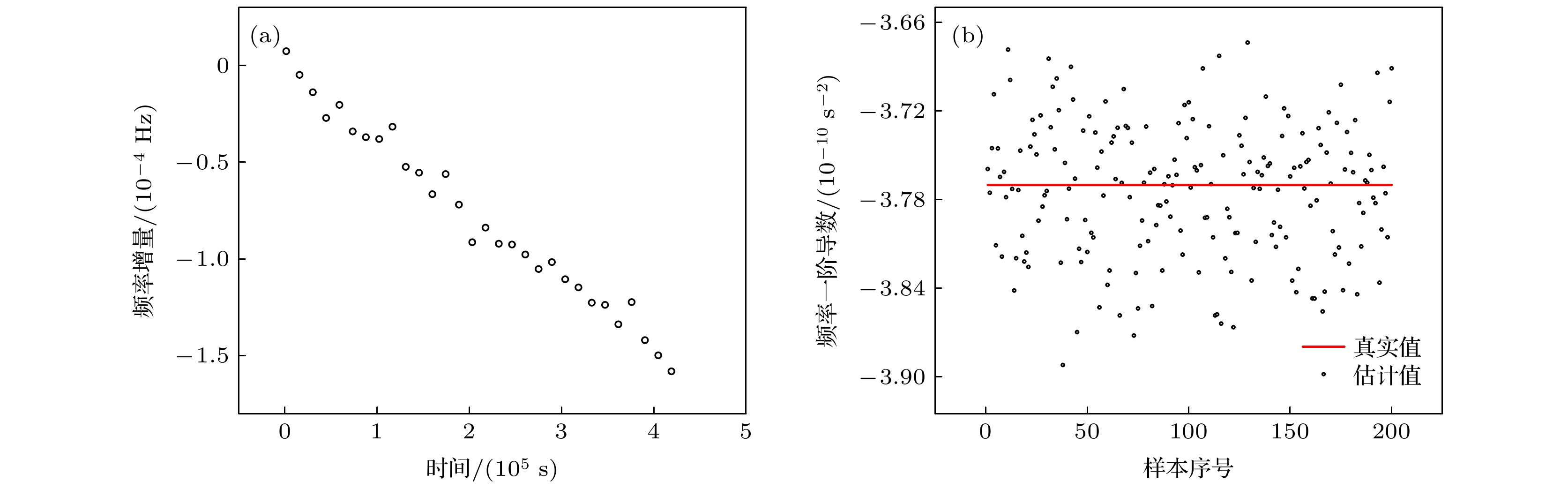
脉冲星 自转频率/s–1 频率一阶项/s–2 频率二阶项/s–3 源流量/背景流量/(photons/s) 赤经/rad 赤纬/rad PSR B0531+21 29.9516 –3.77 × 10–10 8.18 × 10–21 527/10536 1.4597 0.3842 PSR B1821–24 327.4056 –1.73 × 10–13 5.85 × 10–30 0.81/1.87 4.8194 –0.4340 PSR B1937+21 641.9282 –4.33 × 10–14 5.85 × 10–30 0.499/4.5 5.1471 0.3766
下载: 导出CSV
表 3 观测轮廓的Pearson相关系数
Table 3. Pearson coefficients for observation profiles
脉冲星 相关系数 PSR B0531+21 0.999 PSR B1821–24 0.993 PSR B1937+21 0.986
下载: 导出CSV
表 4 数据包95802-01-16-02相关参数
Table 4. Relevant parameters of data packet 95802-01-16-02.
脉冲星 起始观测时间 观测时长/s 平均流量/
(photons·s–1)PSR B0531+21 55465.657384 831.1 5279
下载: 导出CSV
表 5 相位差计算结果
Table 5. Phase difference calculation results.
观测时长/s 相位差1
(未校正)相位差2
(未校正)相位差1 相位差2 10 0.460950 0.457650 0.004947 0.004601 20 0.457154 0.452854 0.003925 0.003905 30 0.477389 0.473673 0.003654 0.003634 40 0.494393 0.490293 0.003435 0.003417 50 0.495135 0.491035 0.003330 0.003260 60 0.487675 0.483475 0.003264 0.003253 70 0.483102 0.479302 0.003222 0.003214 80 0.482691 0.479069 0.003024 0.003016 90 0.485817 0.483317 0.002967 0.002959
下载: 导出CSV
表 6 3种模拟方法效率测试
Table 6. Efficiency test of three simulation methods.
脉冲星 源流量/
背景流量/
(photons·s–1)自转频率/s–1 方法
1/s方法
2/s方法
3/s所提方
法/sPSR B0531+21 527/10536 29.9516 42.05 3.2 0.23 0.41 PSR B1821–24 0.81/1.87 327.4056 0.15 16.2 0.02 0.02 PSR B1937+21 0.499/4.5 641.9282 0.11 36.2 0.01 0.01
下载: 导出CSV
-
[1] Wood K S 1993 Proceedings of SPIE - The International Society for Optical Engineering, Washington, September 16, 1993 p105
[2] Sheikh S I 2005 Ph. D. Dissertation (Maryland: University of Maryland)
[3] 郑世界, 葛明玉, 韩大炜, 王文彬, 陈勇, 卢方军, 鲍天威, 柴军营, 董永伟, 冯旻子, 贺健健, 黄跃, 孔敏南, 李汉成, 李陆, 李正恒, 刘江涛, 刘鑫, 师昊礼, 宋黎明, 孙建超, 王瑞杰, 王源浩, 文星, 吴伯冰, 肖华林, 熊少林, 许寒晖, 徐明, 张娟, 张来宇, 张力, 张晓峰, 张永杰, 赵一, 张双南 2017 中国科学: 物理学 力学 天文学 47 116
Zheng S J, Ge M Y, Han D W, Wang W B, Chen Y, Lu F J, Bao T W, Chai J Y, Dong Y W, Feng M Z, He J J, Huang Y, Kong M N, Li H C, Li L, Li Z H, Liu J T, Liu X, Shi H L, Song L M, Sun J C, Wang R J, Wang Y H, Wen X, Wu B B, Xiao H L, Xiong S L, Xu H H, Xu M, Zhang J, Zhang L Y, Zhang L, Zhang X F, Zhang Y J, Zhao Y, Zhang S N 2017 Sci. Sin-Phy. Mech. As. 47 116
[4] Zhang X Y, Shuai P, Huang L W, Chen S L, Xu L H, Vahala L L 2017 Int. J. Aerospace Eng. 2017 8561830
[5] 张大鹏, 王奕迪, 姜坤, 郑伟 2018 宇航学报 39 412
Google Scholar
Zhang D P, Wang Y D, Jiang K, Zheng W 2018 J. Astron. 39 412
Google Scholar
[6] Hang L W, Shuai P, Zhang X Y, Chen S 2019 J. Astron. Telesc. Inst. 5 018003
[7] Zhang S N, Li T P, Lu F J, Song L M, Zhuang R L 2020 Sci. China Phys. Mech. 63 249502
Google Scholar
[8] Chen Y, Cui W W, Li W, Wang J, Xu Y P, Lu F J, Wang Y S, Chen T X, Han D W, Hu W, Zhang Y, Huo J, Yang Y J, Li M S, Lu B, Zhang Z L, Li T P, Zhang S N, Xiong S L, Zhang S, Xue R F, Zhao X F, Zhu Y, Zhu Y X, Liu H W, Yang Y J, Zhang F 2020 Sci. China Phys. Mech. 63 49
[9] Winternitz L, Mitchell J W, Hassouneh M A, Valdez J E, Price S R, Semper S R, Yu W H, Wood K S, Arzoumanian Z, Ray P, Gendreau K C 2016 2016 IEEE Aerospace Conference Big Sky, USA, March 5–12, 2016 p8
[10] Yu W H, Semper S R, Mitchell J W, Winternitz L B, Arzoumanian Z 2020 Acta Astronaut. 176 531
Google Scholar
[11] 胡慧君, 赵宝升, 盛立志, 鄢秋荣 2011 60 029701
Google Scholar
Hu H J, Zhao B S, Sheng L Z, Yan Q R 2011 Acta Phys. Sin. 60 029701
Google Scholar
[12] 孙海峰, 谢楷, 李小平, 方海燕, 刘秀平, 傅灵忠, 孙海建, 薛梦凡 2013 62 956
Google Scholar
Sun H F, Xie K, Li X P, Fang H Y, Liu X P, Sun H J, Xue M F 2013 Acta Phys. Sin. 62 956
Google Scholar
[13] 周峰, 吴光敏, 赵宝升, 盛立志, 宋娟, 刘永安, 鄢秋荣, 邓宁勤, 赵建军 , rhhz_volume 2013 rhhz_volume 62 119701
Google Scholar
Zhou F, Wu G M, Zhao B S, Sheng L Z, Song J, Liu Y A, Yan Q R, Deng N Q, Zhao J J 2013 Acta Phys. Sin. 62 119701
Google Scholar
[14] 刘利, 郑伟, 汤国建, 孙守明 2012 国防科技大学学报 34 5
Google Scholar
Liu L, Zheng W, Tang G J, Sun S M 2012 J. Natl. Univ. Def. Technol. 34 5
Google Scholar
[15] Li X P, Xue M F, Fang H Y, Liu B, Sun H F, Liu Y 2017 IEEE T. Ind. Electron. 64 1
Google Scholar
[16] Emadzadeh A A, Speyer J L 2010 IEEE T. Signal Proces. 58 4484
Google Scholar
[17] Zhang H, Xu L P, Song S B, Jiao R 2014 Acta Astronaut. 98 189
Google Scholar
[18] Jin J, Liu Y X, Li X Y, Shen Y, Huang L W 2016 2016 IEEE International Conference on Mechatronics and Automation Harbin, China, August 7–10, 2016 p1
[19] Fu L Z, Shuai P, Xue M F, Sun H F, Fang H Y 2015 China Satellite Navigation Conference Xi’an, China, May 13–15, 2015 p635
[20] 邓永录, 梁之舜 1998 随机点过程及其应用 (北京: 科学出版社) 第100—106 页
Deng Y L, Liang Z S 1998 Stochastic Point Process and Its Application (Beijing: Science Press) pp100–106 (in Chinese)
[21] 薛梦凡, 李小平, 孙海峰, 刘兵, 方海燕, 沈利荣 2015 64 219701
Google Scholar
Xue M F, Li X P, Sun H F, Liu B, Fang H Y, Shen L R 2015 Acta Phys. Sin. 64 219701
Google Scholar
[22] Su J Y, Fang H Y, Bao W M, Sun H F, Zhao L 2020 Acta Astronaut. 166 93
Google Scholar
[23] Emadzadeh A A, Speyer J L 2011 IEEE Trans. Aerosp. Electron. Syst. 47 2317
Google Scholar
[24] Emadzadeh A A, Speyer J L 2010 IEEE Transactions on Signal Processing 58 4484
[25] 宁如云 2012 高等数学研究 15 86
Google Scholar
Ning R Y 2012 Stud. College Math. 15 86
Google Scholar
[26] Hobbs G B, Edwards R T, Manchester R N 2006 Mon. Not. R. Astron. Soc. 369 655
Google Scholar
[27] Edwards R T, Hobbs G B, Manchester R N 2010 Mon. Not. R. Astron. Soc. 372 1549
[28] Emadzadeh A A, Speyer J L 2011 IEEE Trans. Contr. Syst. Tech. 19 1021
Google Scholar
[29] Rinauro R, Colonnese S, Scarano G 2013 Signal Process. 93 326
Google Scholar
[30] 邢富冲 2003 中央民族大学学报:自然科学版 12 12
Xing F C 2003 J. Minzu Univ. China Nat. Sci. Ed. 12 12
下载:
计量
- 文章访问数: 4070
- PDF下载量: 84
- 被引次数: 0
