热透镜效应对半整块腔型中二次谐波过程的影响

张晓莉; 王庆伟; 姚文秀; 史少平; 郑立昂; 田龙; 王雅君; 陈力荣; 李卫; 郑耀辉

doi:10.7498/aps.71.20220575

摘要

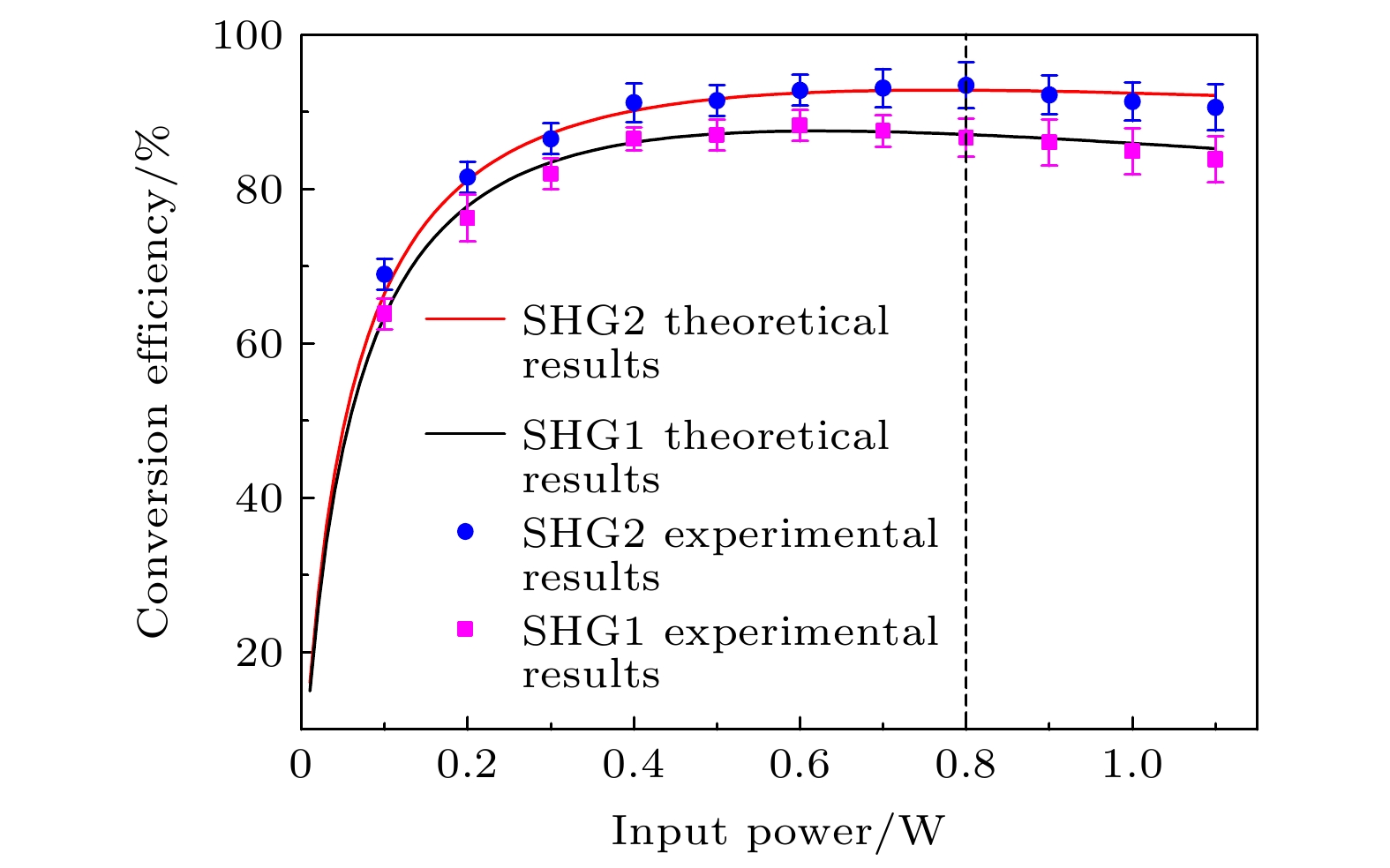
二次谐波过程是制备高功率、宽波长范围激光的有效途径. 在二次谐波过程中, 晶体的热透镜效应是限制转换效率进一步提高的重要因素, 热透镜效应对二次谐波转换效率的影响随着基频光功率的增大而加剧. 本文理论分析了不同半整块腔型中热透镜效应对转换效率的影响关系; 实验上搭建了两种腔型进行高效外腔倍频制备532 nm激光, 测量其倍频转换效率随基频光功率的变化关系. 对于平凹型半整块腔, 在输入光功率为800 mW时, 产生747 mW的532 nm激光输出, 得到最佳的转换效率为93.4% ± 3%; 对于双凹型半整块腔, 在输入光功率为600 mW时, 产生529 mW的532 nm激光输出, 得到的最佳转换效率为88.2% ± 3%. 研究表明, 热透镜效应对双凹型半整块腔的转换效率影响相对较大, 且随着腔内损耗的增加而加剧; 相比于双凹型半整块腔, 平凹型结构可以实现更高效的倍频转换. 本文的理论及实验结果可在量子信息科学、光学频率计量以及生物医学等领域的研究中发挥重要作用.

关键词:

Abstract

Second harmonic generation (SHG) is an effective way to generate short wavelength laser with high power. The SHG is accompanied with the absorptions of fundamental waves and harmonic waves, which converts a fraction of the two waves deposit energy into heat, causing a temperature gradient along the radial direction of the periodically poled potassium titanyl phosphate (PPKTP) crystal. The inhomogeneous temperature distribution causes thermal lensing in the crystal. The thermal lensing effect will deform the spatial mode of the SHG cavity and result in the mode-mismatching of the fundamental wave to the SHG cavity, and therefore the conversion efficiency of SHG process is reduced. Moreover, with the increase of injected fundamental wave power, the influence caused by thermal lens becomes more and more serious. In order to obtain a high-efficiency frequency conversion, it is necessary to take the measure to minimize the effect caused by thermal lensing. In this paper, we report on a high efficiency generation of green laser at 532 nm by external cavity SHG process with a semi-monolithic standing cavity. The influences of thermal lens effect on the optimal conversion efficiency in different semi-monolithic cavities are theoretically analyzed. The variations of conversion efficiency with the pump power in “plane-concave” semi-monolithic cavity based on parallel crystal and also in “concave-concave” semi-monolithic cavity based on concave crystal are quantitatively analyzed. In experiments, two types of cavity structures are built to measure the variation of frequency doubling conversion efficiency with pump power. For the “plane-concave” semi-monolithic cavity, the maximum green laser power of 747 mW is obtained and the corresponding conversion efficiency reaches 93.4%±3%, with 800 mW infrared laser injected. For the “concave-concave” semi-monolithic cavity, the maximum green laser power of 529 mW is obtained and the corresponding conversion efficiency is 88.2% ± 3%, with 600 mW infrared laser injected. The results show that the thermal lens affects the optimal conversion efficiency more seriously in “concave-concave” semi-monolithic cavity than in “plane-concave” semi-monolithic cavity. Furthermore, the influence of thermal lens effect turns higher and higher with the increase of the loss in the cavity. It is obvious that the “plane-concave” semi-monolithic cavity is more suitable for the SHG process and has many potential applications in quantum optics and cold atom physics and provides a guidance for future research on high-efficiency SHG process.

Keywords:

作者及机构信息

1.
山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 田龙, tianlong@sxu.edu.cn

基金项目: 国家重点研发计划(批准号: 2020YFC2200402)、国家自然科学基金(批准号: 62027821, 11874250, 62035015, 12174234)、山西省重点研发计划(批准号: 201903D111001, 202102150101003)和山西省三晋学者特聘教授项目资助的课题.

Authors and contacts

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Tian Long, tianlong@sxu.edu.cn

Funds: Project supported by the National Key R&D Program of China (Grant No. 2020YFC2200402), the National Natural Science Foundation of China (Grants Nos. 62027821, 11874250, 62035015, 12174234), the Key R&D Program of Shanxi, China (Grant Nos. 201903D111001, 202102150101003), and the Program for Sanjin Scholar of Shanxi Province, China.

文章全文 : translate this paragraph

参考文献

[1]	Franken P A, Hill A E, Peters C W, Weinreich G 1961 Phys. Rev. Lett. 7 118 Google Scholar
[2]	Chen X Y, Nadiarynkh O, Plotnikov S, Campagnola P J 2012 Nat. Protoc. 7 654 Google Scholar
[3]	Cicchi R, Pavone F S 2017 Methods Mol. Biol. 1627 409 Google Scholar
[4]	Natal R A, Vassallo J, Paiva G R, Pelegati V B, Barbosa G O, Mendonca G R, Bondarik C, Derchain S F, Carvalho H F, Lima C S, Cesar C L, Sarian L O 2018 Tumor Biol. 40 1 Google Scholar
[5]	Gan X T, Zhao C Y, Hu S Q, Wang T, Song Y, Li J, Zhao Q H, Jie W Q, Zhao J L 2018 Light Sci. Appl. 7 17126 Google Scholar
[6]	Zhao K, Zhang Q, Chini M, Wu Y, Wang X W, Chang Z H 2012 Opt. Lett. 37 3891 Google Scholar
[7]	Rong H, Jones R, Liu A, Cohen O, Hak D, Fang A, Paniccia M 2005 Nature 433 725 Google Scholar
[8]	Gao Y S, Fan Y B, Wang Y J, Yang W H, Song Q H, Xiao S M 2018 Nano Lett. 18 8054 Google Scholar
[9]	张岩, 蔚娟, 杨鹏飞, 张俊香 2022 71 044203 Google Scholar Zhang Y, Yu J, Yang P F, Zhang J X 2022 Acta Phys. Sin. 71 044203 Google Scholar
[10]	Sun X C, Wang Y J, Tian L, Shi S P, Zheng Y H, Peng K C 2019 Opt. Lett. 44 1789 Google Scholar
[11]	张超, 冯晋霞, 李渊骥, 张宽收 2021 量子光学学报 27 8 Google Scholar Zhang C, Feng J X, Li Y J, Zhang K S 2021 J. Quantum Optics 27 8 Google Scholar
[12]	Sun X C, Wang Y J, Tian L, Zheng Y H, Peng K C 2019 Chin. Opt. Lett. 17 072701 Google Scholar
[13]	马亚云, 冯晋霞, 万振菊, 高英豪, 张宽收 2017 66 244205 Google Scholar Ma Y Y, Feng J X, Wan Z J, Gao Y H, Zhang K S 2017 Acta Phys. Sin. 66 244205 Google Scholar
[14]	Ast S, Ast M, Mehmet M, Schnabel R 2016 Opt. Lett. 41 5094 Google Scholar
[15]	万振菊, 冯晋霞, 成健, 张宽收 2018 67 024203 Google Scholar Wan Z J, Feng J X, Cheng J, Zhang K S 2018 Acta Phys. Sin. 67 024203 Google Scholar
[16]	Eberle T, Handchen V, Schnabel R 2013 Opt. Express 21 11546 Google Scholar
[17]	常彦红, 刘阿鹏 2019 量子光学学报 25 297 Google Scholar Chang Y H, Liu A P 2019 J. Quantum Optics 25 297 Google Scholar
[18]	Bao X H, Qian Y, Yang J, Zhang H, Chen Z B, Yang T, Pan J W 2008 Phys. Rev. Lett. 101 190501 Google Scholar
[19]	Yang J, Bao X H, Zhang H, Chen S, Peng C Z, Chen Z B, Pan J W 2009 Phys. Rev. A 80 1042321 Google Scholar
[20]	Mabuchi H, Polzik E S, Kimble H J 1994 J. Opt. Soc. Am. B 11 2023 Google Scholar
[21]	Shiv L, Sorensen J L, Polzik E S, Mizell G 1995 Opt. Lett. 20 2270 Google Scholar
[22]	Maslov V A, Mikhailov V A, Shaunin O P, Shcherbakov I A 1997 Quantum Electron. 27 356 Google Scholar
[23]	Hirohashi J, Pasiskevicius V, Wang S, Laurell F 2007 J. Appl. Phys. 101 033105 Google Scholar
[24]	Ghavami Sabouri S, Chaitanya Kumar S, Khorsandi A, Ebrahim-Zadeh M 2014 IEEE J. Sel. Top. Quant. Electron. 20 7500210 Google Scholar
[25]	Yang W H, Wang Y J, Zheng Y H, Lu H D 2015 Opt. Express 23 19624 Google Scholar
[26]	Innocenzi M E, Yura H T, Fincher C L, Fields R A 1990 Appl. Phys. Lett. 56 1831 Google Scholar
[27]	Hansson G, Karlsson H, Wang S H, Laurell F 2000 Appl. Opt. 39 5058 Google Scholar
[28]	Le Targat R, Zondy J J, Lemonde P 2005 Opt. Commun. 247 471 Google Scholar
[29]	Wen X, Han Y S, Bai J D, He J, Wang Y H, Yang B D, Wang J M 2014 Opt. Express 22 32293 Google Scholar
[30]	Wang Q W, Tian L, Yao W X, Wang Y J, Zheng Y H 2019 Opt. Express 27 28534 Google Scholar
[31]	田龙, 王庆伟, 姚文秀, 李庆回, 王雅君, 郑耀辉 2020 69 044201 Google Scholar Tian L, Wang Q W, Yao W X, Li Q H, Wang Y J, Zheng Y H 2020 Acta Phys. Sin. 69 044201 Google Scholar
[32]	Meier T, Willke B, Danzmann K 2010 Opt. Lett. 35 3742 Google Scholar
[33]	Li G, Li S K, Wang X C, Zhang P F, Zhang T C 2017 Appl. Opt. 56 55 Google Scholar
[34]	Cui X Y, Shen Q, Yan M C, Zeng C, Yuan T, Zhang W Z, Yao X C, Peng C Z, Jiang X, Chen Y A, Pan J W 2018 Opt. Lett. 43 1666 Google Scholar
[35]	Ast S, Nia R M, Schönbeck A, Lastzka N, Steinlechner J, Eberle T, Moritz M, Steinlechner S, Schnabel R 2011 Opt. Lett. 36 3467 Google Scholar
[36]	Yao W X, Wang Q W, Tian L, Li R X, Shi S P, Wang J R, Wang Y J, Zheng Y H 2021 Laser Phys. Lett. 18 015001 Google Scholar
[37]	Wang S, Pasiskevicius V, Laurell F 2004 J. Appl. Phys. 96 2023 Google Scholar
[38]	Roth M, Angert N, Tseitlin M, Alexandrovski A 2001 Opt. Mater. 16 131 Google Scholar
[39]	Kozlovsky W J, Nabors C D, Byer R L 1988 IEEE J. Quantum Electron. 24 913 Google Scholar
[40]	Boyd G D, Kleinman D A 1968 J. Appl. Phys. 39 3597 Google Scholar
[41]	Li Z X, Ma W G, Yang W H, Wang Y J, Zheng Y H 2016 Opt. Lett. 41 3331 Google Scholar
[42]	Chen C Y, Shi S P, Zheng Y H 2017 Rev. Sci. Instrum. 88 103101 Google Scholar
[43]	张宏宇, 王锦荣, 李庆回, 吉宇杰, 贺子洋, 杨荣草, 田龙 2019 量子光学学报 25 456 Google Scholar Zhang H Y, Wang J R, Li Q H, Ji Y J, He Z Y, Yang R C, Tian L 2019 J. Quantum Optics 25 456 Google Scholar
[44]	Wu L A, Kimble H J 1985 J. Opt. Soc. Am. B 2 697 Google Scholar
[45]	Sabaeian M, Jalil-Abadi F S, Rezaee M M, Motazedian A 2014 Opt. Express 22 25615 Google Scholar
[46]	Mousavi L, Sabaeian M, Nadgaran H 2013 Opt. Commun. 300 69 Google Scholar
[47]	Rezaee M M, Sabaeian M, Motazedian A, Jalil-Abadi F S, Askari H, Khazrk I 2015 Appl. Opt. 54 4781 Google Scholar
[48]	Sabaeian M, Jalil-Abadi F S, Rezaee M M, Motazedian A, Shahzadeh M 2015 Appl. Opt. 54 869 Google Scholar
[49]	Wang Y J, Li Z X, Zheng Y H, Su J 2017 IEEE J. Quantum Electron. 53 7000307 Google Scholar

施引文献

图 1 理想情况下模式匹配效率随着基频光输入功率的变化

Fig. 1. Mode-matching efficiency as a function of the input power.

下载: 全尺寸图片幻灯片

图 2 理想情况下转换效率随着输入功率的变化

Fig. 2. Conversion efficiency as a function of input power.

下载: 全尺寸图片幻灯片

图 3 实验装置示意图. OI1—3为光隔离器, EOM为电光调制器, $ \lambda {\text{/2}} $为半波片, PBS1—3为偏振分束器, HR为高反镜, L1—4为模式匹配透镜, LPF1和LPF2为低通滤波器, PID为比例积分微分器, HVA1和HVA2为高压放大器, Mixer1和Mixer2为混频器, DBS1和DBS2为双色分束器, PD1和PD2为光电探测器, SHG1和SHG2为倍频腔, PM1和PM2为功率测量装置

Fig. 3. Schematic of experimental setup. OI1–3, optical isolator; EOM, electro-optic modulator; $ \lambda {\text{/2}} $, half-wave-plate; PBS1–3, polarization beam splitter; HR, high-reflection mirror; L1–4, Lens; LPF1 and LPF2, low-pass filters; PID, proportional-integral-differentiator; HVA1 and HVA2, high-voltage amplifiers; Mixer1 and Mixer2, mixer; DBS1 and DBS2, dichroic beam splitters; PD1 and PD2, photodetectors; SHG1 and SHG2, second harmonic generations; PM1 and PM2, power measurements.

下载: 全尺寸图片幻灯片

图 4 转换效率随输入功率变化的理论和实验结果, 其中误差棒为多次测量误差的平均

Fig. 4. Theoretical and experimental conversion efficiencies as a function of input power. The error bars take the average of multiple measurements.

下载: 全尺寸图片幻灯片

map

[1]	Franken P A, Hill A E, Peters C W, Weinreich G 1961 Phys. Rev. Lett. 7 118 Google Scholar
[2]	Chen X Y, Nadiarynkh O, Plotnikov S, Campagnola P J 2012 Nat. Protoc. 7 654 Google Scholar
[3]	Cicchi R, Pavone F S 2017 Methods Mol. Biol. 1627 409 Google Scholar
[4]	Natal R A, Vassallo J, Paiva G R, Pelegati V B, Barbosa G O, Mendonca G R, Bondarik C, Derchain S F, Carvalho H F, Lima C S, Cesar C L, Sarian L O 2018 Tumor Biol. 40 1 Google Scholar
[5]	Gan X T, Zhao C Y, Hu S Q, Wang T, Song Y, Li J, Zhao Q H, Jie W Q, Zhao J L 2018 Light Sci. Appl. 7 17126 Google Scholar
[6]	Zhao K, Zhang Q, Chini M, Wu Y, Wang X W, Chang Z H 2012 Opt. Lett. 37 3891 Google Scholar
[7]	Rong H, Jones R, Liu A, Cohen O, Hak D, Fang A, Paniccia M 2005 Nature 433 725 Google Scholar
[8]	Gao Y S, Fan Y B, Wang Y J, Yang W H, Song Q H, Xiao S M 2018 Nano Lett. 18 8054 Google Scholar
[9]	张岩, 蔚娟, 杨鹏飞, 张俊香 2022 71 044203 Google Scholar Zhang Y, Yu J, Yang P F, Zhang J X 2022 Acta Phys. Sin. 71 044203 Google Scholar
[10]	Sun X C, Wang Y J, Tian L, Shi S P, Zheng Y H, Peng K C 2019 Opt. Lett. 44 1789 Google Scholar
[11]	张超, 冯晋霞, 李渊骥, 张宽收 2021 量子光学学报 27 8 Google Scholar Zhang C, Feng J X, Li Y J, Zhang K S 2021 J. Quantum Optics 27 8 Google Scholar
[12]	Sun X C, Wang Y J, Tian L, Zheng Y H, Peng K C 2019 Chin. Opt. Lett. 17 072701 Google Scholar
[13]	马亚云, 冯晋霞, 万振菊, 高英豪, 张宽收 2017 66 244205 Google Scholar Ma Y Y, Feng J X, Wan Z J, Gao Y H, Zhang K S 2017 Acta Phys. Sin. 66 244205 Google Scholar
[14]	Ast S, Ast M, Mehmet M, Schnabel R 2016 Opt. Lett. 41 5094 Google Scholar
[15]	万振菊, 冯晋霞, 成健, 张宽收 2018 67 024203 Google Scholar Wan Z J, Feng J X, Cheng J, Zhang K S 2018 Acta Phys. Sin. 67 024203 Google Scholar
[16]	Eberle T, Handchen V, Schnabel R 2013 Opt. Express 21 11546 Google Scholar
[17]	常彦红, 刘阿鹏 2019 量子光学学报 25 297 Google Scholar Chang Y H, Liu A P 2019 J. Quantum Optics 25 297 Google Scholar
[18]	Bao X H, Qian Y, Yang J, Zhang H, Chen Z B, Yang T, Pan J W 2008 Phys. Rev. Lett. 101 190501 Google Scholar
[19]	Yang J, Bao X H, Zhang H, Chen S, Peng C Z, Chen Z B, Pan J W 2009 Phys. Rev. A 80 1042321 Google Scholar
[20]	Mabuchi H, Polzik E S, Kimble H J 1994 J. Opt. Soc. Am. B 11 2023 Google Scholar
[21]	Shiv L, Sorensen J L, Polzik E S, Mizell G 1995 Opt. Lett. 20 2270 Google Scholar
[22]	Maslov V A, Mikhailov V A, Shaunin O P, Shcherbakov I A 1997 Quantum Electron. 27 356 Google Scholar
[23]	Hirohashi J, Pasiskevicius V, Wang S, Laurell F 2007 J. Appl. Phys. 101 033105 Google Scholar
[24]	Ghavami Sabouri S, Chaitanya Kumar S, Khorsandi A, Ebrahim-Zadeh M 2014 IEEE J. Sel. Top. Quant. Electron. 20 7500210 Google Scholar
[25]	Yang W H, Wang Y J, Zheng Y H, Lu H D 2015 Opt. Express 23 19624 Google Scholar
[26]	Innocenzi M E, Yura H T, Fincher C L, Fields R A 1990 Appl. Phys. Lett. 56 1831 Google Scholar
[27]	Hansson G, Karlsson H, Wang S H, Laurell F 2000 Appl. Opt. 39 5058 Google Scholar
[28]	Le Targat R, Zondy J J, Lemonde P 2005 Opt. Commun. 247 471 Google Scholar
[29]	Wen X, Han Y S, Bai J D, He J, Wang Y H, Yang B D, Wang J M 2014 Opt. Express 22 32293 Google Scholar
[30]	Wang Q W, Tian L, Yao W X, Wang Y J, Zheng Y H 2019 Opt. Express 27 28534 Google Scholar
[31]	田龙, 王庆伟, 姚文秀, 李庆回, 王雅君, 郑耀辉 2020 69 044201 Google Scholar Tian L, Wang Q W, Yao W X, Li Q H, Wang Y J, Zheng Y H 2020 Acta Phys. Sin. 69 044201 Google Scholar
[32]	Meier T, Willke B, Danzmann K 2010 Opt. Lett. 35 3742 Google Scholar
[33]	Li G, Li S K, Wang X C, Zhang P F, Zhang T C 2017 Appl. Opt. 56 55 Google Scholar
[34]	Cui X Y, Shen Q, Yan M C, Zeng C, Yuan T, Zhang W Z, Yao X C, Peng C Z, Jiang X, Chen Y A, Pan J W 2018 Opt. Lett. 43 1666 Google Scholar
[35]	Ast S, Nia R M, Schönbeck A, Lastzka N, Steinlechner J, Eberle T, Moritz M, Steinlechner S, Schnabel R 2011 Opt. Lett. 36 3467 Google Scholar
[36]	Yao W X, Wang Q W, Tian L, Li R X, Shi S P, Wang J R, Wang Y J, Zheng Y H 2021 Laser Phys. Lett. 18 015001 Google Scholar
[37]	Wang S, Pasiskevicius V, Laurell F 2004 J. Appl. Phys. 96 2023 Google Scholar
[38]	Roth M, Angert N, Tseitlin M, Alexandrovski A 2001 Opt. Mater. 16 131 Google Scholar
[39]	Kozlovsky W J, Nabors C D, Byer R L 1988 IEEE J. Quantum Electron. 24 913 Google Scholar
[40]	Boyd G D, Kleinman D A 1968 J. Appl. Phys. 39 3597 Google Scholar
[41]	Li Z X, Ma W G, Yang W H, Wang Y J, Zheng Y H 2016 Opt. Lett. 41 3331 Google Scholar
[42]	Chen C Y, Shi S P, Zheng Y H 2017 Rev. Sci. Instrum. 88 103101 Google Scholar
[43]	张宏宇, 王锦荣, 李庆回, 吉宇杰, 贺子洋, 杨荣草, 田龙 2019 量子光学学报 25 456 Google Scholar Zhang H Y, Wang J R, Li Q H, Ji Y J, He Z Y, Yang R C, Tian L 2019 J. Quantum Optics 25 456 Google Scholar
[44]	Wu L A, Kimble H J 1985 J. Opt. Soc. Am. B 2 697 Google Scholar
[45]	Sabaeian M, Jalil-Abadi F S, Rezaee M M, Motazedian A 2014 Opt. Express 22 25615 Google Scholar
[46]	Mousavi L, Sabaeian M, Nadgaran H 2013 Opt. Commun. 300 69 Google Scholar
[47]	Rezaee M M, Sabaeian M, Motazedian A, Jalil-Abadi F S, Askari H, Khazrk I 2015 Appl. Opt. 54 4781 Google Scholar
[48]	Sabaeian M, Jalil-Abadi F S, Rezaee M M, Motazedian A, Shahzadeh M 2015 Appl. Opt. 54 869 Google Scholar
[49]	Wang Y J, Li Z X, Zheng Y H, Su J 2017 IEEE J. Quantum Electron. 53 7000307 Google Scholar

[1]	覃赵福, 陈浩, 胡涛政, 陈卓, 王振林. 基于导波驱动相变材料超构表面的基波及二次谐波聚焦. , 2022, 71(3): 034208. doi: 10.7498/aps.71.20211596
[2]	张萌徕, 覃赵福, 陈卓. 基于开口环阵列结构的表面晶格共振产生及二次谐波增强. , 2021, 70(5): 054206. doi: 10.7498/aps.70.20201424
[3]	覃赵福, 陈浩, 胡涛政, 陈卓, 王振林. 基于导波驱动相变材料超构表面的基波及二次谐波聚焦. , 2021, (): . doi: 10.7498/aps.70.20211596
[4]	徐昕, 金雪莹, 胡晓鸿, 黄新宁. 光学微腔中倍频光场演化和光谱特性. , 2020, 69(2): 024203. doi: 10.7498/aps.69.20191294
[5]	曾周晓松, 王笑, 潘安练. 二维过渡金属硫化物二次谐波: 材料表征、信号调控及增强. , 2020, 69(18): 184210. doi: 10.7498/aps.69.20200452
[6]	田龙, 王庆伟, 姚文秀, 李庆回, 王雅君, 郑耀辉. 高效外腔倍频产生426 nm激光的实验研究. , 2020, 69(4): 044201. doi: 10.7498/aps.69.20191417
[7]	关晓通, 傅文杰, 鲁钝, 杨同斌, 鄢扬, 袁学松. 双共焦波导结构二次谐波太赫兹回旋管谐振腔设计. , 2020, 69(6): 068401. doi: 10.7498/aps.69.20191222
[8]	马明宇, 吴晗, 陈卓. 金属开口环谐振器超构分子中二次谐波偏振态的调控. , 2019, 68(21): 214205. doi: 10.7498/aps.68.20190837
[9]	何鹏, 滕浩, 张宁华, 刘阳阳, 王兆华, 魏志义. 腔模可调的高平均功率飞秒激光再生放大器. , 2016, 65(24): 244201. doi: 10.7498/aps.65.244201
[10]	张孔, 白建东, 何军, 王军民. 激光线宽对单次通过PPMgO:LN晶体倍频效率的影响. , 2016, 65(7): 074207. doi: 10.7498/aps.65.074207
[11]	李培丽, 施伟华, 黄德修, 张新亮. 半导体光放大器中垂直双抽运四波混频效应的理论研究. , 2012, 61(8): 084209. doi: 10.7498/aps.61.084209
[12]	方昕, 沈文忠. 多晶硅中的氧碳行为及其对太阳电池转换效率的影响. , 2011, 60(8): 088801. doi: 10.7498/aps.60.088801
[13]	戴玉蓉, 丁德胜. 小瓣数贝塞尔声束的二次谐波. , 2011, 60(12): 124302. doi: 10.7498/aps.60.124302
[14]	曹卫军, 成春芝, 周效信. 原子在双色组合场中产生高次谐波的转换效率与激光波长的关系. , 2011, 60(5): 054210. doi: 10.7498/aps.60.054210
[15]	周城, 高艳侠, 王培吉, 张仲, 李萍. 负折射率材料中二次谐波转换效率的理论分析. , 2009, 58(2): 914-918. doi: 10.7498/aps.58.914
[16]	来国军, 刘濮鲲. W波段二次谐波回旋行波管放大器的模拟与设计. , 2007, 56(8): 4515-4522. doi: 10.7498/aps.56.4515
[17]	陈亮, 梁昌洪, 党晓杰. 非线性左手材料中的二次谐波. , 2007, 56(11): 6398-6402. doi: 10.7498/aps.56.6398
[18]	薛洪惠, 刘晓宙, 龚秀芬, 章东. 聚焦超声波在层状生物媒质中的二次谐波声场的理论与实验研究. , 2005, 54(11): 5233-5238. doi: 10.7498/aps.54.5233
[19]	马晶, 章若冰, 刘博, 朱晨, 柴路, 张伟力, 张志刚, 王清月. 飞秒BBO光参量放大中闲频光二次谐波的产生. , 2005, 54(8): 3675-3679. doi: 10.7498/aps.54.3675
[20]	郑仰东, 李俊庆, 李淳飞. 双振子模型手性分子介质的二次谐波理论. , 2003, 52(2): 372-376. doi: 10.7498/aps.52.372

计量

文章访问数: 4121
PDF下载量: 82
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

热透镜效应对半整块腔型中二次谐波过程的影响