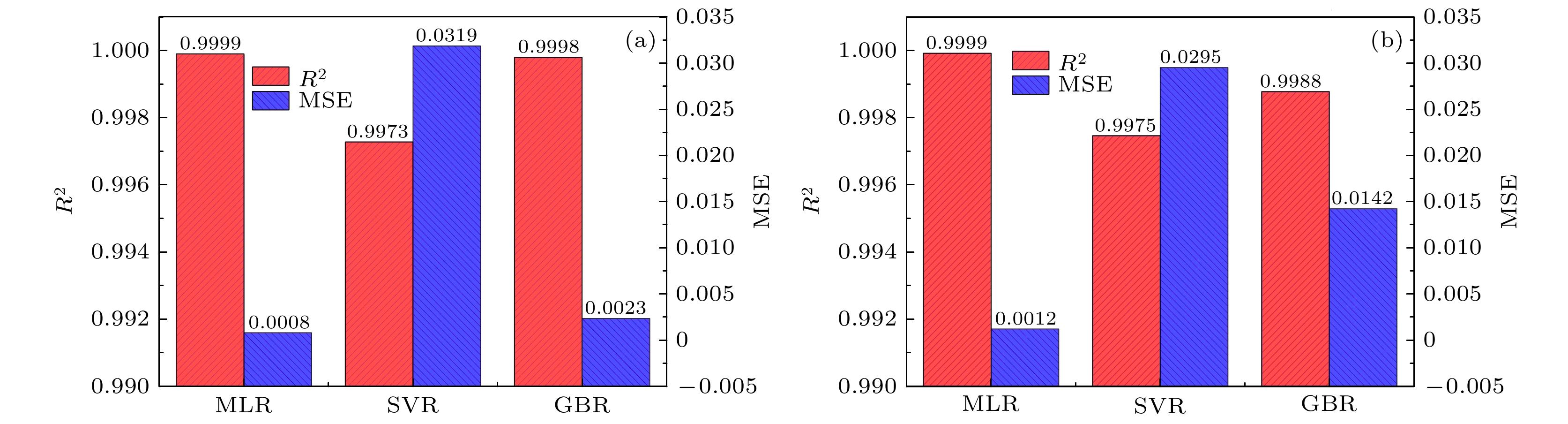
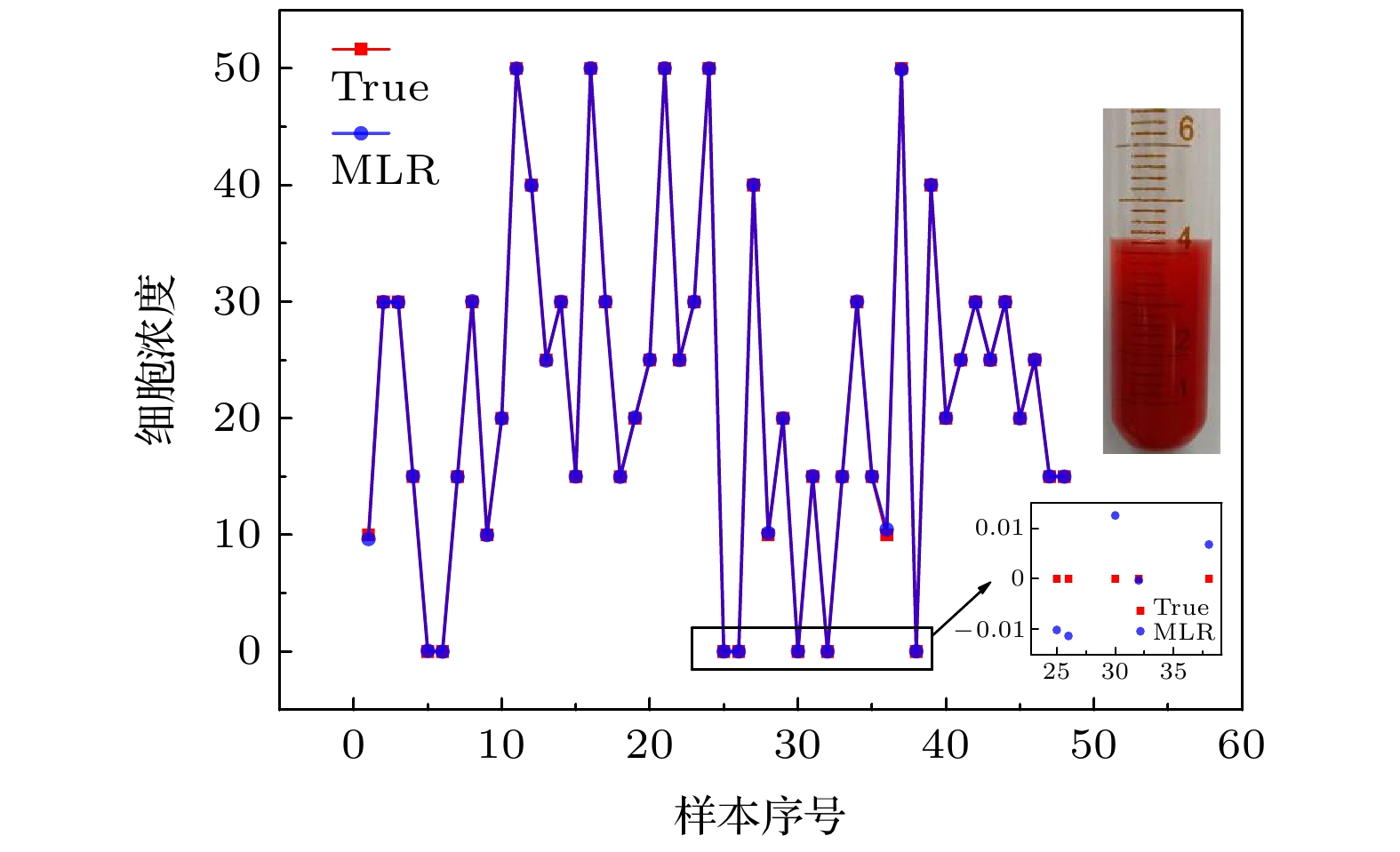
-
基于生物阻抗谱技术提出一种细胞悬浮液浓度自动识别方法, 该方法结合了多元线性回归算法和生物阻抗谱技术, 能够快速准确地识别细胞悬浮液的浓度. 首先, 提出一种细胞位置随机分布策略, 模拟细胞的真实存在状态; 其次, 采用数值仿真的方法生成2400组不同浓度的正常、癌变以及混合的细胞模型并计算生物阻抗谱数据; 然后, 利用多元线性回归、支持向量机和梯度提升三种回归算法分别对癌变细胞浓度进行鉴别, 仿真结果表明, 多元线性回归算法为最佳回归模型, 其平均拟合优度和均方误差分别是0.9997和0.0008; 最后, 将多元线性回归算法应用于不同浓度的红细胞悬浮液的识别中, 实验结果显示其平均拟合优度和均方误差分别是0.9998和0.0079, 说明该方法具有较高的细胞悬浮液浓度识别能力.Based on bioimpedance spectroscopy technology, a method of automatically identifying the cell suspension concentration is proposed. This method combines multiple linear regression algorithm and bioimpedance spectroscopy technology, which can identify the concentration of cell suspension quickly and accurately. Firstly, a strategy of random distribution of cell locations is proposed to simulate the true existence of cells. Secondly, 2400 groups of normal, cancerous and mixed cell models with different concentrations are generated by numerical simulation and their bioimpedance spectroscopy data are calculated.Thirdly, the multiple linear regression algorithm (MLR), support vector machine (SVM), and gradient boosting regression algorithm (GBR) are used to identify the concentration of cancerous cells. The simulation results show that the MLR is the best regression model for cell suspension concentration identification and its average goodness of fit and mean square error are 0.9997 and 0.0008respectively. Finally, the MLR is applied to the identification of red blood cell suspensions with different concentrations, the experimental results show that the average goodness of fit and mean square error are 0.9998 and 0.0079, respectively, indicating that this method has a greater ability to identify cell suspension concentrations.
-
Keywords:
- cell concentration measurement /
- bioimpedance spectroscopy (BIS) /
- multiple linear regression (MLR) /
- random distribution strategy of cell
[1] 付小芬, 熊小波 2017 检验医学与临床 14 274
Google Scholar
Fu X F, Xiong X B 2017 Lab. Med. Clin. 14 274
Google Scholar
[2] 张瑛, 范卫民, 陈哲峰 2005 江苏医药 10 762
Google Scholar
Zhang Y, Fang W M, Chen Z F 2005 Jiangsu. Med. J 10 762
Google Scholar
[3] 任丽蓉, 何蔺, 刘涛, 王浩宇 2020 西部医学 32 1132
Google Scholar
Ren L R, He L, Liu T, Wang H Y 2020 Med. J. West Chin. 32 1132
Google Scholar
[4] 韩莎莎, 郭忠慧, 朱自严 2015 中国输血杂志 28 1463
Google Scholar
Han S S, Guo Z H, Zhu Z Y 2015 Chin. J. Blood Transfusion 28 1463
Google Scholar
[5] 傅怡, 王洋, 白帆, 吴洁, 孙仁, 丁祖蓉, 董澄 2015 医用生物力学 30 392
Google Scholar
Fu Y, Wang Y, Bai F, Wu J, Sun R, Ding Z R, Dong C 2015 J. Med. Biomech. 30 392
Google Scholar
[6] 孔雁, 姜达 2006 中国肿瘤 15 172
Google Scholar
Kong Y, Jiang D 2006 Chin. Cancer 15 172
Google Scholar
[7] Feng Y Q 2009 M. S. Thesis (Changsha: Central South University) (in Chinese)
[8] 杨蕊, 邹明强 2004 分析测试学报 06 124
Google Scholar
Yang R, Zou M Q 2004 J. Instrumental. Anal. 06 124
Google Scholar
[9] Nilsson G E, Zhai H, Chan H P, Farahmand S, Maibach H I 2009 Skin Res. Technol. 15 6
Google Scholar
[10] Guo T, Liu F, Liu Y, Chen N K, Guan B O, Albert J 2014 Biosens. Bioelectron. 55 452
Google Scholar
[11] 杨宇祥, 乔洋 2013 仪器仪表学报 34 908
Google Scholar
Yang Y X, Qiao Y 2013 Chin. J. Sci. Instrum. 34 908
Google Scholar
[12] 姚佳烽, 万建芬, 杨璐, 刘凯, 陈柏, 吴洪涛 2020 69 163301
Google Scholar
Yao J F, Wan J F, Yang L, Liu K, Chen B, Wu H T 2020 Acta Phys. Sin. 69 163301
Google Scholar
[13] 姚佳烽, 姜祝鹏, 徐梓菲, 刘夏移, 陈柏, 吴洪涛 2018 生物化工 4 4
Google Scholar
Yao J F, Jiang Z P, Xu Z F, Liu X Y, Chen B, Wu H T 2018 Biol. Chem. Eng. 4 4
Google Scholar
[14] Sun T P, Ching T S, Cheng C S, Huang S H, Chen Y J, Hsiao C S, Chang C H, Huang S Y, Shieh H L, Liu W H 2010 Cancer Epidemiol. 34 207
Google Scholar
[15] Mellert F, Kai W, Schneider C, Dudykevych T, Preusse C J 2011 IEEE Trans. Biomed. Eng. 58 1511
Google Scholar
[16] Czerniec S A, Ward L C, Lee M J, Refshauge K M, Beith J, Kilbreath S L 2011 Support. Care Cancer 19 703
Google Scholar
[17] 沈继云 2020 信息技术与信息化 5 228
Google Scholar
Shen J Y 2020 Inf. Technol. Informatization 5 228
Google Scholar
[18] 柯鹏飞, 蔡茂国, 吴涛 2020 计算机工程 46 262
Google Scholar
Ke P F, Cai M G, Wu T 2020 Comput. Eng. 46 262
Google Scholar
[19] Kimberly S, Yiqiang S, Lisa G, Heather J, Maureen S, Mendonca E A 2020 Health Inform. J. 26 388
Google Scholar
[20] 刘泉声, 王栋, 朱元广, 杨战标, 伯音 2020 岩土力学 41 319
Google Scholar
Liu Q S, Wang D, Zhu Y G, Yang Z B, Bo Y 2020 Rock Soil Mech. 41 319
Google Scholar
[21] Keprate A, Ratnayake R M C 2017 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM) Singapore, December 10-13, 2017 p1331
[22] 王征征, 张卫钢, 孙道斌, 张鑫, 王培丞 2020 计算机与数字工程 48 546
Google Scholar
Wang Z Z, Zhang W G, Sun D B, Zhang Xin 2020 Comput. Digital Eng. 48 546
Google Scholar
[23] Joshi R P, Qin H, Schoenbach K H 2004 3 rd International Symposium on Nonthermal Medical/Biological Treatments Using Electromagnetic Fields and Ionized Gases San Antonio, TX, the United States of Ameica, June 11–13, 2003 p1677
[24] Jiang Z, Yao J, Wang L, Wu H, Huang J, Zhao T, Takei M 2019 IEEE Sens. J. 19 5979
Google Scholar
[25] Li C, Xu P 2021 Neural Comput. Appl. 33 613
Google Scholar
[26] Smola A J, Schölkopf B 2004 Stat. Comput. 14 199
Google Scholar
[27] Zhang J G, Li Y Y, Cao J 2011 Proceedings of 2011 IEEE International Conference on Computer Science and Automation Engineering Shanghai China, June 10–12, 2011 p47
-
图 2 细胞位置随机分布策略示意图. 蓝色表示正常细胞, 绿色表示癌变细胞
Fig. 2. Schematic diagram of random distribution strategy of cell location. Blue indicates normal cells, and green indicates cancerous cells.
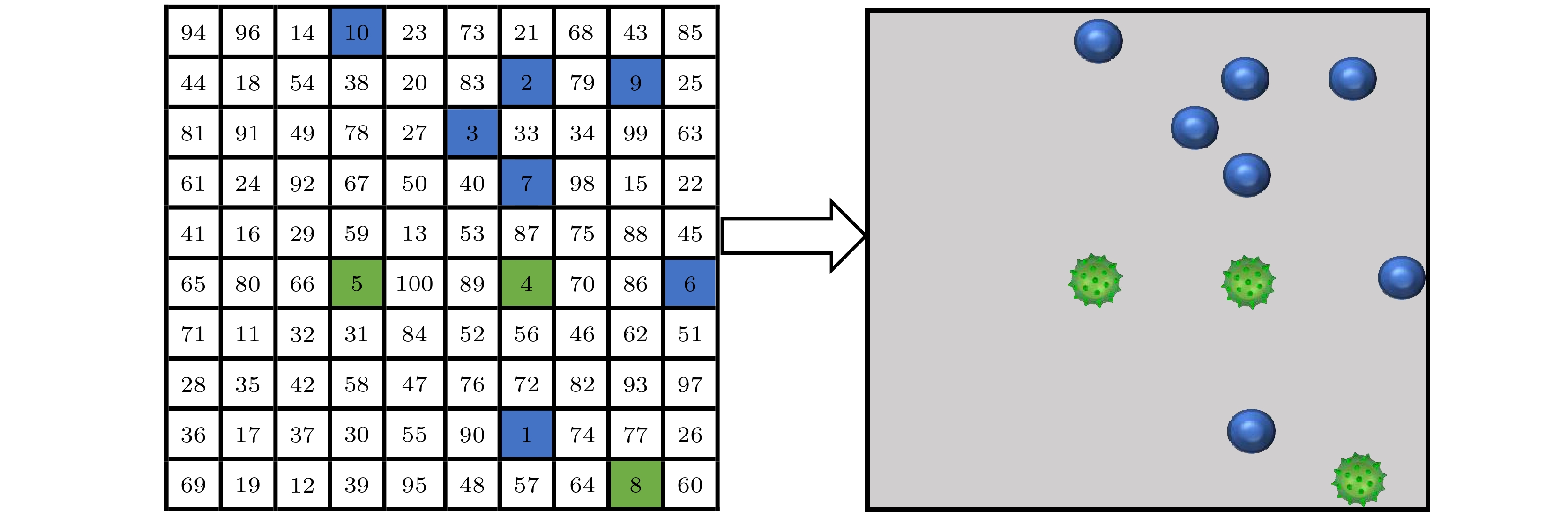
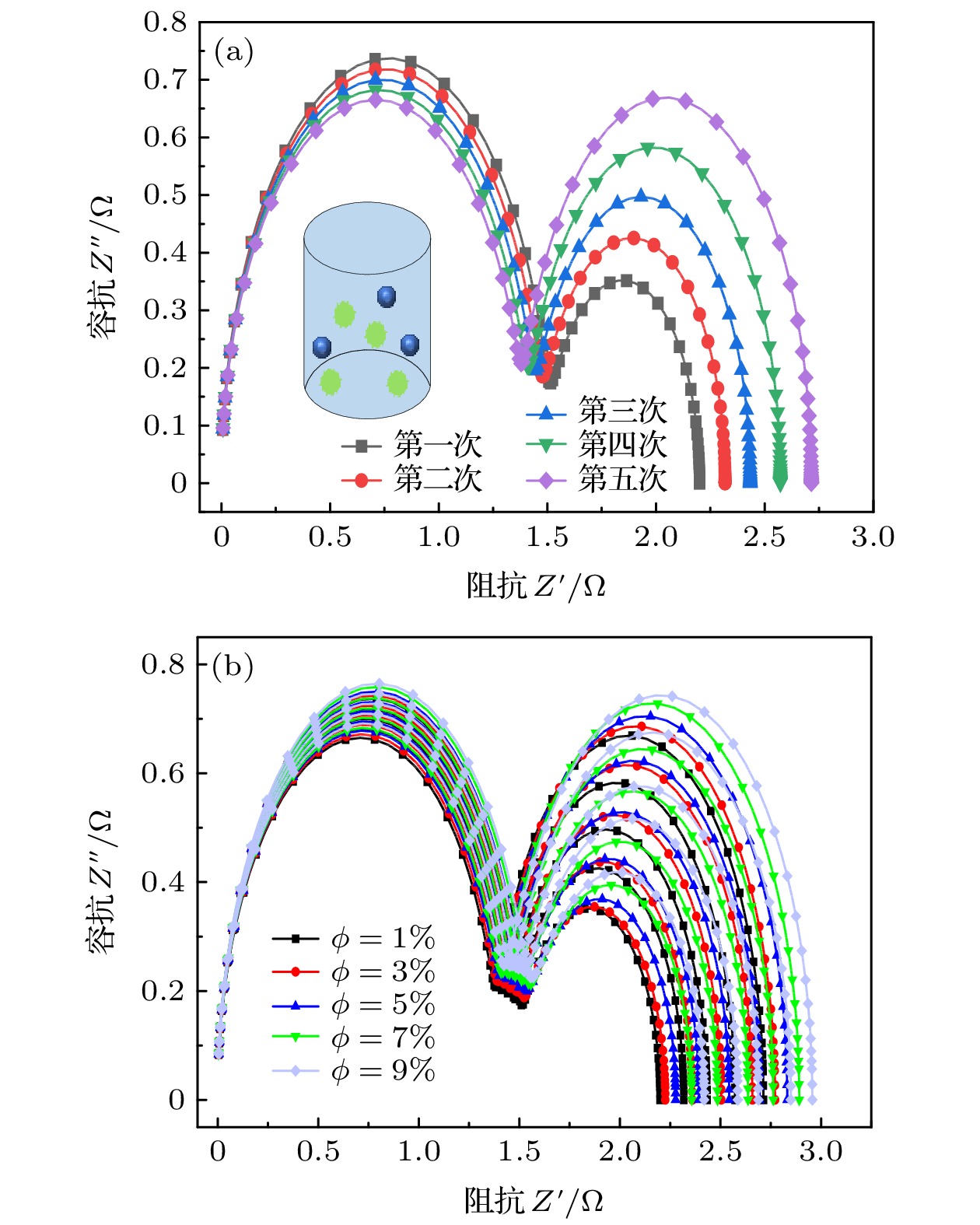
图 3 部分浓度癌变细胞的Nyquist图 (a) 癌变细胞浓度为 1% 时的 5 次细胞随机分布的Nyquist图; (b) 不同癌变细胞浓度的Nyquist图
Fig. 3. Nyquist plot of cancerous cells at partial concentrations: (a) Nyquist plots of randomly distributed cells at 5 times when the concentration of cancerous cells is 1%; (b) Nyquist plots of different cancerous cell concentrations.
图 4 三种回归模型对仿真数据集的训练结果 (a) 训练集的训练结果; (b) 测试集的预测结果
Fig. 4. The training results of the three regression models on the simulation data set: (a) Training results of the training set; (b) predicted results on the test set.
图 5 三种回归模型对部分数据预测值与真实值的差异 (a) 训练集预测值与真实值的差异; (b) 测试集预测值与真实值的差异
Fig. 5. The difference between the predicted value and the true value of partial data by three regression models: (a) The difference between the predicted value of the training set and the true value; (b) the difference between the predicted value of the test set and the true value.
图 6 生物阻抗谱检测实验设备 (a) 实验设备原理图; (b) 传感器结构图
Fig. 6. Bioelectrical impedance spectroscopy instrument: (a) Schematic diagram of experimental equipment; (b) sensor structure diagram.
图 7 MLR对数据集预测值与真实值的差异, 内插图是MLR预测值与真实值的误差放大图像
Fig. 7. The difference between the predicted value and the true value of the data set by MLR. The inset is an enlarged image of the error between the MLR predicted value and the true value.
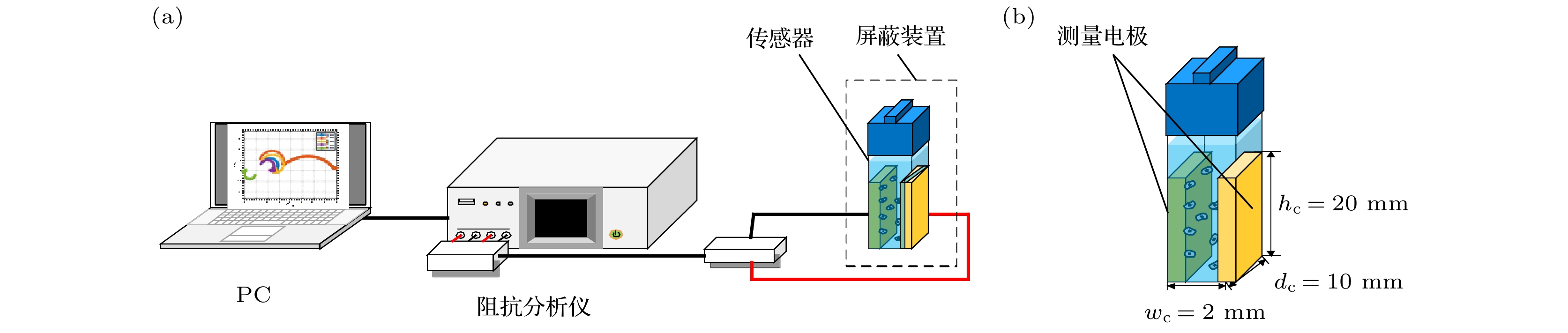
表 1 仿真参数汇总[23]
Table 1. Summary of simulation parameters.
参数 正常B细胞 癌变B细胞 电导率 σ/ (S·m–1) 背景溶液 0.6 0.6 细胞膜 5.6 × 10–5 9.1 × 10–6 细胞质 1.31 0.48 核膜 1.11 × 10–2 4.4 × 10–3 核质 2.04 1.07 相对介电常数 ε 背景溶液 80 80 细胞膜 12.8 9.8 细胞质 60 60 核膜 106 60.3 核质 120 120 几何参数/μm 仿真区域 L × L 20 × 20 20 × 20 电极长度 l 4 4 细胞半径 R1 3.3 5.2 细胞核半径 R2 2.8 4.4 细胞膜厚 d1 0.007 0.007 核膜厚度 d2 0.04 0.04 
下载: 导出CSV
表 2 仿真数据的三种回归算法五折验证结果
Table 2. Validation results of three regression algorithms for simulation data.
MLR SVR GBR R2 MSE R2 MSE R2 MSE 1 0.9999 0.0006 0.0006 0.0257 0.9994 0.0066 2 0.9995 0.0009 0.0009 0.0313 0.9985 0.0171 3 0.9998 0.0006 0.0006 0.0336 0.9986 0.0179 4 0.9999 0.0012 0.0012 0.0267 0.9986 0.0156 5 0.9996 0.0008 0.0008 0.0335 0.9987 0.0176 平均数 0.9997 0.0008 0.0008 0.0302 0.9988 0.0150
下载: 导出CSV
表 3 每种红细胞悬浮液浓度下的平均绝对误差
Table 3. The average absolute error of each red blood cell suspension concentration.
浓度/% 0 10 15 20 25 30 40 50 平均绝对误差 0.0104 0.0124 0.0113 0.0134 0.0129 0.0165 0.0158 0.0161
下载: 导出CSV
表 4 MLR回归算法的五折交叉验证结果
Table 4. Cross validation results of MLR regression algorithm.
1 2 3 4 5 平均数 R2 1.0000 0.9998 0.9999 0.9996 0.9999 0.9998 MSE 0.0015 0.0021 0.0152 0.0035 0.0173 0.0079
下载: 导出CSV
-
[1] 付小芬, 熊小波 2017 检验医学与临床 14 274
Google Scholar
Fu X F, Xiong X B 2017 Lab. Med. Clin. 14 274
Google Scholar
[2] 张瑛, 范卫民, 陈哲峰 2005 江苏医药 10 762
Google Scholar
Zhang Y, Fang W M, Chen Z F 2005 Jiangsu. Med. J 10 762
Google Scholar
[3] 任丽蓉, 何蔺, 刘涛, 王浩宇 2020 西部医学 32 1132
Google Scholar
Ren L R, He L, Liu T, Wang H Y 2020 Med. J. West Chin. 32 1132
Google Scholar
[4] 韩莎莎, 郭忠慧, 朱自严 2015 中国输血杂志 28 1463
Google Scholar
Han S S, Guo Z H, Zhu Z Y 2015 Chin. J. Blood Transfusion 28 1463
Google Scholar
[5] 傅怡, 王洋, 白帆, 吴洁, 孙仁, 丁祖蓉, 董澄 2015 医用生物力学 30 392
Google Scholar
Fu Y, Wang Y, Bai F, Wu J, Sun R, Ding Z R, Dong C 2015 J. Med. Biomech. 30 392
Google Scholar
[6] 孔雁, 姜达 2006 中国肿瘤 15 172
Google Scholar
Kong Y, Jiang D 2006 Chin. Cancer 15 172
Google Scholar
[7] Feng Y Q 2009 M. S. Thesis (Changsha: Central South University) (in Chinese)
[8] 杨蕊, 邹明强 2004 分析测试学报 06 124
Google Scholar
Yang R, Zou M Q 2004 J. Instrumental. Anal. 06 124
Google Scholar
[9] Nilsson G E, Zhai H, Chan H P, Farahmand S, Maibach H I 2009 Skin Res. Technol. 15 6
Google Scholar
[10] Guo T, Liu F, Liu Y, Chen N K, Guan B O, Albert J 2014 Biosens. Bioelectron. 55 452
Google Scholar
[11] 杨宇祥, 乔洋 2013 仪器仪表学报 34 908
Google Scholar
Yang Y X, Qiao Y 2013 Chin. J. Sci. Instrum. 34 908
Google Scholar
[12] 姚佳烽, 万建芬, 杨璐, 刘凯, 陈柏, 吴洪涛 2020 69 163301
Google Scholar
Yao J F, Wan J F, Yang L, Liu K, Chen B, Wu H T 2020 Acta Phys. Sin. 69 163301
Google Scholar
[13] 姚佳烽, 姜祝鹏, 徐梓菲, 刘夏移, 陈柏, 吴洪涛 2018 生物化工 4 4
Google Scholar
Yao J F, Jiang Z P, Xu Z F, Liu X Y, Chen B, Wu H T 2018 Biol. Chem. Eng. 4 4
Google Scholar
[14] Sun T P, Ching T S, Cheng C S, Huang S H, Chen Y J, Hsiao C S, Chang C H, Huang S Y, Shieh H L, Liu W H 2010 Cancer Epidemiol. 34 207
Google Scholar
[15] Mellert F, Kai W, Schneider C, Dudykevych T, Preusse C J 2011 IEEE Trans. Biomed. Eng. 58 1511
Google Scholar
[16] Czerniec S A, Ward L C, Lee M J, Refshauge K M, Beith J, Kilbreath S L 2011 Support. Care Cancer 19 703
Google Scholar
[17] 沈继云 2020 信息技术与信息化 5 228
Google Scholar
Shen J Y 2020 Inf. Technol. Informatization 5 228
Google Scholar
[18] 柯鹏飞, 蔡茂国, 吴涛 2020 计算机工程 46 262
Google Scholar
Ke P F, Cai M G, Wu T 2020 Comput. Eng. 46 262
Google Scholar
[19] Kimberly S, Yiqiang S, Lisa G, Heather J, Maureen S, Mendonca E A 2020 Health Inform. J. 26 388
Google Scholar
[20] 刘泉声, 王栋, 朱元广, 杨战标, 伯音 2020 岩土力学 41 319
Google Scholar
Liu Q S, Wang D, Zhu Y G, Yang Z B, Bo Y 2020 Rock Soil Mech. 41 319
Google Scholar
[21] Keprate A, Ratnayake R M C 2017 2017 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM) Singapore, December 10-13, 2017 p1331
[22] 王征征, 张卫钢, 孙道斌, 张鑫, 王培丞 2020 计算机与数字工程 48 546
Google Scholar
Wang Z Z, Zhang W G, Sun D B, Zhang Xin 2020 Comput. Digital Eng. 48 546
Google Scholar
[23] Joshi R P, Qin H, Schoenbach K H 2004 3 rd International Symposium on Nonthermal Medical/Biological Treatments Using Electromagnetic Fields and Ionized Gases San Antonio, TX, the United States of Ameica, June 11–13, 2003 p1677
[24] Jiang Z, Yao J, Wang L, Wu H, Huang J, Zhao T, Takei M 2019 IEEE Sens. J. 19 5979
Google Scholar
[25] Li C, Xu P 2021 Neural Comput. Appl. 33 613
Google Scholar
[26] Smola A J, Schölkopf B 2004 Stat. Comput. 14 199
Google Scholar
[27] Zhang J G, Li Y Y, Cao J 2011 Proceedings of 2011 IEEE International Conference on Computer Science and Automation Engineering Shanghai China, June 10–12, 2011 p47
下载:
计量
- 文章访问数: 4692
- PDF下载量: 72
- 被引次数: 0
