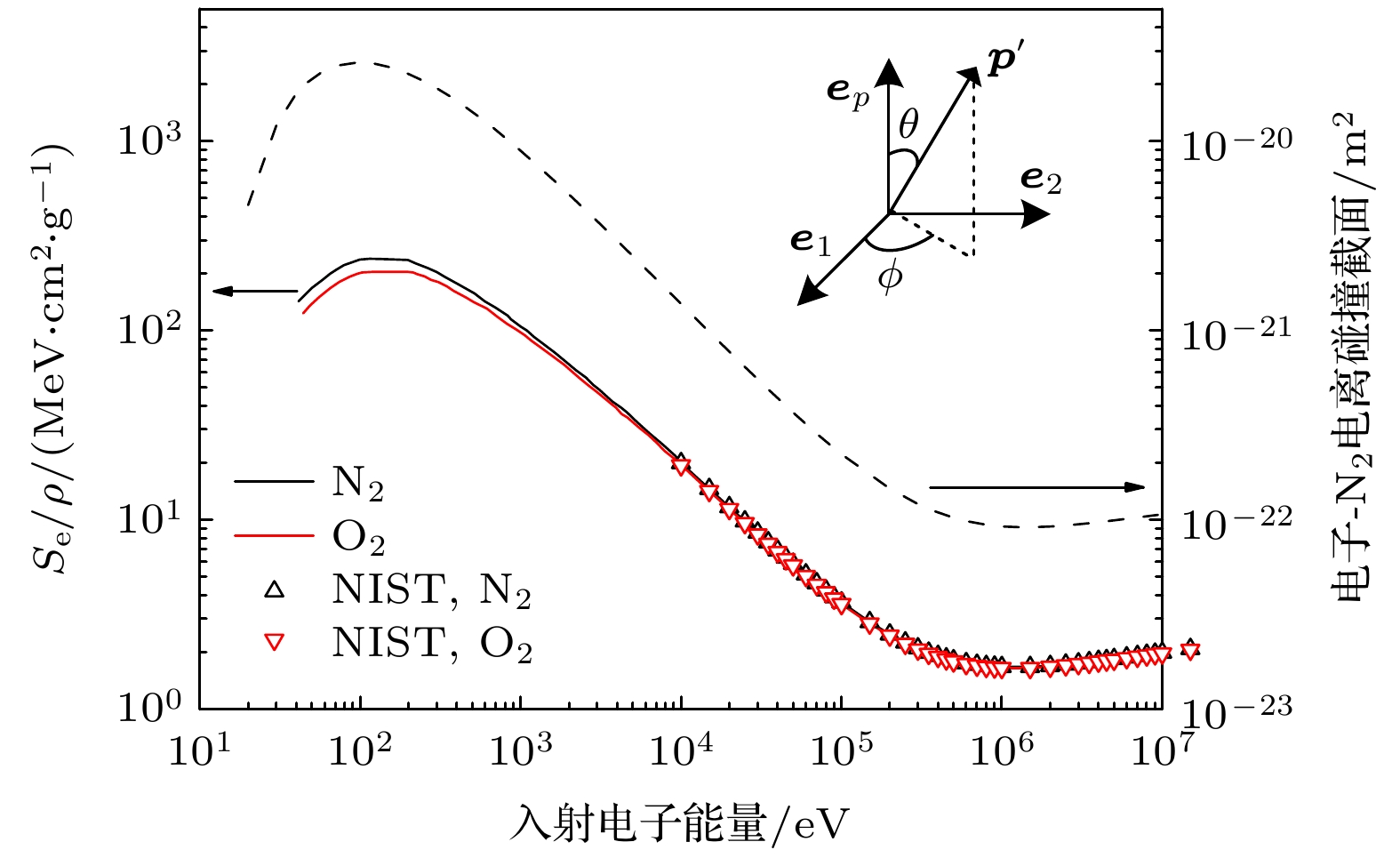
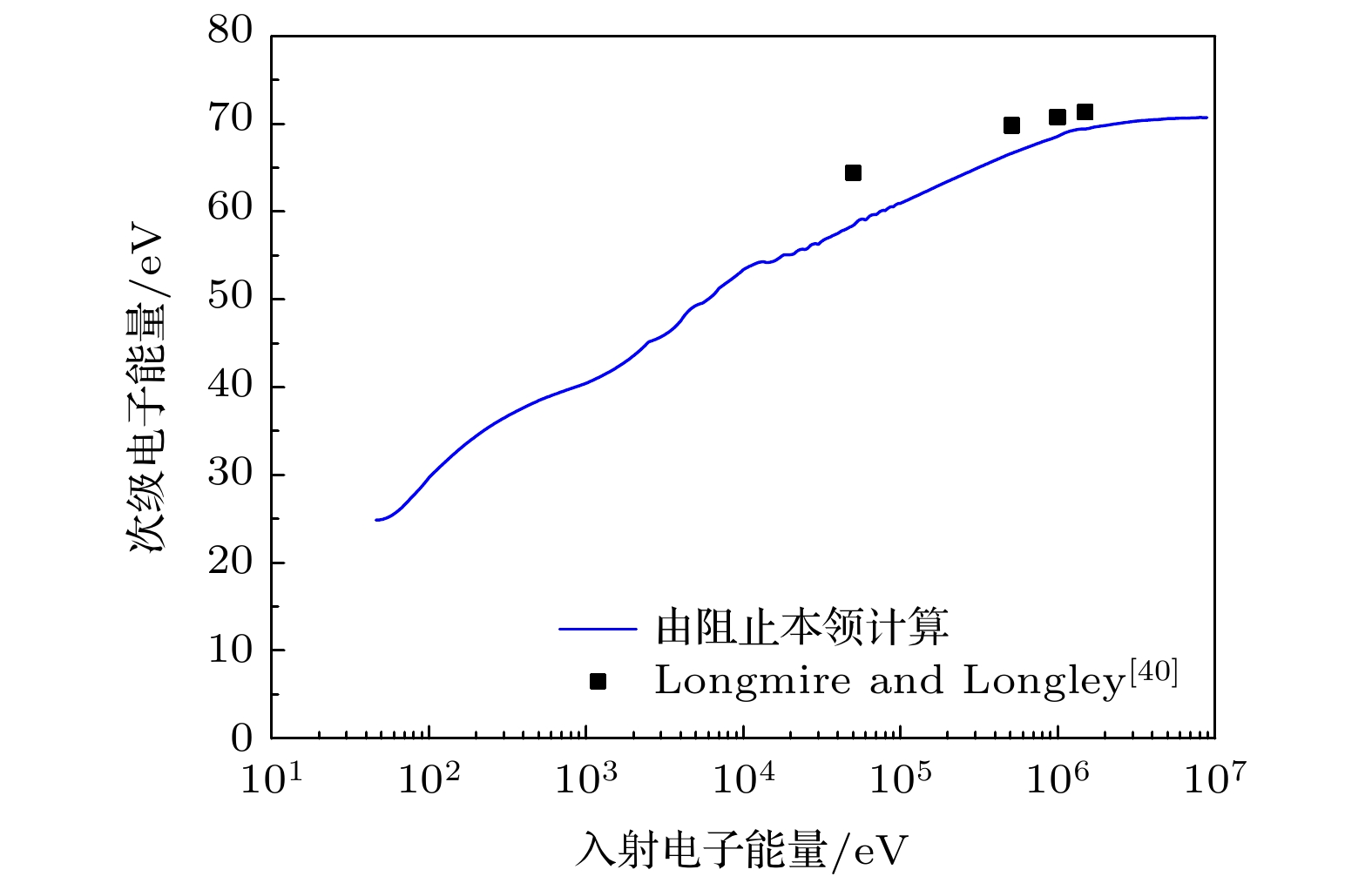
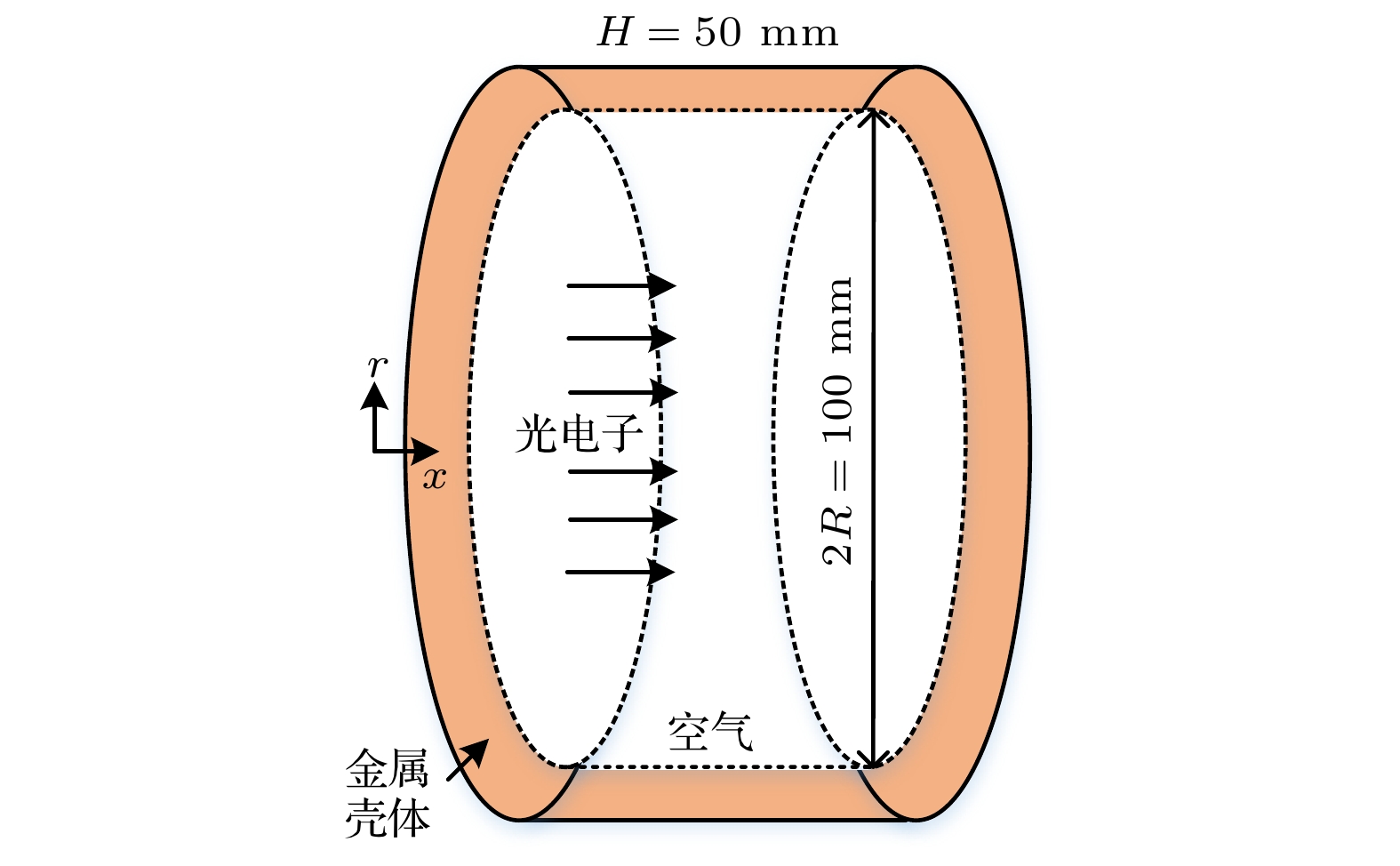
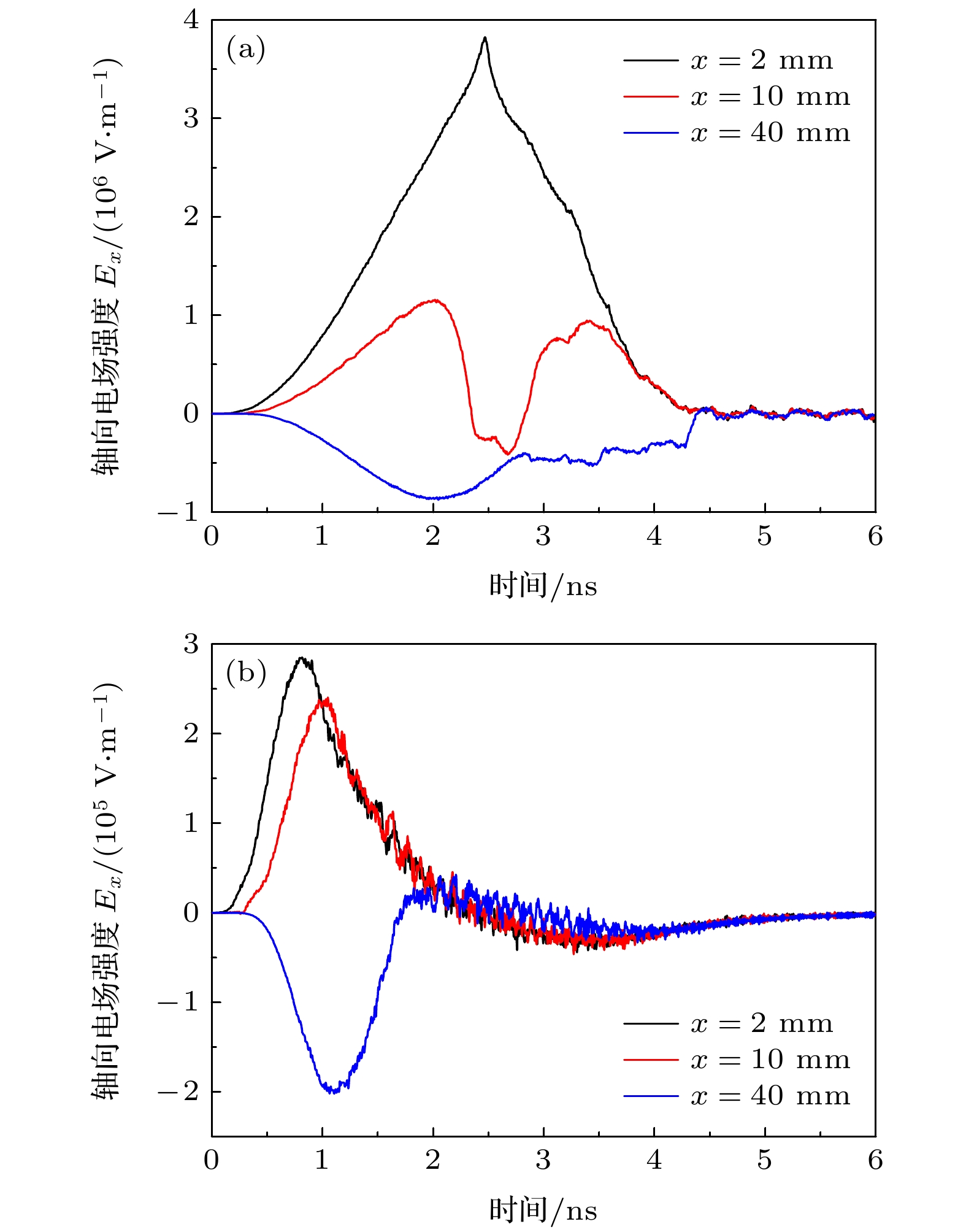
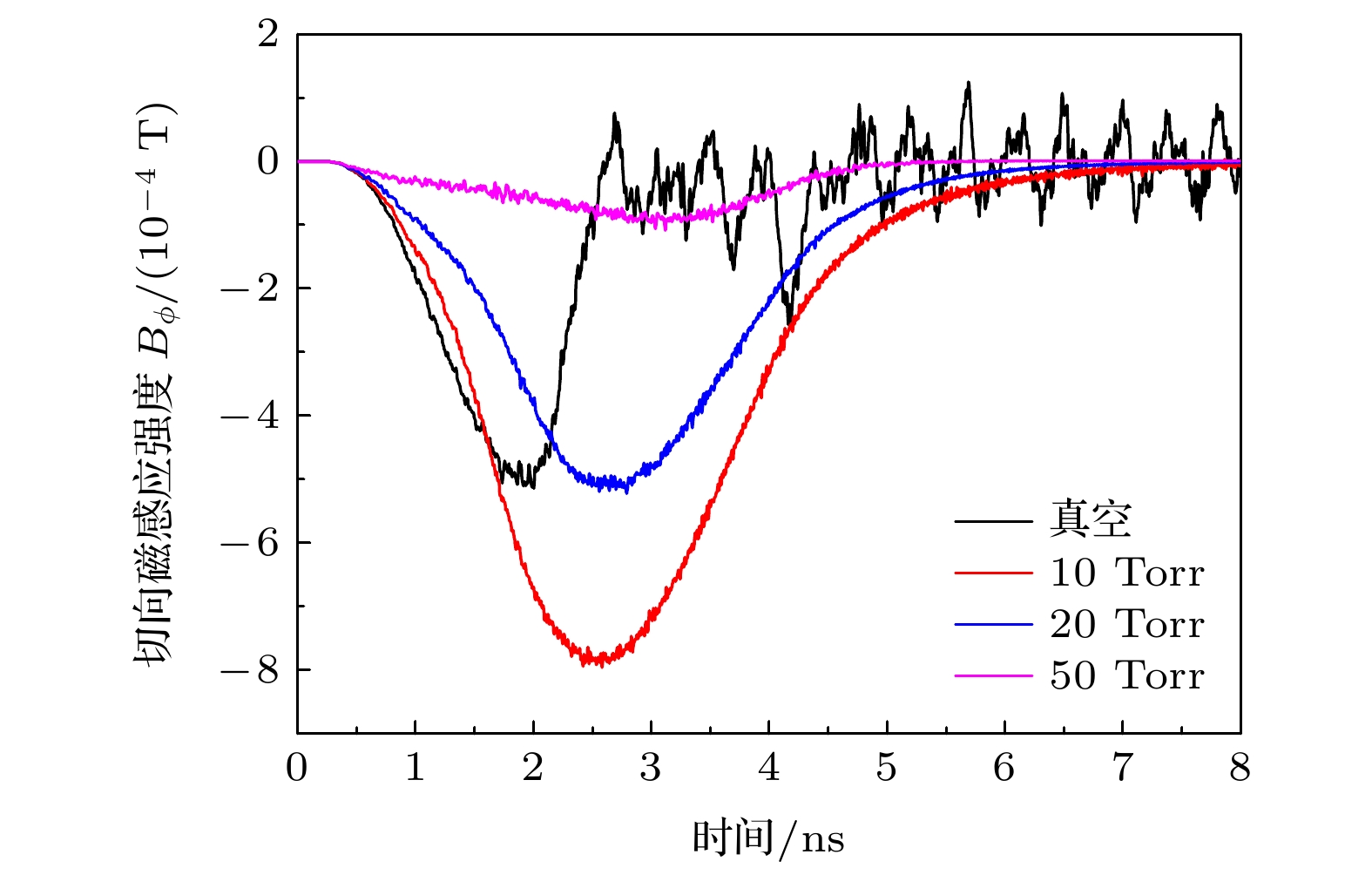
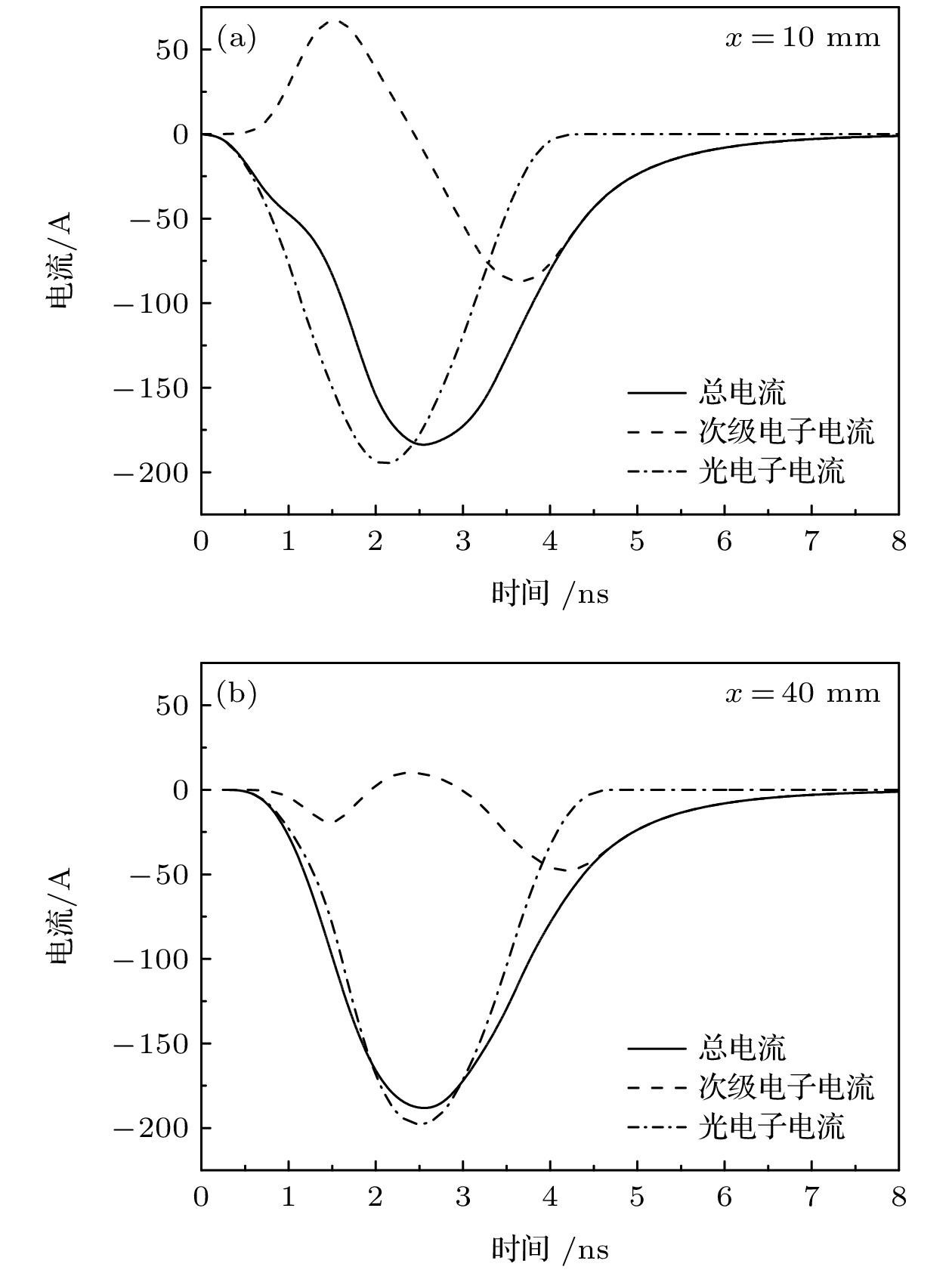
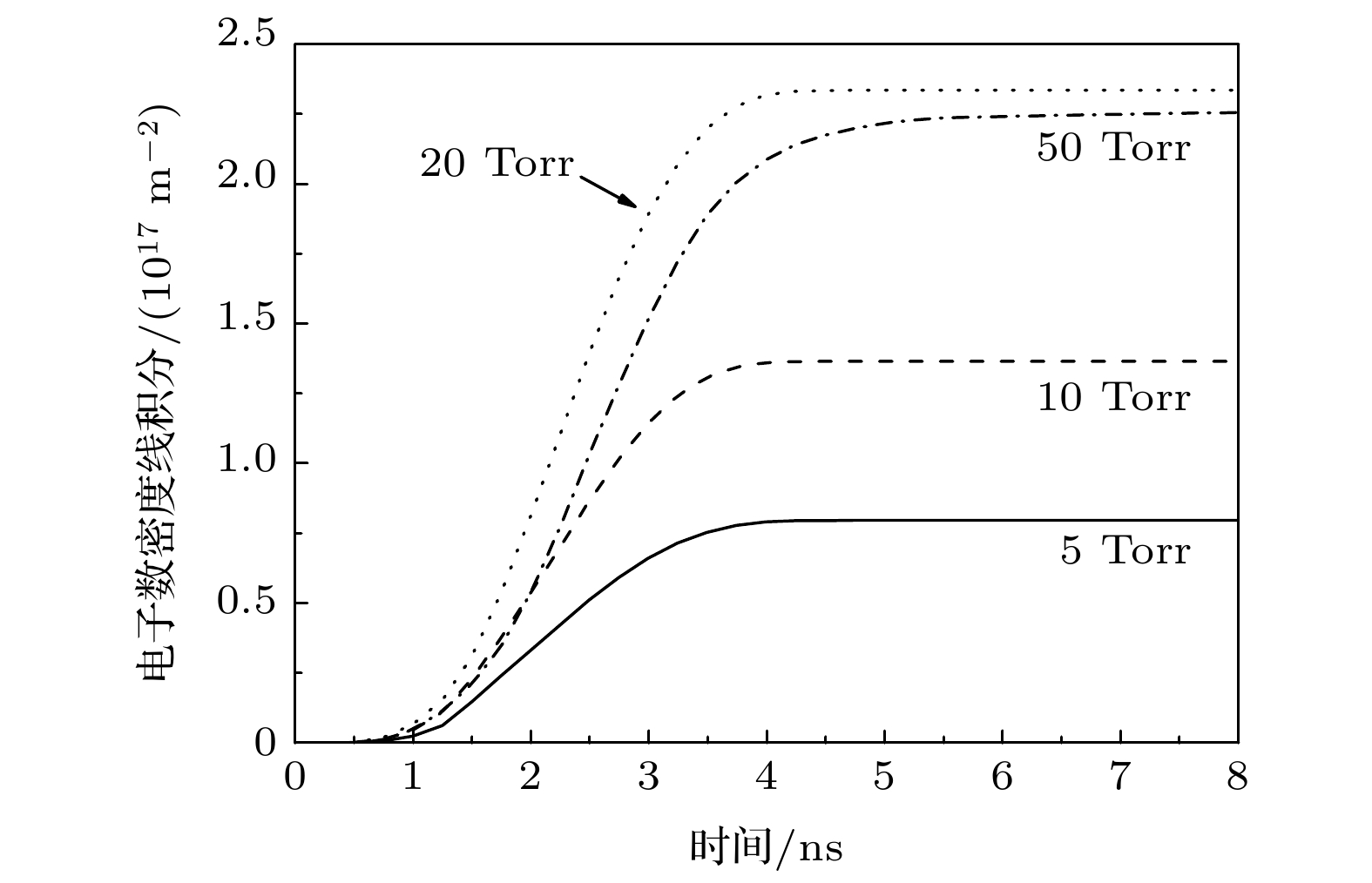
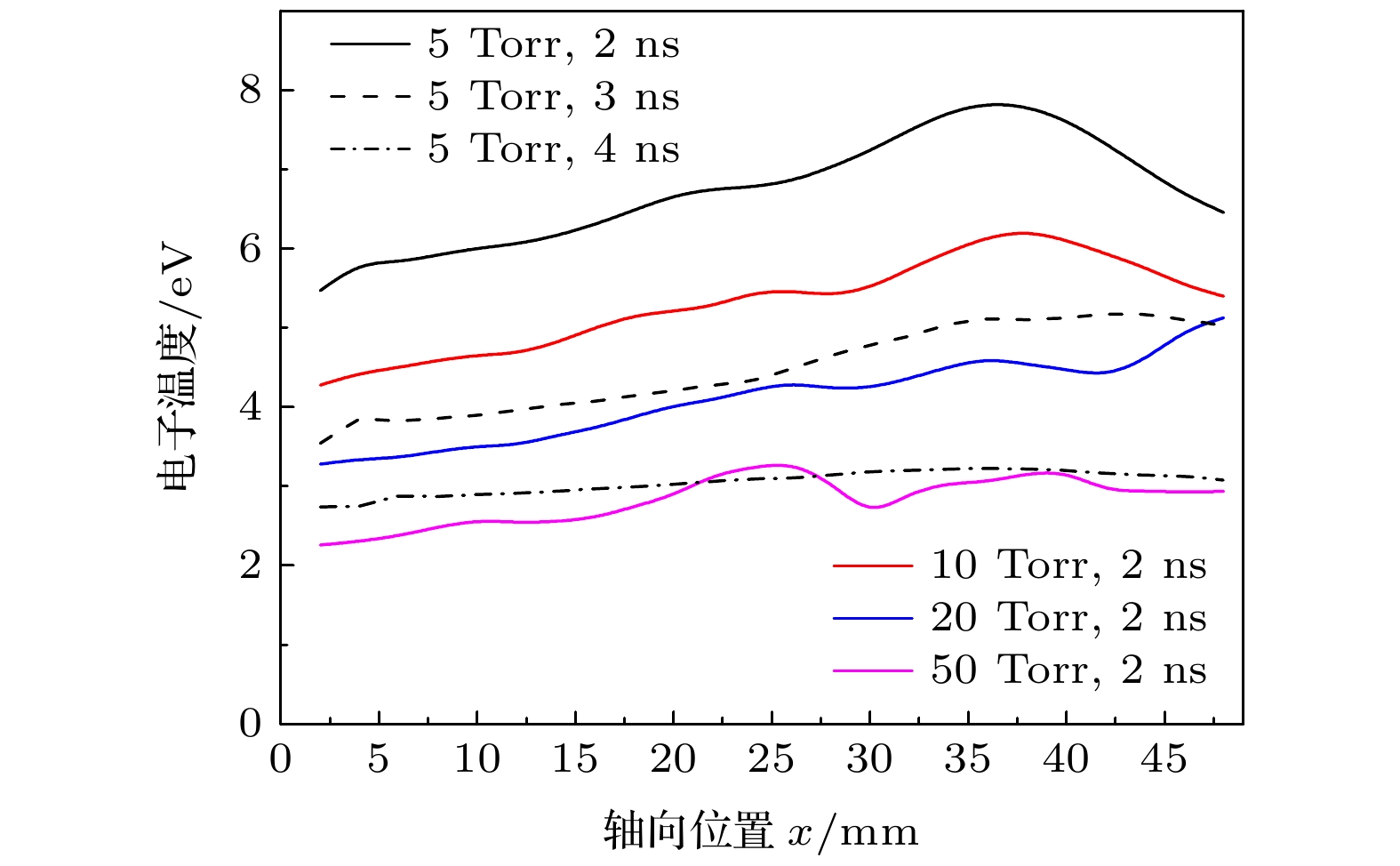
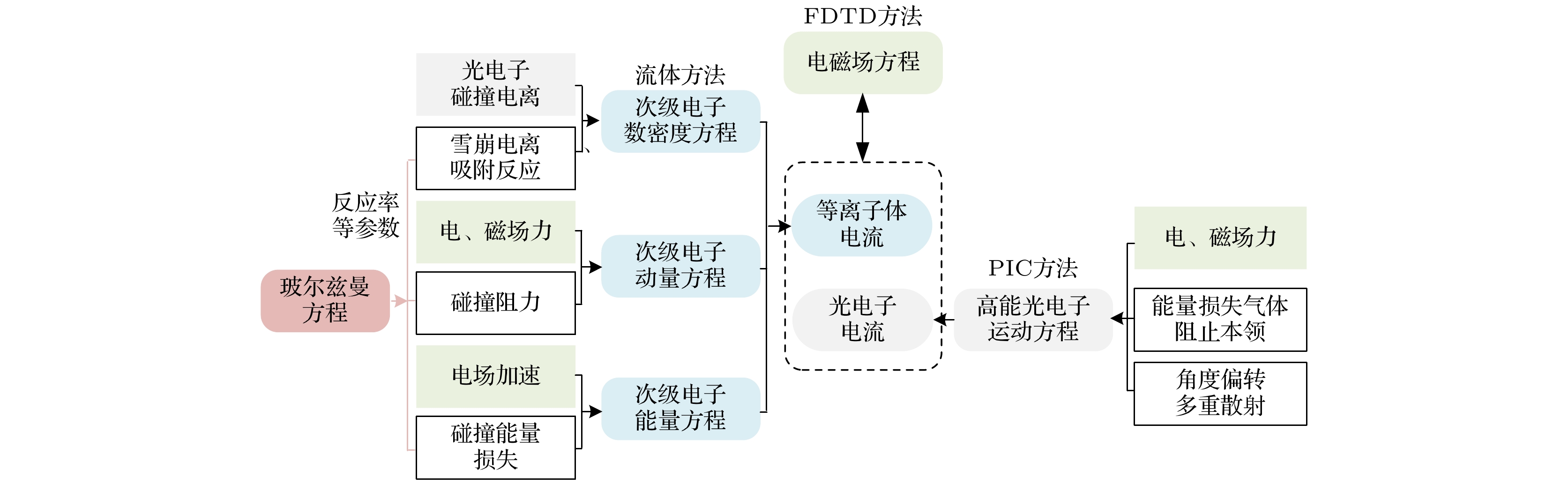
-
系统电磁脉冲广泛存在于强电离辐射环境中, 且难以有效屏蔽. 为了评估稀薄空气对系统电磁脉冲的影响, 本文基于粒子-流体混合模拟方法, 建立了三维非稳态模型, 计算并分析了稀薄空气等离子体的特性以及其与电磁场响应的相互作用. 结果表明, 压力越高, 光电子发射面附近的次级电子数密度越高, 轴向分布的梯度越大, 腔体中部的电子数密度在20 Torr (1 Torr = 133 Pa)下出现峰值, 而电子温度随压力升高单调递减. 腔体内的稀薄空气等离子体阻碍了空间电荷层的产生, 电场响应峰值比真空条件下的低了一个数量级, 电场脉冲宽度也显著降低. 光电子运动特性决定了电流响应的峰值, 压力升高, 到达腔体末端的电流先增加再减小. 而等离子体电流会抑制总电流的上升速率, 并使电流响应出现拖尾. 最后, 将数值模拟结果与电子束模拟系统电磁脉冲的实验结果进行比较, 验证了本文混合模拟模型的可靠性. 本研究所采用的混合模拟方法相比于粒子云网格-蒙特卡罗碰撞方法, 大幅减小了计算消耗.The surface of metal system exposed to ionizing radiation (X-ray and γ-ray) will emit high-energy electrons through the photoelectric effect and other processes. The transient electromagnetic field generated by the high-speed electron flow is called system generated electromagnetic pulse (SGEMP), which is difficult to shield effectively. An ongoing effort has been made to investigate the SGEMP response in vacuum by numerical simulation. However, the systems are usually operated in a gaseous environment. The objective of this paper is to investigate the effect of low-pressure air on the SGEMP. A three-dimensional hybrid simulation model is developed to calculate the characteristics of the electron beam induced air plasma and its interaction with the electromagnetic field. In the hybrid model, the high-energy photoelectrons are modelled as macroparticles, and secondary electrons are treaed as fluid for a balance between efficiency and accuracy. A cylindrical cavity with an inner diameter of 100 mm and a length of 50 mm is used. The photoelectrons are emitted from one end of the cavity and are assumed to be monoenergetic (20 keV). The photoelectron pulse follows a sine-squared distribution with a peak current density of 10 A/cm2, and its full width at half maximum is 2 ns. The results show that the number density of the secondary electrons near the photoelectron emission surface and its axial gradient increase as air pressure increases. The electron number density in the middle of the cavity shows a peak value at 20 Torr (1 Torr = 133 Pa). The electron temperature decreases monotonically with the increase in pressure. The low-pressure air plasma in the cavity prevents the space charge layer from being generated. The peak value of the electric field is an order of magnitude lower than that in vacuum, and the pulse width is also significantly reduced. The emission characteristic of the photoelectrons determines the peak value of the current response. The current reaching the end of the cavity surface first increases and then decreases with pressure increasing. The plasma return current can suppress the rising rate of the total current and extend the duration of current responses. Finally, to validate the established hybrid simulation model, the calculated magnetic field is compared with that from the benchmark experiments. This paper helps to achieve a better prediction of the SGEMP response in a gaseous environment. Compared with the particle-in-cell Monte Carlo collision method, the hybrid model adopted can greatly reduce the computational cost.
-
Keywords:
- system generated electromagnetic pulse (SGEMP) /
- photoelectrons /
- particle-in-cell simulation /
- hybrid modelling
[1] 王泰春, 贺云汉, 王玉芝 2011 电磁脉冲导论 (北京: 国防工业出版社) 第130页
Wang T C, He Y H, Wang Y Z 2011 Introduction to Electromagnetic Pulse (Beijing: National Defense Industry Press) p130 (in Chinese)
[2] 美国电磁脉冲袭击对美威胁评估委员会编 (郑毅, 梁睿, 曹保锋译 2019 电磁脉冲袭击对国家重要基础设施的影响 (北京: 科学出版社)第9页
Commission to assess the threat to the United States from electromagnetic pulse (EMP) attack (translated by Zheng Y, Liang R, Cao B F) 2019 Report of the Commission to Assess the Threat to the United States from Electromagnetic Pulse (EMP) attack: Critical National Infrastructures (Beijing: Science Press) p9
[3] Meng C, Xu Z Q, Jiang Y S, Zheng W G, Dang Z 2017 IEEE Trans. Nucl. Sci. 64 2618
Google Scholar
[4] Genuario R D 1975 IEEE Trans. Nucl. Sci. 22 2098
Google Scholar
[5] Swanekamp S B, Hinshelwood D, Angus J R, Richardson A S, Mosher D 2016 Direct Electron-Beam Injection Experiments for Validation of Air-Chemistry Models (Report)
[6] Ribière M, D’Almeida T, Cessenat O, Maulois M, Pouzalgues R, Crabos B, Delbos C, Garrigues A, Azaïs B 2016 Phys. Plasmas 23 122106
Google Scholar
[7] Woods A J, Delmer T N 1976 The arbitrary body of revolution code (ABORC) for SGEMP/IEMP (report)
[8] Xu Z Q, Meng C, Jiang Y S, Wu P 2020 IEEE Trans. Nucl. Sci. 67 425
Google Scholar
[9] Wang J G, Zhang D H, Liu C L, Li Y D, Wang Y, Wang H G, Qiao H L, Li X Z 2009 Phys. Plasmas 16 033108
Google Scholar
[10] Wang J G, Chen Z G, Wang Y, Zhang D H, Liu C L, Li Y D, Wang H G, Qiao H L, Fu M Y, Yuan Y 2010 Phys. Plasmas 17 073107
Google Scholar
[11] Wang Y, Wang J G, Chen Z G, Cheng G X, Wang P 2016 Comput. Phys. Commun. 205 1
Google Scholar
[12] Chen J N, Wang J G, Tao Y L, Chen Z G, Wang Y, Niu S L 2019 IEEE Trans. Nucl. Sci. 66 820
Google Scholar
[13] Chen J N, Wang J G, Chen Z G, Ren Z P 2020 IEEE Trans. Nucl. Sci. 67 818
Google Scholar
[14] Chen J H, Chao Z, Deng J H, Li Z D 2020 IEEE Trans. Nucl. Sci. 67 2353
Google Scholar
[15] 张含天, 周前红, 周海京, 孙强, 宋萌萌, 董烨, 杨薇, 姚建生 2021 70 165201
Google Scholar
Zhang H T, Zhou Q H, Zhou H J, Sun Q, Song M M, Dong Y, Yang W, Yao J S 2021 Acta Phys. Sin. 70 165201
Google Scholar
[16] 孙会芳, 张玲玉, 董志伟, 周海京 2019 强激光与粒子束 31 103221
Google Scholar
Sun H F, Zhang L Y, Dong Z W, Zhou H J 2019 High Power Laser and Particle Beams 31 103221
Google Scholar
[17] Gilbert R M, Klebers J, Bromborsky A 1977 IEEE Trans. Nucl. Sci. 24 2389
Google Scholar
[18] Woods A J, Hobbs W E, Wenaas E P 1981 IEEE Trans. Nucl. Sci. 28 4467
Google Scholar
[19] Longmire C T 1975 IEEE Trans. Nucl. Sci. 22 2340
Google Scholar
[20] Chan P C, Woods A J 1985 IEEE Trans. Nucl. Sci. 32 4441
Google Scholar
[21] Strasburg S, Hinshelwood D D, Schumer J W, Mosher D, Ottinger P F, Fernsler R F, Slinker S P 2003 Phys. Plasmas 10 3758
Google Scholar
[22] Pusateri E N, Morris H E, Nelson E M, Ji W 2015 J. Geophys. Res. Atmos. 120 7300
Google Scholar
[23] Angus J R, Mosher D, Swanekamp S B, Ottinger P F, Schumer J W, Hinshelwood D D 2016 Phys. Plasmas 23 053510
Google Scholar
[24] Ribière M, Cessenat O, D’Almeida T, De Gaufridy De Dortan F, Maulois M, Delbos C, Garrigues A, Azaïs B 2016 Phys. Plasmas 23 032105
Google Scholar
[25] Zhang H T, Zhou Q H, Zhou H J, Sun Q, Song M M, Dong Y, Yang W, Yao J S 2021 J. Appl. Phys. 130 173303
Google Scholar
[26] Wang J G, Cai L B, Zhu X Q, Wang Y, Xuan C 2010 Phys. Plasmas 17 063503
Google Scholar
[27] 李小泽, 王建国, 董长江, 张海 2008 57 4613
Google Scholar
Li X Z, Wang J G, Tong C J, Zhang H 2008 Acta Phys. Sin. 57 4613
Google Scholar
[28] Birdsall C K, Langdon A B 2004 Plasma Physics via Computer Simulation (Bristol: IOP Publishing Ltd) p228
[29] Pointon T D 2008 Comput. Phys. Commun. 179 535
Google Scholar
[30] Wang H Y, Jiang W, Sun P, Kong L B 2014 Chin. Phys. B 23 035204
Google Scholar
[31] Esirkepov T 2001 Comput. Phys. Commun. 135 144
Google Scholar
[32] Greenwood A D, Cartwright K L, Luginsland J W, Baca E A 2004 J. Comput. Phys. 201 665
Google Scholar
[33] 周辉, 程引会, 李宝忠, 陈雨生 2000 计算物理 17 121
Google Scholar
Zhou H, Cheng Y H, Li B Z, Chen Y S 2000 Chin. J. Comput. Phys. 17 121
Google Scholar
[34] 颜强 2017 博士学位论文 (哈尔滨: 哈尔滨工程大学) 第55页
Yan Q 2017 Ph. D. Dissertation (Harbin: Harbin Engineering University) p55 (in Chinese)
[35] Sugiyama H 1981 Radiat. Eff. Defects Solids 56 205
Google Scholar
[36] Sugiyama H 1985 Plasma Sources Sci. Technol. 30 331
Google Scholar
[37] Gümüş H 2005 Radiat. Phys. Chem. 72 7
Google Scholar
[38] Gümüş H 2008 Appl. Radiat. Isot. 66 1886
Google Scholar
[39] NIST ESTAR Database 2021 https://physics.nist.gov/Phys RefData/Star/Text/ESTAR.html [2021-8-1]
[40] Longmire C T, Longley H 1973 Improvements in the Treatment of Compton Current and Air Conductivity in EMP Problems (Report)
[41] Farmer W A, Cohen B I, Eng C D 2016 IEEE Trans. Nucl. Sci. 63 1259
Google Scholar
[42] Farmer W A, Friedman A 2015 IEEE Trans. Nucl. Sci. 62 1695
Google Scholar
[43] Robinson A P L, Strozzi D J, Davies J R, Gremillet L, Honrubia J J, Johzaki T, Kingham R J, Sherlock M, Solodov A A 2014 Nucl. Fusion 54 054003
Google Scholar
[44] Higgins D F, Longmire C L, O’Dell A A 1973 A Method for Estimating the X-Ray Produced Electromagnetic Pulse Observed in the Source Region of a High-Altitude Burst (report)
[45] Itikawa Y 2006 J. Phys. Chem. Ref. Data 35 31
Google Scholar
[46] Phelps Database www.lxcat.net/Phelps [2021-8-1]
[47] Rapp D, Englander-Golden P 1965 J. Chem. Phys. 43 1464
Google Scholar
[48] Kim Y K, Santos J P, Parente F 2000 Phys. Rev. A:At. Mol. Opt. Phys. 62 052710
Google Scholar
[49] Maulois M, Ribière M, Eichwald O, Yousfi M, Pouzalgues R, Garrigues A, Delbos C, Azaïs B 2016 Phys. Plasmas 23 102117
Google Scholar
[50] Gilbert J L, Radasky W A, Savage E B 2013 IEEE Trans. Electromagn. Compat. 55 446
Google Scholar
[51] Hagelaar G J M, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722
Google Scholar
[52] Wu Y, Zhang H T, Luo B, Yang F, Sun H, Li T W, Tang L 2017 Plasma Chem. Plasma Process. 37 1051
Google Scholar
[53] Forster R A, Cox L J, Barrett R F, Booth T E, Briesmeister J F, Brown F B, Bull J S, Geisler G C, Goorley J T, Mosteller R D, Post S E, Prael R E, Selcow E C, Sood A 2004 Nucl. Instrum. Methods Phys. Res., Sect. B 213 82
Google Scholar
[54] 陈剑楠, 陶应龙, 牛胜利 2020 现代应用物理 11 010501
Chen J N, Tao Y L, Niu S L 2020 Mod. Appl. Phys. 11 010501
[55] Pointon T D, Cartwright K L 2014 Proceedings of the 67th APS Gaseous Electronics Conference Raleigh NC, USA, November 2–7, 2014 p00051
[56] Maulois M, Ribière M, Eichwald O, Yousfi M, Pouzalgues R, Garrigues A, Delbos C, Azaïs B 2016 J. Appl. Phys. 120 123302
Google Scholar
[57] 宋法伦, 张永辉, 向飞, 常安碧 2008 57 1807
Google Scholar
Song F L, Zhang Y H, Xiang F, Chang A B 2008 Acta Phys. Sin. 57 1807
Google Scholar
-
图 4 约化swarm参数随电子能量的变化
Fig. 4. Normalized swarm parameters as a function of electron energy.
图 6 光电子与次级电子的分布(0—20 Torr, 1—4 ns)
Fig. 6. Distributions of photoelectrons (red dot) and secondary electrons (0–20 Torr, 1–4 ns)
图 7 真空(a)以及10 Torr压力(b)下, 轴向电场Ex随时间的变化(x = 2, 10, 40 mm; r = 0 mm)
Fig. 7. Time-dependent electric field Ex (x = 2, 10, 40 mm; r = 0 mm) for (a) vacuum and (b) 10 Torr.
图 8 不同压力下, 切向磁感应强度Bφ随时间的变化(x = 48 mm; r = 48 mm)
Fig. 8. Time-dependent magnetic flux density Bφ at different pressures (x = 48 mm; r = 48 mm).
图 9 截面上光电子、次级电子电流随时间的变化(10 Torr) (a) x = 10 mm; (b) x = 40 mm
Fig. 9. Time-dependent current of photoelectrons and secondary electrons (10 Torr) for the plane: (a) x = 10 mm; (b) x = 40 mm.
图 10 不同压力下, 对称轴上次级电子数密度的分布(r = 0 mm, t = 2 ns)
Fig. 10. Distributions of secondary electrons along the axis at different pressures (r = 10 mm, t = 2 ns).
图 11 不同压力下, x = 24 mm处次级电子数密度的径向线积分随时间的变化
Fig. 11. Line-integrated secondary electrons at x = 24 mm at different pressures.
图 12 对称轴上的次级电子温度分布(r = 0 mm)
Fig. 12. Distributions of secondary electron temperature along the axis (r = 0 mm).
图 13 实验中电子束电流(左)与电子能量(右)随时间的关系
Fig. 13. Electron beam current (left) and energy (right) as functions of time.
图 14 Z = 12.5 cm, r = 13.8 cm处的磁场强度(腔体内压力3 Torr)
Fig. 14. Magnetic field at Z = 12.5 cm, r = 13.8 cm for an air pressure of 3 Torr
-
[1] 王泰春, 贺云汉, 王玉芝 2011 电磁脉冲导论 (北京: 国防工业出版社) 第130页
Wang T C, He Y H, Wang Y Z 2011 Introduction to Electromagnetic Pulse (Beijing: National Defense Industry Press) p130 (in Chinese)
[2] 美国电磁脉冲袭击对美威胁评估委员会编 (郑毅, 梁睿, 曹保锋译 2019 电磁脉冲袭击对国家重要基础设施的影响 (北京: 科学出版社)第9页
Commission to assess the threat to the United States from electromagnetic pulse (EMP) attack (translated by Zheng Y, Liang R, Cao B F) 2019 Report of the Commission to Assess the Threat to the United States from Electromagnetic Pulse (EMP) attack: Critical National Infrastructures (Beijing: Science Press) p9
[3] Meng C, Xu Z Q, Jiang Y S, Zheng W G, Dang Z 2017 IEEE Trans. Nucl. Sci. 64 2618
Google Scholar
[4] Genuario R D 1975 IEEE Trans. Nucl. Sci. 22 2098
Google Scholar
[5] Swanekamp S B, Hinshelwood D, Angus J R, Richardson A S, Mosher D 2016 Direct Electron-Beam Injection Experiments for Validation of Air-Chemistry Models (Report)
[6] Ribière M, D’Almeida T, Cessenat O, Maulois M, Pouzalgues R, Crabos B, Delbos C, Garrigues A, Azaïs B 2016 Phys. Plasmas 23 122106
Google Scholar
[7] Woods A J, Delmer T N 1976 The arbitrary body of revolution code (ABORC) for SGEMP/IEMP (report)
[8] Xu Z Q, Meng C, Jiang Y S, Wu P 2020 IEEE Trans. Nucl. Sci. 67 425
Google Scholar
[9] Wang J G, Zhang D H, Liu C L, Li Y D, Wang Y, Wang H G, Qiao H L, Li X Z 2009 Phys. Plasmas 16 033108
Google Scholar
[10] Wang J G, Chen Z G, Wang Y, Zhang D H, Liu C L, Li Y D, Wang H G, Qiao H L, Fu M Y, Yuan Y 2010 Phys. Plasmas 17 073107
Google Scholar
[11] Wang Y, Wang J G, Chen Z G, Cheng G X, Wang P 2016 Comput. Phys. Commun. 205 1
Google Scholar
[12] Chen J N, Wang J G, Tao Y L, Chen Z G, Wang Y, Niu S L 2019 IEEE Trans. Nucl. Sci. 66 820
Google Scholar
[13] Chen J N, Wang J G, Chen Z G, Ren Z P 2020 IEEE Trans. Nucl. Sci. 67 818
Google Scholar
[14] Chen J H, Chao Z, Deng J H, Li Z D 2020 IEEE Trans. Nucl. Sci. 67 2353
Google Scholar
[15] 张含天, 周前红, 周海京, 孙强, 宋萌萌, 董烨, 杨薇, 姚建生 2021 70 165201
Google Scholar
Zhang H T, Zhou Q H, Zhou H J, Sun Q, Song M M, Dong Y, Yang W, Yao J S 2021 Acta Phys. Sin. 70 165201
Google Scholar
[16] 孙会芳, 张玲玉, 董志伟, 周海京 2019 强激光与粒子束 31 103221
Google Scholar
Sun H F, Zhang L Y, Dong Z W, Zhou H J 2019 High Power Laser and Particle Beams 31 103221
Google Scholar
[17] Gilbert R M, Klebers J, Bromborsky A 1977 IEEE Trans. Nucl. Sci. 24 2389
Google Scholar
[18] Woods A J, Hobbs W E, Wenaas E P 1981 IEEE Trans. Nucl. Sci. 28 4467
Google Scholar
[19] Longmire C T 1975 IEEE Trans. Nucl. Sci. 22 2340
Google Scholar
[20] Chan P C, Woods A J 1985 IEEE Trans. Nucl. Sci. 32 4441
Google Scholar
[21] Strasburg S, Hinshelwood D D, Schumer J W, Mosher D, Ottinger P F, Fernsler R F, Slinker S P 2003 Phys. Plasmas 10 3758
Google Scholar
[22] Pusateri E N, Morris H E, Nelson E M, Ji W 2015 J. Geophys. Res. Atmos. 120 7300
Google Scholar
[23] Angus J R, Mosher D, Swanekamp S B, Ottinger P F, Schumer J W, Hinshelwood D D 2016 Phys. Plasmas 23 053510
Google Scholar
[24] Ribière M, Cessenat O, D’Almeida T, De Gaufridy De Dortan F, Maulois M, Delbos C, Garrigues A, Azaïs B 2016 Phys. Plasmas 23 032105
Google Scholar
[25] Zhang H T, Zhou Q H, Zhou H J, Sun Q, Song M M, Dong Y, Yang W, Yao J S 2021 J. Appl. Phys. 130 173303
Google Scholar
[26] Wang J G, Cai L B, Zhu X Q, Wang Y, Xuan C 2010 Phys. Plasmas 17 063503
Google Scholar
[27] 李小泽, 王建国, 董长江, 张海 2008 57 4613
Google Scholar
Li X Z, Wang J G, Tong C J, Zhang H 2008 Acta Phys. Sin. 57 4613
Google Scholar
[28] Birdsall C K, Langdon A B 2004 Plasma Physics via Computer Simulation (Bristol: IOP Publishing Ltd) p228
[29] Pointon T D 2008 Comput. Phys. Commun. 179 535
Google Scholar
[30] Wang H Y, Jiang W, Sun P, Kong L B 2014 Chin. Phys. B 23 035204
Google Scholar
[31] Esirkepov T 2001 Comput. Phys. Commun. 135 144
Google Scholar
[32] Greenwood A D, Cartwright K L, Luginsland J W, Baca E A 2004 J. Comput. Phys. 201 665
Google Scholar
[33] 周辉, 程引会, 李宝忠, 陈雨生 2000 计算物理 17 121
Google Scholar
Zhou H, Cheng Y H, Li B Z, Chen Y S 2000 Chin. J. Comput. Phys. 17 121
Google Scholar
[34] 颜强 2017 博士学位论文 (哈尔滨: 哈尔滨工程大学) 第55页
Yan Q 2017 Ph. D. Dissertation (Harbin: Harbin Engineering University) p55 (in Chinese)
[35] Sugiyama H 1981 Radiat. Eff. Defects Solids 56 205
Google Scholar
[36] Sugiyama H 1985 Plasma Sources Sci. Technol. 30 331
Google Scholar
[37] Gümüş H 2005 Radiat. Phys. Chem. 72 7
Google Scholar
[38] Gümüş H 2008 Appl. Radiat. Isot. 66 1886
Google Scholar
[39] NIST ESTAR Database 2021 https://physics.nist.gov/Phys RefData/Star/Text/ESTAR.html [2021-8-1]
[40] Longmire C T, Longley H 1973 Improvements in the Treatment of Compton Current and Air Conductivity in EMP Problems (Report)
[41] Farmer W A, Cohen B I, Eng C D 2016 IEEE Trans. Nucl. Sci. 63 1259
Google Scholar
[42] Farmer W A, Friedman A 2015 IEEE Trans. Nucl. Sci. 62 1695
Google Scholar
[43] Robinson A P L, Strozzi D J, Davies J R, Gremillet L, Honrubia J J, Johzaki T, Kingham R J, Sherlock M, Solodov A A 2014 Nucl. Fusion 54 054003
Google Scholar
[44] Higgins D F, Longmire C L, O’Dell A A 1973 A Method for Estimating the X-Ray Produced Electromagnetic Pulse Observed in the Source Region of a High-Altitude Burst (report)
[45] Itikawa Y 2006 J. Phys. Chem. Ref. Data 35 31
Google Scholar
[46] Phelps Database www.lxcat.net/Phelps [2021-8-1]
[47] Rapp D, Englander-Golden P 1965 J. Chem. Phys. 43 1464
Google Scholar
[48] Kim Y K, Santos J P, Parente F 2000 Phys. Rev. A:At. Mol. Opt. Phys. 62 052710
Google Scholar
[49] Maulois M, Ribière M, Eichwald O, Yousfi M, Pouzalgues R, Garrigues A, Delbos C, Azaïs B 2016 Phys. Plasmas 23 102117
Google Scholar
[50] Gilbert J L, Radasky W A, Savage E B 2013 IEEE Trans. Electromagn. Compat. 55 446
Google Scholar
[51] Hagelaar G J M, Pitchford L C 2005 Plasma Sources Sci. Technol. 14 722
Google Scholar
[52] Wu Y, Zhang H T, Luo B, Yang F, Sun H, Li T W, Tang L 2017 Plasma Chem. Plasma Process. 37 1051
Google Scholar
[53] Forster R A, Cox L J, Barrett R F, Booth T E, Briesmeister J F, Brown F B, Bull J S, Geisler G C, Goorley J T, Mosteller R D, Post S E, Prael R E, Selcow E C, Sood A 2004 Nucl. Instrum. Methods Phys. Res., Sect. B 213 82
Google Scholar
[54] 陈剑楠, 陶应龙, 牛胜利 2020 现代应用物理 11 010501
Chen J N, Tao Y L, Niu S L 2020 Mod. Appl. Phys. 11 010501
[55] Pointon T D, Cartwright K L 2014 Proceedings of the 67th APS Gaseous Electronics Conference Raleigh NC, USA, November 2–7, 2014 p00051
[56] Maulois M, Ribière M, Eichwald O, Yousfi M, Pouzalgues R, Garrigues A, Delbos C, Azaïs B 2016 J. Appl. Phys. 120 123302
Google Scholar
[57] 宋法伦, 张永辉, 向飞, 常安碧 2008 57 1807
Google Scholar
Song F L, Zhang Y H, Xiang F, Chang A B 2008 Acta Phys. Sin. 57 1807
Google Scholar
下载:
计量
- 文章访问数: 4151
- PDF下载量: 68
- 被引次数: 0
