-
基于包含驱动和阻尼的三波非线性相互作用模型, 构建了一个描述高能量粒子测地声模(EGAM)与Dimits区漂移波湍流相互作用的系统, 并在系统的线性增长及非线性振荡阶段分别进行了解析和数值研究. 更进一步的数值结果表明, 在忽略EGAM的贡献时, 该系统具有随着线性驱动/阻尼率等参数的变化, 从极限环振荡经历倍周期分岔最终进入混沌的行为特征.在此基础上, 形式上构建了本系统的非线性饱和Dimits区, 并研究了EGAM对Dimits区漂移波的影响. 结果表明, 对于不同幅度和频率的EGAM, 被调制后的漂移波将表现出受到激发或抑制的效果. 对此, 采用相空间分析的方法给出了相应的解释.Based on the nonlinear three-wave interaction model including driving and dissipation, we construct a system to describe the nonlinear interaction between energetic particle induced geodesic acoustic mode (EGAM) and the drift waves turbulence in the Dimits shift region, and study both analytically and numerically the linear growth and nonlinear oscillation phases of the system, respectively. Further numerical results show that, without the contribution of EGAM, the system goes through limited cycle oscillation to period doubling, and finally route to chaos with the change of the linear drive/dissipation rate. On this basis, the nonlinear saturated “Dimits region” of the system is constructed, which is then used to study the influence of EGAM on the drift wave in the Dimits region. The results show that for EGAM with different amplitude and frequency, the modulated drift wave can be either excited or suppressed, partly reproduces the results from large scale simulation. Finally, We use the method of phase space analysis to give the corresponding explanation.
-
Keywords:
- drift wave /
- zonal flow /
- EGAM /
- three-wave nonlinear coupling
[1] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[2] Artsimovich L A, Bobrovskii G A, Mirnov S A, Razumova K A, Strelkov V S 1967 Sov. At. Energy 22 325
[3] Chen L 1999 J. Geophys. Res. Space Phys. 104 2421
Google Scholar
[4] Dimits A M, Bateman G, Beer M A, Cohen B I, Dorland W, Hammett G W, Kim C, Kinsey J E, Kotschenreuther M, Kritz A H, Lao L L, Mandrekas J, Nevins W M, Parker S E, Redd A J, Shumaker D E, Sydora R, Weiland J 2000 Phys. Plasmas 7 969
Google Scholar
[5] Lin Z, Hahm T S, Lee W W, Tang W M, White R B 1998 Science 281 1835
Google Scholar
[6] Chen L, Lin Z, White R 2000 Physics of Plasmas 7 3129
Google Scholar
[7] Diamond P H, Itoh S I, Itoh K, Hahm T S 2005 Plasma Phys. Controlled Fusion 47 R35
Google Scholar
[8] Rosenbluth M N, Hinton F L 1998 Phys. Rev. Lett. 80 724
Google Scholar
[9] Winsor N, Johnson J L, Dawson J M 1968 Phys. Fluids 11 2448
Google Scholar
[10] Zonca F, Chen L 2008 Europhys. Lett. 83 35001
Google Scholar
[11] Nazikian R, Fu G Y, Austin M E, Berk H L, Budny R V, Gorelenkov N N, Heidbrink W W, Holcomb C T, Kramer G J, McKee G R, Makowski M A, Solomon W M, Shafer M, Strait E J, Zeeland M A V 2008 Phys. Rev. Lett. 101 185001
Google Scholar
[12] Fu G 2008 Phys. Rev. Lett. 101 185002
Google Scholar
[13] Berk H, Zhou T 2010 Nuclear Fusion 50 035007
Google Scholar
[14] Qiu Z, Zonca F, Chen L 2010 Plasma Phys. Controlled Fusion 52 095003
Google Scholar
[15] Qiu Z, Chen L, Zonca F 2018 Plasma Sci. Technol. 20 094004
Google Scholar
[16] Zarzoso D, Sarazin Y, Garbet X, Dumont R, Strugarek A, Abiteboul J, Cartier-Michaud T, Dif-Pradalier G, Ghendrih P, Grandgirard V, Latu G, Passeron C, Thomine O 2013 Phys. Rev. Lett. 110 125002
Google Scholar
[17] Chen N F, Hu H, Zhang X, Wei S, Qiu Z 2021 Physics of Plasmas 28 042505
Google Scholar
[18] Qiu Z, Chen L, Zonca F 2014 Phys. Plasmas 21 022304
Google Scholar
[19] Zonca F, White R B, Chen L 2004 Phys. Plasmas 11 2488
Google Scholar
[20] Guo Z, Chen L, Zonca F 2009 Phys. Rev. Lett. 103 055002
Google Scholar
[21] Wersinger J M, Finn J M, Ott E 1980 Phys. Fluids 23 1142
Google Scholar
[22] Sagdeev R, Galeev A 1969 Nonlinear Plasma Theory (AW Benjamin Inc.)
[23] Edelstein D C, Wachman E S, Tang C L 1989 Appl. Phys. Lett. 54 1728
Google Scholar
[24] Hughes D W, Proctor M R E 1992 J. Fluid Mech. 244 583
[25] Anderson D, Bondeson A 1977 Phys. Fluids 20 1072
Google Scholar
[26] Manley J M, Rowe H E 1956 Proc. IRE 44 904
Google Scholar
[27] Chen N, Wei S, Wei G, Qiu Z 2022 Plasma Phys. Controlled Fusion 64 015503
Google Scholar
-
图 1 忽略3支波的线性增长/阻尼时, 3支波强度随时间的演化. 红色实线、蓝色虚线和黑色点线分别代表泵浦波、边带模和ZFZF的演化曲线
Fig. 1. Evolution of the strength of the three waves with time when the linear growth/damping of the three waves is ignored. Red solid line, blue dashed line and black dotted line represent the evolution curve of pump wave, sideband and ZFZF, respectively
图 2 (a)
$ \gamma_1/\gamma_0 $ 和$ \gamma_{\rm{Z}}/\gamma_0 $ 的参数空间内, 当参数取值在黄色区域(标记为U)时, 系统无限增长, 当参数取值在蓝色区域(标记为S)时, 系统稳定在有限范围内; (b), (c)两种情形下3个波的时间演化曲线Fig. 2. (a) In the parameter space of
$ \gamma_1/\gamma_0 $ and$ \gamma_{\rm{Z}}/\gamma_0 $ , when the parameter value is set in the yellow region (marked by U), the system grows infinitely, while in the blue region (marked by S), a stable state of the system is obtained; (b), (c) time evolution curves of the three waves in these two cases
图 3 (a)
$ \gamma_1/\gamma_0 = 5.0 $ ,$ \gamma_{\rm{Z}}/\gamma_0 = 5.5 $ 时泵浦波$ |\phi_0 | $ 随时间的演化; (b)$ \gamma_1/\gamma_0 = 5.0 $ ,$ \gamma_{\rm{Z}}/\gamma_0 = 5.8 $ 时泵浦波$ |\phi_0 | $ 随时间的演化; (c)$ z_n = \max{\{|\phi_0(t)|\}} $ 随$ \gamma_{\rm{Z}}/\gamma_0 $ 变化的散点图Fig. 3. (a) Time evolution curves of pump wave
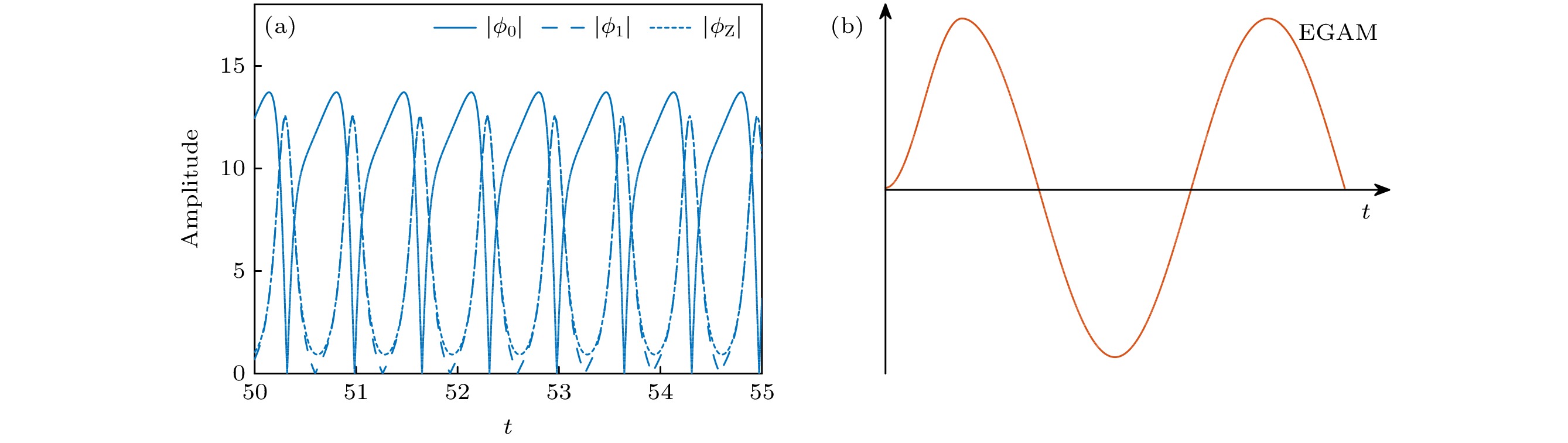
$ |\phi_0 | $ when$ \gamma_1/\gamma_0 = 5.0 $ ,$ \gamma_{\rm{Z}}/\gamma_0 = 5.5 $ ; (b) time evolution curves of pump wave$ |\phi_0 | $ when$ \gamma_1/\gamma_0 = 5.0 $ ,$ \gamma_{\rm{Z}}/\gamma_0 = 5.8 $ ; (c) scatter plot of$ z_n = \max{\{|\phi_0(t)|\}} $ varying with$ \gamma_{\rm{Z}}/\gamma_0 $ 
图 4 (a) 加入EGAM之前系统的周期性振荡. 蓝色实线、蓝色虚线和蓝色点线分别代表泵浦波、边带模和ZFZF和的时间演化曲线. (b) 周期振荡的EGAM曲线, 初始阶段逐步增强以实现平滑过渡
Fig. 4. (a) Periodic oscillation of the system before EGAM is introduced. The blue solid line, blue dashed line and blue dotted line represent the evolution curve of pump wave, sideband and ZFZF, respectively. (b) Periodically oscillating EGAM. The initial phase is progressively enhanced to achieve a smooth transition.
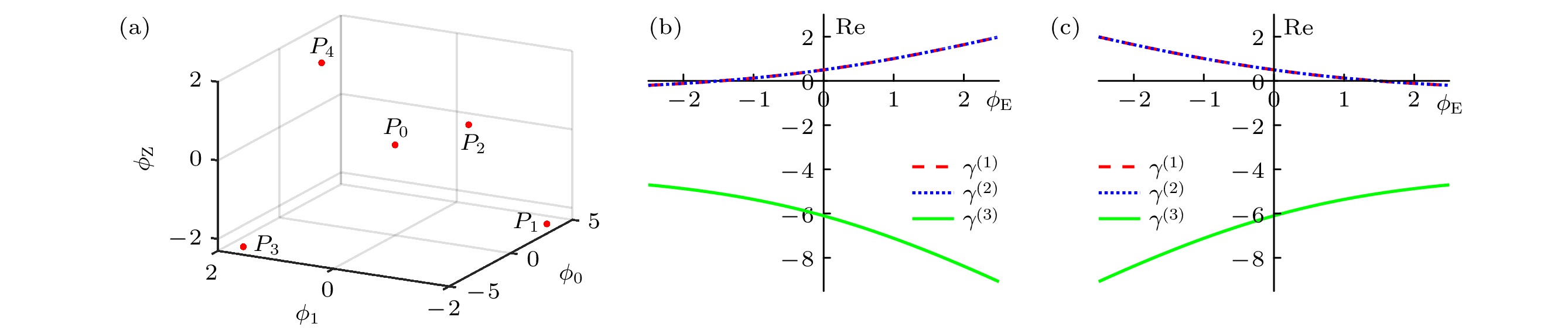
图 5 (a) 5个不动点在相空间的相对分布; (b) 不动点
$ P_1 $ 和$ P_3 $ , (c) 不动点$ P_2 $ 和$ P_4 $ 处Jacobi矩阵的3个本征值的实部随$ \phi_{\rm{E}} $ 的变化. 此处$ \gamma_0 = 1.0 $ ,$ \gamma_1 = 3.0 $ ,$ \gamma_{\rm{Z}} = 3.1 $ Fig. 5. (a) Relative distribution of five fixed points in phase space. Dependence of the real part of the three eigenvalues of Jacobi matrix at fixed points (b)
$ P_1 $ /$ P_3 $ and (c)$ P_2 $ /$ P_4 $ . Here,$ \gamma_0 = 1.0 $ ,$ \gamma_1 = 3.0 $ ,$ \gamma_{\rm{Z}} = 3.1 $ 
图 6 (a)
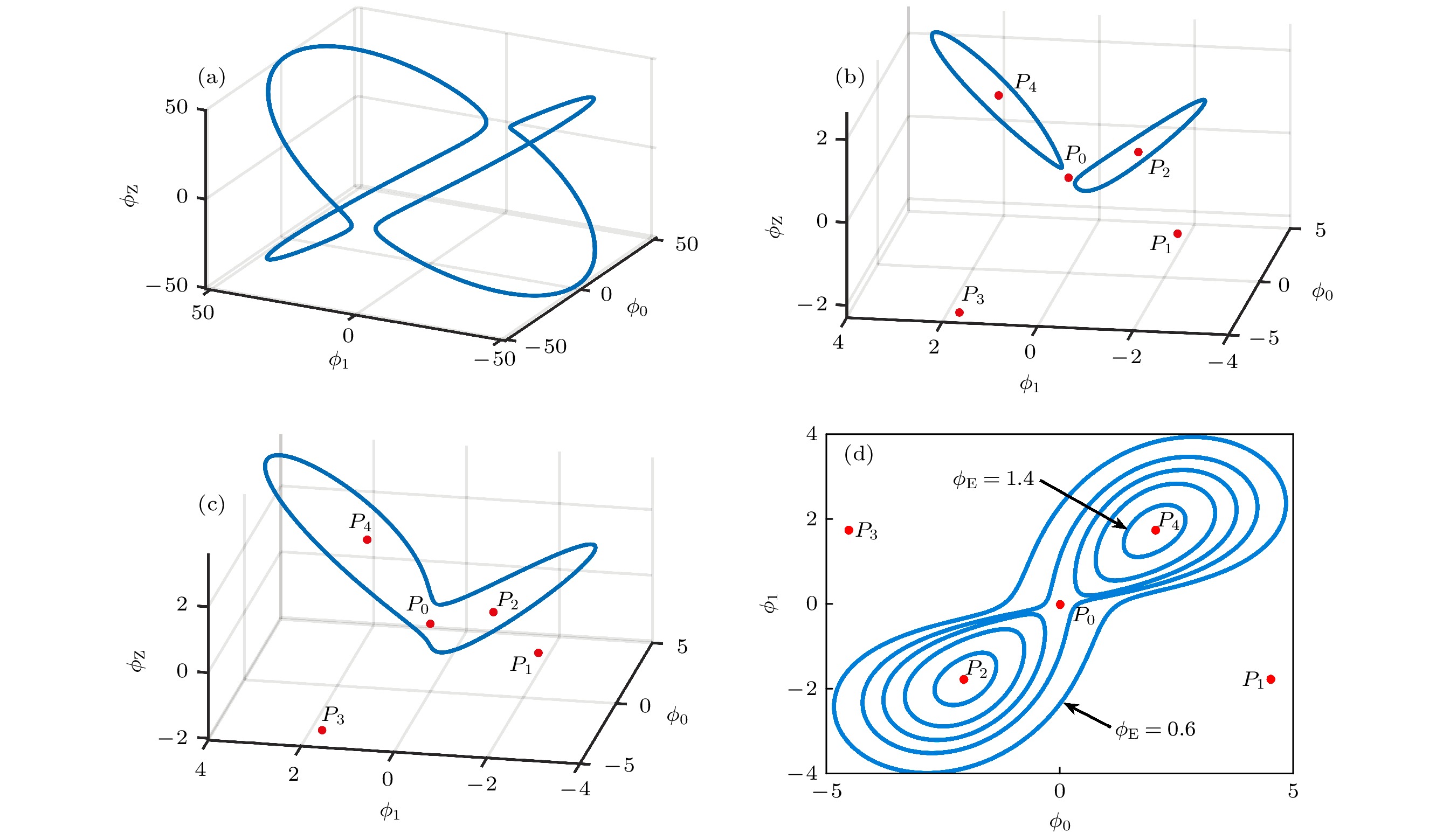
$ \phi_{\rm{E}} = 2.0 $ 时的大极限环; (b)$ \phi_{\rm{E}} = 1.0 $ 时的小极限环; (c)$ \phi_{\rm{E }}= 0.6 $ 时的中等尺寸极限环; (d)$ \phi_{\rm{E}} $ 从1.4减小到0.6, 两个小极限环合并为中等尺寸极限环的过程Fig. 6. (a) Big limit cycle when
$ \phi_{\rm{E}} = 2.0 $ ; (b) small limit cycle when$ \phi_{\rm{E}} = 1.0 $ ; (c) medium size limit cycle when$ \phi_{\rm{E}} = 0.6 $ ; (d) two small limit cycles combine into one medium size limit cycle with$ \phi_{\rm{E}} $ decreasing from 1.4 to 0.6
图 7 (a)
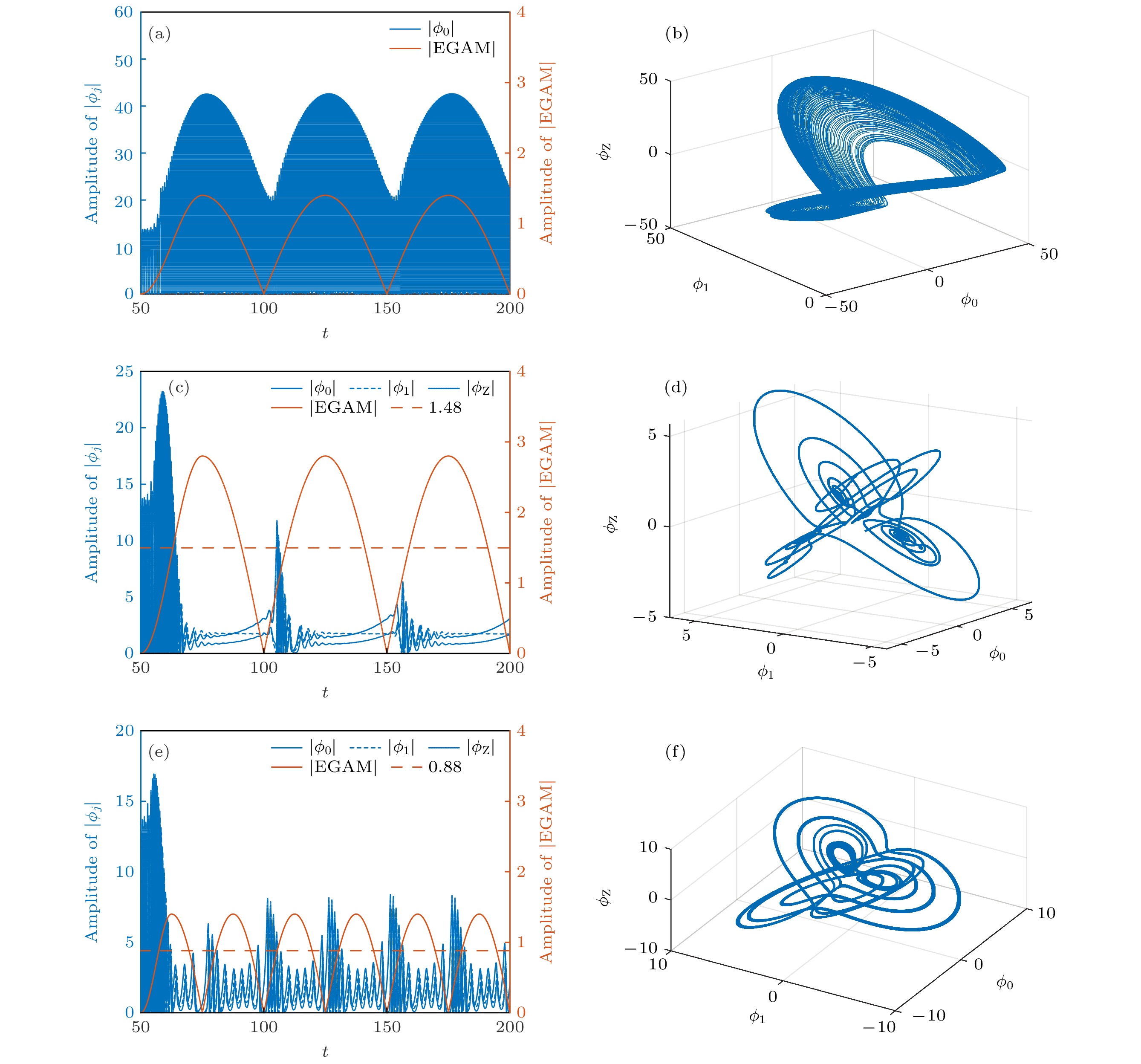
$ \phi_{\rm{E}} = 1.4 $ ,$ \omega_{\rm{E}} = 0.02\pi $ 时泵浦波$ |\phi_0 | $ 随时间的演化及(b)相应的相空间轨迹. (c)$ \phi_{\rm{E}} = 2.8 $ ,$ \omega_{\rm{E}} = 0.02\pi $ 时三波随时间的演化及(d) 相应的相空间轨迹. (e)$ \phi_{\rm{E}} = 1.4 $ ,$ \omega_{\rm{E}} = 0.04\pi $ 时三波随时间的演化及(f) 相应的相空间轨迹Fig. 7. (a) Time evolution of pump wave
$ |\phi_0 | $ when$ \phi_{\rm{E}} = 1.4 $ ,$ \omega_{\rm{E}} = 0.02\pi $ and (b) corresponding trajectory in phase space. (c) Time evolution of three waves when$ \phi_{\rm{E}} = 2.8 $ ,$ \omega_{\rm{E}} = 0.02\pi $ and (d) corresponding trajectory in phase space. (e) Time evolution of three waves when$ \phi_{\rm{E}} = 1.4 $ ,$ \omega_{\rm{E}} = 0.04\pi $ and (f) corresponding trajectory in phase space. -
[1] Horton W 1999 Rev. Mod. Phys. 71 735
Google Scholar
[2] Artsimovich L A, Bobrovskii G A, Mirnov S A, Razumova K A, Strelkov V S 1967 Sov. At. Energy 22 325
[3] Chen L 1999 J. Geophys. Res. Space Phys. 104 2421
Google Scholar
[4] Dimits A M, Bateman G, Beer M A, Cohen B I, Dorland W, Hammett G W, Kim C, Kinsey J E, Kotschenreuther M, Kritz A H, Lao L L, Mandrekas J, Nevins W M, Parker S E, Redd A J, Shumaker D E, Sydora R, Weiland J 2000 Phys. Plasmas 7 969
Google Scholar
[5] Lin Z, Hahm T S, Lee W W, Tang W M, White R B 1998 Science 281 1835
Google Scholar
[6] Chen L, Lin Z, White R 2000 Physics of Plasmas 7 3129
Google Scholar
[7] Diamond P H, Itoh S I, Itoh K, Hahm T S 2005 Plasma Phys. Controlled Fusion 47 R35
Google Scholar
[8] Rosenbluth M N, Hinton F L 1998 Phys. Rev. Lett. 80 724
Google Scholar
[9] Winsor N, Johnson J L, Dawson J M 1968 Phys. Fluids 11 2448
Google Scholar
[10] Zonca F, Chen L 2008 Europhys. Lett. 83 35001
Google Scholar
[11] Nazikian R, Fu G Y, Austin M E, Berk H L, Budny R V, Gorelenkov N N, Heidbrink W W, Holcomb C T, Kramer G J, McKee G R, Makowski M A, Solomon W M, Shafer M, Strait E J, Zeeland M A V 2008 Phys. Rev. Lett. 101 185001
Google Scholar
[12] Fu G 2008 Phys. Rev. Lett. 101 185002
Google Scholar
[13] Berk H, Zhou T 2010 Nuclear Fusion 50 035007
Google Scholar
[14] Qiu Z, Zonca F, Chen L 2010 Plasma Phys. Controlled Fusion 52 095003
Google Scholar
[15] Qiu Z, Chen L, Zonca F 2018 Plasma Sci. Technol. 20 094004
Google Scholar
[16] Zarzoso D, Sarazin Y, Garbet X, Dumont R, Strugarek A, Abiteboul J, Cartier-Michaud T, Dif-Pradalier G, Ghendrih P, Grandgirard V, Latu G, Passeron C, Thomine O 2013 Phys. Rev. Lett. 110 125002
Google Scholar
[17] Chen N F, Hu H, Zhang X, Wei S, Qiu Z 2021 Physics of Plasmas 28 042505
Google Scholar
[18] Qiu Z, Chen L, Zonca F 2014 Phys. Plasmas 21 022304
Google Scholar
[19] Zonca F, White R B, Chen L 2004 Phys. Plasmas 11 2488
Google Scholar
[20] Guo Z, Chen L, Zonca F 2009 Phys. Rev. Lett. 103 055002
Google Scholar
[21] Wersinger J M, Finn J M, Ott E 1980 Phys. Fluids 23 1142
Google Scholar
[22] Sagdeev R, Galeev A 1969 Nonlinear Plasma Theory (AW Benjamin Inc.)
[23] Edelstein D C, Wachman E S, Tang C L 1989 Appl. Phys. Lett. 54 1728
Google Scholar
[24] Hughes D W, Proctor M R E 1992 J. Fluid Mech. 244 583
[25] Anderson D, Bondeson A 1977 Phys. Fluids 20 1072
Google Scholar
[26] Manley J M, Rowe H E 1956 Proc. IRE 44 904
Google Scholar
[27] Chen N, Wei S, Wei G, Qiu Z 2022 Plasma Phys. Controlled Fusion 64 015503
Google Scholar
下载:
计量
- 文章访问数: 4512
- PDF下载量: 80
- 被引次数: 0
