-
利用新提出的Gilmore-NASG模型, 在考虑液体可压缩效应的边界条件下, 研究了可压缩液体中气泡的声空化特性, 并与利用原有KM-VdW模型计算得到的结果进行了比较. 结果表明, 相比于KM-VdW模型, 由于Gilmore-NASG模型采用新的状态方程来描述气体、液体以及由可压缩性引起的液体密度变化及声速变化, 所以用Gilmore-NASG模型得到的空化气泡的压缩比更大、崩溃深度更深、温度和压力峰值更高. 随着驱动声压幅值的增大, 两种模型给出的结果差别愈加明显, 而随着驱动频率的增大, 两种模型给出的结果差别逐渐减小. 这表明, 在充分考虑泡内气体、周围液体在不同温度和压强下共体积的变化所导致的介质可压缩特性下, 气泡内的温度和压强可能达到更高值. 同时, Gilmore-NASG模型还预测出了气泡壁处液体的密度变化、压力变化、温度变化以及液体中的声速变化. 因此, Gilmore-NASG模型在研究高压状态下气泡的空化特性以及周围液体对气泡空化特性的影响方面具有优点.The newly proposed Gilmore-NASG model is used to study the acoustic cavitation characteristics of bubble in compressible liquid under the boundary condition of considering the compressible effect of the liquid, and comparison is made between the results calculated by the Gilmore-NASG model and original KM-VdW model without considering the mass exchange, chemical reaction and heat exchange between the gas in the bubble and the surrounding liquid. The results suggest that, compared with the KM-VdW model, the Gilmore-NASG model which employs a new equation of state to describe the gas, liquid and variations of liquid density and sound velocity due to compressibility, can give a larger compression ratio of cavitation bubble, a deeper collapse depth, higher temperature and pressure peaks. This is mainly because that the co-volume of argon molecule in the NASG equation of state is smaller than that in the VdW equation of state and the effect of the co-volume of water molecule is considered in the NASG equation of state, that is, the Gilmore-NASG model gives more comprehensive consideration to the liquid compressibility. When the bubble collapses violently, the Gilmore-NASG model takes into account the changes of sound velocity caused by the compressibility of the liquid at the bubble wall, effectively avoid the possibility of abnormal increase in the Mach number of the liquid at the bubble wall. With the increase in the driving sound pressure amplitude, the difference between the results given by the two models more and more significantly and the temperature and pressure peaks in the bubble given by the Gilmore-NASG model increase more significantly. With the rise of driving frequency, the difference between the results given by the two models gradually decreases and tends to be consistent under the high-frequency excitation. This indicates that the temperature and pressure in the bubble may arrive at higher values considering the compressibility of the medium caused by the co-volume changes of gas and surrounding liquid at different temperatures and pressures. In the meantime, the Gilmore-NASG model can accurately predict the changes in density, pressure and temperature of the liquid at the bubble wall as well as sound velocity, so this model has advantages in the study of bubble cavitation characteristics under high pressure and the effect of surrounding liquid on bubble cavitation characteristics. There will be important applications for the research on specific issues such as high-intensity focused ultrasound, shock wave lithotripsy treatment and sonochemistry.
-
Keywords:
- model /
- compressibility /
- cavitation characteristics /
- equation of state
[1] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[2] Gilmore F R 1952 California Institute of Technology Technical Report No. 26-4
[3] Brennen C E 1995 Cavitation and Bubble Dynamics (New York: Oxford University Press) p61
[4] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第236 −241页
Chen W Z 2014 Sound Cavitation Physics (Beijing: Science Press) pp236−241 (in Chinese)
[5] Prosperetti A, Lezzi A 1986 J. Fluid Mech. 168 457
Google Scholar
[6] Brenner M P, Hilgenfeldt S, Lohse D 2002 Rev. Mod. Phys. 74 425
Google Scholar
[7] Fuster D, Dopazo C, Hauke G 2011 J. Acoust. Soc. Am. 129 122
Google Scholar
[8] Merouani S, Hamdaoui O, Rezgui Y, Guemini M 2014 Ultrason. 54 227
Google Scholar
[9] Rosa M, Husseini G A, Pitt W G 2013 Ultrason. 53 97
Google Scholar
[10] Zilonova E, Solovchuk M, Sheu T 2018 Ultrason. Sonochem. 40 900
[11] Holzfuss J 2010 Proc. R. Soc. A 466 1829
Google Scholar
[12] Zhu S, Zhong P 1999 J. Acoust. Soc. Am. 106 3024
Google Scholar
[13] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[14] 清河美, 那仁满都拉 2019 68 234302
Google Scholar
Qinghim, Naranmandula 2019 Acta Phys. Sin. 68 234302
Google Scholar
[15] Nazari-Mahroo H, Pasandideh K, Navid H A, Sadighi-Bonabi R 2018 Phys. Lett. A 382 1962
Google Scholar
[16] Yuan L, Cheng H Y, Chu M C, Leung P T 1998 Phys. Rev. E 57 4265
Google Scholar
[17] Chandran J, Salih A 2019 Fluid Phase Equilib. 483 182
[18] Radulescu M I 2019 Phys. Fluids 31 111702
Google Scholar
[19] Radulescu M I 2020 Phys. Fluids 32 056101
Google Scholar
[20] Metayer O L, Saurel R 2016 Phys. Fluids 28 046102
Google Scholar
[21] Denner F 2021 Ultrason. Sonochem. 70 105307
[22] 杨德森, 江薇, 时胜国, 时洁, 张昊阳, 靳仕源 2013 哈尔滨工程大学学报 34 734
Yang D S, Jiang W, Shi S G, Shi J, Zhang H Y, Jin S Y 2013 Journal of Harbin Engineering University 34 734
[23] Kerboua K, Hamdaoui O 2018 Ultrason. Sonochem. 40 194
Google Scholar
[24] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[25] Moshaii A, Sadighi-Bonabi R, Taeibi-Rahni M 2004 J. Phys. Condens. Matter 16 1687
Google Scholar
[26] Nazari-Mahroo H, Pasandideh K, Navid H A, Sadighi-Bonabi R 2019 Ultrason. 102 106034
[27] Longwell P A, Olin J B, Sage B H 1958 Ind. Eng. Chem. Chem. Eng. Data Series 3 175
Google Scholar
[28] Hirschfelder J A, Curtiss C F, Bird R B 1954 Molecular theory of gases and liquids (New York: Wiley) pp293–302
[29] 姚允斌, 解涛, 高英敏 1985 物理化学手册 (上海: 科学技术出版社) 第119 页
Yao Y B, Xie T, Gao Y M 1985 Handbook of Physical Chemistry (Shanghai: Science and Technology Press) p119 (in Chinese)
[30] An Y 2006 Phys. Rev. E 74 026304
Google Scholar
[31] 姜李安, 陈伟中, 李晟琼, 卢美军, 王文杰 2003 声学技术 22 30
Google Scholar
Jiang L A, Chen W Z, Li S J, Lu M J, Wang W J 2003 Acoustic Technique 22 30
Google Scholar
[32] 郭策, 祝锡晶, 王建青, 叶林征 2016 65 044304
Google Scholar
Guo C, Zhu X J, Wang J Q, Ye L Z 2016 Acta Phys. Sin. 65 044304
Google Scholar
-
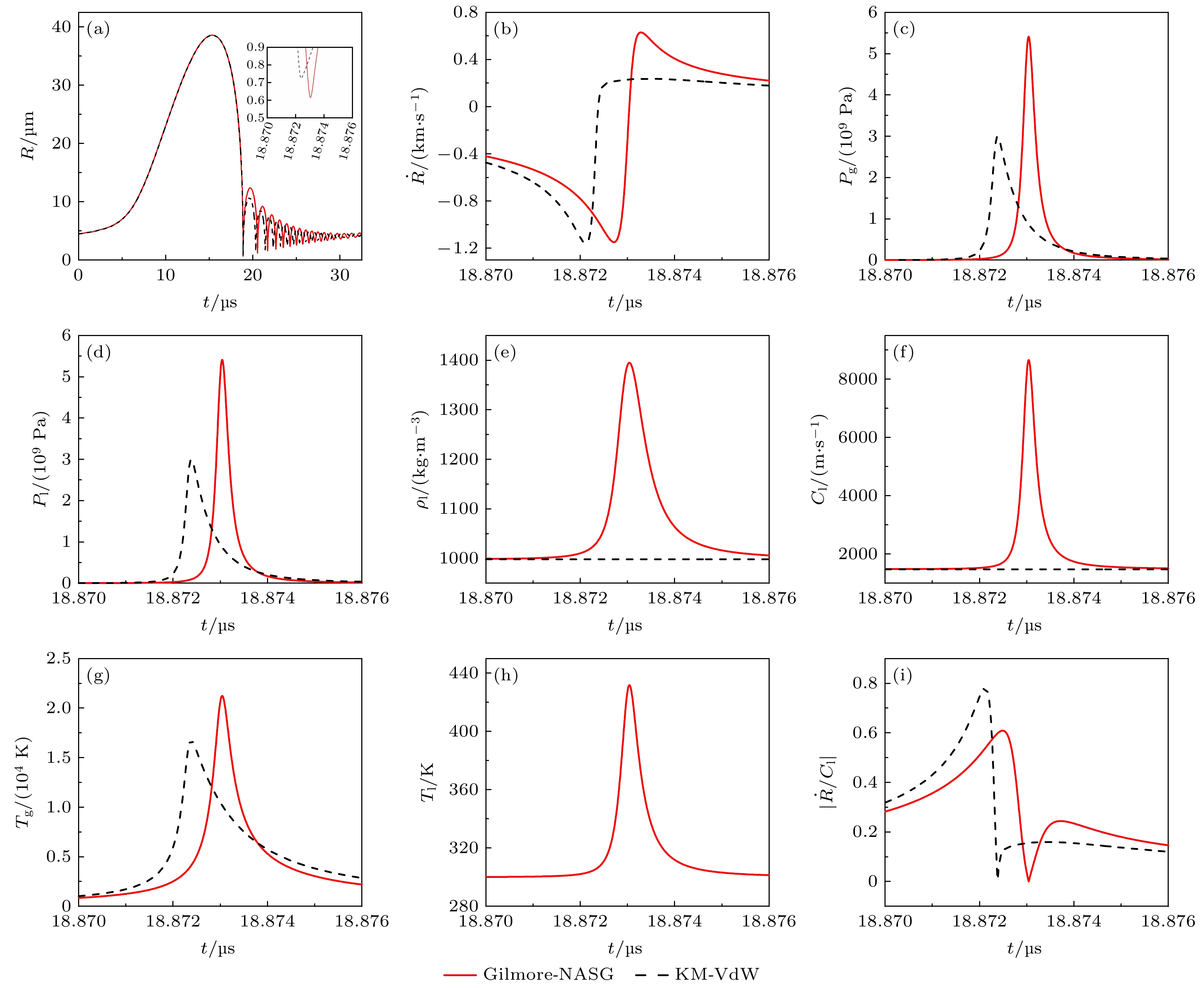
图 1 (a) 气泡半径变化; (b) 气泡壁速度变化; (c) 气泡内压力变化; (d) 气泡壁处液体压力变化; (e) 气泡壁处液体密度变化; (f) 气泡壁处液体中声速变化; (g) 气泡内温度变化; (h) 气泡壁处液体温度变化; (i) 气泡壁处液体马赫数变化
Fig. 1. (a) Change of bubble radius; (b) change of bubble wall velocity; (c) change of pressure in the bubble; (d) change of liquid pressure at the bubble wall; (e) change of liquid density at the bubble wall; (f) change of sound velocity in the liquid at the bubble wall; (g) change of temperature in the bubble; (h) change of liquid temperature at the bubble wall; (i) change of liquid Mach number at the bubble wall;
图 2 (a) 气泡最大半径、 (b) 最小半径 、(c) 崩溃速度和回弹速度、 (d) 液体最大马赫数、 (e) 泡内最大压力以及(f) 泡内最高温度, 随驱动声压幅值的变化
Fig. 2. (a) Maximum bubble radius, (b) minimum radius, (c) collapse speed and rebound speed, (d) maximum liquid Mach number, (e) maximum pressure in the bubble, and (f) maximum temperature in the bubble change with amplitude of driving sound pressure
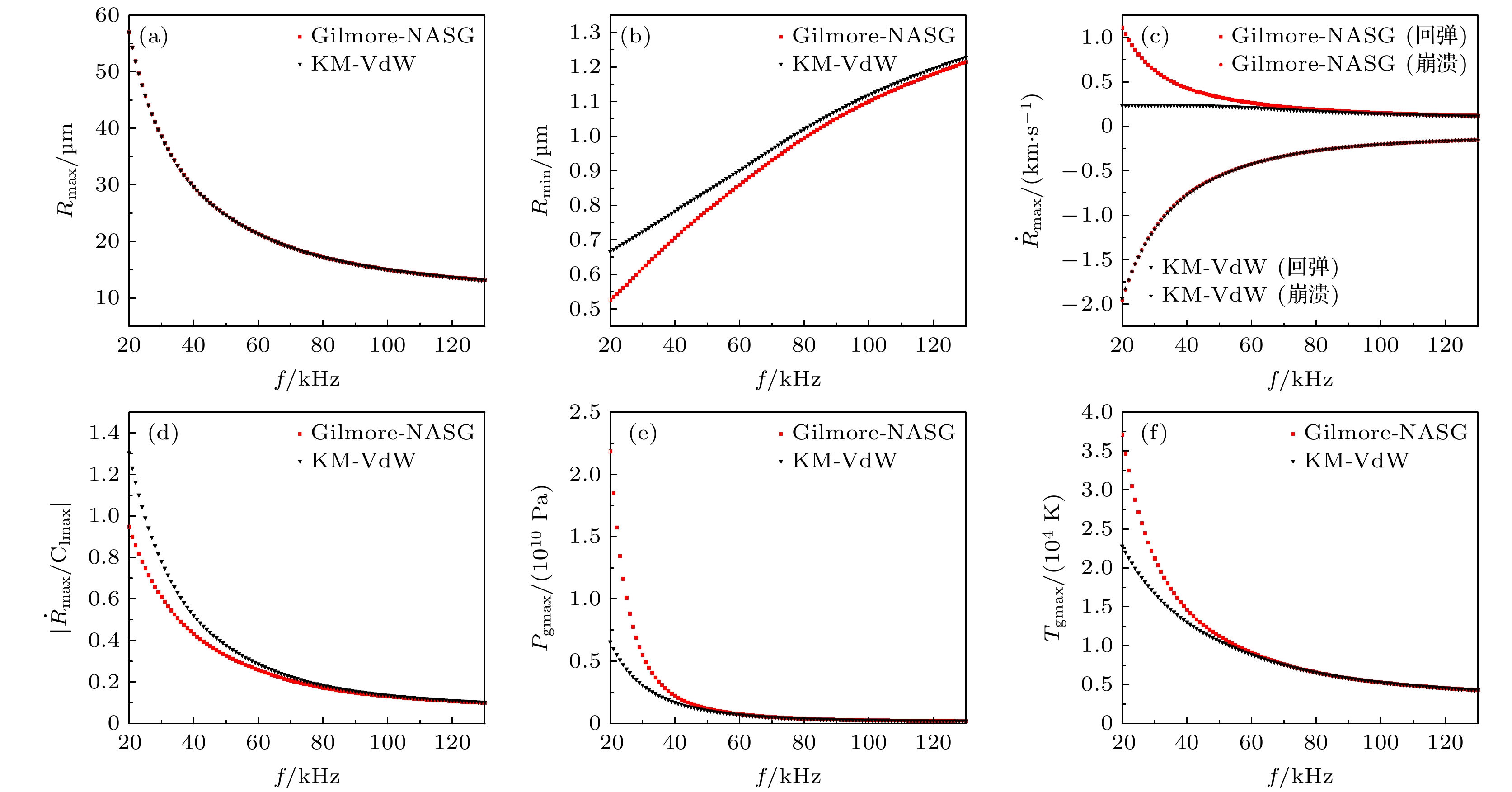
图 3 (a) 气泡最大半径、 (b) 最小半径、 (c) 崩溃速度和回弹速度、 (d) 液体最大马赫数 、(e) 泡内最大压力 以及(f) 泡内最高温度随驱动频率的变化
Fig. 3. (a) Maximum bubble radius, (b) minimum radius, (c) collapse speed and rebound speed, (d) maximum liquid Mach number, (e) maximum pressure in the bubble, and (f) maximum temperature in the bubble change with driving frequency
表 1 Gilmore-NASG模型中水和氩气的相关物理参数
Table 1. Physical parameters of water and argon in Gilmore-NASG model
参数 值 单位 环境密度$\rho_{\rm{l0}}$ 998 ${\rm{kg} }{\cdot} {\rm{m} }^{-3}$ $\rho_{\rm{g0}}$ 1.784 ${\rm{kg} }{\cdot}{\rm{m} }^{-3}$ 环境压力$P_{\rm{l0}}$ 101325 Pa $P_{\rm{g0}}$ 101325 Pa 表面张力σ 0.070 ${\rm{N} }{\cdot} {\rm{m} }^{-1}$ 切变黏滞系数η 0.001 ${\rm{Pa} }{\cdot} {\rm{s} }$ 体积黏滞系数λ 0.0041 ${\rm{Pa} }{\cdot} {\rm{s} }$ 环境声速$C_{\rm{l}}$ 1483 ${\rm{m} } {\cdot} {\rm{s} }^{-1}$ 环境温度$T_{\rm{l0}}$ 300 K $T_{\rm{g0}}$ 300 K 分子共体积$b_{\rm{l}}$ $6.6766\times 10^{-4}$ ${\rm{m} }^3{\cdot} {\rm{kg} }^{-1}$ $b_{\rm{g}}$ $4.778\times 10^{-4}$ ${\rm{m} }^3{\cdot}{\rm{kg} }^{-1}$ 压力常数$B_{\rm{l}}$ $6.1534\times 10^8$ Pa $B_{\rm{g}}$ 0 Pa 多方指数$\varGamma_{\rm{l} }$ 1.19 — $\varGamma_{\rm{g} }$ 1.67 — 注: 水的体积黏滞系数λ的取值参考了文献[25]. 
下载: 导出CSV
表 2 KM-VdW模型中水和氩气的相关物理参数
Table 2. Physical parameters of water and argon in KM-VdW model
参数 值 单位 环境密度$ \rho_{{\rm{l}}} $ 998 ${\rm{kg} }{\cdot} {\rm{m} }^{-3}$ 环境压力$ P_{\rm{g0}} $ 101325 Pa 表面张力σ 0.070 ${\rm{N} }{\cdot}{\rm{m} }^{-1}$ 切变黏滞系数η 0.001 ${\rm{Pa} }{\cdot} {\rm{s} }$ 体积黏滞系数λ 0.0041 ${\rm{Pa} }{\cdot} {\rm{s} }$ 环境声速$ C_{\rm{l}} $ 1483 ${\rm{m} }{\cdot} {\rm{s} }^{-1}$ 环境温度$ T_{\rm{g0}} $ 300 K 范德瓦耳斯常数a 0.1345 ${\rm{Pa} }{\cdot} {\rm{m} }^{6}{\cdot} {\rm{mol} }^{-2}$ b $ 3.219\times 10^{-5} $ ${\rm{m} }^{3}{\cdot} {\rm{mol} }^{-1}$ 摩尔数m $ 2.02339\times 10^{-14} $ — 多方指数$\varGamma_{\rm{g} }$ 1.67 —
下载: 导出CSV
-
[1] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[2] Gilmore F R 1952 California Institute of Technology Technical Report No. 26-4
[3] Brennen C E 1995 Cavitation and Bubble Dynamics (New York: Oxford University Press) p61
[4] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第236 −241页
Chen W Z 2014 Sound Cavitation Physics (Beijing: Science Press) pp236−241 (in Chinese)
[5] Prosperetti A, Lezzi A 1986 J. Fluid Mech. 168 457
Google Scholar
[6] Brenner M P, Hilgenfeldt S, Lohse D 2002 Rev. Mod. Phys. 74 425
Google Scholar
[7] Fuster D, Dopazo C, Hauke G 2011 J. Acoust. Soc. Am. 129 122
Google Scholar
[8] Merouani S, Hamdaoui O, Rezgui Y, Guemini M 2014 Ultrason. 54 227
Google Scholar
[9] Rosa M, Husseini G A, Pitt W G 2013 Ultrason. 53 97
Google Scholar
[10] Zilonova E, Solovchuk M, Sheu T 2018 Ultrason. Sonochem. 40 900
[11] Holzfuss J 2010 Proc. R. Soc. A 466 1829
Google Scholar
[12] Zhu S, Zhong P 1999 J. Acoust. Soc. Am. 106 3024
Google Scholar
[13] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[14] 清河美, 那仁满都拉 2019 68 234302
Google Scholar
Qinghim, Naranmandula 2019 Acta Phys. Sin. 68 234302
Google Scholar
[15] Nazari-Mahroo H, Pasandideh K, Navid H A, Sadighi-Bonabi R 2018 Phys. Lett. A 382 1962
Google Scholar
[16] Yuan L, Cheng H Y, Chu M C, Leung P T 1998 Phys. Rev. E 57 4265
Google Scholar
[17] Chandran J, Salih A 2019 Fluid Phase Equilib. 483 182
[18] Radulescu M I 2019 Phys. Fluids 31 111702
Google Scholar
[19] Radulescu M I 2020 Phys. Fluids 32 056101
Google Scholar
[20] Metayer O L, Saurel R 2016 Phys. Fluids 28 046102
Google Scholar
[21] Denner F 2021 Ultrason. Sonochem. 70 105307
[22] 杨德森, 江薇, 时胜国, 时洁, 张昊阳, 靳仕源 2013 哈尔滨工程大学学报 34 734
Yang D S, Jiang W, Shi S G, Shi J, Zhang H Y, Jin S Y 2013 Journal of Harbin Engineering University 34 734
[23] Kerboua K, Hamdaoui O 2018 Ultrason. Sonochem. 40 194
Google Scholar
[24] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[25] Moshaii A, Sadighi-Bonabi R, Taeibi-Rahni M 2004 J. Phys. Condens. Matter 16 1687
Google Scholar
[26] Nazari-Mahroo H, Pasandideh K, Navid H A, Sadighi-Bonabi R 2019 Ultrason. 102 106034
[27] Longwell P A, Olin J B, Sage B H 1958 Ind. Eng. Chem. Chem. Eng. Data Series 3 175
Google Scholar
[28] Hirschfelder J A, Curtiss C F, Bird R B 1954 Molecular theory of gases and liquids (New York: Wiley) pp293–302
[29] 姚允斌, 解涛, 高英敏 1985 物理化学手册 (上海: 科学技术出版社) 第119 页
Yao Y B, Xie T, Gao Y M 1985 Handbook of Physical Chemistry (Shanghai: Science and Technology Press) p119 (in Chinese)
[30] An Y 2006 Phys. Rev. E 74 026304
Google Scholar
[31] 姜李安, 陈伟中, 李晟琼, 卢美军, 王文杰 2003 声学技术 22 30
Google Scholar
Jiang L A, Chen W Z, Li S J, Lu M J, Wang W J 2003 Acoustic Technique 22 30
Google Scholar
[32] 郭策, 祝锡晶, 王建青, 叶林征 2016 65 044304
Google Scholar
Guo C, Zhu X J, Wang J Q, Ye L Z 2016 Acta Phys. Sin. 65 044304
Google Scholar
下载:
计量
- 文章访问数: 4975
- PDF下载量: 108
- 被引次数: 0
