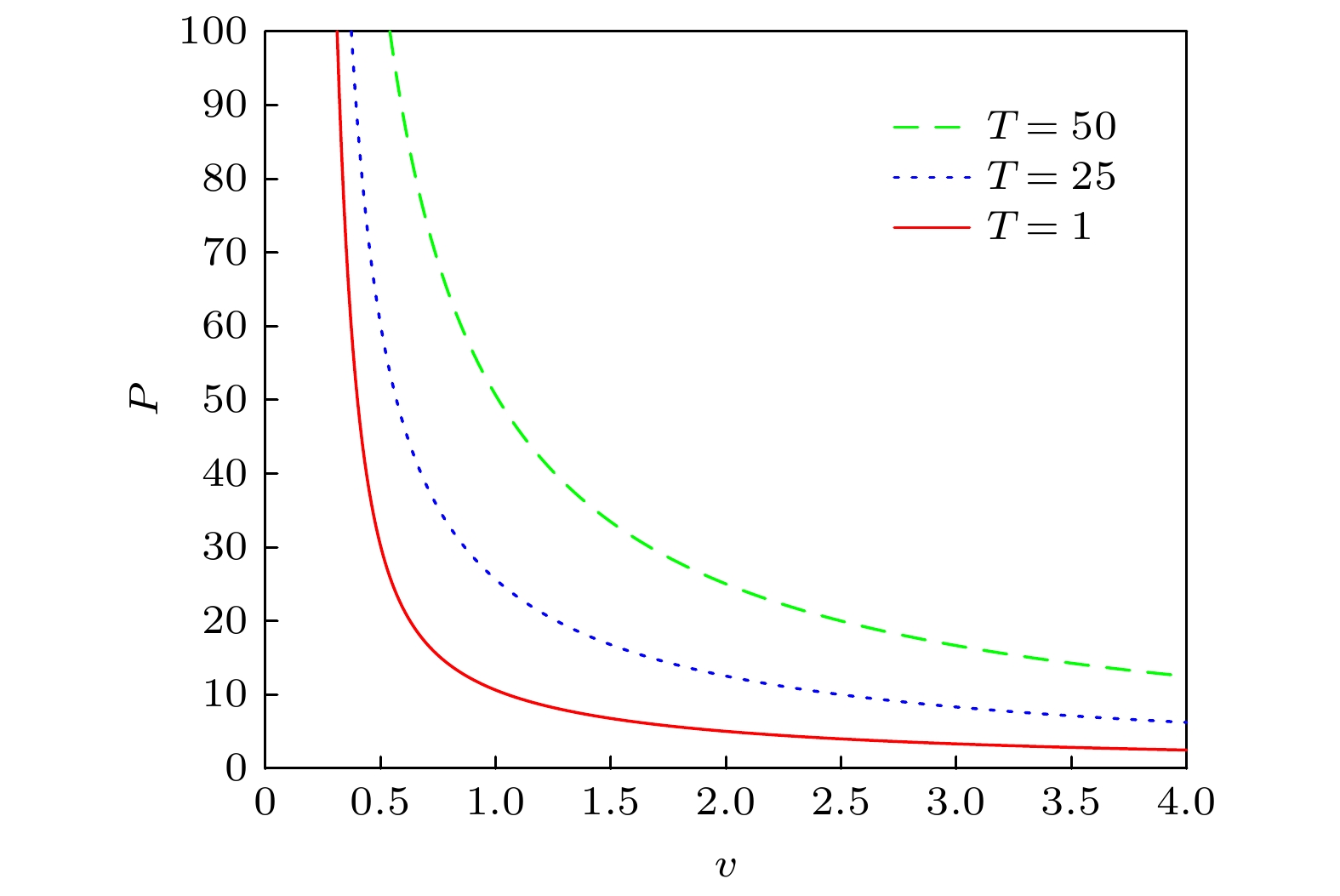
-
The thermodynamic functions of toroidal black holes are investigated in this paper by taking the cosmological constant as a dynamic variable equivalent to the pressure. The equation of state and the Smarr relation of a toroidal black hole are given. Then, the Gibbs function is obtained by calculating the Euclidian action. Further we study other thermodynamic functions of the toroidal black hole, such as free energy, internal energy, and thermodynamic enthalpy. The heat capacity of the toroidal black hole at constant pressure and constant volume is obtained. The results show that toroidal black holes have no van der Waals type phase transition. Toroidal black hole is a stable thermodynamic system because its heat capacity at constant pressure is greater than zero and its heat capacity at constant volume is equal to zero.
[1] Bekenstein J D 1973 Phys. Rev. D 7 2333
Google Scholar
[2] Bekenstein J D 1974 Phys. Rev. D 9 3292
Google Scholar
[3] Hawking S W 1975 Commun. Math. Phys. 43 199
Google Scholar
[4] Caldarelli M M, Cognola G, Klemm D 2000 Class. Quantum Grav. 17 399
Google Scholar
[5] Kastor D, Ray S, Traschen J 2009 Class. Quantum Grav. 26 195011
Google Scholar
[6] Dolan B P 2011 Class. Quantum Grav. 28 125020
Google Scholar
[7] Dolan B P 2011 Class. Quantum Grav. 28 235017
Google Scholar
[8] Dolan B P 2011 Phys. Rev. D 84 127503
Google Scholar
[9] Cvetic M, Gibbons G W, Kubizňák D, Pope C N 2011 Phys. Rev. D 84 024037
Google Scholar
[10] Lu H, Pang Y, Pope C N, et al. 2012 Phys. Rev. D 86 044011
Google Scholar
[11] Gibbons G W, Hawking S W 1977 Phys. Rev. D 15 2752
Google Scholar
[12] Kubizňák D, Mann R B 2012 JHEP 7 1
Google Scholar
[13] Wang B B 2004 Gen. Relat. Gravit. 36 735
Google Scholar
[14] Wang B B 2008 Chin. Phys. B 17 467
Google Scholar
[15] Goenner H, Stachel J 1970 J. Math. Phys. 11 3358
Google Scholar
[16] Huang C G, Liang C B 1995 Phys. Lett. A 201 27
Google Scholar
[17] 梁灿彬, 周彬 2009 微分几何入门与广义相对论(下册) 第二版 (北京: 科学出版社) 第116页
Liang C B, Zhou B 2009 Introduction to Differential Geometry and General Relativity (Vol. 2) (2nd Ed.) (Beijing: Science Press) p116 (in Chinese)
[18] Gauntlett J P, Myers R C, Townsend P K 1999 Class. Quant. Grav. 16 1
Google Scholar
[19] Townsend P. K. and Zamaklar M. 2001 Class. Quant. Grav. 18 5269
Google Scholar
-
[1] Bekenstein J D 1973 Phys. Rev. D 7 2333
Google Scholar
[2] Bekenstein J D 1974 Phys. Rev. D 9 3292
Google Scholar
[3] Hawking S W 1975 Commun. Math. Phys. 43 199
Google Scholar
[4] Caldarelli M M, Cognola G, Klemm D 2000 Class. Quantum Grav. 17 399
Google Scholar
[5] Kastor D, Ray S, Traschen J 2009 Class. Quantum Grav. 26 195011
Google Scholar
[6] Dolan B P 2011 Class. Quantum Grav. 28 125020
Google Scholar
[7] Dolan B P 2011 Class. Quantum Grav. 28 235017
Google Scholar
[8] Dolan B P 2011 Phys. Rev. D 84 127503
Google Scholar
[9] Cvetic M, Gibbons G W, Kubizňák D, Pope C N 2011 Phys. Rev. D 84 024037
Google Scholar
[10] Lu H, Pang Y, Pope C N, et al. 2012 Phys. Rev. D 86 044011
Google Scholar
[11] Gibbons G W, Hawking S W 1977 Phys. Rev. D 15 2752
Google Scholar
[12] Kubizňák D, Mann R B 2012 JHEP 7 1
Google Scholar
[13] Wang B B 2004 Gen. Relat. Gravit. 36 735
Google Scholar
[14] Wang B B 2008 Chin. Phys. B 17 467
Google Scholar
[15] Goenner H, Stachel J 1970 J. Math. Phys. 11 3358
Google Scholar
[16] Huang C G, Liang C B 1995 Phys. Lett. A 201 27
Google Scholar
[17] 梁灿彬, 周彬 2009 微分几何入门与广义相对论(下册) 第二版 (北京: 科学出版社) 第116页
Liang C B, Zhou B 2009 Introduction to Differential Geometry and General Relativity (Vol. 2) (2nd Ed.) (Beijing: Science Press) p116 (in Chinese)
[18] Gauntlett J P, Myers R C, Townsend P K 1999 Class. Quant. Grav. 16 1
Google Scholar
[19] Townsend P. K. and Zamaklar M. 2001 Class. Quant. Grav. 18 5269
Google Scholar
下载:
计量
- 文章访问数: 3513
- PDF下载量: 75
- 被引次数: 0
