-
研究复杂海洋环境中海底地震波激发及其传播特性, 对海底物理力学特性研究、资源勘探等具有重要的意义. 目前针对时域海底地震波的研究大都局限于水平分层的情况, 而实际的海底地质条件比较复杂, 基于理想环境假设得出的数值解与实际差别较大. 本文在考虑倾斜、隆起等非水平海底模型的情形下, 采用时间2阶精度、空间10阶精度的交错网格有限差分方法, 同时结合多轴完全匹配层边界条件, 对复杂海洋环境下的海底地震波进行时域数值模拟与分析. 利用计算得到的声场时域波形, 分析了复杂海洋环境下海底地震波的传播特性. 结果表明, 采用空间高阶精度的交错网格有限差分方法, 可改善数值计算中的频散问题; 同时采用多轴完全匹配层替代传统的完全匹配层, 解决了液-固介质中远距离声场数值模拟不稳定的问题. 在含倾斜与隆起构造的复杂海底模型中, 海底基岩隆起改变了Scholte波的传播方向, 更有利于在较浅深度处接收到Scholte波.
-
关键词:
- 海底地震波 /
- 复杂海底 /
- 高阶交错网格时域有限差分 /
- 多轴完全匹配层
The studying of the excitation and propagation characteristics of seabed seismic waves in a complex marine environment is of great significance in investigating seafloor physical and mechanical properties and exploring resources. At present, the research of time-domain seabed seismic waves is mostly restricted in a marine environment with horizontal stratification, but the actual geological conditions of seafloor are relatively complex, and the numerical solutions obtained under ideal assumption are quite different from those in an actual complex environment. To master the propagation characteristics of seabed seismic wave in the environment that is closer to the actual one, a complex and long range model including layers of water, soft mud and bedrocks is designed in the paper, where non-horizontal seafloor topography with a dipping and uplifting structure is considered. The staggered-grid finite difference method with 2nd-order accuracy in time and 10th-order accuracy in space is used to simulate the seabed seismic waves under such a complex marine environment. Meanwhile, multi axial perfectly matched layer is used as an artificial boundary condition to ensure the numerical long-term stability in a liquid-solid medium. Considering the dipping structure, the acoustic signals excited by sources at different positions of the model are compared to determine the favorable style of source excitation for Scholte interface wave receiving. Through the time-domain waveform of the calculated acoustic field, the propagation characteristics of the seabed seismic wave in the complex marine environment are analyzed. The results show that the staggered-grid finite difference method with high-order spatial accuracy can improve the dispersion problem in numerical calculation. The multi-axial perfectly matched layer used to replace the traditional perfectly matched layer can solve the instability problem in the numerical simulation of acoustic field in liquid-solid media for a long range. Through the comparison among the acoustic signal amplitudes excited by sources at different positions, a better performance can be achieved when the source-receiver is placed along the updip direction. In such a case, the acoustic signal is stronger, which is more advantageous to receive and analyze the Scholte interface wave. In the complex seabed model with a dipping and uplifting structure, the uplift of seafloor bedrock changes the propagation direction of Scholte wave, which makes it possible to receive Scholte wave at shallower depth.-
Keywords:
- seabed seismic wave /
- complex seafloor topography /
- time domain high-order staggered-grid finite difference /
- multi-axial perfectly matched layer
[1] 胡治国, 李整林, 张仁和, 任云, 秦继兴, 何利 2016 65 221
Google Scholar
Hu Z G, Li Z L, Zhang R H, Ren Y, Qin J X, He L 2016 Acta Phys. Sin. 65 221
Google Scholar
[2] 胡常青, 朱玮, 何远清, 文龙贻彬, 杨义勇 2019 导航与控制 18 1
Google Scholar
Hu C Q, Zhu W, He Y Q, WenLong Y B, Yang Y Y 2019 Navi. Ctrl. 18 1
Google Scholar
[3] 仇浩淼, 夏唐代, 何绍衡, 陈炜昀 2018 67 204302
Google Scholar
Qiu H M, Xia T D, He S H, Chen W Y 2018 Acta Phys. Sin. 67 204302
Google Scholar
[4] Scholte J 1947 Geophys. J. Int. 5 120
Google Scholar
[5] 马琦, 胡文祥, 徐琰锋, 王浩 2017 66 084302
Google Scholar
Ma Q, Hu W X, Xu Y F, Wang H 2017 Acta Phys. Sin. 66 084302
Google Scholar
[6] 卢再华, 张志宏, 顾建农 2009 声学技术 28 596
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2009 Tech. Acoust. 28 596
Google Scholar
[7] 卢再华, 张志宏, 顾建农 2011 海军工程大学学报 23 63
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2011 J. Nav. Uni. Eng. 23 63
Google Scholar
[8] 韩庆邦, 徐杉, 谢祖峰, 葛蕤, 王茜, 赵胜永, 朱昌平 2013 62 194301
Google Scholar
Han Q B, Xu S, Xie Z F, Ge R, Wang X, Zhao S Y, Zhu C P 2013 Acta Phys. Sin. 62 194301
Google Scholar
[9] 左雷, 孟路稳, 金丹, 李静威 2017 海军工程大学学报 29 13
Google Scholar
Zuo L, Meng L W, Jin D, Li J W 2017 J. Nav. Uni. Eng. 29 13
Google Scholar
[10] 孟路稳, 程广利, 陈亚男, 张明敏 2017 兵工学报 38 319
Google Scholar
Meng L W, Cheng G L, Chen Y N, Zhang M M 2017 Acta Armam. 38 319
Google Scholar
[11] 卢再华, 张志宏, 顾建农 2007 应用力学学报 24 54
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2007 Chin. J. Appl. Mech. 24 54
Google Scholar
[12] 卢再华, 张志宏, 顾建农 2014 兵工学报 35 2065
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2014 Acta Armam. 35 2065
Google Scholar
[13] 任波, 吴强, 张自圃 2017 电子世界 17 19
Google Scholar
Ren B, Wu Q, Zhang Z P 2017 Electron. World 17 19
Google Scholar
[14] 李整林, 张仁和, 鄢锦, 彭朝晖, 李风华 2003 声学学报 28 425
Google Scholar
Li Z L, Zhang R H, Yan J, Peng Z H, Li F H 2003 Acta Acustica. 28 425
Google Scholar
[15] 祝捍皓, 郑红, 林建民, 汤云峰, 孔令明 2016 上海交通大学学报 50 257
Google Scholar
Zhu H H, Zheng H, Lin J M, Tang Y F, Kong L M 2016 J. Shanghai Jiaotong Univ. 50 257
Google Scholar
[16] 孟路稳, 程广利, 罗夏云, 张明敏 2018 哈尔滨工程大学学报 39 384
Google Scholar
Meng L W, Cheng G L, Luo X Y, Zhang M M 2018 J. Harbin Eng. Univ. 39 384
Google Scholar
[17] Dai N, Vafidis A, Kanasewich E R 1995 Geophys. 60 327
Google Scholar
[18] 董良国, 马在田, 曹景忠, 王华忠, 耿建华, 雷兵, 许世勇 2000 地球 43 411
Google Scholar
Dong L G, Ma Z T, Cao J Z, Wang H Z, Geng J H, Lei B, Xu S Y 2000 Chin. J. Geophys. 43 411
Google Scholar
[19] Meza-Fajardo K C, Papageorgiou A S 2008 B. Seismol. Soc. Am. 98 1811
Google Scholar
[20] Meza-Fajardo K C, Papageorgiou A S 2012 B. Seismol. Soc. Am. 102 2458
Google Scholar
[21] 王颖, 陈浩 2018 应用声学 37 849
Google Scholar
Wang Y, Chen H 2018 J. Appl. Acoust. 37 849
Google Scholar
[22] Bécache E, Fauqueux S, Joly P 2003 J. Comput. Phys. 188 399
Google Scholar
[23] Zeng C, Xia J H, Miller R D, Tsoflias G P 2012 Geophysics 77 T1
-
图 2 空间4阶精度的波形记录和时频分析结果 (a)时域波形; (b)时频分析
Fig. 2. Seismogram and frequency domain result by method with 4 th order spatial accuracy: (a) Time domain waveform; (b) Time-frequency analysis.
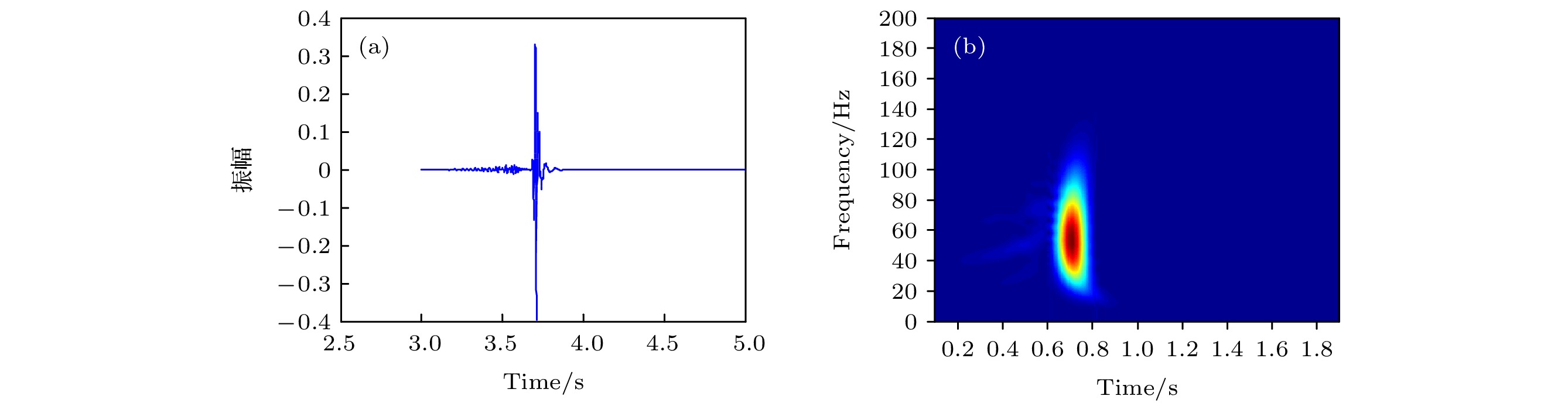
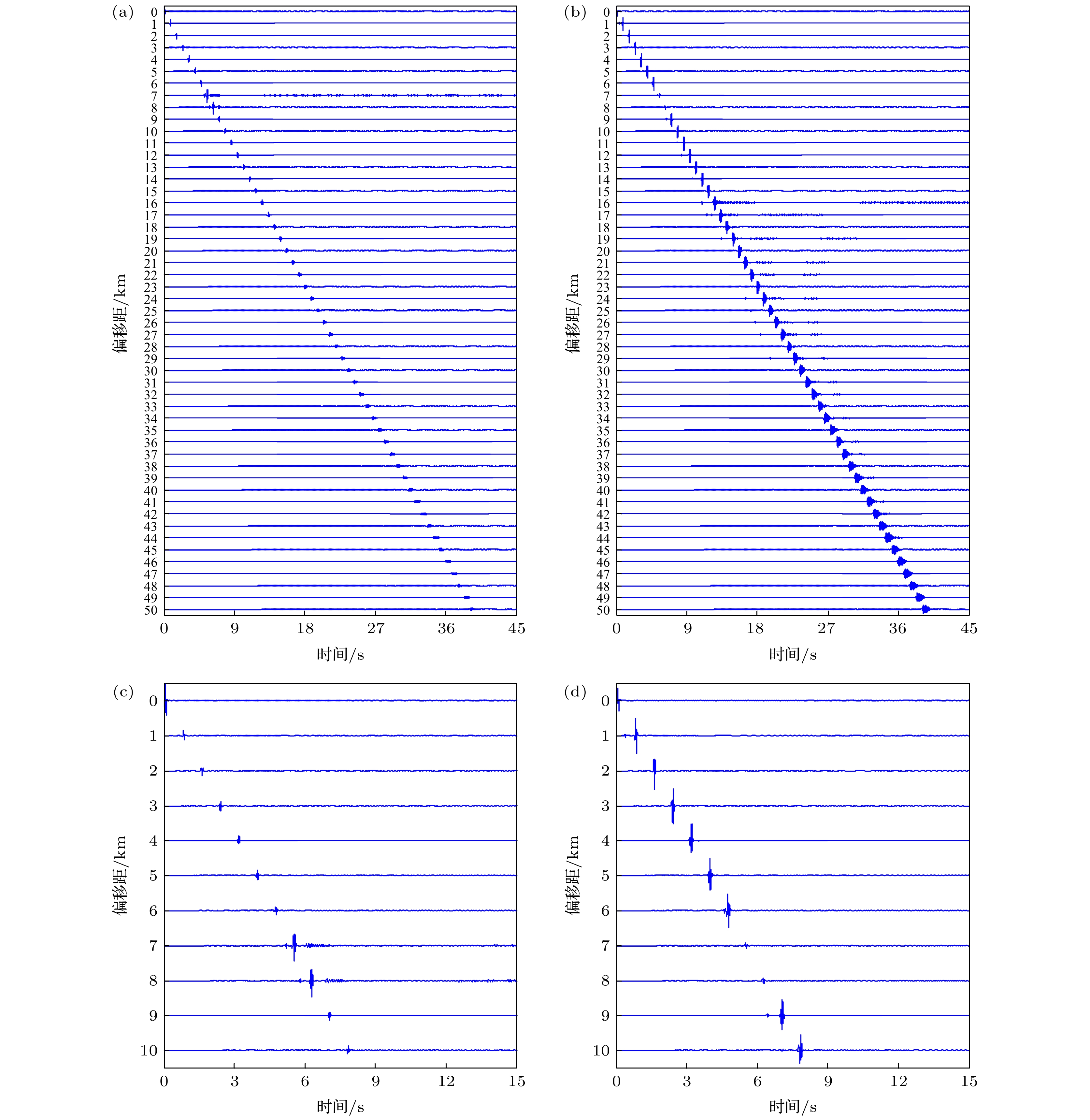
图 3 源距5 km深度为50 m的波形记录和频域结果 (a)时域波形, 时间步长为0.1 ms; (b)时频分析, 时间步长为0.1 ms; (c)时域波形, 时间步长为0.05 ms; (d)时频分析, 时间步长为0.05 ms
Fig. 3. Seismogram and frequency domain result of offset 5 km and depth 50 m: (a) Time domain waveform, time step is 0.1 ms; (b) Time-frequency analysis, time step is 0.1 ms; (c) Time Domain waveform, time step is 0.05 ms; (d) Time-frequency analysis, time step is 0.05 ms.
图 4 源距5 km深度为50 m的波形记录和频域结果, 空间网格大小为1 m (a)时域波形; (b)时频分析
Fig. 4. Seismogram and frequency domain result of offset 5 km and depth 50 m, with spatial interval 1 m: (a) Time domain waveform; (b) Time-frequency analysis.
图 5 空间10阶精度的波形记录和频域结果 (a)时域波形; (b)时频分析
Fig. 5. Seismogram and frequency domain result by method with 10 th order spatial accuracy: (a) Time domain waveform; (b) Time-frequency analysis.
图 7 复杂海底模型 (a) 模型及隆起构造放大显示; (b)海水层声速曲线
Fig. 7. Model with complex seafloor topography: (a) Whole model and zoomed display of uplift structure; (b) Sound speed profile of sea water.
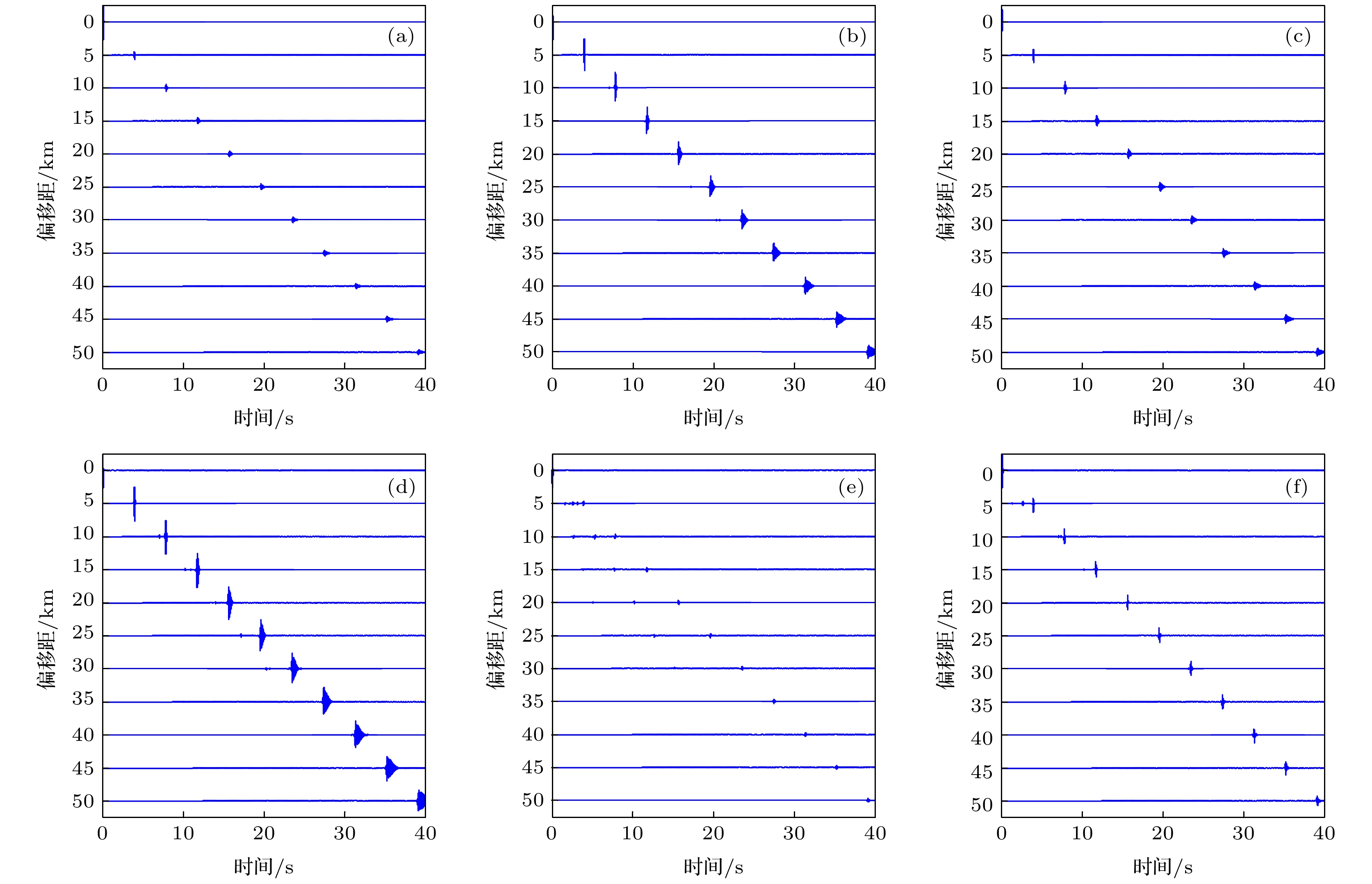
图 8 不同界面处的接收记录 (a) 界面1, 震源在左; (b) 界面1, 震源在右; (c) 界面2, 震源在左; (d) 界面2, 震源在右; (e) 界面3, 震源在左; (f) 界面3, 震源在右
Fig. 8. Records at different interfaces: (a) Interface 1, the source is on the left; (b) Interface 1, the source is on the right; (c) Interface 2, the source is on the left; (d) Interface 2, the source is on the right; (e) Interface 3, the source is on the left; (f) Interface 3, the source is on the right.
图 9 不同界面处的接收记录 (a) 界面1, 偏移距 ≤ 50 km; (b) 界面2, 偏移距 ≤ 50 km; (c) 界面1, 偏移距 ≤ 10 km; (d) 界面2, 偏移距 ≤ 10 km
Fig. 9. Records at different interfaces: (a) Interface 1, offset ≤ 50 km; (b) Interface 2, offset ≤ 50 km; (c) Interface 1, offset ≤ 10 km; (d) Interface 2, offset ≤ 10 km.
图 10 隆起处的波形记录 (a) 偏移距9 km; (b) 偏移距8 km; (c) 偏移距7 km; (d) 偏移距6 km
Fig. 10. Seismograms at uplit structure: (a) Offset 9 km; (b) Offset 8 km; (c) Offset 7 km; (d) Offset 6 km.
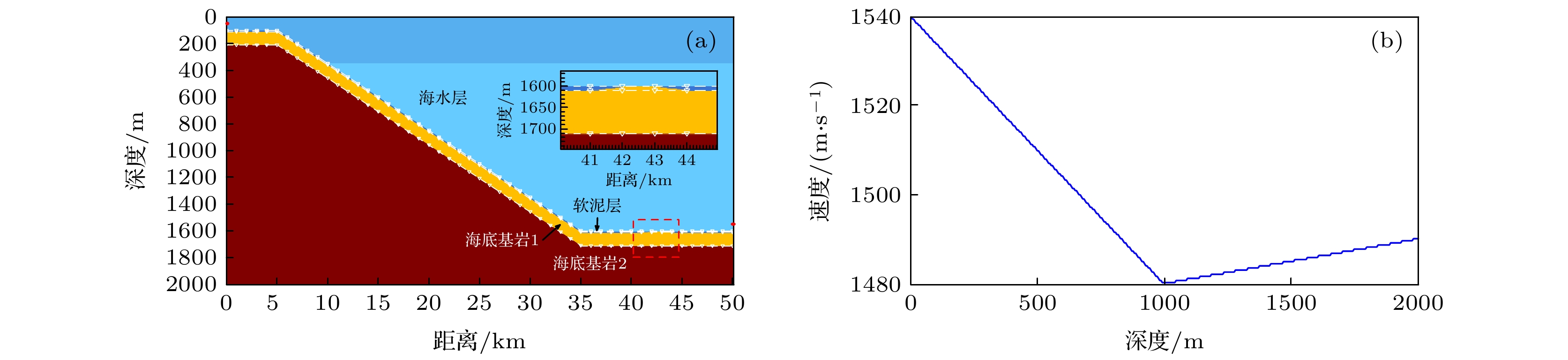
表 1 含倾斜与隆起的模型参数
Table 1. Parameters of model including slope and uplift
层 纵波速度
Vp/(${\text{m} }/{ {\text{s} }}$)横波速度
Vs/(${\text{m} }/{ {\text{s} }^{} }$)密度
ρ/(${\text{kg} }/{ {\text{m} }^{3} }$)厚度
d/m海水 1480—1540 0 1000 100—1600 软泥 1600 0 1750 0—10 海底
基岩13200 1800 1850 100—110 海底
基岩24000 2000 2000 ∞ 
下载: 导出CSV
-
[1] 胡治国, 李整林, 张仁和, 任云, 秦继兴, 何利 2016 65 221
Google Scholar
Hu Z G, Li Z L, Zhang R H, Ren Y, Qin J X, He L 2016 Acta Phys. Sin. 65 221
Google Scholar
[2] 胡常青, 朱玮, 何远清, 文龙贻彬, 杨义勇 2019 导航与控制 18 1
Google Scholar
Hu C Q, Zhu W, He Y Q, WenLong Y B, Yang Y Y 2019 Navi. Ctrl. 18 1
Google Scholar
[3] 仇浩淼, 夏唐代, 何绍衡, 陈炜昀 2018 67 204302
Google Scholar
Qiu H M, Xia T D, He S H, Chen W Y 2018 Acta Phys. Sin. 67 204302
Google Scholar
[4] Scholte J 1947 Geophys. J. Int. 5 120
Google Scholar
[5] 马琦, 胡文祥, 徐琰锋, 王浩 2017 66 084302
Google Scholar
Ma Q, Hu W X, Xu Y F, Wang H 2017 Acta Phys. Sin. 66 084302
Google Scholar
[6] 卢再华, 张志宏, 顾建农 2009 声学技术 28 596
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2009 Tech. Acoust. 28 596
Google Scholar
[7] 卢再华, 张志宏, 顾建农 2011 海军工程大学学报 23 63
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2011 J. Nav. Uni. Eng. 23 63
Google Scholar
[8] 韩庆邦, 徐杉, 谢祖峰, 葛蕤, 王茜, 赵胜永, 朱昌平 2013 62 194301
Google Scholar
Han Q B, Xu S, Xie Z F, Ge R, Wang X, Zhao S Y, Zhu C P 2013 Acta Phys. Sin. 62 194301
Google Scholar
[9] 左雷, 孟路稳, 金丹, 李静威 2017 海军工程大学学报 29 13
Google Scholar
Zuo L, Meng L W, Jin D, Li J W 2017 J. Nav. Uni. Eng. 29 13
Google Scholar
[10] 孟路稳, 程广利, 陈亚男, 张明敏 2017 兵工学报 38 319
Google Scholar
Meng L W, Cheng G L, Chen Y N, Zhang M M 2017 Acta Armam. 38 319
Google Scholar
[11] 卢再华, 张志宏, 顾建农 2007 应用力学学报 24 54
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2007 Chin. J. Appl. Mech. 24 54
Google Scholar
[12] 卢再华, 张志宏, 顾建农 2014 兵工学报 35 2065
Google Scholar
Lu Z H, Zhang Z H, Gu J N 2014 Acta Armam. 35 2065
Google Scholar
[13] 任波, 吴强, 张自圃 2017 电子世界 17 19
Google Scholar
Ren B, Wu Q, Zhang Z P 2017 Electron. World 17 19
Google Scholar
[14] 李整林, 张仁和, 鄢锦, 彭朝晖, 李风华 2003 声学学报 28 425
Google Scholar
Li Z L, Zhang R H, Yan J, Peng Z H, Li F H 2003 Acta Acustica. 28 425
Google Scholar
[15] 祝捍皓, 郑红, 林建民, 汤云峰, 孔令明 2016 上海交通大学学报 50 257
Google Scholar
Zhu H H, Zheng H, Lin J M, Tang Y F, Kong L M 2016 J. Shanghai Jiaotong Univ. 50 257
Google Scholar
[16] 孟路稳, 程广利, 罗夏云, 张明敏 2018 哈尔滨工程大学学报 39 384
Google Scholar
Meng L W, Cheng G L, Luo X Y, Zhang M M 2018 J. Harbin Eng. Univ. 39 384
Google Scholar
[17] Dai N, Vafidis A, Kanasewich E R 1995 Geophys. 60 327
Google Scholar
[18] 董良国, 马在田, 曹景忠, 王华忠, 耿建华, 雷兵, 许世勇 2000 地球 43 411
Google Scholar
Dong L G, Ma Z T, Cao J Z, Wang H Z, Geng J H, Lei B, Xu S Y 2000 Chin. J. Geophys. 43 411
Google Scholar
[19] Meza-Fajardo K C, Papageorgiou A S 2008 B. Seismol. Soc. Am. 98 1811
Google Scholar
[20] Meza-Fajardo K C, Papageorgiou A S 2012 B. Seismol. Soc. Am. 102 2458
Google Scholar
[21] 王颖, 陈浩 2018 应用声学 37 849
Google Scholar
Wang Y, Chen H 2018 J. Appl. Acoust. 37 849
Google Scholar
[22] Bécache E, Fauqueux S, Joly P 2003 J. Comput. Phys. 188 399
Google Scholar
[23] Zeng C, Xia J H, Miller R D, Tsoflias G P 2012 Geophysics 77 T1
下载:
计量
- 文章访问数: 4207
- PDF下载量: 79
- 被引次数: 0
