基于Marangoni效应的液-液驱动铺展过程

赵文景; 王进; 秦威广; 纪文杰; 蓝鼎; 王育人

doi:10.7498/aps.70.20210485

摘要

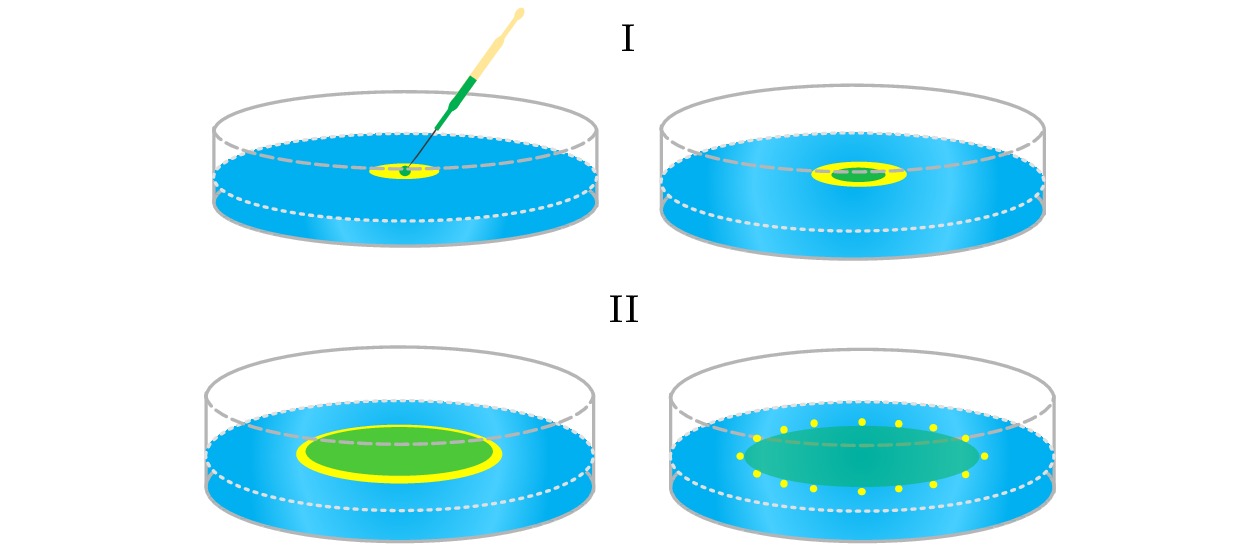
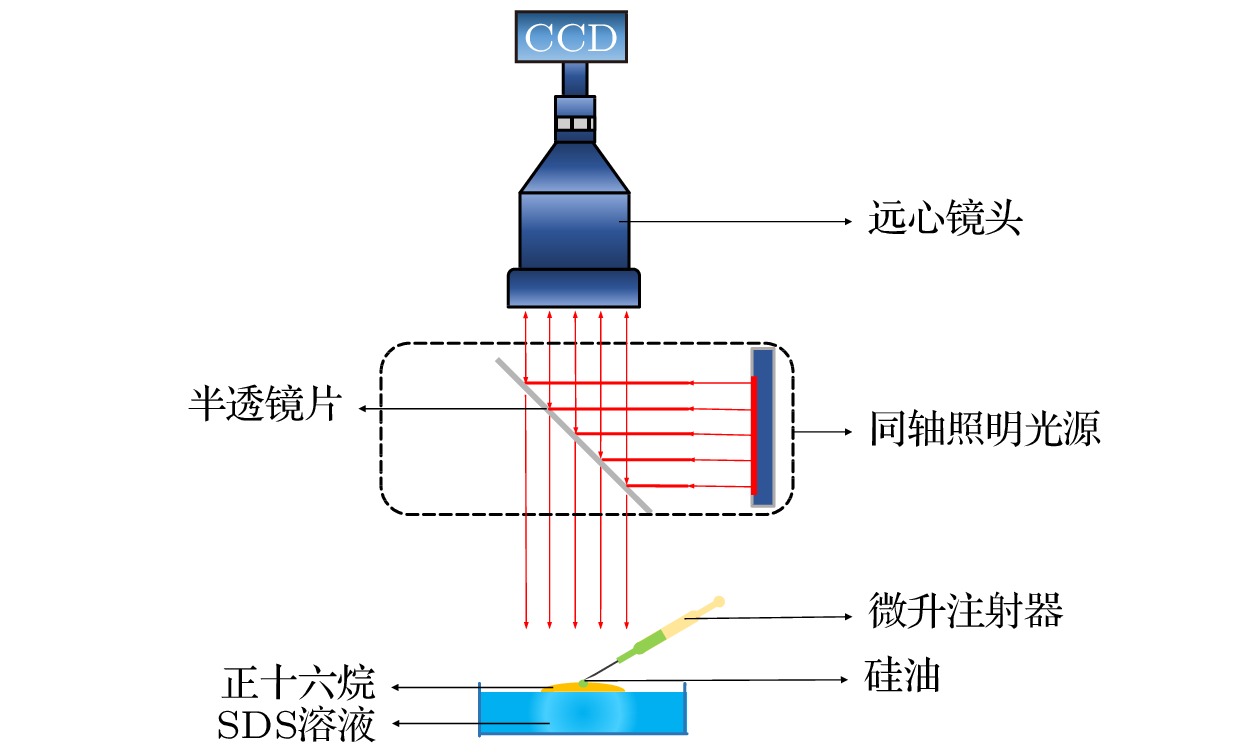
液体表面的液滴运动在微流体和许多生物过程中具有广泛的应用前景. 本文通过研究在液体基底上一种低表面张力液体对另一液体的驱动来理解Marangoni效应在自发驱动体系中的作用. 为了研究液体驱动的液滴铺展过程, 建立了以不易挥发性硅油作为驱动溶剂、正十六烷作为受驱动液滴, 以及不同浓度的十二烷基硫酸钠溶液作为基底溶液的实验体系. 通过对正十六烷液滴受驱动铺展动态过程的观察和研究, 发现界面张力梯度对液体驱动的铺展起主导作用. 实验结果表明: 基底溶液浓度主要对正十六烷液滴的最大铺展半径存在影响. 此外, 用经典稳定性分析模型解释了正十六烷在受驱动铺展过程中由液柱破碎成小液滴的原因, 同时得到了失稳特征参数最快不稳定波长与正十六烷液柱半径之间的关系.

关键词:

Abstract

Drop dynamics at liquid surfaces is existent in nature and industry, which is of great value in studying droplet self-propulsion, surface coating, and drug delivery, and possesses great potential applications in microfluidics and biological process. Here, we analyze the role of Marangoni effect in the spontaneously driving system by studying the driving effect of a low surface tension liquid at the liquid substrate on another liquid. A three-phase liquid system is established to explore the liquid-driven spreading process, including non-volatile silicone oil as driving solvent, n-hexadecane as driven solvent, and sodium dodecyl sulfate (SDS) solution with different concentrations as aqueous substrates. The spreading process of n-hexadecane driven by silicone oil can be divided into two stages. N-hexadecane is first driven to form a thin rim, and then the rim breaks up into small liquid beads. Afterwards, the driving mechanism, spreading scaling laws and instability characteristic parameters of the liquid-driven spreading process are analyzed theoretically. The analysis of driving mechanism indicates that the differences in surface tension among silicone oil, n-hexadecane and SDS solution cause surface tension gradient at the liquid-liquid interface, which plays a crucial role in spreading the n-hexadecane. The results also demonstrate that the maximum spreading radius of n-hexadecane is affected by the concentration of the aqueous substrate. When the concentration of SDS solution is lower than the critical micelle concentration, the maximum spreading radius of n-hexadecane is proportional to the concentration of SDS solution. Meanwhile, the scaling law between the spreading radius R and time t driven by silicone oil conforms to the classical theoretical $ \mathrm{r}\mathrm{e}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\;R\left(t\right)\propto {t}^{3/4} $. In addition, the classical analysis model is used to explain the instability pattern of n-hexadecane breaking into small beads from rim in the liquid-driven spreading process, which is called Rayleigh-Plateau instability. The fastest instability wavelength $ {\lambda }_{\mathrm{s}} $ and the constant radius $ {r}_{\mathrm{c}} $ of the n-hexadecane liquid rim are related by $ {\lambda }_{\mathrm{s}}\approx 9{r}_{\mathrm{c}} $. Our results prove the applicability of the spreading scaling law to the liquid-driven spreading process, and also help to understand in depth the mechanism of the liquid-driven spreading and the instability pattern in the spreading process.

Keywords:

作者及机构信息

1.
青岛理工大学机械与汽车工程学院, 青岛　266520

2.
中国科学院力学研究所, 国家微重力重点实验室, 北京　100190

3.
中国科学院大学工程科学学院, 北京　100049

通信作者: 王进, wangjin@qut.edu.cn ; 蓝鼎, landing@imech.ac.cn ;

基金项目: 山东省重点研发计划(批准号: 2019GGX102023)和国家自然科学基金(批准号: U1738118, 11472275)资助的课题

Authors and contacts

1.
School of Mechanical and Automotive Engineering, Qingdao University of Technology, Qingdao 266520, China

2.
National Microgravity Laboratory, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

3.
School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Wang Jin, wangjin@qut.edu.cn ; Lan Ding, landing@imech.ac.cn ;

Funds: Project supported by the Key R&D Program of Shandong Province, China (Grant No. 2019GGX102023) and the National Natural Science Foundation of China (Grant Nos. U1738118, 11472275)

文章全文 : translate this paragraph

参考文献

[1]	袁泉子, 沈文豪, 赵亚溥 2016 力学进展 46 343 Google Scholar Yuan Q Z, Shen W H, Zhao Y B 2016 Adv. Mech. 46 343 Google Scholar
[2]	Yeo Y, Chen A, Basaran O, Park K 2004 Pharm. Res. 21 1419 Google Scholar
[3]	Charve J, Reineccius G 2009 J. Agric. Food Chem. 57 2486 Google Scholar
[4]	Blanco-Pascual N, Koldeweij R, Stevens R, Montero P, Gomez-Guillen M, Ten Cate A T 2014 Food Bioprocess Technol. 7 2472 Google Scholar
[5]	Zhao X, Kim J, Cezar C, Huebsch N, Lee K, Bouhadir K, Mooney D 2011 Proc. Natl. Acad. Sci. U. S. A. 108 67 Google Scholar
[6]	Seemann R, Fleury J B, Maass C C 2016 Eur. Phys. J.-Spec. Top. 225 2227 Google Scholar
[7]	Kang D, Nadim A, Chugunova M 2017 Phys. Fluids 29 495 Google Scholar
[8]	Roman B, Bico J 2010 J. Phys. Condens. Matter 22 493101 Google Scholar
[9]	Elfring G, Goyal G 2015 J. Non-Newtonian Fluid Mech. 234 8 Google Scholar
[10]	Tanner L H 1979 J. Phys. D; Appl. Phys. 12 13 Google Scholar
[11]	Milchev A, Binder K 2002 J. Chem. Phys. 116 7691 Google Scholar
[12]	Franklin B, Brownrigg W, Farish A 1774 Philos. Trans. R. Soc. Lond 64 445 Google Scholar
[13]	Hoult D P 1972 Annu. Rev. Fluid Mech. 4 341 Google Scholar
[14]	Fraaije J G E M, Cazabat A 1989 J. Colloid Interface Sci. 133 452 Google Scholar
[15]	Berg S 2009 Phys. Fluids 21 398 Google Scholar
[16]	Wodlei F, Sebilleau J, Magnaudet J, Pimienta V 2018 Nat. Commun. 9 820 Google Scholar
[17]	Afsar-Siddiqui A, Luckham P, Matar O 2004 Adv. Colloid Interface Sci. 106 183 Google Scholar
[18]	Lee K S, Starov V 2009 J. Colloid Interface Sci. 329 361 Google Scholar
[19]	Afsar-Siddiqui A, Luckham P, Matar O 2003 Langmuir 19 703 Google Scholar
[20]	Lee K S, Starov V 2007 J. Colloid Interface Sci. 314 631 Google Scholar
[21]	Koldeweij R, Capelleveen B, Lohse D, Visser C W 2019 Soft Matter 15 8525 Google Scholar
[22]	Chengara A, Nikolov A D, Wasan D T 2007 Ind. Eng. Chem. Res. 46 2987 Google Scholar
[23]	Wilkinson K, Bain C, Matsubara H, Aratono M 2005 ChemPhysChem 6 547 Google Scholar
[24]	Bonn D, Ross D 2001 Rep. Prog. Phys. 64 1085 Google Scholar
[25]	Bergeron V, Langevin D 1996 Phys. Rev. Lett. 76 3152 Google Scholar
[26]	Brochardwyart F, Dimeglio J M, Quere D, Degennes P G 1991 Langmuir 7 335 Google Scholar
[27]	Rayleigh J 1878 Proc. London Math. Soc. 10 4 Google Scholar
[28]	Eggers J, Dupont T 2001 J. Fluid Mech. 262 205 Google Scholar
[29]	Frankel I, Weihs D 1987 J. Fluid Mech. 185 361 Google Scholar

施引文献

图 1 实验装置示意图

Fig. 1. Schematic diagram of experimental device.

下载: 全尺寸图片幻灯片

图 2 不同浓度SDS溶液表面正十六烷初始铺展状态(比例尺为2 mm)

Fig. 2. Initial spreading state of n-hexadecane on the surface of SDS solutions with different concentrations (scale bar = 2 mm).

下载: 全尺寸图片幻灯片

图 3 SDS溶液(8 mmol/L)表面正十六烷受驱动铺展过程(比例尺为10 mm)

Fig. 3. Spreading process of n-hexadecane on the surface of SDS solution (8 mmol/L) (scale bar = 10 mm).

下载: 全尺寸图片幻灯片

图 4 硅油的驱动作用示意图. 1, 2和3分别为驱动溶剂硅油、受驱动溶剂正十六烷和基底SDS溶液, $ {\sigma }_{23} $和$ {\sigma }_{12} $分别表示正十六烷与SDS基底溶液之间和硅油与正十六烷之间的界面张力, $ \nabla \sigma $表示界面张力梯度, ${\Delta }P$表示压力梯度

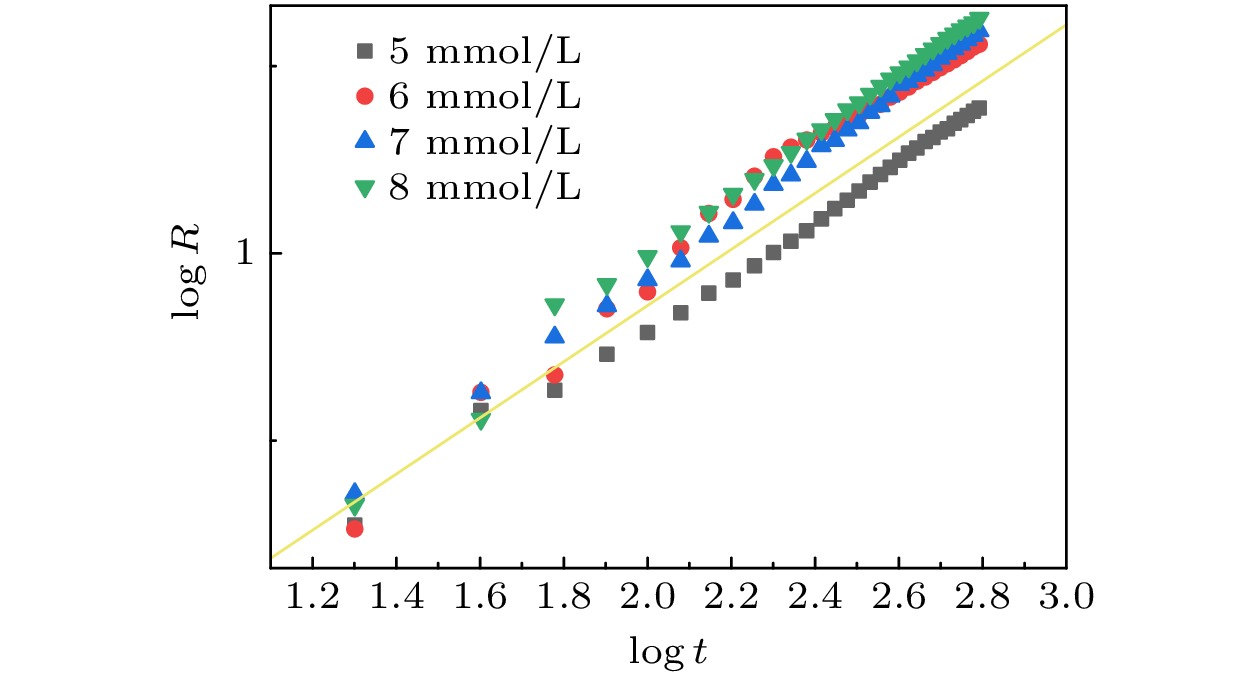
Fig. 4. Schematic diagram of the driving effect of silicone oil. 1, 2 and 3 are driving solvent (silicone oil), driven solvent (n-hexadecane) and aqueous substrate (SDS solution), $ {\sigma }_{23} $ and $ {\sigma }_{12} $ represent the interfacial tension between n-hexadecane and SDS solution and between silicone oil and n-hexadecane, respectively. $ \nabla \sigma $ represents the interfacial tension gradient, and $ {\Delta }P $ represents the pressure gradient.

下载: 全尺寸图片幻灯片

图 5 正十六烷液滴受驱动铺展阶段示意图

Fig. 5. Schematic diagram of the driven-spreading stage of n-hexadecane.

下载: 全尺寸图片幻灯片

图 6 失稳前不同浓度的SDS溶液表面正十六烷铺展半径R随时间的变化(在5, 6, 7和8 mmol/L的SDS溶液表面, 正十六烷受驱动铺展的标度率分别为0.73, 0.80, 0.82, 0.83, 黄线为理论值0.75)

Fig. 6. Variations of the spreading radius R of n-hexadecane on the surface of SDS solutions with different concentrations before instability occurs. The driven-spreading scale rate of n-hexadecane is 0.73, 0.80, 0.82, and 0.83 on the surface of 5, 6, 7 and 8 mmol/L SDS solution, respectively. The yellow line is the theoretical rate of 0.75.

下载: 全尺寸图片幻灯片

表 1 表/界面张力$ \sigma $ (单位: mN·m^–1)

Table 1. Surface/Interfacial tension $ \sigma $ (in mN·m^–1)

SDS溶液浓度/(mmol·L^–1) 5 6 7 8

表面张力 33.19 32.82 32.62 34.53
与正十六烷界面张力 6.52 6.29 6.56 6.60

下载: 导出CSV

表 2 铺展系数S

Table 2. Spreading coefficient S.

SDS溶液浓度/(mmol·L^–1) 5 6 7 8

S –0.13 –0.27 –0.74 1.12

下载: 导出CSV

表 3 增长最快波长$ {\lambda }_{\mathrm{s}} $、半径$ {r}_{\mathrm{c}} $和$ {\lambda }_{\mathrm{s}}/{r}_{\mathrm{c}} $的实验值

Table 3. Experimental values of the fastest growing wavelength $ {\lambda }_{\mathrm{s}} $, the radius $ {r}_{\mathrm{c}} $ and $ {\lambda }_{\mathrm{s}}/{r}_{\mathrm{c}} $.

SDS溶液浓度/(mmol·L^–1) 5 6 7 8

$ {\lambda }_{\mathrm{s}} $/mm 3.38 3.12 3.04 3.79
$ {r}_{\mathrm{c}} $/mm 0.36 0.32 0.31 0.41
$ {\lambda }_{\mathrm{s}}/{r}_{\mathrm{c}} $ 9.39 9.75 9.81 9.24

下载: 导出CSV

map

[1]	袁泉子, 沈文豪, 赵亚溥 2016 力学进展 46 343 Google Scholar Yuan Q Z, Shen W H, Zhao Y B 2016 Adv. Mech. 46 343 Google Scholar
[2]	Yeo Y, Chen A, Basaran O, Park K 2004 Pharm. Res. 21 1419 Google Scholar
[3]	Charve J, Reineccius G 2009 J. Agric. Food Chem. 57 2486 Google Scholar
[4]	Blanco-Pascual N, Koldeweij R, Stevens R, Montero P, Gomez-Guillen M, Ten Cate A T 2014 Food Bioprocess Technol. 7 2472 Google Scholar
[5]	Zhao X, Kim J, Cezar C, Huebsch N, Lee K, Bouhadir K, Mooney D 2011 Proc. Natl. Acad. Sci. U. S. A. 108 67 Google Scholar
[6]	Seemann R, Fleury J B, Maass C C 2016 Eur. Phys. J.-Spec. Top. 225 2227 Google Scholar
[7]	Kang D, Nadim A, Chugunova M 2017 Phys. Fluids 29 495 Google Scholar
[8]	Roman B, Bico J 2010 J. Phys. Condens. Matter 22 493101 Google Scholar
[9]	Elfring G, Goyal G 2015 J. Non-Newtonian Fluid Mech. 234 8 Google Scholar
[10]	Tanner L H 1979 J. Phys. D; Appl. Phys. 12 13 Google Scholar
[11]	Milchev A, Binder K 2002 J. Chem. Phys. 116 7691 Google Scholar
[12]	Franklin B, Brownrigg W, Farish A 1774 Philos. Trans. R. Soc. Lond 64 445 Google Scholar
[13]	Hoult D P 1972 Annu. Rev. Fluid Mech. 4 341 Google Scholar
[14]	Fraaije J G E M, Cazabat A 1989 J. Colloid Interface Sci. 133 452 Google Scholar
[15]	Berg S 2009 Phys. Fluids 21 398 Google Scholar
[16]	Wodlei F, Sebilleau J, Magnaudet J, Pimienta V 2018 Nat. Commun. 9 820 Google Scholar
[17]	Afsar-Siddiqui A, Luckham P, Matar O 2004 Adv. Colloid Interface Sci. 106 183 Google Scholar
[18]	Lee K S, Starov V 2009 J. Colloid Interface Sci. 329 361 Google Scholar
[19]	Afsar-Siddiqui A, Luckham P, Matar O 2003 Langmuir 19 703 Google Scholar
[20]	Lee K S, Starov V 2007 J. Colloid Interface Sci. 314 631 Google Scholar
[21]	Koldeweij R, Capelleveen B, Lohse D, Visser C W 2019 Soft Matter 15 8525 Google Scholar
[22]	Chengara A, Nikolov A D, Wasan D T 2007 Ind. Eng. Chem. Res. 46 2987 Google Scholar
[23]	Wilkinson K, Bain C, Matsubara H, Aratono M 2005 ChemPhysChem 6 547 Google Scholar
[24]	Bonn D, Ross D 2001 Rep. Prog. Phys. 64 1085 Google Scholar
[25]	Bergeron V, Langevin D 1996 Phys. Rev. Lett. 76 3152 Google Scholar
[26]	Brochardwyart F, Dimeglio J M, Quere D, Degennes P G 1991 Langmuir 7 335 Google Scholar
[27]	Rayleigh J 1878 Proc. London Math. Soc. 10 4 Google Scholar
[28]	Eggers J, Dupont T 2001 J. Fluid Mech. 262 205 Google Scholar
[29]	Frankel I, Weihs D 1987 J. Fluid Mech. 185 361 Google Scholar

[1]	张超, 布龙祥, 张智超, 樊朝霞, 凡凤仙. 丁二酸-水纳米气溶胶液滴表面张力的分子动力学研究. , 2023, 72(11): 114701. doi: 10.7498/aps.72.20222371
[2]	黄皓伟, 梁宏, 徐江荣. 表面张力对高雷诺数Rayleigh-Taylor不稳定性后期增长的影响. , 2021, 70(11): 114701. doi: 10.7498/aps.70.20201960
[3]	周浩, 李毅, 刘海, 陈鸿, 任磊生. 最优输运无网格方法及其在液滴表面张力效应模拟中的应用. , 2021, 70(24): 240203. doi: 10.7498/aps.70.20211078
[4]	刘哲, 王雷磊, 时朋朋, 崔海航. 纳米流体液滴内的光驱流动实验及其解析解. , 2020, 69(6): 064701. doi: 10.7498/aps.69.20191508
[5]	张旋, 张天赐, 葛际江, 蒋平, 张贵才. 表面活性剂对气-液界面纳米颗粒吸附规律的影响. , 2020, 69(2): 026801. doi: 10.7498/aps.69.20190756
[6]	沈婉萍, 尤仕佳, 毛鸿. 夸克介子模型的相图和表面张力. , 2019, 68(18): 181101. doi: 10.7498/aps.68.20190798
[7]	艾旭鹏, 倪宝玉. 流体黏性及表面张力对气泡运动特性的影响. , 2017, 66(23): 234702. doi: 10.7498/aps.66.234702
[8]	喻晓, 沈杰, 钟昊玟, 张洁, 张高龙, 张小富, 颜莎, 乐小云. 强脉冲电子束辐照材料表面形貌演化的模拟. , 2015, 64(21): 216102. doi: 10.7498/aps.64.216102
[9]	孙鹏楠, 李云波, 明付仁. 自由上浮气泡运动特性的光滑粒子流体动力学模拟. , 2015, 64(17): 174701. doi: 10.7498/aps.64.174701
[10]	马理强, 苏铁熊, 刘汉涛, 孟青. 微液滴振荡过程的光滑粒子动力学方法数值模拟. , 2015, 64(13): 134702. doi: 10.7498/aps.64.134702
[11]	白玲, 李大鸣, 李彦卿, 王志超, 李杨杨. 基于范德瓦尔斯表面张力模式液滴撞击疏水壁面过程的研究. , 2015, 64(11): 114701. doi: 10.7498/aps.64.114701
[12]	李源, 罗喜胜. 黏性、表面张力和磁场对Rayleigh-Taylor不稳定性气泡演化影响的理论分析. , 2014, 63(8): 085203. doi: 10.7498/aps.63.085203
[13]	宋保维, 任峰, 胡海豹, 郭云鹤. 表面张力对疏水微结构表面减阻的影响. , 2014, 63(5): 054708. doi: 10.7498/aps.63.054708
[14]	苏铁熊, 马理强, 刘谋斌, 常建忠. 基于光滑粒子动力学方法的液滴冲击固壁面问题数值模拟. , 2013, 62(6): 064702. doi: 10.7498/aps.62.064702
[15]	马理强, 常建忠, 刘汉涛, 刘谋斌. 液滴溅落问题的光滑粒子动力学模拟. , 2012, 61(5): 054701. doi: 10.7498/aps.61.054701
[16]	毕菲菲, 郭亚丽, 沈胜强, 陈觉先, 李熠桥. 液滴撞击固体表面铺展特性的实验研究. , 2012, 61(18): 184702. doi: 10.7498/aps.61.184702
[17]	蒋涛, 欧阳洁, 赵晓凯, 任金莲. 黏性液滴变形过程的核梯度修正光滑粒子动力学模拟. , 2011, 60(5): 054701. doi: 10.7498/aps.60.054701
[18]	王晓亮, 陈硕. 液气共存的耗散粒子动力学模拟. , 2010, 59(10): 6778-6785. doi: 10.7498/aps.59.6778
[19]	刘秀梅, 贺杰, 陆建, 倪晓武. 表面张力对固壁旁空泡运动特性影响的理论和实验研究. , 2009, 58(6): 4020-4025. doi: 10.7498/aps.58.4020
[20]	张蜡宝, 代富平, 熊予莹, 魏炳波. 深过冷Ni-15％Sn合金熔体表面张力研究. , 2006, 55(1): 419-423. doi: 10.7498/aps.55.419

计量

文章访问数: 6921
PDF下载量: 192
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于Marangoni效应的液-液驱动铺展过程