-
量子照明雷达旨在利用量子光场探测热噪声环境下低反射率目标是否存在. 发射光源的纠缠特性使其较经典雷达具有独到的探测优势. 纠缠相干态(entangled coherent state, ECS)作为一类在噪声环境下纠缠鲁棒性较强的量子态, 近年来在量子科学的多个领域得到广泛的应用. 本文研究了基于三类不同ECS态的量子照明雷达的目标探测性能, 并以双模压缩态(two-mode squeezed vacuum state, TMSV)和相干态作为基准对比和分析了三类ECS态纠缠度大小与其探测性能之间的关系. 研究发现: 在目标为低反射率且发射光子数远小于背景噪声的情形下, 三类ECS态的探测性能优于相干态, 劣于TMSV态; 此外, 三类ECS态的探测性能可由其纠缠度的大小来决定. 在其他照明条件下, 使用量子照明雷达进行目标探测较相干态雷达并无明显的优势, 三类ECS态的探测性能与TMSV态和相干态方案并无明显联系.There has been a great interest in quantum metrology (e.g., quantum interferometric radar) due to its applications in sub-Rayleigh ranging and remote sensing. Despite interferometric radar has received vast amount of attentions over the past two decades, very few researches has been conducted on another type of quantum radar: quantum illumination radar, or more precisely quantum target detection. It is, in general, used to interrogate whether the low-reflectivity target in a noisy thermal bath is existed using quantum light. The entanglement properties of its emitted light source give it a unique detection advantage over the classical radar. Entangled coherent state (ECS), as a class of quantum states with high entanglement robustness in noisy environments, has been widely used in several fields of quantum science such as quantum informatics, quantum metrology . In this paper, we investigate the target detection performance of quantum illumination radar based on three different types of ECS states. We employ the two-mode squeezed vacuum state (TMSV) and the coherent state as benchmarks to compare and analyze the relationship between the entanglement strength of the three types of ECS states and their quantum illumination detection performance. We found that the detection performance of the three ECS states is better than that of the coherent state. However, it is inferior to that of the TMSV state when the target is of low reflectivity. The emitted photon number is much smaller than the background noise (we call this as “good” illumination conditions). On the contrary, quantum illumination radar has no obvious advantage over coherent state radar for target detection under other illumination conditions; further, the detection performance of these three types of ECS states is not evidently related to that of the TMSV state and the coherent state. Finally, we reveal that the target detection performance of quantum illumination for the first two types of ECS states can be determined by their entanglement strength under “good” illumination conditions by adjusting the inter-modal phase of these two ECS states while keeping the emitted photon number constant. Under other illumination conditions, there is no evidence to demonstrate the entanglement strength of ECS states being associated with their target detection performance.
[1] Lanzagorta M 2011 Quantum Radar (San Rafael: Morgan & Claypool publishers) pp1−2
[2] Pirandola S, Bardhan B R, Gehring T, Weedbrook C, Lloyd S 2018 Nat. Photonics 12 724
Google Scholar
[3] Lloyd S 2008 Science 321 1463
Google Scholar
[4] Shapiro J H 2020 IEEE Aerosp. Electron. Syst. Mag. 35 8
Google Scholar
[5] Tan S H, Erkmen B I, Giovannetti V, Guha S, Lloyd S, Maccone L, Pirandola S, Shapiro J H 2008 Phys. Rev. Lett. 101 253601
Google Scholar
[6] Palma G D, Borregaard J 2018 Phys. Rev. A 98 012101
Google Scholar
[7] Guha S, Erkmen B I 2009 Phys. Rev. A 80 052310
Google Scholar
[8] Zhuang Q, Zhang Z, Shapiro J H 2017 Phys. Rev. Lett. 118 040801
Google Scholar
[9] Dolinar S J 1973 M.I.T. Res. Lab. Electron. Quart. Prog. Rep. 111 115
[10] Zhuang Q, Zhang Z, Shapiro J H 2017 J. Opt. Soc. Am. B 34 1567
Google Scholar
[11] Jo Y, Lee S, Ihn Y S, Kim Z, Lee S Y 2021 Phys. Rev. Research 3 013006
Google Scholar
[12] Zhang Z, Mouradian S, Wong F N C, Shapiro J H 2015 Phys. Rev. Lett. 114 110506
Google Scholar
[13] Lopaeva E D, Ruo Berchera I, Degiovanni I P, Olivares S, Bride G, Genovese M 2013 Phys. Rev. Lett. 110 153603
Google Scholar
[14] England D G, Balaji B, Sussman B J 2019 Phys. Rev. A 99 023828
Google Scholar
[15] Zhang Z, Tengner M, Zhong T, Wong F N C, Shapiro J H 2013 Phys. Rev. Lett. 111 010501
Google Scholar
[16] Cho A https://www.sciencemag.org/news/2020/09/short-weird-life-and-potential-afterlife-quantum-radar [2020-9-23]
[17] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Phys. Rev. Lett. 114 080503
Google Scholar
[18] Chang C W S, Vadiraj A M, Bourassa J, Balaji B, Wilson C M 2019 Appl. Phys. Lett. 114 112601
Google Scholar
[19] Barzanjeh S, Pirandola S, Vitali D, Fink J M 2020 Sci. Adv. 6 eabb0451
Google Scholar
[20] Shapiro J H, Lloyd S 2009 New J. Phys. 11 063045
Google Scholar
[21] Devi A R U, Rajagopal A K 2009 Phys. Rev. A 79 062320
Google Scholar
[22] Fan L F, Zubairy M S 2018 Phys. Rev. A 98 012319
Google Scholar
[23] Zhang Y M, Li X W, Yang W, Jin G R 2013 Phys. Rev. A 88 043832
Google Scholar
[24] Jeong H, Kim M S, Lee J 2001 Phys. Rev. A 64 052308
Google Scholar
[25] Park K, Jeong H 2010 Phys. Rev. A 82 062325
Google Scholar
[26] van Enk S J, Hirota 2001 Phys. Rev. A 64 022313
Google Scholar
[27] Simon D S, Jaeger G, Sergienko A V 2014 Phys. Rev. A 89 012315
Google Scholar
[28] Joo J, Munro W J, Spiller T P 2011 Phys. Rev. Lett. 107 083601
Google Scholar
[29] Joo J, Park K, Jeong H, Munro W J, Nemoto K, Spiller T P 2012 Phys. Rev. A 86 043828
Google Scholar
[30] Lee S Y, Ihn Y S, Kim Z 2020 Phys. Rev. A 101 012332
Google Scholar
[31] Liu J, Lu X M, Sun Z, Wang X 2016 J. Phys. A: Math. Theor. 49 115302
Google Scholar
[32] Helstrom C W 1967 Int. Control 10 254
Google Scholar
[33] Audenaert K M R, Calsamiglia J, Muňoz-Tapia R, Bagan E, Masanes L, Acin A, Verstraete F 2007 Phys. Rev. Lett. 98 160501
Google Scholar
[34] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[35] Weedbrook C, Pirandola S, Thompson J, Vedral V, Gu M 2016 New J. Phys. 18 043027
Google Scholar
[36] Zhang S L, Guo J S, Bao W S, Shi J H, Jin C H, Zou X B, Guo G C 2014 Phys. Rev. A 89 062309
Google Scholar
[37] Zhang S L, Zou X B, Shi J H, Guo J S, Guo G C 2014 Phys. Rev. A 90 052308
Google Scholar
[38] Zhuang Q, Zhang Z, Shapiro J H 2017 Phys. Rev. A 96 020302(R
Google Scholar
[39] Las Heras U, Di Candia R, Fedorov K G, Deppe F, Sanz M, Solano E 2017 Sci. Rep. 7 9333
Google Scholar
-
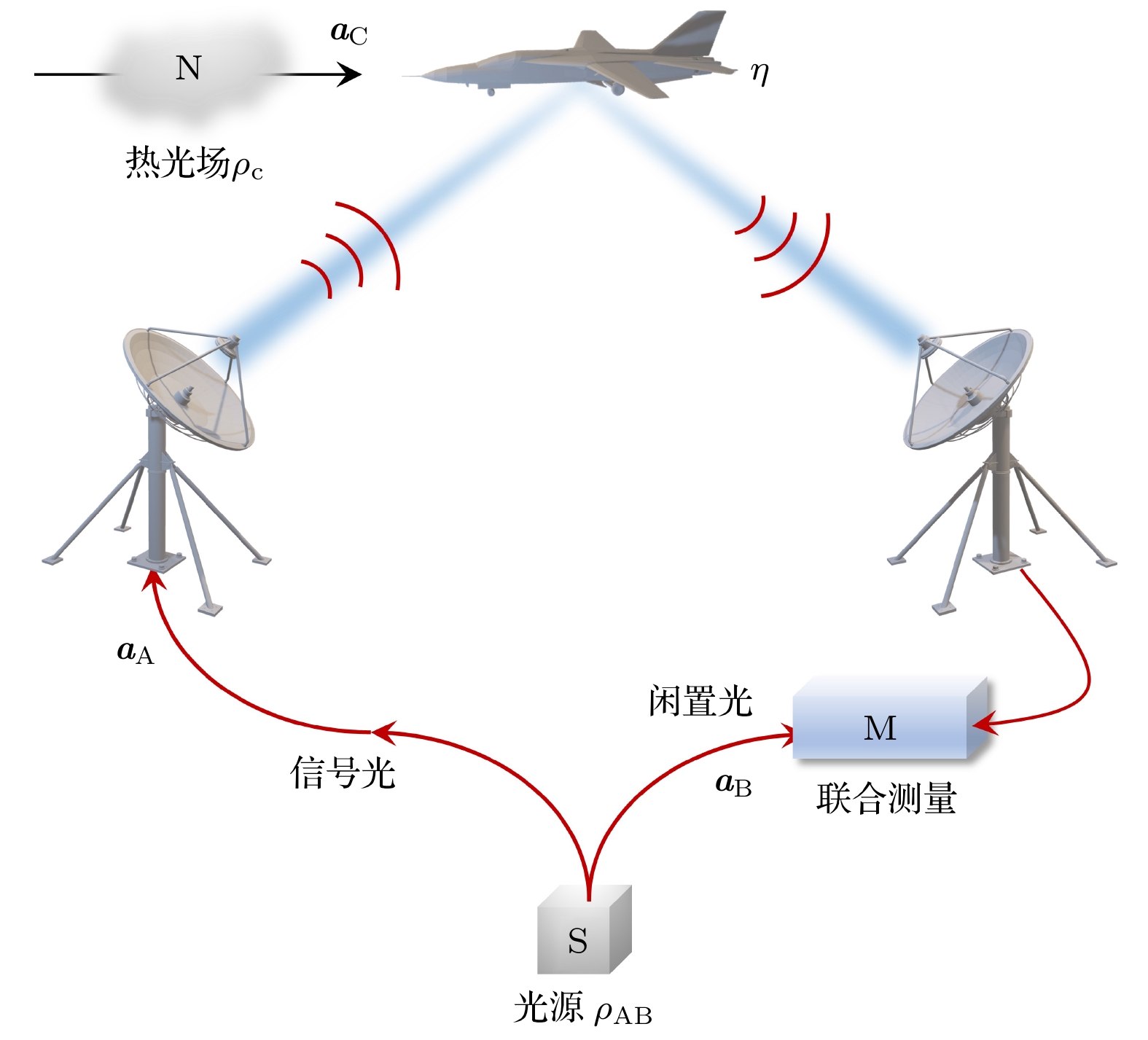
图 1 量子照明雷达的物理模型. 发射光源
$\rho _{\rm {AB}}$ 产生双模纠缠的量子态, A模作为信号光用于审查目标物体(图中用“飞机”代替)是否存在. 若目标存在, 热光场$\rho _{\rm C}$ 与A模在目标物体处进行混合, 随后与留在本地的闲置光B模进行联合测量. 若目标不存在,$\rho _{\rm C}$ 则直接进入探测器与B模进行联合测量Fig. 1. Physical model of quantum illumination radar. The photonic source
$\rho_{\rm {AB}}$ generates two-mode entangled quantum states. Mode A is used as a signal mode to interrogate the presence of the target object (illustrated by “an airplane” in figure). If an object is present, the thermal noise$\rho_{\rm C}$ is mixed with mode A at the object and subsequently measured together with the retained-mode B. If no object is present,$\rho_{\rm C}$ will enter the final measurement device directly for joint quantum measurements with mode B.
图 2 von Neumann熵E随发射光子数
$N_{\rm {emit}}$ 的变化曲线Fig. 2. The variation curve of von Neumann entropy E with the emitted photon number
$N_{\rm {emit}}$ .
图 3 不同热光场光子数下QCB衰减系数ε与Helstrom极限随发射光子数
$N_{\rm {emit}}$ 的变化曲线 (a), (c)$N_{\rm {th}} \!=\! 0.1$ ; (b), (d)$N_{\rm {th}} \!=\! 1$ Fig. 3. Variation curves of QCB attenuation coefficient ε and Helstrom limit with the emitted photon number
$N_{\rm {emit}}$ for different thermal noise photon numbers: (a), (c)$N_{\rm {th}} = 0.1$ ; (b), (d)$N_{\rm {th}} = 1$ .
图 4
$N_{\rm {emit}} = 1$ 时的von Neumann熵E与QCB衰减系数ε随相位φ的变化曲线 (a)von Neumann熵; (b), (c), (d) QCB衰减系数, 其中Nth的值分别为(b)$N_{{\rm{th}}} = 15$ , (c)$N_{{\rm{th}}} = 1$ 以及(d)$N_{{\rm{th}}} = 0.1$ Fig. 4. Variation curves of von Neumann entropy E and QCB attenuation coefficient ε with phase φ for
$N_{\rm {emit}} = 1$ : (a) von Neumann entropy; (b), (c), (d) QCB attenuation coefficient, with (b)$N_{{\rm{th}}} = 15$ , (c)$N_{{\rm{th}}} = 1$ and (d)$N_{{\rm{th}}} = 0.1$ , respectively.
图 5
$N_{\rm {emit}} = 0.3$ 时的QCB衰减系数ε与Helstrom极限随热光场光子数$N_{\rm {th}}$ 的变化曲线Fig. 5. Variation curve of QCB attenuation coefficient ε and Helstrom limit with the thermal noise photon number
$N_{\rm {th}}$ for$N_{\rm {emit}} = 0.3$ . -
[1] Lanzagorta M 2011 Quantum Radar (San Rafael: Morgan & Claypool publishers) pp1−2
[2] Pirandola S, Bardhan B R, Gehring T, Weedbrook C, Lloyd S 2018 Nat. Photonics 12 724
Google Scholar
[3] Lloyd S 2008 Science 321 1463
Google Scholar
[4] Shapiro J H 2020 IEEE Aerosp. Electron. Syst. Mag. 35 8
Google Scholar
[5] Tan S H, Erkmen B I, Giovannetti V, Guha S, Lloyd S, Maccone L, Pirandola S, Shapiro J H 2008 Phys. Rev. Lett. 101 253601
Google Scholar
[6] Palma G D, Borregaard J 2018 Phys. Rev. A 98 012101
Google Scholar
[7] Guha S, Erkmen B I 2009 Phys. Rev. A 80 052310
Google Scholar
[8] Zhuang Q, Zhang Z, Shapiro J H 2017 Phys. Rev. Lett. 118 040801
Google Scholar
[9] Dolinar S J 1973 M.I.T. Res. Lab. Electron. Quart. Prog. Rep. 111 115
[10] Zhuang Q, Zhang Z, Shapiro J H 2017 J. Opt. Soc. Am. B 34 1567
Google Scholar
[11] Jo Y, Lee S, Ihn Y S, Kim Z, Lee S Y 2021 Phys. Rev. Research 3 013006
Google Scholar
[12] Zhang Z, Mouradian S, Wong F N C, Shapiro J H 2015 Phys. Rev. Lett. 114 110506
Google Scholar
[13] Lopaeva E D, Ruo Berchera I, Degiovanni I P, Olivares S, Bride G, Genovese M 2013 Phys. Rev. Lett. 110 153603
Google Scholar
[14] England D G, Balaji B, Sussman B J 2019 Phys. Rev. A 99 023828
Google Scholar
[15] Zhang Z, Tengner M, Zhong T, Wong F N C, Shapiro J H 2013 Phys. Rev. Lett. 111 010501
Google Scholar
[16] Cho A https://www.sciencemag.org/news/2020/09/short-weird-life-and-potential-afterlife-quantum-radar [2020-9-23]
[17] Barzanjeh S, Guha S, Weedbrook C, Vitali D, Shapiro J H, Pirandola S 2015 Phys. Rev. Lett. 114 080503
Google Scholar
[18] Chang C W S, Vadiraj A M, Bourassa J, Balaji B, Wilson C M 2019 Appl. Phys. Lett. 114 112601
Google Scholar
[19] Barzanjeh S, Pirandola S, Vitali D, Fink J M 2020 Sci. Adv. 6 eabb0451
Google Scholar
[20] Shapiro J H, Lloyd S 2009 New J. Phys. 11 063045
Google Scholar
[21] Devi A R U, Rajagopal A K 2009 Phys. Rev. A 79 062320
Google Scholar
[22] Fan L F, Zubairy M S 2018 Phys. Rev. A 98 012319
Google Scholar
[23] Zhang Y M, Li X W, Yang W, Jin G R 2013 Phys. Rev. A 88 043832
Google Scholar
[24] Jeong H, Kim M S, Lee J 2001 Phys. Rev. A 64 052308
Google Scholar
[25] Park K, Jeong H 2010 Phys. Rev. A 82 062325
Google Scholar
[26] van Enk S J, Hirota 2001 Phys. Rev. A 64 022313
Google Scholar
[27] Simon D S, Jaeger G, Sergienko A V 2014 Phys. Rev. A 89 012315
Google Scholar
[28] Joo J, Munro W J, Spiller T P 2011 Phys. Rev. Lett. 107 083601
Google Scholar
[29] Joo J, Park K, Jeong H, Munro W J, Nemoto K, Spiller T P 2012 Phys. Rev. A 86 043828
Google Scholar
[30] Lee S Y, Ihn Y S, Kim Z 2020 Phys. Rev. A 101 012332
Google Scholar
[31] Liu J, Lu X M, Sun Z, Wang X 2016 J. Phys. A: Math. Theor. 49 115302
Google Scholar
[32] Helstrom C W 1967 Int. Control 10 254
Google Scholar
[33] Audenaert K M R, Calsamiglia J, Muňoz-Tapia R, Bagan E, Masanes L, Acin A, Verstraete F 2007 Phys. Rev. Lett. 98 160501
Google Scholar
[34] Wootters W K 1998 Phys. Rev. Lett. 80 2245
Google Scholar
[35] Weedbrook C, Pirandola S, Thompson J, Vedral V, Gu M 2016 New J. Phys. 18 043027
Google Scholar
[36] Zhang S L, Guo J S, Bao W S, Shi J H, Jin C H, Zou X B, Guo G C 2014 Phys. Rev. A 89 062309
Google Scholar
[37] Zhang S L, Zou X B, Shi J H, Guo J S, Guo G C 2014 Phys. Rev. A 90 052308
Google Scholar
[38] Zhuang Q, Zhang Z, Shapiro J H 2017 Phys. Rev. A 96 020302(R
Google Scholar
[39] Las Heras U, Di Candia R, Fedorov K G, Deppe F, Sanz M, Solano E 2017 Sci. Rep. 7 9333
Google Scholar
下载:
计量
- 文章访问数: 7344
- PDF下载量: 299
- 被引次数: 0
