-
The equation of state (EOS) for CH material used as an ablator layer at high pressure is important in the study of implosion dynamics and target design for inertial confinement fusion (ICF). At present, most of EOS data are on the Hugoniot line under shock compression. The EOS data below Hugoniot line need further studying for low-entropy pre- compression. In the present article, the EOS of polystyrene is established under quasi-isentropic compression driven by HEAVEN-I KrF laser facility with a long rising edge (~20 ns). The shock dynamic behaviors of three kinds of CH targets are simulated, which are 100 μm CH planar target, Al-coated CH planar target (10 μm Al, 50 or 150 μm CH), and flyer-impact target composed of flyer (Al-coated CH), 100 μm vacuum layer, and 100 μm CH layer. The planar targets and flyer-impact targets with different thickness are irradiated by six-focused laser beams with total energy of 50–100J, and the free surface velocity and wave average transit velocity are measured by side-on shadowgraph technique. The simulation results indicate that the initial loading process is quasi-isentropic compression process, and then evolves into a weak shock compression process for the CH planar target in the rising edge stage. Comparing with the CH planar target, the reflected rarefaction waves from the Al-CH interface of Al-coated CH target can suppress the enhancement of compression wave, and delay the formation of shock wave when laser directly irradiates the Al layer. The shock pressure of the CH target layer (the third layer) is significantly higher than those of the former two targets in the flyer-impact target. However, the chasing rarefaction wave can unload the compression state incompletely and reduce the pressure when the CH target layer is much thicker than Al layer. The final pressure is about 15 GPa in the CH planar target, while the final pressure is about 30 GPa in flyer-impact target: both of them are less than the pressure threshold of opacity change for the transparent polystyrene. The quasi-isentropic dynamical process is difficult to measure by the velocity interferometer system for any reflector technique. The experimental results show that the average wave transit velocity is significantly less than the final shock velocity derived from the free surface velocities in the CH and Al-coated CH planar target side-on shadow experiments. They indicate that the compression wave enhancement and quasi-isentropic compression process occur in the propagation of wave front. The shock pressure is about 12 GPa in the CH planar target, and about 34 GPa under shock load in the flyer-impact target. The experimental data and shock dynamic processes are basically consistent with the simulation results.
-
Keywords:
- quasi-isentropic compression /
- side-on shadowgraph /
- equation of state /
- shock velocity /
- particle velocity
[1] Lindl J, Landen O, Edwards J, Moses E 2014 Phys. Plasmas 21 020501
Google Scholar
[2] Ma T, Hurricane O A, Callahan D A, et al. 2015 Phys. Rev. Lett. 114 145004
Google Scholar
[3] He X T, Li J W, Fan Z F, Wang L F, Liu J, Lan K, Wu J F, Ye W H 2016 Phys. Plasmas 23 082706
Google Scholar
[4] Campbell E M, Goncharov V N, Sangster T C, et al. 2017 Matter Radiat. Extrem. 2 37
Google Scholar
[5] Barrios M A, Hicks D G, Boehly T R, Fratauduono D E, Eggert J H 2010 Phys. Plasmas 17 056307
Google Scholar
[6] Barrios M A, Boehly T R, Hicks D G, Fratauduono D E, Eggert J H, Collins G W, Meyerhofer D D 2012 J. Appl. Phys. 111 093515
Google Scholar
[7] Aglitskiy Y, Velikovich A L, Karasik M, et al. 2018 Phys. Plasmas 25 032705
Google Scholar
[8] 黄秀光, 傅思祖, 舒桦, 叶君建, 吴江, 谢志勇, 方智恒, 贾果, 罗平庆, 龙滔, 何钜华, 顾援, 王世绩 2010 59 6394
Google Scholar
Huang X G, Fu S Z, Shu H, Ye J J, Wu J, Xie Z Y, Fang Z H, Jia G, Luo P Q, Long T, He J H, Gu Y, Wang S J 2010 Acta Phys. Sin. 59 6394
Google Scholar
[9] Shu H, Huang X G, Ye J J, Wu J, Jia G, Fang Z H, Xie Z Y, Zhou H Z, Fu S Z 2015 Eur. Phys. J. D 69 259
Google Scholar
[10] Bradley D K, Eggert J H, Smith R F, Prisbrey S T, Hicks D G, Braun D G, Biener J, Hamza A, Rudd R E, Collins G 2009 Phys. Rev. Lett. 102 075503
Google Scholar
[11] Smith R F, Eggert J H, Jeanloz R, Duffy T S, Braun D G, Patterson J R, Rudd R E, Biener J, Lazicki A E, Hamza A V, Wang J, Braun T, Benedict L X, Celliers P M, Collins G W 2014 Nature 511 330
Google Scholar
[12] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 67 045202
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 67 045202
Google Scholar
[13] Zhang P L, Tang X Z, Li Y J, Wang Z, Tian B X, Yin Q, Lu Z, Xiang Y H, Gao Z X, Li J 2015 Chin. Phys. Lett. 32 075201
Google Scholar
[14] 张品亮, 王钊, 李宇, 田宝贤, 李业军, 殷倩, 汤秀章 2018 原子能科学技术 52 2038
Google Scholar
Zhang P L, Wang Z, Li Y, Tian B X, Li Y J, Yin Q, Tang X Z 2018 At. Energy Sci. Technol. 52 2038
Google Scholar
[15] 向益淮, 高智星, 佟小惠, 戴辉, 汤秀章, 单玉生 2006 强激光与粒子束 18 795
Xiang Y H, Gao Z X, Tong X H, Dai H, Tang X Z, Shan Y S 2006 High Power Laser Part. Beams 18 795
[16] Zvorykin V D, Lebo I G 1999 Laser Part. Beams 17 69
Google Scholar
[17] 田宝贤, 梁晶, 王钊, 李业军, 汤秀章 2012 原子能科学技术 46 39
Google Scholar
Tian B X, Liang J, Wang Z, Li Y J, Tang X Z 2012 At. Energy Sci. Technol. 46 39
Google Scholar
[18] Larsen J T, Lane S M 1994 J. Quant. Spectrosc. Radiat. Transfer 51 179
Google Scholar
[19] 江少恩, 李三伟 2009 58 8440
Google Scholar
Jiang S E, Li S W 2009 Acta Phys. Sin. 58 8440
Google Scholar
[20] 经福谦 1999 实验物态方程导引 (北京: 科学出版社) 第2, 211页
Jing F Q 1999 Introduction to Experimental Equation of State (Beijing: Science Press) p2, 211 (in Chinese)
[21] Fu S Z, Huang X G, Ma M X, Shu H, Wu J, Ye J J, He J H, Gu Y, Luo P Q, Long T, Zhang Y H 2007 J. Appl. Phys. 101 043517
Google Scholar
-
图 1 CH材料状态方程侧向阴影 (a)实验布局; (b)原理示意图
Fig. 1. CH EOS side-on shadow experiments: (a) experimental layout; (b) schematics.
图 2 (a) “天光一号”的典型脉冲时间波形; (b)六束聚焦叠加光斑的空间分布
Fig. 2. (a) Heaven-I laser pulse shape; (b) spatial profile of six-beam focusing spot.
图 3 CH靶结构示意图 (a)纯CH平面靶; (b) 镀膜CH靶; (c)飞片撞击靶
Fig. 3. Structure schematics of CH targets: (a) Planar CH target without Al foil; (b) planar CH target with Al foil; (c) flyer-impact target.
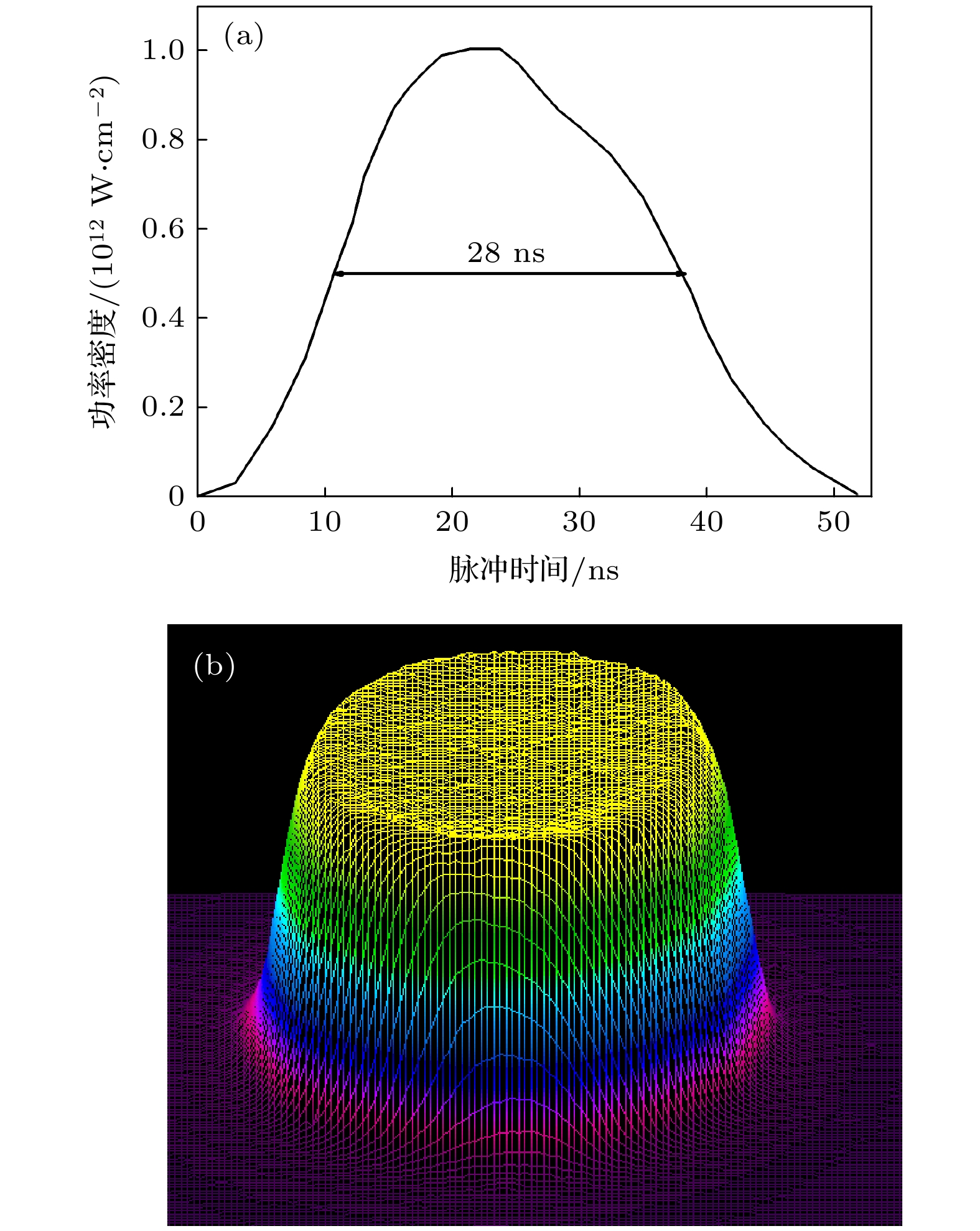
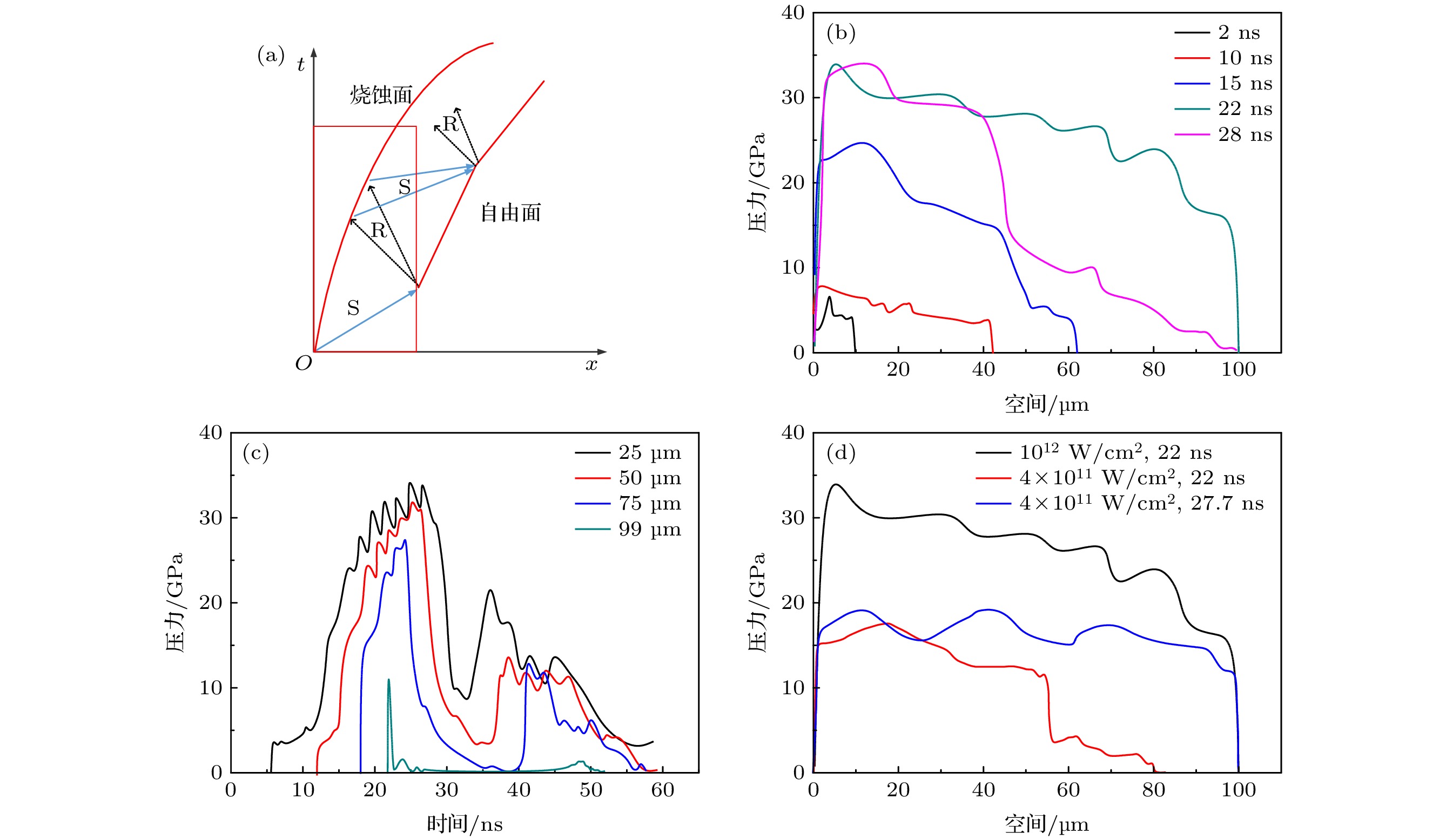
图 4 纯CH平面靶的冲击动力学过程 (a) 冲击波与界面作用的的t-x波系图; (b)不同时刻的压力空间分布; (c)不同膜层的压力加载演化史; (d)不同功率密度下的压力分布
Fig. 4. Shock dynamic processes in CH planar target: (a) t-x schematic diagram of wave propagation; (b) spatial distribution of loading pressure at different time; (c) loading pressure history for different layers; (d) spatial distribution of loading pressure for different laser intensities.
图 5 镀膜CH靶内的冲击动力学过程 (a)冲击波与界面作用的t-x波系图; (b) 阻抗梯度 p-u图; (c) 辐照面为Al层的压力空间分布; (d) 辐照面为CH层的压力空间分布
Fig. 5. Shock dynamic processes in CH planar target coated with Al: (a) t-x schematic diagram of wave propagation; (b) p-u schematic diagram; (c) spatial distribution of loading pressure when laser directly irradiates Al layer; (d) spatial distribution of loading pressure when laser directly irradiates CH film.
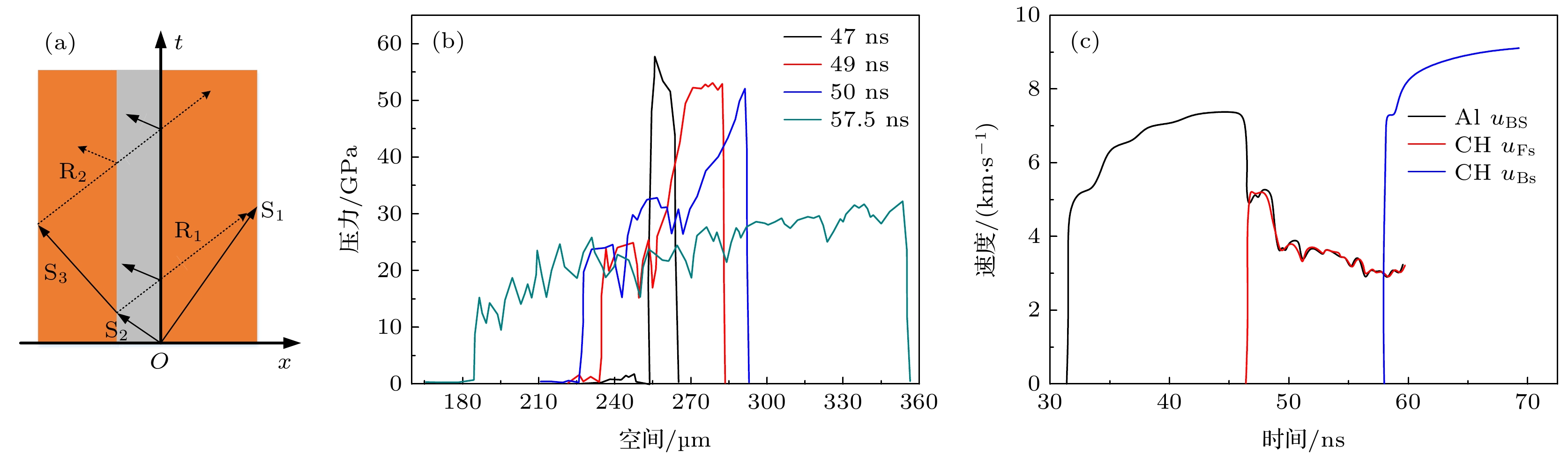
图 6 飞片撞击靶内的冲击动力学过程 (a)靶内冲击波与界面相互作用t-x波系图; (b) 不同时刻靶内加载压力的空间分布; (c) Al层自由面、CH靶前后表面速度曲线
Fig. 6. Shock dynamic processes in flyer-impact target: (a) t-x schematic diagram of wave propagation; (b) space distribution of loading pressure at different time; (c) velocity histories of the back-surface velocity of Al layer (Al uBs), the front-surface (CH uFs) and back-surface (CH uBs) velocities of CH target layer.
图 7 条纹相机侧向阴影动态图像 (a) 纯CH平面靶; (b) Al + CH平面靶; (c)飞片撞击靶
Fig. 7. Side-on shadowgraph images of streak camera: (a) CH planar target; (b) Al + CH planar taget; (c) flyer-impact target.
表 1 HYADES程序输入参数
Table 1. Input parameters of HYADES program.
激光条件 靶结构 靶材料 空间网格 时间步长 波长248 nm 100 μm CH (纯CH) CH: Sesame EOS_32 CH: 1/3 μm 0.1 ns 脉宽28 ns 10 μm Al + 50 μm CH (镀膜CH) Al: Sesame EOS_42 Al: 1/5 μm 波形类高斯 10 μm Al + 150 μm CH (镀膜CH) 功率密度/(1012 W·cm–2) 150 μm CH + 10 μm Al
+ 100 μm vacuum + 100 μm CH (飞片靶)
下载: 导出CSV
表 2 长脉冲激光驱动下的CH靶状态方程数据
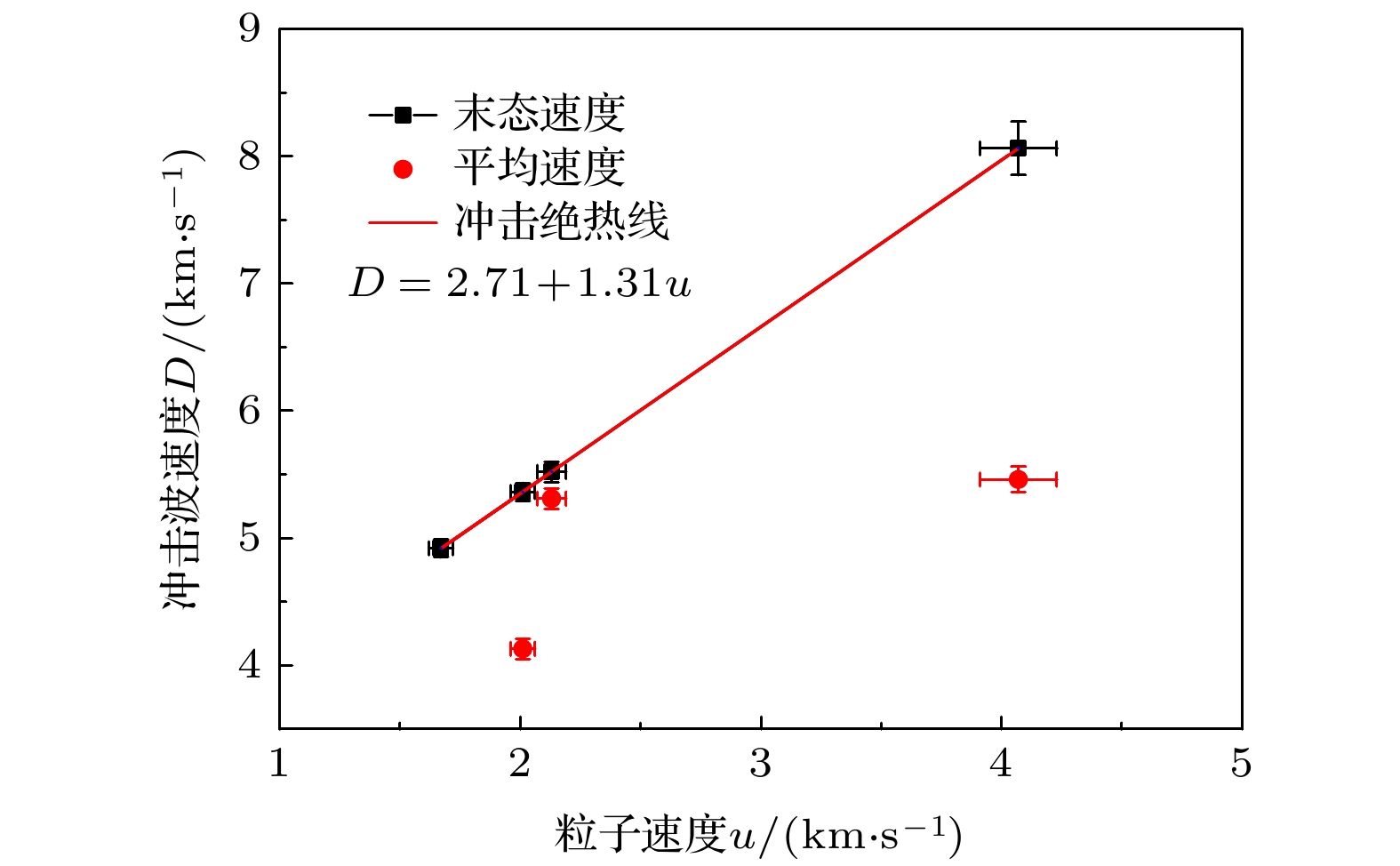
Table 2. EOS parameters of CH target driven by long pulse laser.
靶参数/μm Elaser/J ufs/(km·s–1) uPfs/(km·s–1) Dfs/(km·s–1) Dav/(km·s–1) Pfs/GPa Psim/GPa 180 CH 54 4.26 ± 0.12 2.13 ± 0.06 5.52 ± 0.08 5.31 ± 0.08 12.23 ± 0.39 15.5 110 CH 52.1 4.01 ± 0.10 2.01 ± 0.05 5.36 ± 0.07 4.13 ± 0.08 11.20 ± 0.31 14.1 4.71 Al + 75 CH 72.5 3.34 ± 0.10 1.67 ± 0.05 4.92 ± 0.07 × 8.58 ± 0.38 8.43 150 CH + 10 Al + 空腔 + 100 CH 85 8.14 ± 0.33 4.07 ± 0.16 8.06 ± 0.21 5.46 ± 0.10 34.25 ± 1.61 30.7
下载: 导出CSV
-
[1] Lindl J, Landen O, Edwards J, Moses E 2014 Phys. Plasmas 21 020501
Google Scholar
[2] Ma T, Hurricane O A, Callahan D A, et al. 2015 Phys. Rev. Lett. 114 145004
Google Scholar
[3] He X T, Li J W, Fan Z F, Wang L F, Liu J, Lan K, Wu J F, Ye W H 2016 Phys. Plasmas 23 082706
Google Scholar
[4] Campbell E M, Goncharov V N, Sangster T C, et al. 2017 Matter Radiat. Extrem. 2 37
Google Scholar
[5] Barrios M A, Hicks D G, Boehly T R, Fratauduono D E, Eggert J H 2010 Phys. Plasmas 17 056307
Google Scholar
[6] Barrios M A, Boehly T R, Hicks D G, Fratauduono D E, Eggert J H, Collins G W, Meyerhofer D D 2012 J. Appl. Phys. 111 093515
Google Scholar
[7] Aglitskiy Y, Velikovich A L, Karasik M, et al. 2018 Phys. Plasmas 25 032705
Google Scholar
[8] 黄秀光, 傅思祖, 舒桦, 叶君建, 吴江, 谢志勇, 方智恒, 贾果, 罗平庆, 龙滔, 何钜华, 顾援, 王世绩 2010 59 6394
Google Scholar
Huang X G, Fu S Z, Shu H, Ye J J, Wu J, Xie Z Y, Fang Z H, Jia G, Luo P Q, Long T, He J H, Gu Y, Wang S J 2010 Acta Phys. Sin. 59 6394
Google Scholar
[9] Shu H, Huang X G, Ye J J, Wu J, Jia G, Fang Z H, Xie Z Y, Zhou H Z, Fu S Z 2015 Eur. Phys. J. D 69 259
Google Scholar
[10] Bradley D K, Eggert J H, Smith R F, Prisbrey S T, Hicks D G, Braun D G, Biener J, Hamza A, Rudd R E, Collins G 2009 Phys. Rev. Lett. 102 075503
Google Scholar
[11] Smith R F, Eggert J H, Jeanloz R, Duffy T S, Braun D G, Patterson J R, Rudd R E, Biener J, Lazicki A E, Hamza A V, Wang J, Braun T, Benedict L X, Celliers P M, Collins G W 2014 Nature 511 330
Google Scholar
[12] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 67 045202
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 67 045202
Google Scholar
[13] Zhang P L, Tang X Z, Li Y J, Wang Z, Tian B X, Yin Q, Lu Z, Xiang Y H, Gao Z X, Li J 2015 Chin. Phys. Lett. 32 075201
Google Scholar
[14] 张品亮, 王钊, 李宇, 田宝贤, 李业军, 殷倩, 汤秀章 2018 原子能科学技术 52 2038
Google Scholar
Zhang P L, Wang Z, Li Y, Tian B X, Li Y J, Yin Q, Tang X Z 2018 At. Energy Sci. Technol. 52 2038
Google Scholar
[15] 向益淮, 高智星, 佟小惠, 戴辉, 汤秀章, 单玉生 2006 强激光与粒子束 18 795
Xiang Y H, Gao Z X, Tong X H, Dai H, Tang X Z, Shan Y S 2006 High Power Laser Part. Beams 18 795
[16] Zvorykin V D, Lebo I G 1999 Laser Part. Beams 17 69
Google Scholar
[17] 田宝贤, 梁晶, 王钊, 李业军, 汤秀章 2012 原子能科学技术 46 39
Google Scholar
Tian B X, Liang J, Wang Z, Li Y J, Tang X Z 2012 At. Energy Sci. Technol. 46 39
Google Scholar
[18] Larsen J T, Lane S M 1994 J. Quant. Spectrosc. Radiat. Transfer 51 179
Google Scholar
[19] 江少恩, 李三伟 2009 58 8440
Google Scholar
Jiang S E, Li S W 2009 Acta Phys. Sin. 58 8440
Google Scholar
[20] 经福谦 1999 实验物态方程导引 (北京: 科学出版社) 第2, 211页
Jing F Q 1999 Introduction to Experimental Equation of State (Beijing: Science Press) p2, 211 (in Chinese)
[21] Fu S Z, Huang X G, Ma M X, Shu H, Wu J, Ye J J, He J H, Gu Y, Luo P Q, Long T, Zhang Y H 2007 J. Appl. Phys. 101 043517
Google Scholar
下载:
计量
- 文章访问数: 4367
- PDF下载量: 70
- 被引次数: 0
