-
声空化机械效应是聚焦超声治疗的重要物理机制. 以脂类包膜微泡/纳米相变液滴为空化核可显著地增强空化效应, 本文耦合空化动力学、组织和脂类包膜黏弹性模型, 构建了组织内脂类包膜微泡声空化动力学模型, 数值分析了微泡声空化动力学行为以及周围组织内机械应力的时空分布规律, 并探究了包膜材料、组织黏弹性和驱动声压等关键参数的影响. 包膜和组织黏弹性都将抑制微泡振动, 但组织黏弹性的抑制作用更大. 组织内机械应力在膨胀阶段为挤压应力, 而在收缩阶段和反弹初始阶段为拉伸应力, 且应力局部分布于微泡壁附近, 随着距离增大而显著减小, 其中拉伸应力衰减率明显更大. 包膜黏弹性可减小应力, 但声压较大时, 应力减小可忽略不计. 应力随着组织弹性增大而减小, 随着组织黏度增大而先增大后减小, 随着声压增大而增大. 本研究可为进一步阐释聚焦超声治疗中组织机械损伤的内在机制奠定重要理论基础.Ultrasound-induced cavitation in the viscoelastic biological tissues has attracted considerable attention due to its mechanical bio-effects, such as cell sonoporation, hemolysis, vascular disruption and tissue erosion. Cavitation can exert strong mechanical stresses on the surrounding tissues during the rapid bubble growth and collapse. The occurrence of cavitation needs the ultrasound exposure exceeding a certain acoustic pressure threshold, and the cavitation threshold is very high in most tissues, probably causing undesirable side-effects. Introducing artificial cavitation nuclei, e.g., microbubbles and nanodroplets stabilized with a shell such as albumin, lipids or polymers, into the targeted region can effectively reduce the cavitation threshold and significantly enhance the cavitation effects. However, neither the cavitation dynamics of an encapsulated microbubble nor the cavitation-induced stress field around the bubble in a soft tissue is quite clear. In this study, a comprehensive numerical model is developed to describe the dynamics of a lipid-shelled microbubble in vivo and quantify the cavitation-induced mechanical stress in the tissue. Considering the nonlinear changes of both shell viscosity and elasticity, a Gilmore model that has been considered as the most developed and realistic cavitation model is coupled with the Zener viscoelastic model for precisely describing tissue viscoelastic behavior with both creep recovery and stress relaxation of tissue. The developed model has an advantage of accurately describing the bubble behaviors in different biological tissues at high ultrasound intensities, especially for the bubble collapse. Furthermore, the spatiotemporal evolution of mechanical stress in the surrounding tissue generated by the cavitation bubble is investigated. Finally, the effects of encapsulated shell, elasticity modulus and viscosity of tissue as well as ultrasound amplitude are examined. The results show that the viscoelasticity of encapsulated shell and tissue both inhibit the bubble oscillations, and the tissue viscoelasticity has a larger inhibition effect. During the bubble oscillation, the compressive (negative) stress is generated in the tissue with the bubble growing and it continuously increases until it reaches a maximum value at a maximum radius, while the tensile (positive) stress is generated at the stage of bubble collapse and initial stage of bubble rebound due to the restoration of deformed tissue. The stress magnitude is greatest near the bubble wall and decreases rapidly with depth extending into the surrounding tissue. By contrast, the tensile stress decreases at a higher rate than the compressive stress. The encapsulated bubble presents a smaller stress in the tissue, but the decrease of the stress can be ignored at large acoustic pressures. Moreover, the stress decreases with the increase of tissue elasticity modulus, whereas it first increases and then decreases with tissue viscosity increasing, showing a maximum at 15 mPa·s. The increasing of the ultrasound amplitude enhances the bubble oscillations and consequently increases the stress in the tissue. This study is helpful in understanding the bubble dynamics and cavitation-induced mechanical stress of an encapsulated microbubble in soft tissue, which is essential for a safe and precise ultrasound therapy.
-
Keywords:
- bubble dynamics /
- encapsulated microbubble /
- acoustic cavitation in soft tissue /
- mechanical effect of cavitation
[1] Brennen C E 2014 Cavitation and Bubble Dynamics (London: Cambridge University Press) pp7, 8
[2] Wan M X, Feng Y, Haar G T 2015 Cavitation in Biomedicine: Principles and Techniques (Netherlands: Springer) pp1−3
[3] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第8, 9页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp8, 9 (in Chinese)
[4] Wang M, Zhang Y, Cai C, Tu J, Guo X, Zhang D 2018 Sci. Rep. 8 3885
Google Scholar
[5] Yang Y, Li Q, Guo X, Tu J, Zhang D 2020 Ultrason. Sonochem. 67 105096
Google Scholar
[6] Ho Y, Chang Y, Yeh C 2016 Theranostics 6 392
Google Scholar
[7] Qiu W B, Bouakaz A, Konofagou E E, Zheng H R 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 6
Google Scholar
[8] Qin D, Zhang L, Chang N, Ni P, Zong Y, Bouakaz A, Wan M, Feng Y 2018 Ultrason. Sonochem. 47 141
Google Scholar
[9] 郑海荣, 邱维宝, 王丛知, 牛丽丽, 严飞, 蔡飞燕, 邹超, 隆晓菁, 乔阳紫, 肖杨 2020 中国科学: 生命科学 50 1256
Google Scholar
Zheng H R, Qiu W B, Wang C Z, Niu L L, Yan F, Cai F Y, Zou C, Long X J, Qiao Y Z, Xiao Y 2020 Sci. Sin. Vitae 50 1256
Google Scholar
[10] Xu Z, Fowlkes J B, Rothman E D, Levin A M, Cain C A 2005 J. Acoust. Soc. Am. 117 424
Google Scholar
[11] Mancia L, Vlaisavljevich E, Xu Z, Johnsen E 2017 Ultrasound Med. Biol. 43 1421
Google Scholar
[12] Estrada J B, Barajas C, Henann D L, Johnsen E, Franck C 2018 J. Mech. Phys. Solids 112 291
Google Scholar
[13] Mancia L, Vlaisavljevich E, Yousefi N, Rodriguez M, Ziemlewicz T J, Lee F T, Henann D, Franck C, Xu Z, Johnsen E 2019 Phys. Med. Biol. 64 225001
Google Scholar
[14] Vlaisavljevich E, Maxwell A, Mancia L, Johnsen E, Cain C, Xu Z 2016 Ultrasound Med. Biol. 42 2466
Google Scholar
[15] Dollet B, Marmottant P, Garbin V 2019 Annu. Rev. Fluid Mech. 51 331
Google Scholar
[16] Yang X, Church C C 2005 J. Acoust. Soc. Am. 118 3595
Google Scholar
[17] Hua C, Johnsen E 2013 Phys. Fluids 25 083101
Google Scholar
[18] Zilonova E, Solovchuk M, Sheu T 2018 Ultrason. Sonochem. 40 900
Google Scholar
[19] Pahk K J, Andrade M O, Gélat P, Kim H, Saffari N 2019 Ultrason. Sonochem. 53 164
Google Scholar
[20] Kwan J J, Graham S, Myers R, Carlisle R, Stride E, Coussios C C 2015 Phys. Rev. E 92 023019
Google Scholar
[21] Kooiman K, Roovers S, Langeveld S A, Kleven R T, Dewitte H, O'Reilly M A, Escoffre J M, Bouakaz A, Verweij M D, Hynynen K, Lentacker I, Stride E, Holland C K 2020 Ultrasound Med. Biol. 46 1296
Google Scholar
[22] Chabouh G, Dollet B, Quilliet C, Coupier G 2021 J. Acoust. Soc. Am. 149 1240
Google Scholar
[23] Doinikov A A, Bouakaz A 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 58 981
Google Scholar
[24] 梁金福, 陈伟中, 邵纬航, 周超, 杜联芳, 金利芳 2013 62 084708
Google Scholar
Liang J F, Chen W Z, Shao W H, Zhou C, Du L F, Jin L F 2013 Acta Phys. Sin. 62 084708
Google Scholar
[25] Helfield B 2019 Ultrasound Med. Biol. 45 282
Google Scholar
[26] Versluis M, Stride E, Lajoinie G, Dollet B, Segers T 2020 Ultrasound Med. Biol. 46 2117
Google Scholar
[27] 赵丽霞, 王成会, 莫润阳 2021 70 014301
Zhao L X, Wang C H, Mo R Y 2021 Acta Phys. Sin. 70 014301
[28] Jong N D, Emmer M, Chin C T, Bouakaz A, Mastik F, Lohse D, Versluis M 2007 Ultrasound Med. Biol. 33 653
Google Scholar
[29] Marmottant P, Meer S, Emmer M, Versluis M, Jong N D, Hilgenfeldt S, Lohse D 2005 J. Acoust.Soc.Am. 118 3499
Google Scholar
[30] Meer S M, Dollet B, Voormolen M M, Chin C T, Bouakaz A, Jong N D, Versluis M, Lohse D 2007 J. Acoust.Soc.Am. 121 648
Google Scholar
[31] Doinikov A A, Haac J F, Dayton P A 2009 Ultrasonics 49 269
Google Scholar
[32] Li Q, Matula T J, Tu J, Guo X, Zhang D 2013 Phys. Med. Biol. 58 985
Google Scholar
[33] 郭各朴, 张春兵, 屠娟, 章东 2015 64 114301
Google Scholar
Guo G P, Zhang C B, Tu J, Zhang D 2015 Acta Phys. Sin. 64 114301
Google Scholar
[34] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[35] Warnez M T, Johnsen E 2015 Phys. Fluids 27 063103
Google Scholar
[36] Qin S, Ferrara K W 2010 J. Acoust. Soc. Am. 128 1511
Google Scholar
[37] Ghalichi F, Behnia S, Mottaghi F, Yahyavi M 2020 Phys. Scripta 95 085215
Google Scholar
[38] Vlaisavljevich E, Kim Y, Owens G, Roberts W, Cain C, Xu Z 2013 Phys. Med. Biol. 59 253
-
图 1 黏弹性组织内微泡动力学与应力示意图
Fig. 1. Schematic of the bubble dynamics and stress in the viscoelastic tissue.
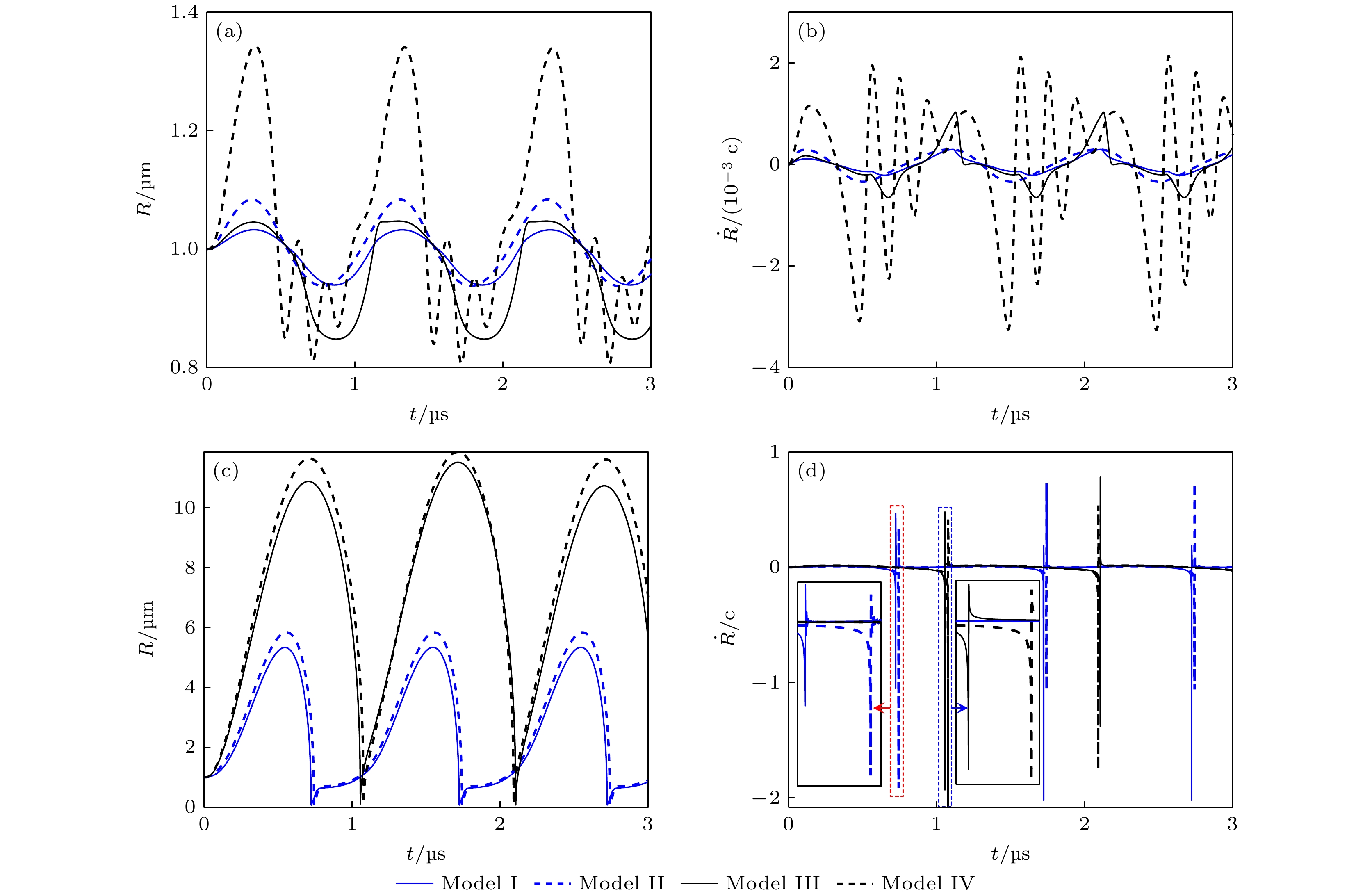
图 2 不同条件下微泡声空化动力学行为 (a), (b)和(c), (d)分别表示pA为0.1 和1 MPa时, 微泡半径和振动速度随时间的变化曲线. I—IV分别表示组织内(I)脂类和(II)无包膜微泡、水中(III)脂类和(IV)无包膜微泡声空化动力学模型
Fig. 2. Bubble dynamics under different conditions. Panels (a), (b) and (c), (d) show the bubble radius and bubble wall velocity at pA = 0.1 MPa and pA = 1 MPa, respectively. The model I and II simulate a shelled microbubble and a clean microbubble oscillating in soft tissue, while the model III and IV in liquid water.
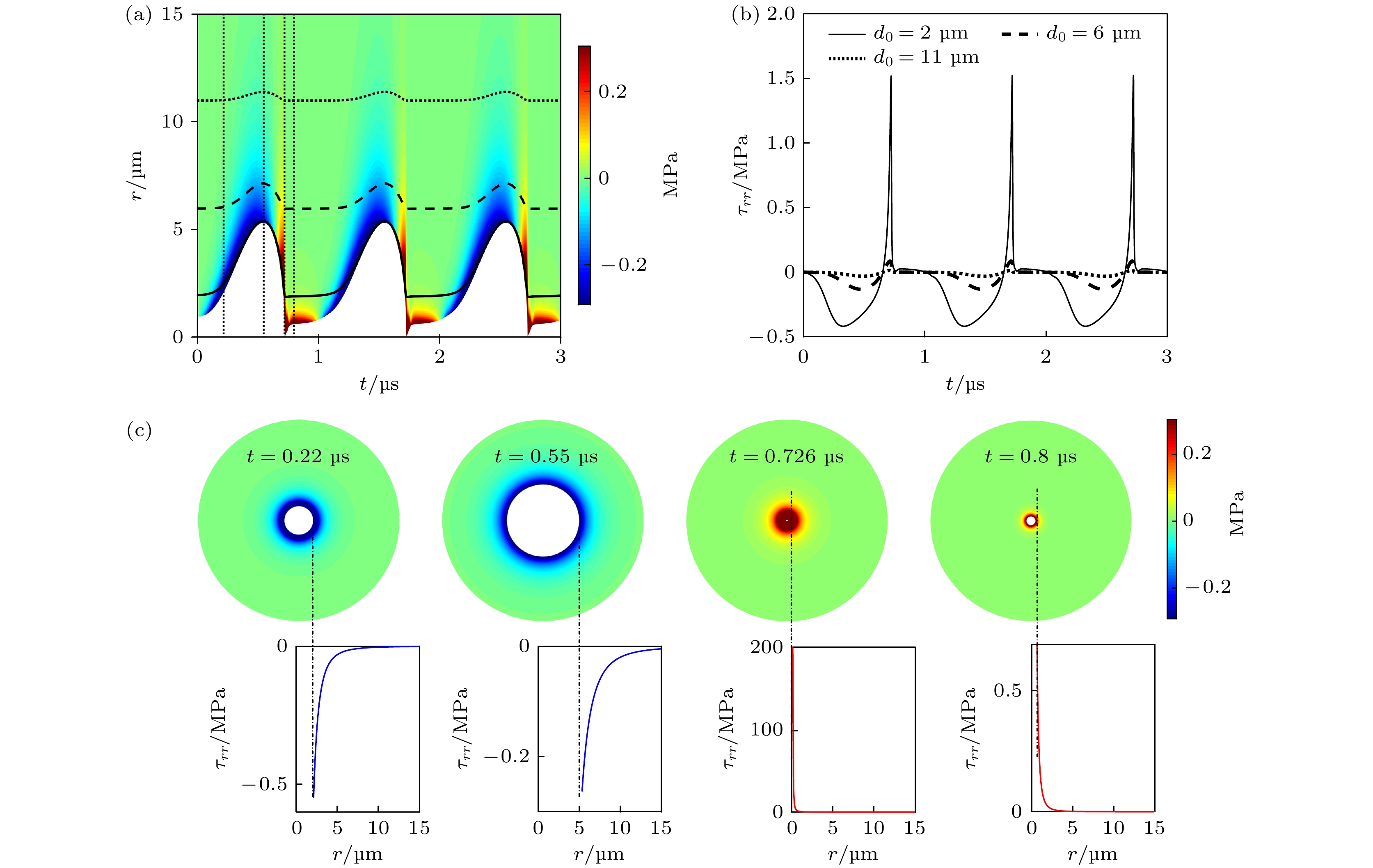
图 3 组织内微泡声空化过程中, 微泡周围组织内机械应力的时间演化和空间分布 (a)微泡声空化动力学与组织内应力的时空分布, 实线、虚线和点线分别为d0 = 2, 6和11 μm粒子的运动轨迹; (b) 3个粒子所受应力随时间的变化曲线; (c)不同时刻(图(a)中点线所示)组织内应力的空间分布, 蓝色和红色实线分别表示挤压应力和拉伸应力
Fig. 3. Temporal and spatial evolution of the mechanical stress distribution during acoustic cavitation in the tissue: (a) The bubble dynamics and spatiotemporal stress distribution, in which solid line, dashed line and dotted line correspond to the trajectories starting at 2, 6 and 11 μm from the bubble center, respectively; (b) the stress magnitudes as a function of time along each trajectory; (c) the stress distribution at the fixed times as indicated by vertical dotted lines in panel (a), with traces indicating the magnitudes of compressive stresses (solid blue) and tensile stresses (solid red).
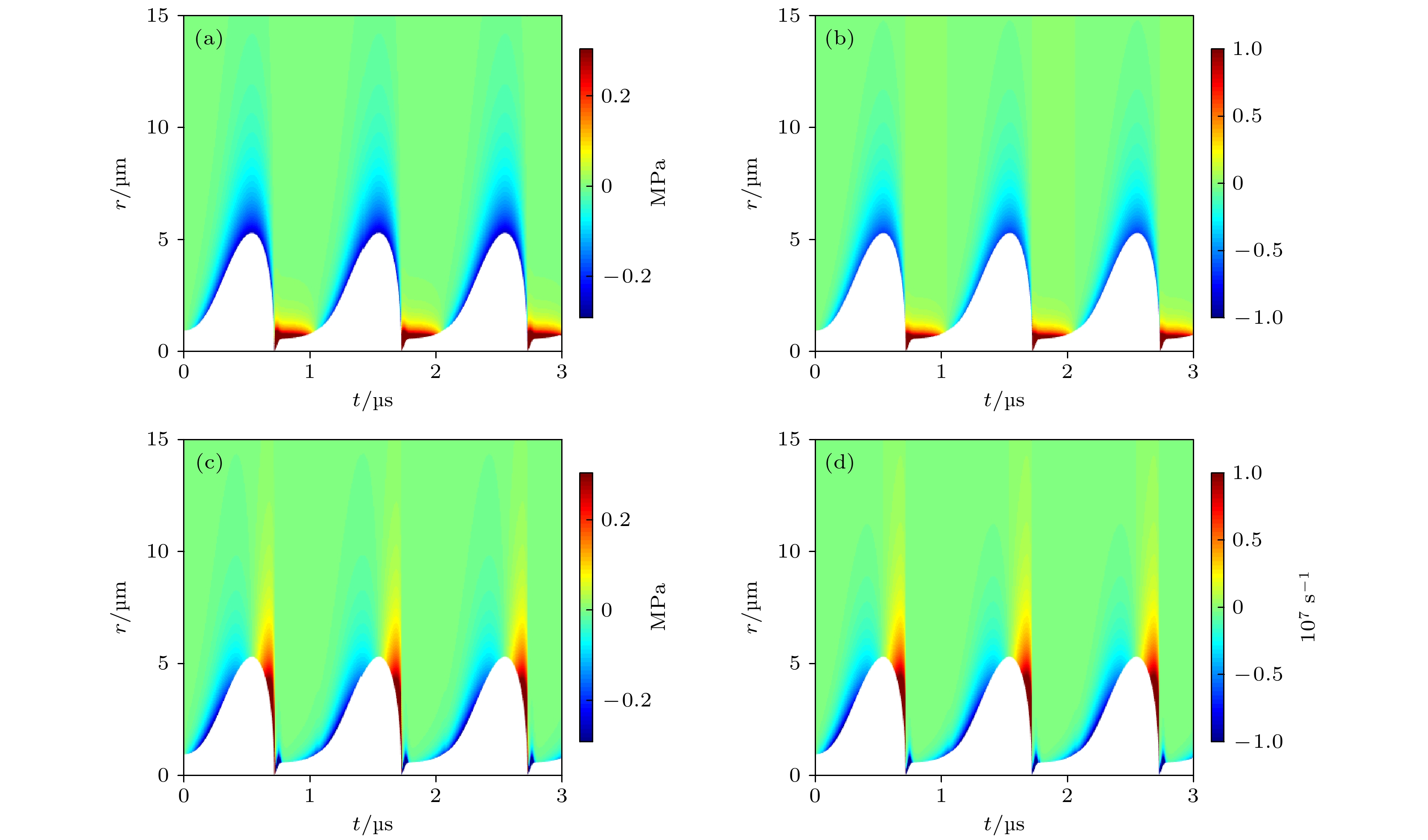
图 4 组织内微泡声空化过程中(a)弹性应力
$ {\tau }_{rr}^{\mathrm{E}} $ 和(b)组织应变γrr的时间演化与空间分布, 以及(c)黏性应力$ {\tau }_{rr}^{\mathrm{v}} $ 和(d)组织应变率$ {\dot{\gamma }}_{rr} $ 的时间演化与空间分布Fig. 4. Temporal and spatial evolution of the (a) elastic stress
$ {\tau }_{rr}^{\mathrm{E}} $ and (b) strain γrr in the tissue; the temporal and spatial evolution of (c) the viscous stress$ {\tau }_{rr}^{\mathrm{v}} $ and (d) strain rate$ {\dot{\gamma }}_{rr} $ , respectively.
图 5 微泡包膜对声空化动力学和组织内应力的影响, 包括pA = 0.1 MPa时, 组织内(a)无包膜微泡和(b)脂类包膜微泡的声空化动力学以及微泡周围应力的时空分布; pA = 1 MPa时, 组织内(d)无包膜微泡和(e)脂类包膜微泡的声空化动力学以及微泡周围应力的时空分布; (c)和(f)表示对应的最大挤压应力和最大拉伸应力随d0的变化曲线
Fig. 5. Effects of bubble shell on the bubble dynamics and stress distributions in the tissues, including (a) the clean bubble and (b) shelled bubble at pA = 0.1 MPa, (d) the clean bubble and (e) shelled bubble at pA = 1 MPa; panels (c) and (f) show the corresponding maximum compressive stresses and tensile stresses, respectively.
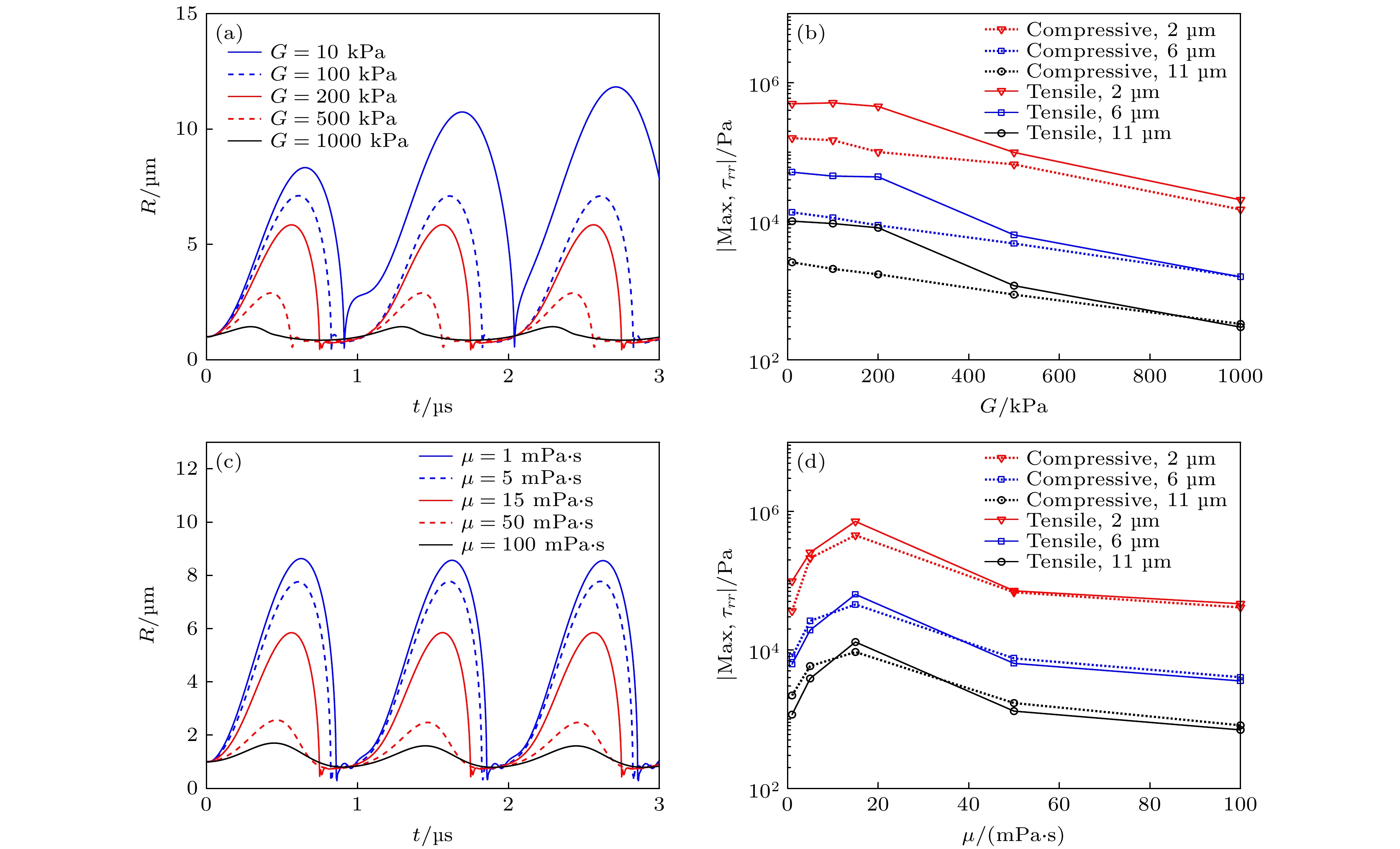
图 6 (a)不同组织弹性模量(G = 10, 100, 200, 500和1000 kPa)下, 组织内微泡半径随时间的变化关系, (b)组织内不同d0处(2, 6和11 μm)粒子所受最大挤压应力和最大拉伸应力随组织弹性模量G的变化关系; (c)不同组织黏度(μ = 1, 5, 15, 50和100 mPa·s)下, 组织内微泡半径随时间的变化关系, (d)组织内不同d0处(2, 6和11 μm)粒子所受最大挤压应力和最大拉伸应力随组织黏度μ的变化关系
Fig. 6. (a) Bubble radius as a function of time, (b) maximum compressive and tensile stresses at different distances (d0 = 2, 6 and 11 μm) in tissues under different shear moduli (G = 10, 100, 200, 500 and 1000 kPa); (c) the bubble radius as a function of time, (d) maximum compressive and tensile stresses at different distances (d0 = 2, 6 and 11 μm) in tissues under different viscosities (μ = 1, 5, 15, 50 and 100 mPa·s).
图 7 (a)不同超声声压(0.1—5 MPa)下, 微泡半径R随时间的变化关系; (b)微泡最大半径Rmax、最小半径Rmin和微泡膨胀-压缩比ΔR+/ΔR– (见插图)随超声声压的变化关系; 组织内不同d0处(2, 6和11 μm)粒子所受(c)最大挤压应力和(d)最大拉伸应力随超声声压的变化关系
Fig. 7. (a) Bubble radius as a function of time at different ultrasound pressures (0.1−5 MPa); (b) the maximum bubble radius Rmax, minimum bubble radius Rmin and the ratio ΔR+/ΔR– of the positive and negative radius excursions as a function of ultrasound pressure; (c) maximum compressive stresses and (d) maximum tensile stresses in tissues at three distances (d0 = 2, 6 and 11 μm) as a function of ultrasound pressure.
-
[1] Brennen C E 2014 Cavitation and Bubble Dynamics (London: Cambridge University Press) pp7, 8
[2] Wan M X, Feng Y, Haar G T 2015 Cavitation in Biomedicine: Principles and Techniques (Netherlands: Springer) pp1−3
[3] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第8, 9页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp8, 9 (in Chinese)
[4] Wang M, Zhang Y, Cai C, Tu J, Guo X, Zhang D 2018 Sci. Rep. 8 3885
Google Scholar
[5] Yang Y, Li Q, Guo X, Tu J, Zhang D 2020 Ultrason. Sonochem. 67 105096
Google Scholar
[6] Ho Y, Chang Y, Yeh C 2016 Theranostics 6 392
Google Scholar
[7] Qiu W B, Bouakaz A, Konofagou E E, Zheng H R 2020 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 68 6
Google Scholar
[8] Qin D, Zhang L, Chang N, Ni P, Zong Y, Bouakaz A, Wan M, Feng Y 2018 Ultrason. Sonochem. 47 141
Google Scholar
[9] 郑海荣, 邱维宝, 王丛知, 牛丽丽, 严飞, 蔡飞燕, 邹超, 隆晓菁, 乔阳紫, 肖杨 2020 中国科学: 生命科学 50 1256
Google Scholar
Zheng H R, Qiu W B, Wang C Z, Niu L L, Yan F, Cai F Y, Zou C, Long X J, Qiao Y Z, Xiao Y 2020 Sci. Sin. Vitae 50 1256
Google Scholar
[10] Xu Z, Fowlkes J B, Rothman E D, Levin A M, Cain C A 2005 J. Acoust. Soc. Am. 117 424
Google Scholar
[11] Mancia L, Vlaisavljevich E, Xu Z, Johnsen E 2017 Ultrasound Med. Biol. 43 1421
Google Scholar
[12] Estrada J B, Barajas C, Henann D L, Johnsen E, Franck C 2018 J. Mech. Phys. Solids 112 291
Google Scholar
[13] Mancia L, Vlaisavljevich E, Yousefi N, Rodriguez M, Ziemlewicz T J, Lee F T, Henann D, Franck C, Xu Z, Johnsen E 2019 Phys. Med. Biol. 64 225001
Google Scholar
[14] Vlaisavljevich E, Maxwell A, Mancia L, Johnsen E, Cain C, Xu Z 2016 Ultrasound Med. Biol. 42 2466
Google Scholar
[15] Dollet B, Marmottant P, Garbin V 2019 Annu. Rev. Fluid Mech. 51 331
Google Scholar
[16] Yang X, Church C C 2005 J. Acoust. Soc. Am. 118 3595
Google Scholar
[17] Hua C, Johnsen E 2013 Phys. Fluids 25 083101
Google Scholar
[18] Zilonova E, Solovchuk M, Sheu T 2018 Ultrason. Sonochem. 40 900
Google Scholar
[19] Pahk K J, Andrade M O, Gélat P, Kim H, Saffari N 2019 Ultrason. Sonochem. 53 164
Google Scholar
[20] Kwan J J, Graham S, Myers R, Carlisle R, Stride E, Coussios C C 2015 Phys. Rev. E 92 023019
Google Scholar
[21] Kooiman K, Roovers S, Langeveld S A, Kleven R T, Dewitte H, O'Reilly M A, Escoffre J M, Bouakaz A, Verweij M D, Hynynen K, Lentacker I, Stride E, Holland C K 2020 Ultrasound Med. Biol. 46 1296
Google Scholar
[22] Chabouh G, Dollet B, Quilliet C, Coupier G 2021 J. Acoust. Soc. Am. 149 1240
Google Scholar
[23] Doinikov A A, Bouakaz A 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 58 981
Google Scholar
[24] 梁金福, 陈伟中, 邵纬航, 周超, 杜联芳, 金利芳 2013 62 084708
Google Scholar
Liang J F, Chen W Z, Shao W H, Zhou C, Du L F, Jin L F 2013 Acta Phys. Sin. 62 084708
Google Scholar
[25] Helfield B 2019 Ultrasound Med. Biol. 45 282
Google Scholar
[26] Versluis M, Stride E, Lajoinie G, Dollet B, Segers T 2020 Ultrasound Med. Biol. 46 2117
Google Scholar
[27] 赵丽霞, 王成会, 莫润阳 2021 70 014301
Zhao L X, Wang C H, Mo R Y 2021 Acta Phys. Sin. 70 014301
[28] Jong N D, Emmer M, Chin C T, Bouakaz A, Mastik F, Lohse D, Versluis M 2007 Ultrasound Med. Biol. 33 653
Google Scholar
[29] Marmottant P, Meer S, Emmer M, Versluis M, Jong N D, Hilgenfeldt S, Lohse D 2005 J. Acoust.Soc.Am. 118 3499
Google Scholar
[30] Meer S M, Dollet B, Voormolen M M, Chin C T, Bouakaz A, Jong N D, Versluis M, Lohse D 2007 J. Acoust.Soc.Am. 121 648
Google Scholar
[31] Doinikov A A, Haac J F, Dayton P A 2009 Ultrasonics 49 269
Google Scholar
[32] Li Q, Matula T J, Tu J, Guo X, Zhang D 2013 Phys. Med. Biol. 58 985
Google Scholar
[33] 郭各朴, 张春兵, 屠娟, 章东 2015 64 114301
Google Scholar
Guo G P, Zhang C B, Tu J, Zhang D 2015 Acta Phys. Sin. 64 114301
Google Scholar
[34] 于洁, 郭霞生, 屠娟, 章东 2015 64 094306
Google Scholar
Yu J, Guo X S, Tu J, Zhang D 2015 Acta Phys. Sin. 64 094306
Google Scholar
[35] Warnez M T, Johnsen E 2015 Phys. Fluids 27 063103
Google Scholar
[36] Qin S, Ferrara K W 2010 J. Acoust. Soc. Am. 128 1511
Google Scholar
[37] Ghalichi F, Behnia S, Mottaghi F, Yahyavi M 2020 Phys. Scripta 95 085215
Google Scholar
[38] Vlaisavljevich E, Kim Y, Owens G, Roberts W, Cain C, Xu Z 2013 Phys. Med. Biol. 59 253
下载:
计量
- 文章访问数: 6066
- PDF下载量: 225
- 被引次数: 0
