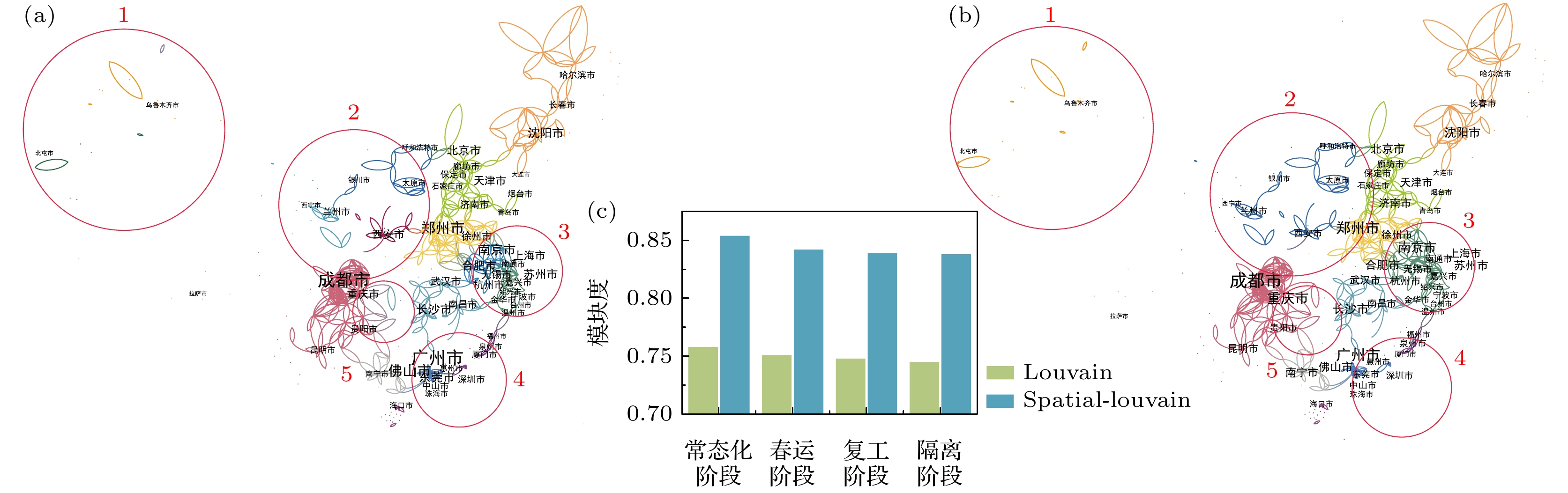
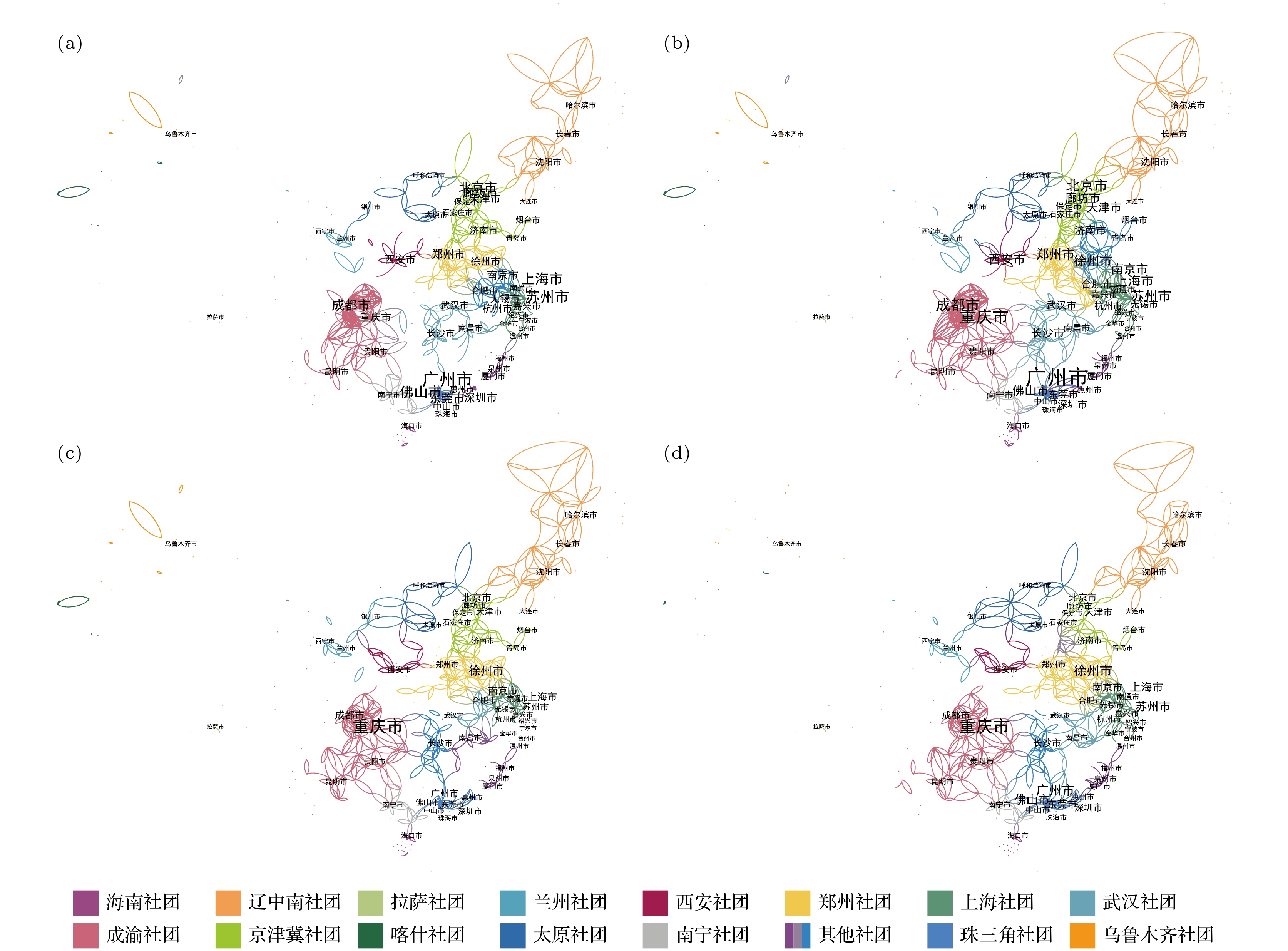
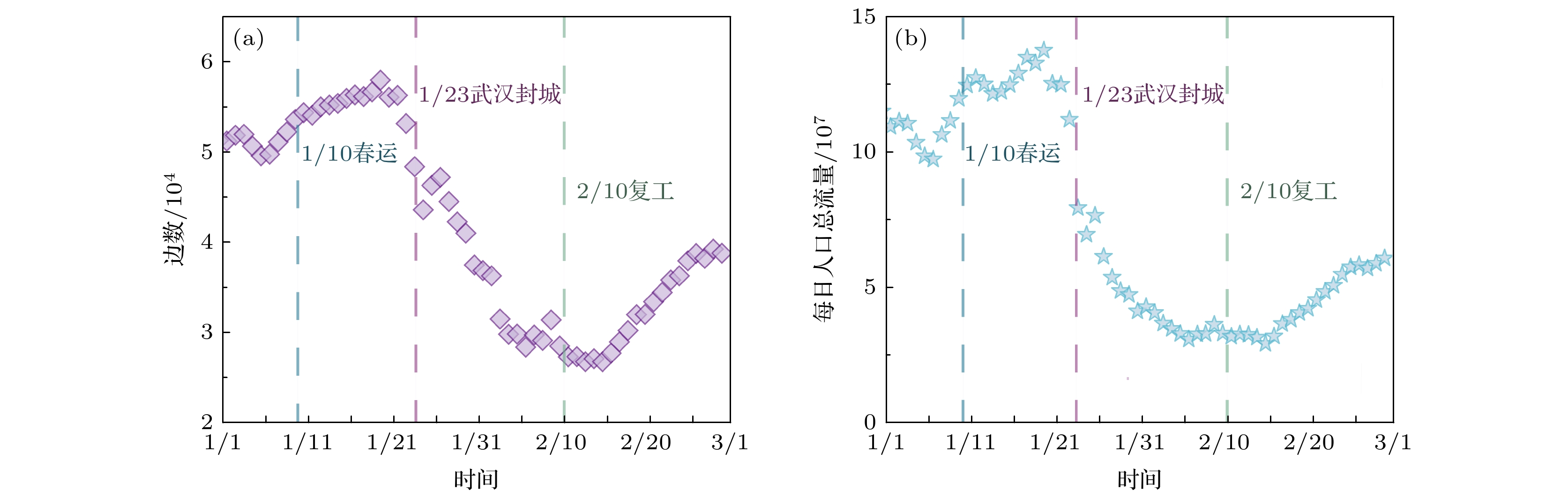
-
新型冠状病毒感染的肺炎(COVID-19)可通过人员接触与流动迅速传播, 因此研究人类迁徙和出行模式的变化对疫情防控至关重要. 本文基于手机运营商2020年春运及疫情暴发前后连续两个月的全国地级市之间的人口流动数据, 运用时序网络分析方法构建人口流动网络拓扑结构指标, 并通过引入地理衰减因子提出Spatial-Louvain社团检测算法, 研究平时、春运、疫情防控隔离和生产复工四阶段的人口迁徙模式的时空演化规律. 研究发现: 受各地疫情防控措施影响, 武汉封城后全国城市间人口流量急剧下降, 并持续至2月中旬. 疫情期间人口流动网络结构呈现四阶段的时空演化模式; 本文提出的空间网络社团检测算法比传统Louvain算法平均模块度值提高了14%; 中国城市分布以经济交互和地理位置为基础, 形成了以核心城市为中心, 向周边辐射的城市群格局; 疫情因素仅能在短暂时间内改变部分城市的城市群归属, 当该因素消失或减弱后, 城市群能迅速恢复原有格局.Population migration is an essential medium for the spread of epidemic, which can accelerate localized outbreaks of disease into widespread epidemic. Large-scale population movements between different areas increase the risk of cross-infection and bring great challenges to epidemic prevention and control. As COVID-19 can spread rapidly through human-to-human transmission, understanding its migration patterns is essential to modeling its spreading and evaluating the efficiency of mitigation policies applied to COVID-19. Using nationwide mobile phone data to track population flows throughout China at prefecture-level, we use the temporal network analysis to compare topological metrics of population mobility network during two consecutive months between before and after the outbreak, i.e. January 1st to February 29th. To detect the regions which are closely connected with population movements, we propose a Spatial-Louvain algorithm through adapting a gravity attenuation factor. Moreover, our proposed algorithm achieves an improvement of 14% in modularity compared with the Louvain algorithm. Additionally, we divide the period into four stages, i.e. normal time, Chunyun migration, epidemic interventions, and recovery time, to describe the patterns of mobility network’s evolution. Through the above methods, we explore the evolution pattern and spatial mechanism of the population mobility from the perspective of spatiotemporal big data and acquire some meaningful findings. Firstly, we find that after the lockdown of Wuhan and effective epidemic interventions, a substantial reduction in mobility lasted until mid-February. Secondly, based on the economic interaction and geographic location, China has formed an urban agglomeration structure with core cities centering and radiating toward the surroundings. Thirdly, in the extreme cases, the dominant factor of population mobility in remote areas is geographic location rather than economy. Fourthly, the urban agglomeration structure of cities is robust so that when the epidemic weakens or disappears, the city clusters can quickly recover into their original patterns.
-
Keywords:
- COVID-19 /
- mobile big data /
- population flow /
- spatio-temporal evolution
[1] Halloran M E, Vespignani A, Bharti N, Feldstein L R, Alexander K, Ferrari M, Shaman J, Drake J M, Porco T, Eisenberg J N 2014 Science 346 433
Google Scholar
[2] Jia J S, Lu X, Yuan Y, Xu G, Jia J, Christakis N A 2020 Nature 582 389
Google Scholar
[3] Colizza V, Barrat A, Barthélemy M, Vespignani A 2006 Proc. Natl. Acad. Sci. U.S.A. 103 2015
Google Scholar
[4] Li Q, Guan X H, Wu P, Wang X Y, Zhou L, Tong Y Q, Ren R Q, Leung S, Lau E, Wong J, Xing X S, Xiang N J, Wu Y, Li C, Chen Q, Li D, Liu T, Zhao J, Li M, Tu W X, Chen C D, Jin L M, Yang R, Wang Q, Zhou S H, Wang R, Liu H, Luo Y B, Liu Y, Shao G, Li H, Tao Z F, Yang Y, Deng Z Q, Liu B X, Ma Z T, Zhang Y P, Shi G Q, Lam T, Wu J, Gao G, Cowling B, Yang B, Leung G, Feng Z J 2020 N. Engl. J. Med. 382 1199
Google Scholar
[5] Guan W J, Ni Z Y, Hu Y, Liang W H, Ou C Q, He J X, Liu L, Shan H, Lei C L, Hui D S 2020 N. Engl. J. Med. 382 1708
Google Scholar
[6] Liu Y X, Yang Y, Zhang C, Huang F M, Wang F X, Yuan J, Wang Z Q, Li J X, Li J M, Feng C 2020 Sci. China, Ser. C Life Sci. 63 364
Google Scholar
[7] Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, Lu X, Zhang W 2020 J. Evid.-Based Med. 13 3
Google Scholar
[8] 栾荣生, 王新, 孙鑫, 陈兴蜀, 周涛, 刘权辉, 吕欣, 吴先萍, 谷冬晴, 唐明霜, 崔慧杰, 单雪峰, 欧阳净, 张本, 张伟 2020 四川大学学报(医学版) 51 131
Google Scholar
Luan R S, Wang X, Sun X, Zhou T, Liu Q H, Lu X, Wu X P, Gu D Q, Tang M S, Cui H J, Shan X F, Ouyang J, Zhang B, Zhang W 2020 J. Sichuan.Univ. 51 131
Google Scholar
[9] 周涛, 刘权辉, 杨紫陌, 廖敬仪, 杨可心, 白薇, 吕欣, 张伟 2020 中国循证医学杂志 20 359
Google Scholar
Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, Lu X, Zhang W 2020 J. Evid.-Based Dent. Pract. Med. China 20 359
Google Scholar
[10] 谭索怡, 曹自强, 秦烁, 陈洒然, 赛斌, 郭淑慧, 刘楚楚, 蔡梦思, 周涛, 张伟, 吕欣 2020 电子科技大学学报 49 788
Google Scholar
Tan S Y, Cao Z Q, Qin S, Chen S R, Sai B, Guo S H, Liu C C, Cai M S, Zhou T, Zhang W, Lu X 2020 J. Univ. Electron. Sci. Technol. China 49 788
Google Scholar
[11] 魏永越, 卢珍珍, 杜志成, 张志杰, 赵杨, 沈思鹏, 王波, 郝元涛, 陈峰 2020 中华流行病学杂志 41 470
Google Scholar
Wei Y Z, Lu Z Z, Du Z C, Zhang Z J, Zhao Y, Shen S P, Wang B, Hao Y T, Chen F 2020 Chinese J. Epidemiology 41 470
Google Scholar
[12] Cohen J 2020 https://www.sciencemag.org/news/2020/02/scientists-are-racing-model-next-moves-coronavirus-thats-stillhard-predict [2021-1-11]
[13] Brockmann D, Helbing D 2013 Science 342 1337
Google Scholar
[14] Wu J T, Leung K, Leung G M 2020 The Lancet 395 689
Google Scholar
[15] 王聪, 严洁, 王旭, 李敏 2020 69 080701
Google Scholar
Wang C, Yan J, Wang X, Li M 2020 Acta Phys. Sin. 69 080701
Google Scholar
[16] Gross B, Zheng Z, Liu S, Chen X, Sela A, Li J, Li D, Havlin S 2020 arXiv: 2003. 08382 [Statistical Physics]
[17] 许小可, 文成, 张光耀, 孙皓宸, 刘波, 王贤文 2020 电子科技大学学报 49 324
Google Scholar
Xu X K, Wen C, Sun G Y, Sun H C, Liu B, Wang X W 2020 J. Univ. Electron. Sci. Technol. China 49 324
Google Scholar
[18] Tian H Y, Liu Y H, Li Y D, Wu C H, Chen B, Kraemer M U, Li B Y, Cai J, Xu B, Yang Q Q 2020 Science 368 638
Google Scholar
[19] Xu C H, Yu Y G, Yang Q C, Lu Z Z 2020 arXiv: 2004. 12541 [physics. soc-ph]
[20] Bengtsson L, Gaudart J, Lu X, Moore S, Wetter E, Sallah K, Rebaudet S, Piarroux R 2015 Sci. Rep. 5 8923
Google Scholar
[21] Wilson R, Erbach S E, Albert M, Power D, Tudge S, Gonzalez M, Guthrie S, Chamberlain H, Brooks C, Hughes C 2016 PLoS. Curr. 1 8
Google Scholar
[22] Lu X, Bengtsson L, Holme P 2012 Proc. Natl. Acad. Sci. U.S.A. 109 11576
Google Scholar
[23] 中华人民共和国工业和信息化部无线电管理局 (miit.gov.cn) https://www.miit.gov.cn/jgsj/wgj/gzdt/art/2020/art_87ace87acac0426a99f4213e4d578cac.html [2021-1-11]
[24] 中华人民共和国工业和信息化部无线电管理局 (miit.gov.cn) https://www.miit.gov.cn/jgsj/wgj/gggs/art/2020/art_9212747d4c794f919bd4aa03a4ca2fcf.html [2021-1-11]
[25] Holme P, Saramaki J 2012 Phys. Rep. 519 97
Google Scholar
[26] Fortunato S 2010 Phys. Rep. 486 75
Google Scholar
[27] Zipf G K 1946 Am. Sociol. Rev. 11 677
Google Scholar
[28] Blondel V D, Guillaume J L, Renaud L, Etienne L 2008 J. Stat. Mech.: Theory Exp. 10 P10008
Google Scholar
[29] Newman M E J 2004 Phys. Rev. E 70 056131
Google Scholar
[30] 新一线城市研究所 (yicai.com) https://www.maigoo.com/news/550235.html [2021-1-11]
[31] Barbosa H, Barthelemy M, Ghoshal G, James C R, Lenormand M, Louail T, Menezes R, Ramasco J J, Simini F, Tomasini M 2018 Phys. Rep. 734 1
Google Scholar
-
图 1 (a) 人口流动网络边数时序特征; (b) 人口总流量时序特征
Fig. 1. (a) Temporal characteristics of the number of edges in the population mobility network; (b) temporal characteristics of total population flow.
图 2 人口流动网络中心性指标时序特征 (a) 平均度; (b) 介数; (c) 接近中心性; (d) 加权度; (e) 网络密度; (f) 集聚系数
Fig. 2. Temporal characteristics of population mobility network centrality metrics: (a) Average degree; (b) betweenness centrality; (c) closeness centrality; (d) weighted degree; (e) density; (f) clustering coefficient.
图 3 SL算法与Louvain算法的人口流动网络社团检测结果对比 (a) SL算法社团检测结果; (b) Louvain算法社团检测结果; (c) 模块度值
Fig. 3. Comparison between SL algorithm and Louvain algorithm: (a) Results of SL; (b) results of Louvain; (c) modularity value.
图 4 基于人口流动网络的四阶段城市集群演化 (a) 常态化阶段; (b) 春运阶段; (c) 隔离阶段; (d)复工阶段
Fig. 4. Four-stage evolution of urban agglomeration based on population mobility network: (a) Normal times; (b) chunyun migration; (c) epidemic interventions; (d) recovery times
图 5 基于人口流动网络的四阶段城市集群演化桑基图
Fig. 5. Sankey diagram of four-stage evolution of urban agglomeration based on population mobility network.
表 1 网络中心性指标
Table 1. Network centrality metrics
中心性指标 公式 描述 度 $k_{i} = \displaystyle\sum\nolimits_{j = 1}^{N} a_{ij}$ N为网络节点总数, $a_{ij}$表示节点i与节点j之间的连接, 如果连接存在, 则$a_{ij} = 1$; 否则$a_{ij} = 0$. 加权度 $k_{i}^{w} =\displaystyle \sum\nolimits_{j = 1}^{N} w_{ij}$ $w_{ij}$表示节点i与节点j之间的连接权值, 在本文中指两个城市间的人口流动数量. 密度 $\rho = \dfrac{M}{N(N-1)}$ M为网络中实际存在的边数, N为节点总数. 该指标用来衡量网络疏密. 集聚系数 $C_{i} = \dfrac{T(i)}{k_{i}\left(k_{i}-1\right)-2 k_{i}^{-1} }$ 其中$T(i)$是经过节点i的有向三角形的数量, $k_{i}$是节点i的入度和出度之和, $k_{i}^{-1}$是$k_{i}$的倒数. 介数 $B_{i}^{w} = \displaystyle\sum\limits_{s \neq i \neq t} \frac{\sigma_{st}(i)}{\sigma_{st} }$ $\sigma_{s t}$为从节点s到节点t的最短路径数量, $\sigma_{s t}(i)$为从节点s到节点t并且经过节点i的最短路径数量. 接近中心性 $C_{i} = \dfrac{N}{\displaystyle\sum\nolimits_{j = 1}^{N} {\rm {dis} }_{ij} }$ N为节点总数, ${\rm {dis}}_{ij}$为节点i到节点j的距离. 
下载: 导出CSV
表 2 人口流动网络四阶段网络基础特征
Table 2. Basic characteristics of the population mobility network in four stages.
网络密度 时间 边数 平均日流量 平均度 图密度 集聚系数 常态化 1.1—1.9 83918 107060322 255.016 0.625 0.779 春运 1.10—1.23 93591 125834714 255.016 0.697 0.818 居家隔离 1.24—2.10 84969 46081244 231.523 0.633 0.775 复工 2.11—2.29 77009 44067415 209.834 0.573 0.738
下载: 导出CSV
-
[1] Halloran M E, Vespignani A, Bharti N, Feldstein L R, Alexander K, Ferrari M, Shaman J, Drake J M, Porco T, Eisenberg J N 2014 Science 346 433
Google Scholar
[2] Jia J S, Lu X, Yuan Y, Xu G, Jia J, Christakis N A 2020 Nature 582 389
Google Scholar
[3] Colizza V, Barrat A, Barthélemy M, Vespignani A 2006 Proc. Natl. Acad. Sci. U.S.A. 103 2015
Google Scholar
[4] Li Q, Guan X H, Wu P, Wang X Y, Zhou L, Tong Y Q, Ren R Q, Leung S, Lau E, Wong J, Xing X S, Xiang N J, Wu Y, Li C, Chen Q, Li D, Liu T, Zhao J, Li M, Tu W X, Chen C D, Jin L M, Yang R, Wang Q, Zhou S H, Wang R, Liu H, Luo Y B, Liu Y, Shao G, Li H, Tao Z F, Yang Y, Deng Z Q, Liu B X, Ma Z T, Zhang Y P, Shi G Q, Lam T, Wu J, Gao G, Cowling B, Yang B, Leung G, Feng Z J 2020 N. Engl. J. Med. 382 1199
Google Scholar
[5] Guan W J, Ni Z Y, Hu Y, Liang W H, Ou C Q, He J X, Liu L, Shan H, Lei C L, Hui D S 2020 N. Engl. J. Med. 382 1708
Google Scholar
[6] Liu Y X, Yang Y, Zhang C, Huang F M, Wang F X, Yuan J, Wang Z Q, Li J X, Li J M, Feng C 2020 Sci. China, Ser. C Life Sci. 63 364
Google Scholar
[7] Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, Lu X, Zhang W 2020 J. Evid.-Based Med. 13 3
Google Scholar
[8] 栾荣生, 王新, 孙鑫, 陈兴蜀, 周涛, 刘权辉, 吕欣, 吴先萍, 谷冬晴, 唐明霜, 崔慧杰, 单雪峰, 欧阳净, 张本, 张伟 2020 四川大学学报(医学版) 51 131
Google Scholar
Luan R S, Wang X, Sun X, Zhou T, Liu Q H, Lu X, Wu X P, Gu D Q, Tang M S, Cui H J, Shan X F, Ouyang J, Zhang B, Zhang W 2020 J. Sichuan.Univ. 51 131
Google Scholar
[9] 周涛, 刘权辉, 杨紫陌, 廖敬仪, 杨可心, 白薇, 吕欣, 张伟 2020 中国循证医学杂志 20 359
Google Scholar
Zhou T, Liu Q, Yang Z, Liao J, Yang K, Bai W, Lu X, Zhang W 2020 J. Evid.-Based Dent. Pract. Med. China 20 359
Google Scholar
[10] 谭索怡, 曹自强, 秦烁, 陈洒然, 赛斌, 郭淑慧, 刘楚楚, 蔡梦思, 周涛, 张伟, 吕欣 2020 电子科技大学学报 49 788
Google Scholar
Tan S Y, Cao Z Q, Qin S, Chen S R, Sai B, Guo S H, Liu C C, Cai M S, Zhou T, Zhang W, Lu X 2020 J. Univ. Electron. Sci. Technol. China 49 788
Google Scholar
[11] 魏永越, 卢珍珍, 杜志成, 张志杰, 赵杨, 沈思鹏, 王波, 郝元涛, 陈峰 2020 中华流行病学杂志 41 470
Google Scholar
Wei Y Z, Lu Z Z, Du Z C, Zhang Z J, Zhao Y, Shen S P, Wang B, Hao Y T, Chen F 2020 Chinese J. Epidemiology 41 470
Google Scholar
[12] Cohen J 2020 https://www.sciencemag.org/news/2020/02/scientists-are-racing-model-next-moves-coronavirus-thats-stillhard-predict [2021-1-11]
[13] Brockmann D, Helbing D 2013 Science 342 1337
Google Scholar
[14] Wu J T, Leung K, Leung G M 2020 The Lancet 395 689
Google Scholar
[15] 王聪, 严洁, 王旭, 李敏 2020 69 080701
Google Scholar
Wang C, Yan J, Wang X, Li M 2020 Acta Phys. Sin. 69 080701
Google Scholar
[16] Gross B, Zheng Z, Liu S, Chen X, Sela A, Li J, Li D, Havlin S 2020 arXiv: 2003. 08382 [Statistical Physics]
[17] 许小可, 文成, 张光耀, 孙皓宸, 刘波, 王贤文 2020 电子科技大学学报 49 324
Google Scholar
Xu X K, Wen C, Sun G Y, Sun H C, Liu B, Wang X W 2020 J. Univ. Electron. Sci. Technol. China 49 324
Google Scholar
[18] Tian H Y, Liu Y H, Li Y D, Wu C H, Chen B, Kraemer M U, Li B Y, Cai J, Xu B, Yang Q Q 2020 Science 368 638
Google Scholar
[19] Xu C H, Yu Y G, Yang Q C, Lu Z Z 2020 arXiv: 2004. 12541 [physics. soc-ph]
[20] Bengtsson L, Gaudart J, Lu X, Moore S, Wetter E, Sallah K, Rebaudet S, Piarroux R 2015 Sci. Rep. 5 8923
Google Scholar
[21] Wilson R, Erbach S E, Albert M, Power D, Tudge S, Gonzalez M, Guthrie S, Chamberlain H, Brooks C, Hughes C 2016 PLoS. Curr. 1 8
Google Scholar
[22] Lu X, Bengtsson L, Holme P 2012 Proc. Natl. Acad. Sci. U.S.A. 109 11576
Google Scholar
[23] 中华人民共和国工业和信息化部无线电管理局 (miit.gov.cn) https://www.miit.gov.cn/jgsj/wgj/gzdt/art/2020/art_87ace87acac0426a99f4213e4d578cac.html [2021-1-11]
[24] 中华人民共和国工业和信息化部无线电管理局 (miit.gov.cn) https://www.miit.gov.cn/jgsj/wgj/gggs/art/2020/art_9212747d4c794f919bd4aa03a4ca2fcf.html [2021-1-11]
[25] Holme P, Saramaki J 2012 Phys. Rep. 519 97
Google Scholar
[26] Fortunato S 2010 Phys. Rep. 486 75
Google Scholar
[27] Zipf G K 1946 Am. Sociol. Rev. 11 677
Google Scholar
[28] Blondel V D, Guillaume J L, Renaud L, Etienne L 2008 J. Stat. Mech.: Theory Exp. 10 P10008
Google Scholar
[29] Newman M E J 2004 Phys. Rev. E 70 056131
Google Scholar
[30] 新一线城市研究所 (yicai.com) https://www.maigoo.com/news/550235.html [2021-1-11]
[31] Barbosa H, Barthelemy M, Ghoshal G, James C R, Lenormand M, Louail T, Menezes R, Ramasco J J, Simini F, Tomasini M 2018 Phys. Rep. 734 1
Google Scholar
下载:
计量
- 文章访问数: 10307
- PDF下载量: 235
- 被引次数: 0
