双温度氩-氮等离子体热力学和输运性质计算

潘子晗; 陈仙辉; 王城; 夏维东

doi:10.7498/aps.70.20202040

摘要

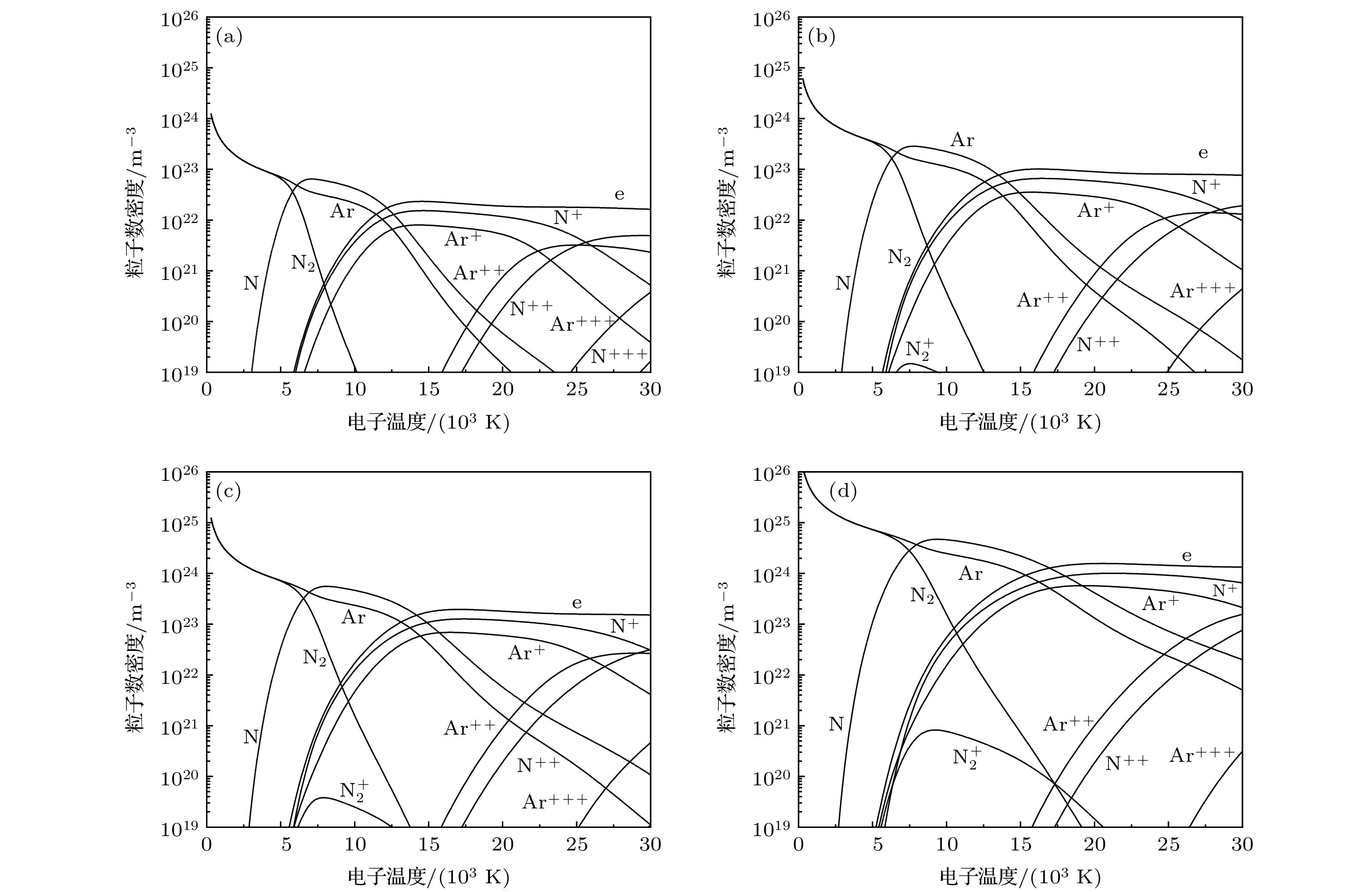
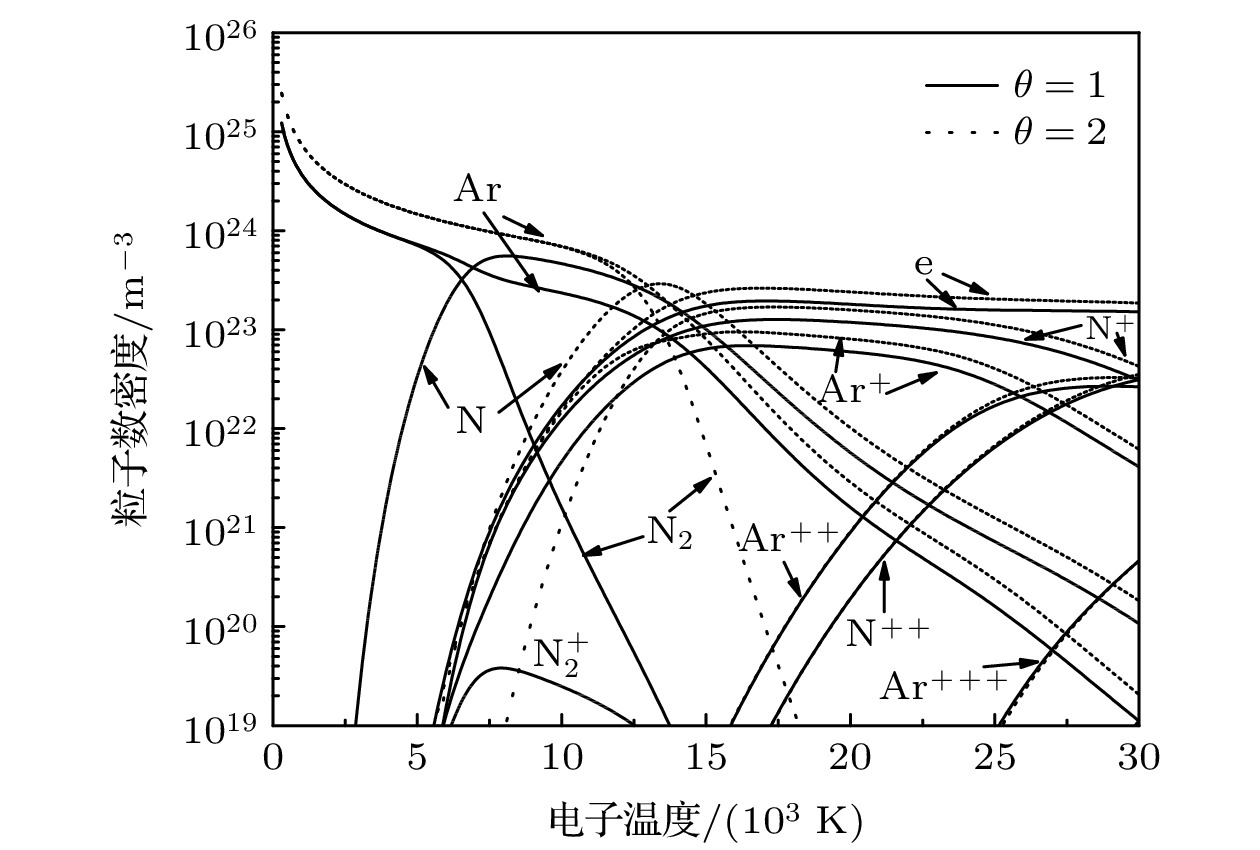
获得覆盖较宽温度和压力范围内的等离子体热力学和输运性质是开展等离子体传热和流动过程数值模拟的必要条件. 本文通过联立Saha方程、道尔顿分压定律以及电荷准中性条件求解等离子体组分; 采用理想气体动力学理论计算等离子体热力学性质; 基于Chapman-Enskog方法求解等离子体输运性质. 利用上述方法计算了压力为0.1, 1.0和10.0 atm (1 atm = 101325 Pa), 电子温度在300—30000 K范围内, 非局域热力学平衡(电子温度不等于重粒子温度)条件下氩-氮等离子体的热力学和输运性质. 结果表明压力和非平衡度会影响等离子体中各化学反应过程, 从而对氩-氮等离子体的热力学及输运性质有较大的影响. 在局域热力学平衡条件下, 计算获得的氩-氮等离子体输运性质和文献报道的数据符合良好.

关键词:

Abstract

The thermodynamic and transport properties of plasmas over a wide range of temperature and pressure are necessary to model the heat transfer and flow processes in plasma. In this study, the plasma composition is solved by simultaneous Saha equation, Dalton's partial pressure law and charge quasi-neutral equation. The thermodynamic properties of plasma computation are based on the kinetic theory for ideal gas. While the calculation of transport properties is based on the solution of Boltzmann’s equation by the Chapman-Enskog method. The thermodynamic and transport properties of argon-nitrogen plasma at pressures of 0.1, 1.0 and 10.0 atm, electron temperatures ranging from 300 to 30000 K, and non-local thermodynamic equilibrium (NLTE), where the electron temperature is not equal to the temperature of heavy particles,, are investigated by using the above method. The results show that the value of non-equilibrium parameter has a great influence on the properties of the argon-nitrogen mixture. With the increase of non-equilibrium parameter, the dissociation reaction requires a higher electron temperature, which leads the dissociation peak to shift to a higher electron temperature. The ionization and dissociation reaction will enter into the high temperature region due to the increase in pressure. This change will affect the peak position and value of the specific heat, viscosity, thermal conductivity and electrical conductivity of plasma. In addition, since the electronic translational thermal conductivity and electrical conductivity mainly depend on the electron number density, when non-equilibrium parameter and pressure increase, the electron number density will increase at high electron temperature, thus improving the electronic translational thermal conductivity and electrical conductivity. Under the condition of local thermodynamic equilibrium, the transport properties of argon-nitrogen plasma obtained by calculation are in good agreement with previously reported data.

Keywords:

argon-nitrogen plasma /
thermodynamic and transport property /
non-local thermodynamic equilibrium plasma

作者及机构信息

中国科学技术大学工程科学学院, 合肥　230022

通信作者: 陈仙辉, chenxian@mail.ustc.edu.cn ; 夏维东, xiawd@ustc.edu.cn

基金项目: 国家自然科学基金(批准号: 11675177, 11875256) 资助的课题

Authors and contacts

School of Engineering Science, University of Science and Technology of China, Hefei 230022, China

Corresponding author: Chen Xian-Hui, chenxian@mail.ustc.edu.cn ; Xia Wei-Dong, xiawd@ustc.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11675177，11875256)

文章全文 : translate this paragraph

参考文献

[1]	Fan X B, Ishigaki T 1998 Thin Solid Films. 316 174 Google Scholar
[2]	Abrar M, Farwa G U, Naseer S, Saeed A, Khan A W, Iqbal Z, Hussain S T, Zakaullah M 2013 Curr. Appl. Phys. 13 567 Google Scholar
[3]	Selvan B, Ramachandran K, Pillai B C, Subhakar D 2011 J. Therm. Spray Technol. 20 534 Google Scholar
[4]	Dias A, Bundaleski N, Tatarova E, Dias F M, Abrashev M, Cvelbar U, Teodoro O M N D, Henriques J 2016 J. Phys. D: Appl. Phys. 49 055307 Google Scholar
[5]	Yamada M, Inamoto T, Fukumoto M, Yasui T 2004 Mater. Trans. 45 3304 Google Scholar
[6]	Hirschfelder J, Curtiss C F, Bird R 1954 Molecular Theory of Gases and Liquids (New York: John Wiley and Sons) p464
[7]	Aubreton J, Elchinger M F, Hacala A, Michon U 2009 J. Phys. D: Appl. Phys. 42 095206 Google Scholar
[8]	Murphy A B 2000 Plasma Chem. Plasma Process. 20 279 Google Scholar
[9]	Murphy A B, Arundelli C J 1994 Plasma Chem. Plasma Process. 14 451 Google Scholar
[10]	Murphy A B, Tam E 2014 J. Phys. D: Appl. Phys. 47 295202 Google Scholar
[11]	Sourd B, Aubreton J, Elchinger M F, Labrot M, Michon U 2006 J. Phys. D: Appl. Phys. 39 1105 Google Scholar
[12]	Devoto R S 1967 Phys. Fluids. 10 2105 Google Scholar
[13]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2001 Phys. Rev E. 64 026409 Google Scholar
[14]	Wu Y, Chen Z X, Yang F, Cressault Y, Murphy A B, Guo A, Liu Z R, Rong M Z, Sun H 2015 J. Phys. D: Appl. Phys. 48 415205 Google Scholar
[15]	Aubreton J, Elchinger M F, Fauchais P 1998 Plasma Chem. Plasma Process. 18 1 Google Scholar
[16]	Colombo V, Ghedini E, Sanibondi P 2008 Prog. Nucl. Energy. 50 921 Google Scholar
[17]	Ghorui S, Heberlein J V R, Pfender E 2008 Plasma Chem. Plasma Process. 28 553 Google Scholar
[18]	Ghorui S, Heberlein J V R, Pfender E 2007 Plasma Chem. Plasma Process. 27 267 Google Scholar
[19]	王海兴, 孙素蓉, 陈士强 2012 61 195203 Google Scholar Wang H X, Sun S R, Chen S Q 2012 Acta Phys. Sin. 61 195203 Google Scholar
[20]	Wang H X, Chen S Q, Chen X 2012 J. Phys. D: Appl. Phys. 45 165202 Google Scholar
[21]	Aubreton A, Elchinger M F 2003 J. Phys. D: Appl. Phys. 36 1798 Google Scholar
[22]	Aubreton J, Elchinger M F, Rat V, Fauchais P 2003 J. Phys. D: Appl. Phys. 37 34
[23]	Colombo V, Ghedini E, Sanibondi P 2009 J. Phys. D: Appl. Phys. 42 055213 Google Scholar
[24]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2002 Plasma Chem. Plasma Process. 22 453 Google Scholar
[25]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2002 Plasma Chem. Plasma Process. 22 475 Google Scholar
[26]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Vacher D 2002 J. Phys. D: Appl. Phys. 35 981 Google Scholar
[27]	Godin D, Trépanier J Y 2004 Plasma Chem. Plasma Process. 24 447 Google Scholar
[28]	van de Sanden M C M, Schram P P J M, Peeters A G, van der Mullen J A M, Kroesen G M W 1989 Phys. Rev. A 40 5273 Google Scholar
[29]	Kramida A, Ralchenko Y, Reader J, NIST ASD Team https://www.nist.gov/pml/atomic-spectra-database [2020-12-1]
[30]	Chase M W, Davies C A, Downey J R, Frurip D J, McDonald R A, Syverud A N https://janaf.nist.gov/ [2020-12-1]
[31]	Aziz R A, Slaman M J 1990 J. Chem. Phys. 92 1030 Google Scholar
[32]	Capitelli M, Devoto R S 1973 Phys. Fluids. 16 1835 Google Scholar
[33]	Levin E, Partridge H, Stallcop J R 1990 J. Thermophys Heat Transfer 4 469 Google Scholar
[34]	Brunetti B, Liuti G, Luzzatti E, Pirani F, Volpi G G 1983 J. Chem. Phys. 79 273 Google Scholar
[35]	Murphy A B 1995 Plasma Chem. Plasma Process 15 279 Google Scholar
[36]	Phelps A V 1991 J. Phys. Chem. Ref. Data. 20 557 Google Scholar
[37]	Stallcop J R, Partridge H, Levin E 1991 J. Chem. Phys. 95 6429 Google Scholar
[38]	Murphy A B 1993 Phys. Rev. E 48 3594 Google Scholar
[39]	Engelhardt A G, Phelps A V, Risk C G 1964 Phys. Rev. 135 1566 Google Scholar
[40]	Neynaber R H, Marino L L, Rothe E W, Trujillo S M 1963 Phys. Rev. 129 2069 Google Scholar
[41]	Mason E A, Munn R J, Smith F J 1967 Phys. Fluids. 10 1827 Google Scholar
[42]	Devoto R S 1966 Phys. Fluids. 9 1230 Google Scholar
[43]	Chen X, Li H P 2003 Int. J. Heat Mass Transfer 46 1443 Google Scholar
[44]	Wang W Z, Rong M Z, Yan J D, Murphy A B, Spencer J W 2011 Phys. Plasmas. 18 113502 Google Scholar

施引文献

图 1 不同非平衡度下50%$ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物中各粒子数密度随电子温度的变化(1 atm)

Fig. 1. Electron temperature dependence of composition of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter (1 atm).

下载: 全尺寸图片幻灯片

图 2 LTE条件下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物中各粒子数密度随电子温度的变化　(a) 0.1 atm; (b) 0.5 atm; (c) 1.0 atm; (d) 10.0 atm

Fig. 2. Electron temperature dependence of composition of 50% argon-50% nitrogen mixtures under LTE condition: (a) 0.1 atm; (b) 0.5 atm; (c) 1.0 atm; (d) 10.0 atm.

下载: 全尺寸图片幻灯片

图 3 不同压力和非平衡度下50%$ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物热力学性质随电子温度的变化

Fig. 3. Electron temperature dependence of thermodynamic properties of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure.

下载: 全尺寸图片幻灯片

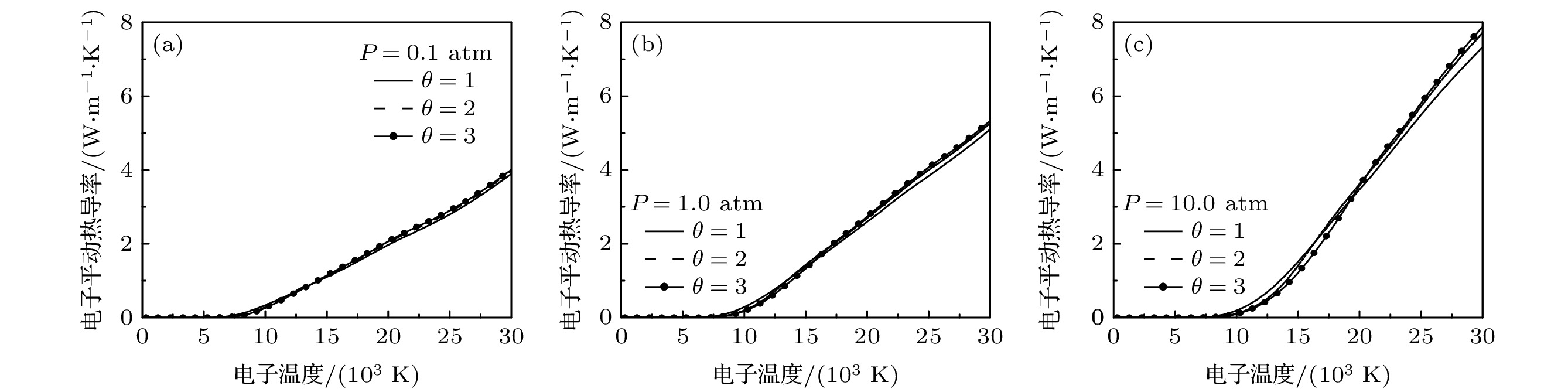
图 4 不同非平衡参数下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物反应热导率随电子温度的变化　(a)电子反应热导率; (b) 重粒子反应热导率; (c) 总反应热导率(1 atm)

Fig. 4. Electron temperature dependence of reactive thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter: (a) Reactive thermal conductivity of electrons; (b) reactive thermal conductivity of heavy particles; (c) total reactive thermal conductivity(1 atm).

下载: 全尺寸图片幻灯片

图 5 不同压力和非平衡度下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物热导率随电子温度的变化, 符号$ \times $代表Murphy和Arundelli^[9]计算结果

Fig. 5. Electron temperature dependence of total thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli^[9].

下载: 全尺寸图片幻灯片

图 6 不同压力和非平衡度下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物电子平动热导率随电子温度的变化

Fig. 6. Electron temperature dependence of electron translational thermal conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure.

下载: 全尺寸图片幻灯片

图 7 不同压力和非平衡度下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物热导率随电子温度的变化, 符号$ \times $代表Murphy和Arundelli^[9]计算结果

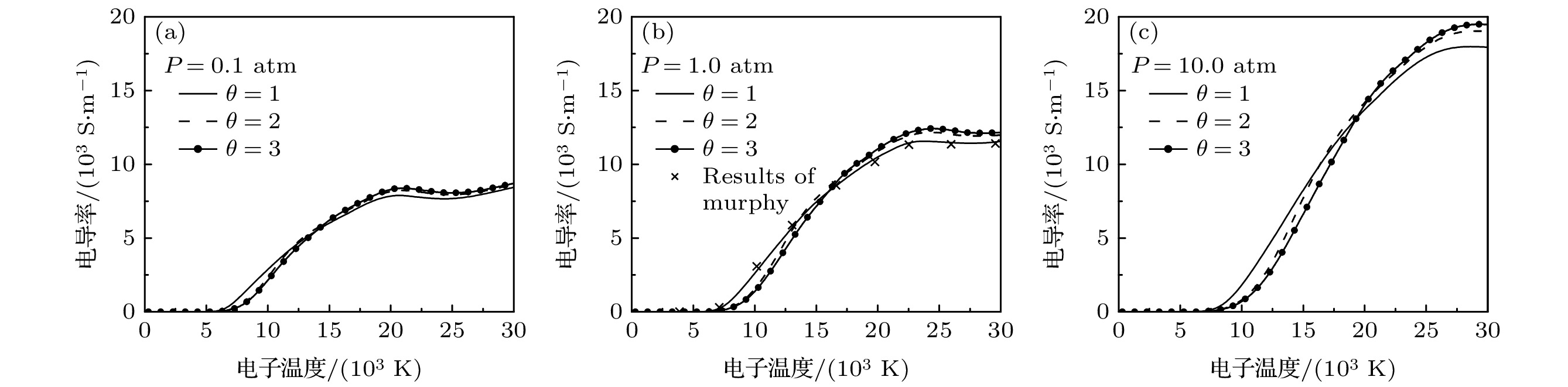
Fig. 7. Electron temperature dependence of viscosity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli^[9].

下载: 全尺寸图片幻灯片

图 8 不同压力和非平衡度下50% $ {\rm{Ar}} $和50% $ {\rm{N}}_{2} $混合物电导率随电子温度的变化, 符号$ \times $代表Murphy和Arundelli^[9]计算结果

Fig. 8. Electron temperature dependence of electrical conductivity of 50% argon-50% nitrogen mixtures for different values of non-equilibrium parameter and pressure, the symbol $ \times $ shows results of Murphy and Arundelli^[9].

下载: 全尺寸图片幻灯片

表 1 中性粒子之间相互作用

Table 1. Data source of neutral-neutral interaction

相互作用	方法	文献
Ar-Ar	HFDTCS2势	[31]
N₂-N₂	Exponential势	[32]
N₂-N	Exponential势	[32]
N-N	碰撞积分表	[33]
N₂-Ar	ESMV势	[34]
$ {\rm{Ar}} $-N	Lennard-Jones势	[34]

下载: 导出CSV

表 2 中性粒子与离子相互作用

Table 2. Data source of neutral-ion interaction.

相互作用	弹性碰撞	文献	非弹性碰撞	文献
Ar⁺-Ar	²∑_1/2u Morse势	[35]	∑ 电荷转移	[35]
	²∑_1/2g Exponential势	[35]	Π 电荷转移	[35]
	²Π_3/2g Morse势	[35]
	²Π_3/2u Exponential势	[35]
	²Π_1/2g Morse势	[35]
	²Π_1/2u Exponential势	[35]
${\rm{N}}_2^+ $-N₂	极化势		积分输运截面	[36]
${\rm{N}}_2^+ $-N	极化势
N⁺-N₂	极化势		积分输运截面	[36]
N⁺-N₂	碰撞积分表	[37]	碰撞积分表	[37]
Ar⁺-N₂	极化势
Ar⁺-N	极化势
${\rm{N}}_2^+ $-Ar	极化势
N⁺-Ar	³∑^– Morse势	[38]
	³Π Morse势	[38]
Xⁿ⁺-X, Y (n ≥ 2)	极化势

下载: 导出CSV

表 3 电子与中性粒子相互作用

Table 3. Data source of electron-neutral interaction

相互作用	方法	文献
e-N₂	积分输运截面	[39]
e-N	积分输运截面	[40]
e-Ar	积分输运截面	[26]

下载: 导出CSV

map

[1]	Fan X B, Ishigaki T 1998 Thin Solid Films. 316 174 Google Scholar
[2]	Abrar M, Farwa G U, Naseer S, Saeed A, Khan A W, Iqbal Z, Hussain S T, Zakaullah M 2013 Curr. Appl. Phys. 13 567 Google Scholar
[3]	Selvan B, Ramachandran K, Pillai B C, Subhakar D 2011 J. Therm. Spray Technol. 20 534 Google Scholar
[4]	Dias A, Bundaleski N, Tatarova E, Dias F M, Abrashev M, Cvelbar U, Teodoro O M N D, Henriques J 2016 J. Phys. D: Appl. Phys. 49 055307 Google Scholar
[5]	Yamada M, Inamoto T, Fukumoto M, Yasui T 2004 Mater. Trans. 45 3304 Google Scholar
[6]	Hirschfelder J, Curtiss C F, Bird R 1954 Molecular Theory of Gases and Liquids (New York: John Wiley and Sons) p464
[7]	Aubreton J, Elchinger M F, Hacala A, Michon U 2009 J. Phys. D: Appl. Phys. 42 095206 Google Scholar
[8]	Murphy A B 2000 Plasma Chem. Plasma Process. 20 279 Google Scholar
[9]	Murphy A B, Arundelli C J 1994 Plasma Chem. Plasma Process. 14 451 Google Scholar
[10]	Murphy A B, Tam E 2014 J. Phys. D: Appl. Phys. 47 295202 Google Scholar
[11]	Sourd B, Aubreton J, Elchinger M F, Labrot M, Michon U 2006 J. Phys. D: Appl. Phys. 39 1105 Google Scholar
[12]	Devoto R S 1967 Phys. Fluids. 10 2105 Google Scholar
[13]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2001 Phys. Rev E. 64 026409 Google Scholar
[14]	Wu Y, Chen Z X, Yang F, Cressault Y, Murphy A B, Guo A, Liu Z R, Rong M Z, Sun H 2015 J. Phys. D: Appl. Phys. 48 415205 Google Scholar
[15]	Aubreton J, Elchinger M F, Fauchais P 1998 Plasma Chem. Plasma Process. 18 1 Google Scholar
[16]	Colombo V, Ghedini E, Sanibondi P 2008 Prog. Nucl. Energy. 50 921 Google Scholar
[17]	Ghorui S, Heberlein J V R, Pfender E 2008 Plasma Chem. Plasma Process. 28 553 Google Scholar
[18]	Ghorui S, Heberlein J V R, Pfender E 2007 Plasma Chem. Plasma Process. 27 267 Google Scholar
[19]	王海兴, 孙素蓉, 陈士强 2012 61 195203 Google Scholar Wang H X, Sun S R, Chen S Q 2012 Acta Phys. Sin. 61 195203 Google Scholar
[20]	Wang H X, Chen S Q, Chen X 2012 J. Phys. D: Appl. Phys. 45 165202 Google Scholar
[21]	Aubreton A, Elchinger M F 2003 J. Phys. D: Appl. Phys. 36 1798 Google Scholar
[22]	Aubreton J, Elchinger M F, Rat V, Fauchais P 2003 J. Phys. D: Appl. Phys. 37 34
[23]	Colombo V, Ghedini E, Sanibondi P 2009 J. Phys. D: Appl. Phys. 42 055213 Google Scholar
[24]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2002 Plasma Chem. Plasma Process. 22 453 Google Scholar
[25]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Lefort A 2002 Plasma Chem. Plasma Process. 22 475 Google Scholar
[26]	Rat V, André P, Aubreton J, Elchinger M F, Fauchais P, Vacher D 2002 J. Phys. D: Appl. Phys. 35 981 Google Scholar
[27]	Godin D, Trépanier J Y 2004 Plasma Chem. Plasma Process. 24 447 Google Scholar
[28]	van de Sanden M C M, Schram P P J M, Peeters A G, van der Mullen J A M, Kroesen G M W 1989 Phys. Rev. A 40 5273 Google Scholar
[29]	Kramida A, Ralchenko Y, Reader J, NIST ASD Team https://www.nist.gov/pml/atomic-spectra-database [2020-12-1]
[30]	Chase M W, Davies C A, Downey J R, Frurip D J, McDonald R A, Syverud A N https://janaf.nist.gov/ [2020-12-1]
[31]	Aziz R A, Slaman M J 1990 J. Chem. Phys. 92 1030 Google Scholar
[32]	Capitelli M, Devoto R S 1973 Phys. Fluids. 16 1835 Google Scholar
[33]	Levin E, Partridge H, Stallcop J R 1990 J. Thermophys Heat Transfer 4 469 Google Scholar
[34]	Brunetti B, Liuti G, Luzzatti E, Pirani F, Volpi G G 1983 J. Chem. Phys. 79 273 Google Scholar
[35]	Murphy A B 1995 Plasma Chem. Plasma Process 15 279 Google Scholar
[36]	Phelps A V 1991 J. Phys. Chem. Ref. Data. 20 557 Google Scholar
[37]	Stallcop J R, Partridge H, Levin E 1991 J. Chem. Phys. 95 6429 Google Scholar
[38]	Murphy A B 1993 Phys. Rev. E 48 3594 Google Scholar
[39]	Engelhardt A G, Phelps A V, Risk C G 1964 Phys. Rev. 135 1566 Google Scholar
[40]	Neynaber R H, Marino L L, Rothe E W, Trujillo S M 1963 Phys. Rev. 129 2069 Google Scholar
[41]	Mason E A, Munn R J, Smith F J 1967 Phys. Fluids. 10 1827 Google Scholar
[42]	Devoto R S 1966 Phys. Fluids. 9 1230 Google Scholar
[43]	Chen X, Li H P 2003 Int. J. Heat Mass Transfer 46 1443 Google Scholar
[44]	Wang W Z, Rong M Z, Yan J D, Murphy A B, Spencer J W 2011 Phys. Plasmas. 18 113502 Google Scholar

[1]	胡敏丽, 房凡, 樊群超, 范志祥, 李会东, 付佳, 谢锋. NO⁺离子系统热力学性质的理论研究. , 2023, 72(16): 165101. doi: 10.7498/aps.72.20230541
[2]	朱诚, 陈仙辉, 王城, 宋明, 夏维东. 氩-碳-硅等离子体热力学性质和输运系数计算. , 2023, 72(12): 125202. doi: 10.7498/aps.72.20222390
[3]	王子, 任捷. 周期驱动系统的非平衡热输运与热力学几何. , 2021, 70(23): 230503. doi: 10.7498/aps.70.20211723
[4]	罗菊, 冯国英, 韩敬华, 沈雄, 张丽君, 丁坤艳. 激光等离子体去除微纳颗粒的热力学研究. , 2020, 69(8): 084201. doi: 10.7498/aps.69.20191933
[5]	汤文辉, 徐彬彬, 冉宪文, 徐志宏. 高温等离子体的状态方程及其热力学性质. , 2017, 66(3): 030505. doi: 10.7498/aps.66.030505
[6]	王伟宗, 吴翊, 荣命哲, 杨飞. 局域热力学平衡态空气电弧等离子体输运参数计算研究. , 2012, 61(10): 105201. doi: 10.7498/aps.61.105201
[7]	李晓凤, 刘中利, 彭卫民, 赵阿可. 高压下CaPo弹性性质和热力学性质的第一性原理研究. , 2011, 60(7): 076501. doi: 10.7498/aps.60.076501
[8]	张丽春, 李怀繁, 赵仁. Schwarzchild-de Sitter 黑洞的热力学性质. , 2010, 59(12): 8994-8998. doi: 10.7498/aps.59.8994
[9]	唐先柱, 彭增辉, 刘永刚, 鲁兴海, 宣丽. 相变前的热力学平衡态对铁电液晶排列的影响. , 2010, 59(9): 6261-6265. doi: 10.7498/aps.59.6261
[10]	陈怡, 申江. NaZn13型Fe基化合物的结构和热力学性质研究. , 2009, 58(13): 141-S145. doi: 10.7498/aps.58.141
[11]	宋海峰, 刘海风. 金属铍热力学性质的理论研究. , 2007, 56(5): 2833-2837. doi: 10.7498/aps.56.2833
[12]	王红艳, 段文山. 对含有非热力学平衡离子的尘埃等离子体中孤波特性的理论研究. , 2007, 56(7): 3977-3983. doi: 10.7498/aps.56.3977
[13]	沈惠川. 分析热力学的应用：平衡态热力学中温度的相对论变换. , 2005, 54(6): 2482-2488. doi: 10.7498/aps.54.2482
[14]	朱志艳, 朱正和, 高　涛, 蒋　刚. 金等离子体中Au48+—Au52+平衡分布的统计热力学研究　. , 2004, 53(10): 3330-3335. doi: 10.7498/aps.53.3330
[15]	梁芳营. 高温超导体的热力学性质的研究. , 2002, 51(4): 898-901. doi: 10.7498/aps.51.898
[16]	周维亚, 张玉芬, 王刚, 董成, 吴非, 钱生法, 丁雪舟, 毛建民, 李楠, 付春生, 解思深. C_(60)单晶的低温热力学性质. , 1995, 44(2): 238-243. doi: 10.7498/aps.44.238
[17]	杜宜瑾, 陈立溁, 严祖同. 二维系统的热力学性质. , 1982, 31(7): 939-944. doi: 10.7498/aps.31.939
[18]	孙鑫, 叶红娟, 黄静宜. 铁磁体的热力学性质. , 1964, 20(9): 940-946. doi: 10.7498/aps.20.940
[19]	乔登江. 等离子体的热力学研究. , 1960, 16(7): 369-378. doi: 10.7498/aps.16.369
[20]	程开甲. 内耗的热力学研究(Ⅰ). , 1955, 11(2): 163-178. doi: 10.7498/aps.11.163

计量

文章访问数: 6756
PDF下载量: 167
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板