-
电子输运系数是确保低温等离子体建模准确性的关键因素, 通过模拟电子的输运过程可对其数值求解. 在模拟电子输运时, 电子和中性粒子碰撞后的散射和能量分配方式有多种处理方法. 为了研究不同处理方法对电子输运系数的影响, 本文基于蒙特卡罗碰撞方法, 建立了电子输运系数的计算模型, 模拟约化电场10—1000 Td (1 Td = 10–21 V·m2)氢原子气中的电子输运过程. 计算结果表明, 各向同性假设对电子输运系数的影响随电场强度增加而增加, 但即使对于较低的约化电场(10 Td), 各向异性散射假设下电子的平均能量、通量迁移率和通量扩散系数也分别比各向同性假设下的值高38.34%, 17.38%和119.18%. 不同的能量分配方式对中高电场强度下(> 200 Td)的电子输运系数影响较为显著. 在高电场时, 均分法计算得出的电子平均能量、通量迁移率和通量扩散系数均小于零分法对应的值, 汤森电离系数则相反. Opal法得出的电子输运系数介于均分法和零分法之间. 此外, 考虑各向异性散射时, 不同能量分配方式对输运系数的影响高于各向同性. 本研究表明, 在计算电子输运系数时需要考虑各向异性的电子散射, 高电场条件下尤其要注意能量分配方式的选择.The veracity of a low temperature plasma model is limited by the accuracy of the electron transport coefficient, which can be solved by simulating the electron transport process. When simulating the transport properties of electrons, there are a variety of approaches to dealing with the scattering of electrons and energy partition between the primary-electrons and secondary-electrons after electron-neutral particles’ collision. In this paper used is a model based on the Monte Carlo collision method to investigate the influence of scattering method and energy partition method on the electron transport coefficient. The electron energy distribution function, electron mean energy, flux mobility and diffusion coefficients, as well as the Townsend ionization coefficients are calculated in the hydrogen atom gas under a reduced electric field from 10 to 1000 Td. The calculation results show that the influence of the isotropic scattering assumption on the electron transport coefficients increases with reduced electric field increasing. However, even under a relatively low reduced electric field (10 Td), the calculated mean energy, flux mobility, and flux diffusion coefficient of electrons under the assumption of anisotropic scattering are 39.68%, 17.38% and 119.18% higher than those under the assumption of the isotropic scattering. The different energy partition methods have a significant influence on the electron transport coefficient under a medium-to-high reduced electric field (> 200 Td). Under a high electric field, the mean energy, flux mobility and flux diffusion coefficient calculated by the equal-partition method (the primary and secondary electrons equally share the available energy) are all less than the values from the zero-partition method (the energy of secondary-electrons is assigned to zero). While the change of Townsend ionization coefficient with reduced electric fields shows a different trend. The electron transport coefficient obtained by the Opal method lies between the values from the equal-partition method and the zero-partition method. In addition, considering the anisotropic scattering, the influence of energy partition method on the transport coefficient is higher than that under the assumption of isotropic scattering. This study shows the necessity of considering the anisotropic electron scattering for calculating the electron transport coefficient, and special attention should be paid to the choice of energy partition method under a high reduced electric field.
[1] Samukawa S, Hori M, Rauf S, Tachibana K, Bruggeman P, Kroesen G, Whitehead J C, Murphy A B, Gutsol A F, Starikovskaia S 2012 J. Phys. D: Appl. Phys. 45 253001
Google Scholar
[2] Petrović Z L, Dujko S, Marić D, Malović G, Nikitović Ž, Šašić O, Jovanović J, Stojanović V, Radmilović-Rađenović M 2009 J. Phys. D: Appl. Phys. 42 194002
Google Scholar
[3] Konovalov D A, Cocks D G, White R D 2017 Eur. Phy. J. D 71 258
Google Scholar
[4] Stephens J 2018 J. Phys. D: Appl. Phys. 51 125203
Google Scholar
[5] Dutton J 1975 J. Phys. Chem. Ref. Data 4 577
Google Scholar
[6] Hagelaar G, Pitchford L 2005 Plasma Sources Sci. Technol. 14 722
Google Scholar
[7] Rabie M, Franck C M 2016 Comput. Phys. Commun. 203 268
Google Scholar
[8] Gallagher J, Beaty E, Dutton J, Pitchford L 1983 J. Phys. Chem. Ref. Data 12 109
Google Scholar
[9] Banković A, Dujko S, White R D, Buckman S, Petrović Z L 2012 Eur. Phy. J. D 66 174
Google Scholar
[10] Kortshagen U, Parker G, Lawler J 1996 Phys. Rev. E 54 6746
Google Scholar
[11] Yousfi M, Hennad A, Alkaa A 1994 Phys. Rev. E 49 3264
Google Scholar
[12] Longo S 2000 Plasma Sources Sci. Technol. 9 468
Google Scholar
[13] Dujko S, White R D, Petrović Z L 2008 J. Phys. D: Appl. Phys. 41 245205
Google Scholar
[14] 孙安邦, 李晗蔚, 许鹏, 张冠军 2017 66 195101
Google Scholar
Sun A B, Li H W, Xu P, Zhang G J 2017 Acta Phys. Sin. 66 195101
Google Scholar
[15] Phelps A, Pitchford L 1985 Phys. Rev. A 31 2932
Google Scholar
[16] Janssen J, Pitchford L, Hagelaar G, van Dijk 2016 Plasma Sources Sci. Technol. 25 055026
Google Scholar
[17] Yang W, Meng X, Zhou Q, Dong Z 2019 AIP Adv. 9 035041
Google Scholar
[18] Opal C, Peterson W, Beaty E 1971 J. Chem. Phys. 55 4100
Google Scholar
[19] Vahedi V, Surendra M 1995 Comput. Phys. Commun. 87 179
Google Scholar
[20] Yoshida S, Phelps A, Pitchford L 1983 Phys. Rev. A 27 2858
Google Scholar
[21] Tzeng Y, Kunhardt E 1986 Phys. Rev. A 34 2148
Google Scholar
[22] 周前红, 董志伟, 简贵胄, 周海京 2015 64 205206
Google Scholar
Zhou Q H, Dong Z W, Jian G Z, Zhou H J 2015 Acta Phys. Sin. 64 205206
Google Scholar
[23] Surendra M, Graves D, Jellum G 1990 Phys. Rev. A 41 1112
Google Scholar
[24] Jiang P, Economou D J 1993 J. Appl. Phys. 73 8151
Google Scholar
[25] Nolan A, Brennan M J, Ness K, Wedding A 1997 J. Phys. D: Appl. Phys. 30 2865
Google Scholar
[26] Dalgarno A, Yan M, Liu W 1999 Astrophys. J. Suppl. Ser. 125 237
Google Scholar
[27] Janev R K, Smith J J http://www-amdis.iaea.org [2021-2-7]
[28] Hagelaar G http://www.bolsig.laplace.univ-tlse.fr/ [2021-2-7]
[29] Belenguer P, Pitchford L 1999 J. Appl. Phys. 86 4780
Google Scholar
-
图 1 电子与氢原子弹性和电离碰撞的截面数据
Fig. 1. Elastic and ionization cross sections between electron and hydrogen atoms.
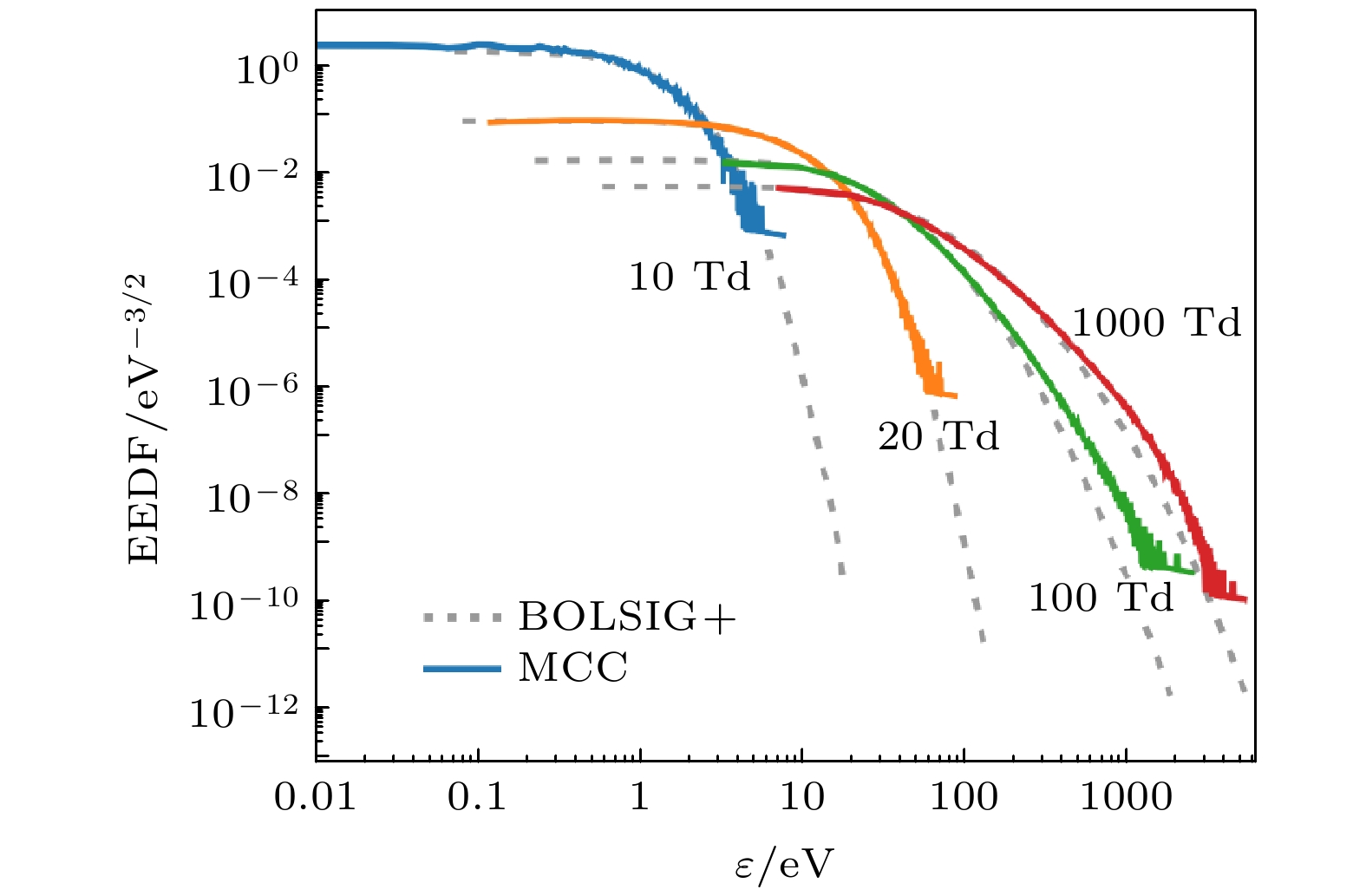
图 2 MCC模型和BOLSIG+软件在约化电场为10, 20, 100和1000 Td计算出的EEDF对比(电子散射各向同性, 能量均分). 实线和虚线分别代表MCC模型和BOLSIG+软件的计算结果
Fig. 2. Comparison of EEDF calculated by MCC model and BOLSIG+ software with isotropic scattering and equally energy partition under the reduced fields of 10, 20, 100 and 1000 Td. Dashed lines from MCC, and solid lines from BOLSIG+ software.
图 3 MCC模型和BOLSIG+软件计算出的电子输运系数对比(电子散射各向同性, 均分法) (a)电子平均能量; (b)电离系数; (c)横向扩散系数; (d)迁移系数. 橙色实线和绿色虚线分别为使用BOLSIG+软件和MCC法计算的结果
Fig. 3. Comparison of electron transport coefficients calculated by MCC model and BOLSIG+ software with isotropic scattering and equally energy partition: (a) Mean energy; (b)Townsend ionization coefficients; (c) flux diffusion coefficients; (d) flux mobility. Dashed-orange lines from MCC, and solid-green lines from BOLSIG+ software.
图 4 不同散射条件下电子能量分布函数和沿电场方向的速度概率函数在约化电场为10, 20和100 Td时的值 (a)电子能量分布函数; (b)沿电场方向电子速度概率函数. 图中实线为各向异性散射, 虚线为各向同性散射
Fig. 4. (a) Electron energy distribution function and (b) the probability function of velocity along the electric field direction with different scattering for reduced fields 10, 20 and 100 Td. Dashed lines from isotropic scattering, and solid lines from anisotropic scattering.
图 5 电子散射各向同性和各向异性条件下电子输运系数和平均能量的计算结果对比 (a)电子平均能量; (b)电离系数; (c)横向扩散系数; (d)迁移系数. 图中方块代表各向异性, 圆点代表各向同性
Fig. 5. Comparison of electron transport coefficients calculated assuming isotropic and anisotropic scattering: (a) Mean energy; (b) townsend ionization coefficients; (c) flux diffusion coefficients; (d) flux mobility. The orange rectangle and green circle represent the results assuming the anisotropic and isotropic scattering, respectively.
图 6 不同能量分配下电子的速度相图 (a)均分法; (b)Opal法; (c)零分法. 图中圆点代表散射电子, 三角形代表二次电子
Fig. 6. The velocity phase diagram of electrons using different energy partition methods: (a) Equal-division method; (b) opal method; (c) zero-division method. Blue dots represent the primary electrons, and orange triangles represent secondary electrons.
图 7 不同散射和能量分配方式下电子输运系数和平均能量的计算结果对比 (a)电子平均能量; (b)电离系数; (c)横向扩散系数; (d)迁移系数. 图中方块、圆点和三角依次代表均分、Opal和零分法. 实线和虚线分别代表各向异性和各向同性散射
Fig. 7. Comparison of electron transport coefficients calculated with different scattering and energy partition methods: (a) Mean energy; (b) Townsend ionization coefficients; (c) flux diffusion coefficients; (d) flux mobility. The rectangle, circle, and triangles represent the calculation results using the equal-division, Opal and zero-division method, respectively. Dashed/solid lines are the results assuming the isotropic/anisotropic scattering.
表 1 约化电场为1000 Td时, 均分法和零分法在不同电子散射下电子输运系数的差异
Table 1. Difference between the electron transport coefficients using the equal and zero-division method, assuming anisotropic and isotropic scattering, respectively.
电子散射 $\left\langle\varepsilon \right\rangle$ $ \alpha $ $ {\mu }_{\rm{f}} $ $ {D}_{\rm{f}} $ 各向同性 20.92% 28.67% 0.76% 30.50% 各项异性 29.22% 42.60% 20.75% 45.06% 注: 计算方法为$({A_{{\rm{equal}}}} - {A_{{\rm{zero}}}})/{A_{{\rm{zero}}}}$, A代表电子平均能量和输运系数的值. 
下载: 导出CSV
-
[1] Samukawa S, Hori M, Rauf S, Tachibana K, Bruggeman P, Kroesen G, Whitehead J C, Murphy A B, Gutsol A F, Starikovskaia S 2012 J. Phys. D: Appl. Phys. 45 253001
Google Scholar
[2] Petrović Z L, Dujko S, Marić D, Malović G, Nikitović Ž, Šašić O, Jovanović J, Stojanović V, Radmilović-Rađenović M 2009 J. Phys. D: Appl. Phys. 42 194002
Google Scholar
[3] Konovalov D A, Cocks D G, White R D 2017 Eur. Phy. J. D 71 258
Google Scholar
[4] Stephens J 2018 J. Phys. D: Appl. Phys. 51 125203
Google Scholar
[5] Dutton J 1975 J. Phys. Chem. Ref. Data 4 577
Google Scholar
[6] Hagelaar G, Pitchford L 2005 Plasma Sources Sci. Technol. 14 722
Google Scholar
[7] Rabie M, Franck C M 2016 Comput. Phys. Commun. 203 268
Google Scholar
[8] Gallagher J, Beaty E, Dutton J, Pitchford L 1983 J. Phys. Chem. Ref. Data 12 109
Google Scholar
[9] Banković A, Dujko S, White R D, Buckman S, Petrović Z L 2012 Eur. Phy. J. D 66 174
Google Scholar
[10] Kortshagen U, Parker G, Lawler J 1996 Phys. Rev. E 54 6746
Google Scholar
[11] Yousfi M, Hennad A, Alkaa A 1994 Phys. Rev. E 49 3264
Google Scholar
[12] Longo S 2000 Plasma Sources Sci. Technol. 9 468
Google Scholar
[13] Dujko S, White R D, Petrović Z L 2008 J. Phys. D: Appl. Phys. 41 245205
Google Scholar
[14] 孙安邦, 李晗蔚, 许鹏, 张冠军 2017 66 195101
Google Scholar
Sun A B, Li H W, Xu P, Zhang G J 2017 Acta Phys. Sin. 66 195101
Google Scholar
[15] Phelps A, Pitchford L 1985 Phys. Rev. A 31 2932
Google Scholar
[16] Janssen J, Pitchford L, Hagelaar G, van Dijk 2016 Plasma Sources Sci. Technol. 25 055026
Google Scholar
[17] Yang W, Meng X, Zhou Q, Dong Z 2019 AIP Adv. 9 035041
Google Scholar
[18] Opal C, Peterson W, Beaty E 1971 J. Chem. Phys. 55 4100
Google Scholar
[19] Vahedi V, Surendra M 1995 Comput. Phys. Commun. 87 179
Google Scholar
[20] Yoshida S, Phelps A, Pitchford L 1983 Phys. Rev. A 27 2858
Google Scholar
[21] Tzeng Y, Kunhardt E 1986 Phys. Rev. A 34 2148
Google Scholar
[22] 周前红, 董志伟, 简贵胄, 周海京 2015 64 205206
Google Scholar
Zhou Q H, Dong Z W, Jian G Z, Zhou H J 2015 Acta Phys. Sin. 64 205206
Google Scholar
[23] Surendra M, Graves D, Jellum G 1990 Phys. Rev. A 41 1112
Google Scholar
[24] Jiang P, Economou D J 1993 J. Appl. Phys. 73 8151
Google Scholar
[25] Nolan A, Brennan M J, Ness K, Wedding A 1997 J. Phys. D: Appl. Phys. 30 2865
Google Scholar
[26] Dalgarno A, Yan M, Liu W 1999 Astrophys. J. Suppl. Ser. 125 237
Google Scholar
[27] Janev R K, Smith J J http://www-amdis.iaea.org [2021-2-7]
[28] Hagelaar G http://www.bolsig.laplace.univ-tlse.fr/ [2021-2-7]
[29] Belenguer P, Pitchford L 1999 J. Appl. Phys. 86 4780
Google Scholar
下载:
计量
- 文章访问数: 5577
- PDF下载量: 105
- 被引次数: 0
