-
作为凝聚态物理中一类新奇准粒子态, Majorana零能模(Majorana zero mode)由于可用来实现拓扑量子计算而成为当前的研究热点. 理论预言, Majorana零能模可作为特殊的束缚态出现在一些拓扑超导体的磁通涡旋中. 但实际超导体磁通中还可能存在其他低能束缚态或杂质态, 这给Majorana零能模的辨别和具体应用带来了困难. 目前实验上寻找合适的拓扑超导体系、分辨出清晰的Majorana零能模仍然是十分迫切的. 本文主要介绍最近利用高能量分辨的扫描隧道显微镜, 对电子掺杂铁硒类超导体(Li, Fe)OHFeSe和单层FeSe/SrTiO3磁通态进行的研究. 实验上在前者的自由磁通中观测到清晰的零能模, 并进一步测量到Majorana零能模的重要特征—量子化电导. 而在后者磁通中只发现常规Caroli-de Gennes-Matricon (CdGM)束缚态, 反映出s波对称性的特征. 这系列实验既为Majorana零能模物性的进一步研究提供了合适平台, 也为澄清铁基超导体中拓扑超导电性的来源提供了线索.
-
关键词:
- 磁通涡旋 /
- 束缚态 /
- Majorana零能模 /
- 拓扑超导体 /
- 量子化电导
As a novel quantum state in condensed matter physics, Majorana zero mode has become a popular research topic at present because of its potential value in topological quantum computing. Theory predicts that Majorana zero mode appears in the vortex core of the topological superconductor as a unique bound state. However, due to various factors such as the existence of conventional low energy bound states or impurity states, it is difficult to identify the Majorana zero mode and to put it into the specific applications. Nowadays, it is still urgent to find a suitable topological superconducting system and identify the clean Majorana zero mode in experiment. In this paper, we study the vortex states of electron-doped iron-selenium-based superconductors (Li, Fe)OHFeSe and single-layer FeSe/SrTiO3 with extremely high energy resolution STM. There exists a robust and clean Majorana zero mode in the free vortex core of (Li, Fe)OHFeSe, which has the quantized conductance. As for single-layer FeSe/SrTiO3 film, it has only conventional Caroli-de Gennes-Matricon (CdGM) bound states without zero energy mode. These experimental results provide a suitable platform for further studying the physical properties of Majorana zero mode, and also shed light on the source of topological superconductivity in iron-based superconductors.-
Keywords:
- magnetic vortex /
- vortex bound states /
- Majorana zero mode /
- topological superconductor /
- quantized conductance
[1] Caroli C, de Gennes P G, Matricon J 1964 Phys. Lett. 9 307
[2] Volovik G E 1999 JETP Lett. 70 609
[3] Read N, Green D 2000 Phys. Rev. B 61 10267
[4] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
[5] Alicea J 2012 Rep. Prog. Phys. 75 076501
[6] Leijnse M, Flensberg K 2012 Semicond. Sci. Technol. 27 124003
[7] Beenakker C W J 2013 Annu. Rev. Condens. Matter Phys. 4 113
[8] Sato M, Ando Y 2017 Rep. Prog. Phys. 80 076501
[9] Kitaev A 2003 Ann. Phys. 303 2
[10] Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083
[11] Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407
[12] Wang M X, Liu C, Xu J P, Yang F, Miao L, Yao M Y, Gao C L, Shen C, Ma X, Chen X, Xu Z A, Liu Y, Zhang S C, Qian D, Jia J F, Xue Q K 2012 Science 336 52
 Google Scholar
Google Scholar
[13] Xu J P, Liu C, Wang M X, Ge J, Liu Z L, Yang X, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001
[14] Xu J P, Wang M X, Liu Z L, Ge J F, Yang X, Liu C, Xu Z A, Guan D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001
[15] Sun H H, Zhang K W, Hu L H, Li C, Wang G Y, Ma H Y, Xu Z A, Gao C L, Guan D D, Li Y Y, Liu C, Qian D, Zhou Y, Fu L, Li S C, Zhang F C, Jia J F 2016 Phys. Rev. Lett. 116 257003
[16] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers EPAM, Kouwenhoven L P 2012 Science 336 1003
 Google Scholar
Google Scholar
[17] Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, Shtrikman H 2012 Nat. Phys. 8 887
[18] Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602
 Google Scholar
Google Scholar
[19] Jeon S, Xie Y, Li J, Wang Z, Bernevig B A, Yazdani A 2017 Science 358 772
 Google Scholar
Google Scholar
[20] Zhang H, Liu C X, Gazibegovic S, Xu D, Logan J A, Wang G, van Loo N, Bommer J D S, de Moor M W A, Car D, Op Het Veld R L M, van Veldhoven P J, Koelling S, Verheijen M A, Pendharkar M, Pennachio D J, Shojaei B, Lee J S, Palmstrom C J, Bakkers E P A M, Sarma S D, Kouwenhoven L P 2018 Nature 556 74
[21] Suderow H, Guillamón I, Rodrigo J G, Vieira S 2014 Supercond. Sci. Technol. 27 063001
[22] Hess H F, Robinson R B, Dynes R C, Valles J M, Jr Waszczak J V 1989 Phys. Rev. Lett. 62 214
[23] Hess H F, Robinson R B, Waszczak J V 1990 Phys. Rev. Lett. 64 2711
[24] Hayashi N, Isoshima T, Ichioka M, Machida K 1998 Phys. Rev. Lett. 80 2921
[25] Song C L, Wang Y L, Cheng P, Jiang Y P, Li Wei, Zhang T, Li Z, He K, Wang L L, Jia J F, Hung H H, Wu C J, Ma X C, Chen X, Xue Q K 2011 Science 332 1410
 Google Scholar
Google Scholar
[26] Hanaguri T, Kitagawa K, Matsubayashi K, Mazaki Y, Uwatoko Y, Takagi H 2012 Phys. Rev. B 85 214505
[27] Zhou B B, Misra S, da Silva Neto E H, Aynajian P, Baumbach R E, Thompson J D, Bauer E D Yazdani A 2013 Nat. Phys. 9 474
[28] Hao N, Hu J 2014 Phys. Rev. X 4 031053
[29] Wang Z, Zhang P, Xu G, Zeng L K, Miao H, Xu X, Qian T, Weng H, Richard P, Fedorov A V, Ding H, Dai X, Fang Z 2015 Phys. Rev. B 92 115119
[30] Xu G, Lian B, Tang P, Qi X L, Zhang S C 2016 Phys. Rev. Lett. 117 047001
[31] 郝宁, 胡江平 2018 67 207101
 Google Scholar
Google Scholar
Hao N, Hu J P 2018 Acta Phys. Sin. 67 207101
 Google Scholar
Google Scholar
[32] Chen M Y, Chen X, Yang H, Du Z, Zhu X, Wang E, Wen H H 2018 Nat. Commun. 9 970
[33] Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333
 Google Scholar
Google Scholar
[34] Machida T, Sun Y, Pyon S, Takeda S, Kohsaka Y, Hanaguri T, Sasagawa T, Tamegai T 2019 Nat. Mater. 18 811
[35] Kong L Y, Zhu S Y, Papaj M, Chen H, Cao L, Isobe H, Xing Y Q, Liu W Y, Wang D F, Fan P, Sun Y J, Du S X, Schneeloch J, Zhong R D, Gu G D, Fu L, Gao H J, Ding H 2019 Nat. Phys. 15 1181
[36] Zhang P, Yaji K, Hashimoto T, Ota Y, Kondo T, Okazaki K, Wang Z, Wen J, Gu G D, Ding H, Shin S 2018 Science 360 182
 Google Scholar
Google Scholar
[37] Chiu C K, Machida T, Huang Y, Hanaguri T, Zhang F C 2020 Sci. Adv. 6 eaay0443
 Google Scholar
Google Scholar
[38] Balatsky A V 2006 Rev. Mod. Phys. 78 373
[39] Lee E J H, Jiang X, Aguado R, Katsaros G, Lieber C M, de Franceschi S 2012 Phys. Rev. Lett. 109 186802
[40] Levy N, Zhang T, Ha J, Sharifi F, Talin A A, Kuk Y, Stroscio J A 2013 Phys. Rev. Lett. 110 117001
[41] Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001
[42] Setiawan F, Liu C X, Sau J D, Sarma S D 2017 Phys. Rev. B 96 184520
[43] He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001
[44] Kawakami T, Hu X 2015 Phys. Rev. Lett. 115 177001
[45] Hu L H, Li C, Xu D H, Zhou Y, Zhang F C 2016 Phys. Rev. B 94 224501
[46] Liu Q, Chen C, Zhang T, Peng R, Yan Y J, Wen C H P, Lou X, Huang Y L, Tian J P, Dong X L, Wang G W, Bao W C, Wang Q H, Yin Z P, Zhao Z X, Feng D L 2018 Phys. Rev. X 8 041056
[47] Chen C, Liu Q, Zhang T Z, Li D, Shen P P, Dong X L, Zhao Z X, Zhang T, Feng D L 2019 Chin. Phys. Lett. 36 057403
[48] Chen C, Liu Q, Bao W C, Yan Y J, Wang Q H, Zhang T, Feng D L 2020 Phys. Rev. Lett. 124 097001
[49] Dong X, Jin K, Yuan D, Zhou H, Yuan J, Huang Y, Hua W, Sun J, Zheng P, Hu W, Mao Y, Ma M, Zhang G, Zhou F, Zhao Z 2015 Phys. Rev. B 92 064515
[50] Lu X F, Wang N Z, Wu H, Wu Y P, Zhao D, Zeng X Z, Luo X G, Wu T, Bao W, Zhang G H, Huang F Q, Huang Q Z, Chen X H 2015 Nat. Mater. 14 325
[51] Niu X H, Peng R, Xu H C, Yan Y J, Jiang J, Xu D F, Yu T L, Song Q, Huang Z C, Wang Y X, Xie B P, Lu X F, Wang N Z, Chen X H, Sun Z, Feng D L 2015 Phys. Rev. B 92 060504(R)
[52] L. Zhao, Liang A J, Yuan D N, Hu Y, Liu D F, Huang J W, He S L, Shen B, Xu Y, Liu X, Yu L, Liu G D, Zhou H X, Huang Y L, Dong X L, Zhou F, Liu K, Lu Z Y, Zhao Z X, Chen C T, Xu Z Y, Zhou X J 2016 Nat. Commun. 7 10608
[53] Georges A, Kotliar G, Krauth W, Rozenberg M J 1996 Rev. Mod. Phys. 68 13
[54] Kotliar G, Savrasov S Y, Haule K, Oudovenko V S, Parcollet O, Marianetti C A 2006 Rev. Mod. Phys. 78 865
[55] Huang Y L, Feng Z P, Ni S L, Li J, Hu W, Liu S B, Mao Y Y, Zhou H X, Zhou F, Jin K, Wang H B, Yuan J, Dong X L, Zhao Z X 2017 Chin. Phys. Lett. 34 077404
[56] Huang Y L, Feng Z P, Yuan J, Hu W, Li J, Ni S L, Liu S B, Mao Y Y, Zhou H X, Wang H B, Zhou F, Zhang G M, Jin K, Dong X L, Zhao Z X 2017 arXiv: 1711.02920
[57] Yi M, Liu Z K, Zhang Y, Yu R, Zhu J X, Lee J J, Moore R G, Schmitt F T, Li W, Riggs S C, Chu J H, Lv B, Hu J, Hashimoto M, Mo S K, Hussain Z, Mao Z Q, Chu C W, Fisher I R, Si Q, Shen Z X, Lu D H 2015 Nat. Commun. 6 7777
[58] Yan Y J, Zhang W H, Ren M Q, Liu X, Lu X F, Wang N Z, Niu X H, Fan Q, Miao J, Tao R, Xie B P, Chen X H, Zhang T, Feng D L 2016 Phys. Rev. B 94 134502
[59] Ren M Q, Yan Y J, Niu X H, Tao R, Hu D, Peng R, Xie B P, Zhao J, Zhang T, Feng D L 2017 Sci. Adv. 3 e1603238
 Google Scholar
Google Scholar
[60] Du Z Y, Yang X, Altenfeld D, Gu Q Q, Yang H, Eremin I, Hirschfeld P J, Mazin I I, Lin H, Zhu X Y, Wen H H 2018 Nat. Phys. 14 134
[61] Kells G, Meidan D, Brouwer P W 2012 Phys. Rev. B 86 100503
[62] Liu C X, Sau J D, Stanescu T D, Sarma S D 2017 Phys. Rev. B 96 075161
[63] Zhu S Y, Kong L, Cao L, Chen H, Papaj M, Du S, Xing Y, Liu W, Wang D, Shen C, Yang F, Schneeloch J, Zhong R, Gu G, Fu L, Zhang Y Y, Ding H, Gao H J 2020 Science 367 189
 Google Scholar
Google Scholar
[64] Wang Q Y, Li Z, Zhang W H, Zhang Z C, Zhang J S, Li W, Ding H, Ou Y B, Deng P, Chang K, Wen J, Song C L, He K, Jia J F, Ji S H, Wang Y Y, Wang L L, Chen X, Ma X C, Xue Q K 2012 Chin. Phys. Lett. 29 037402
[65] He S L, He J F, Zhang W H, Zhao L, Liu D F, Liu X, Mou D X, Ou Y B, Wang Q Y, Li Z, Wang L L, Peng Y Y, Liu Y, Chen C Y, Yu L, Liu G D, Dong X L, Zhang J, Chen C T, Xu Z Y, Chen X, Ma X C, Xue Q K, Zhou X J 2013 Nat. Mater. 12 605
[66] Tan S Y, Zhang Y, Xia M, Ye Z R, Chen F, Xie X, Peng R, Xu D F, Fan Q, Xu H C, Jiang J, Zhang T, Lai X C, Xiang T, Hu J P, Xie B P, Feng D L 2013 Nat. Mater. 12 634
[67] Song Q, Yu T L, Lou X, Xie B P, Xu H C, Wen C H P, Yao Q, Zhang S Y, Zhu X T, Guo J D, Peng R, Feng D L 2019 Nat. Commun. 10 758
[68] Fan Q, Zhang W H, Liu X, Yan Y J, Ren M Q, Peng R, Xu H C, Xie B P, Hu J P, Zhang T, Feng D L 2015 Nat. Phys. 11 946
[69] Agterberg D F, Shishidou T, O’Halloran J, Brydon P M R, Weinert M 2017 Phys. Rev. Lett. 119 267001
[70] Liu C F, Wang Z Q, Gao Y, Liu X Q, Liu Y, Wang Q H, Wang J 2019 Phys. Rev. Lett. 123 036801
[71] Ge Z Z, Yan C H, Zhang H M, Agterberg D, Weinert M, Li L 2019 Nano Lett. 19 2497
[72] Beaird R, Vekhter I, Zhu J X 2012 Phys. Rev. B 86 140507(R)
[73] Song S Y, Martiny J H J, Kreisel A, Andersen B M, Seo J 2020 Phys. Rev. Lett. 124 117001
[74] Hu X, Ting C S, Zhu J X 2009 Phys. Rev. B 80 014523
[75] Peng R, Shen X P, Xie X, Xu H C, Tan S Y, Xia M, Zhang T, Cao H Y, Gong X G, Hu J P, Xie B P, Feng D L 2014 Phys. Rev. Lett. 112 107001
[76] Zhang Y, Lee J J, Moore R G, Li W, Yi M, Hashimoto M, Lu D H, Devereaux T P, Lee D H, Shen Z X 2016 Phys. Rev. Lett. 117 117001
[77] Satoshi K, Yukio T 2000 Rep. Prog. Phys. 63 1641
[78] Wang Z F, Zhang H M, Liu D F, Liu C, Tang C J, Song C L, Zhong Y, Peng J P, Li F S, Nie C N, Wang L L, Zhou X J, Ma X C, Xue Q K, F. Liu 2016 Nat. Mater. 15 968
[79] Liu W Y, Cao L, Zhu S, Kong L, Wang G, Papaj M, Zhang P, Liu Y, Chen H, Li G, Yang F, Kondo T, Du S, Cao G, Shin S, Fu L, Yin Z, Gao H J, Ding H 2019 arXiv: 1907.00904
[80] Yuan Y, Pan J, Wang X, Fang Y, Song C, Wang L, He K, Ma X, Zhang H, Huang F, Li W, Xue Q K 2019 Nat. Phys. 15 1046
[81] Jiang K, Dai X, Wang Z 2019 Phys. Rev. X 9 011033
[82] Yin J X, Wu Z, Wang J H, Ye Z Y, Gong J, Hou X Y, Shan L, Li A, Liang X J, Wu X X, Li J, Ting C S, Wang Z Q, Hu J P, Hor P H, Ding H, Pan S H 2015 Nat. Phys. 11 543
-
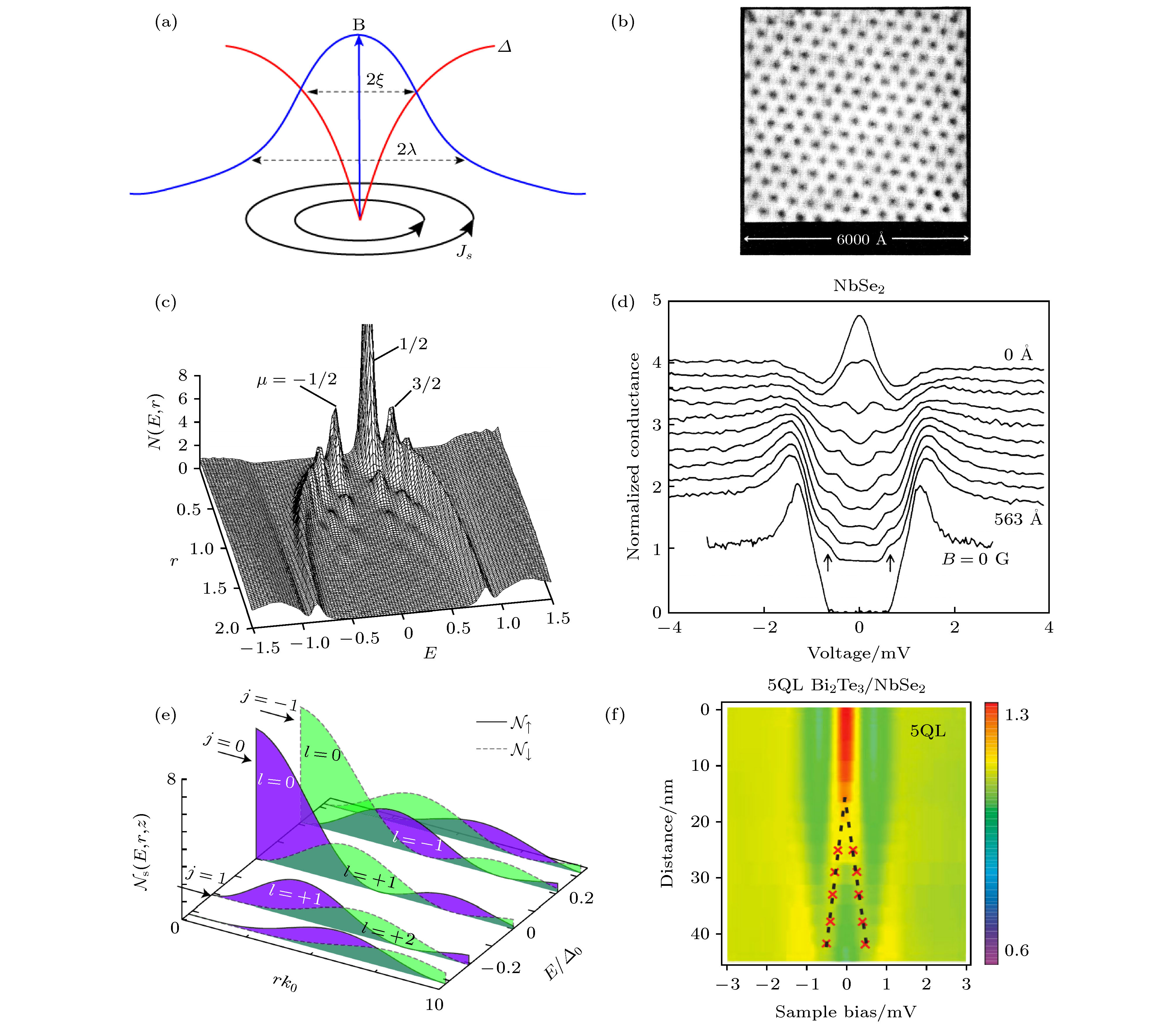
图 1 超导体磁通束缚态 (a) 磁通涡旋的示意图; (b) NbSe2的磁通晶格图像[22]; (c)理论计算的s波超导体分立的磁通束缚态及其空间分布[24]; (d) 实验测量的NbSe2从磁通中心向外的微分电导谱[23]; (e) 理论计算的拓扑超导体磁通态和空间、自旋分布情况[44]; (f) 5层Bi2Te3/NbSe2异质结的磁通的微分电导谱[14], 零能模在磁通中心一段距离内都存在
Fig. 1. Bound states in the vortex core of superconductor: (a) Sketch of a magnetic vortex (b) vortex lattice measured on NbSe2; (c) calculated discrete bound states near the vortex core of s-wave superconductor; (d) a seris of spectra measured near the vortex center of NbSe2; (e) wave functions of several low-energy quasiparticle excitations in a vortex of topological superconductor; (f) color plot of a set of dI/dV spectra measured along the vortex core on 5 QL Bi2Te3/NbSe2 heterostruture. Majorana zero mode exists within a certain distance near the vortex center.
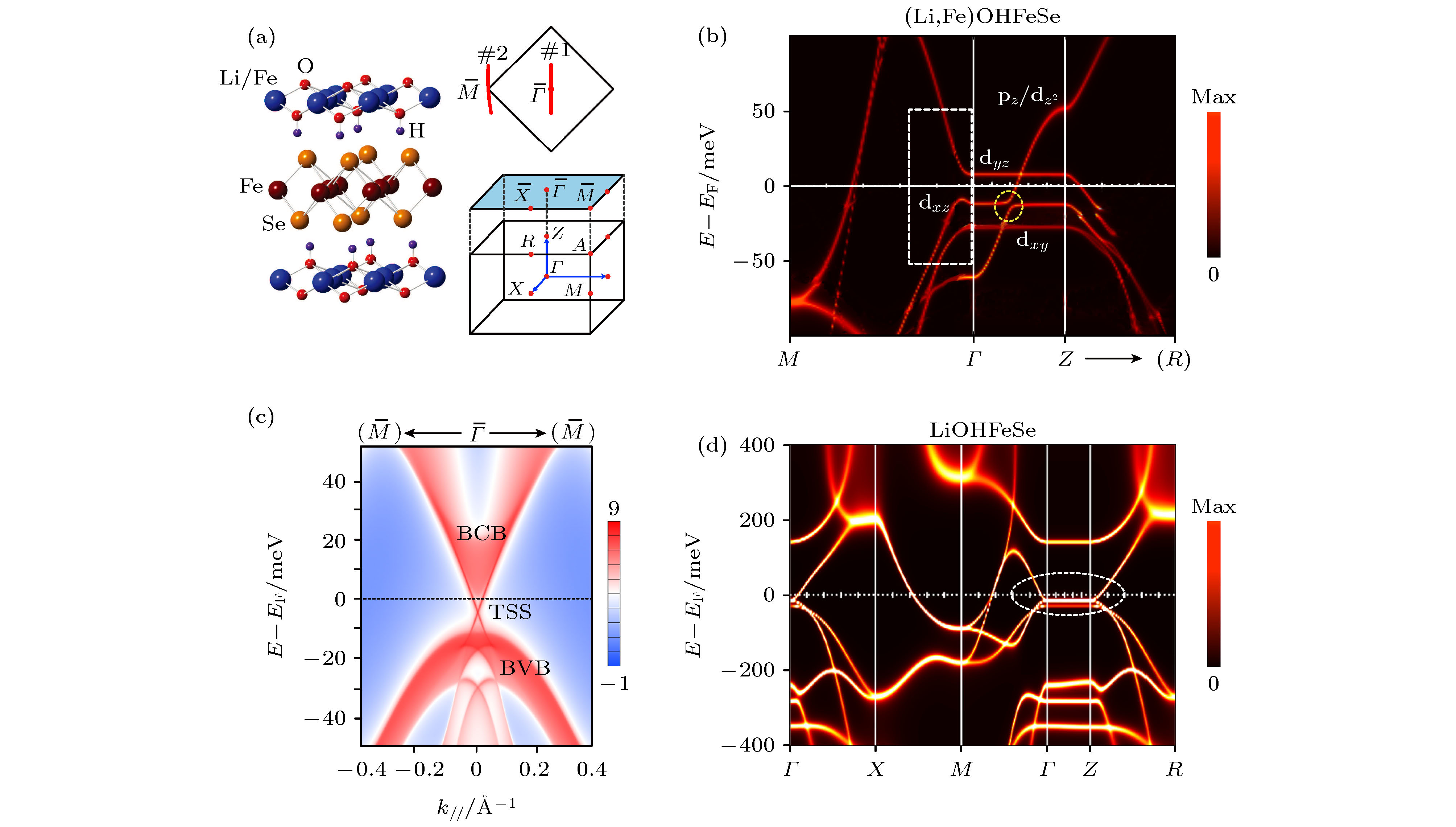
图 2 (Li, Fe)OHFeSe的能带结构和拓扑表面态 (a) (Li, Fe)OHFeSe的晶体结构、体态和(001)表面的布里渊区; (b)利用DFT+DMFT计算的(Li0.75Fe0.25)OHFeSe沿着M-Γ-Z-(R)方向的能带结构; (c)沿
$ \overline {\varGamma } $ -$ \overline {M} $ 方向在(001)面上计算的体态和狄拉克锥状的拓扑表面态; (d) LiOHFeSe在无自旋轨道耦合且处于顺磁PM状态下的能带结构Fig. 2. Band structure and topological surface states of (Li, Fe)OHFeSe: (a) The crystal structure and bulk & (001) surface Brillouin zone of (Li, Fe)OHFeSe; (b) band structure of (Li0.75Fe0.25)OHFeSe along M-Γ-Z-(R) direction, represented by spectral functions calculated by density functional theory (DFT) combined with dynamical mean-field theory (DMFT) methods; (c) calculated bulk and Dirac-cone-like topological surface states on the (001) surface along the
$ \overline {\varGamma }-\overline {M} $ direction; (d) band structure of LiOHFeSe in the PM state without spin orbital coupling (SOC).图 3 (Li0.84Fe0.16)OHFeSe的角分辨光电子实验测量 (a) 沿着图2(a)中切割线#1的方向穿过
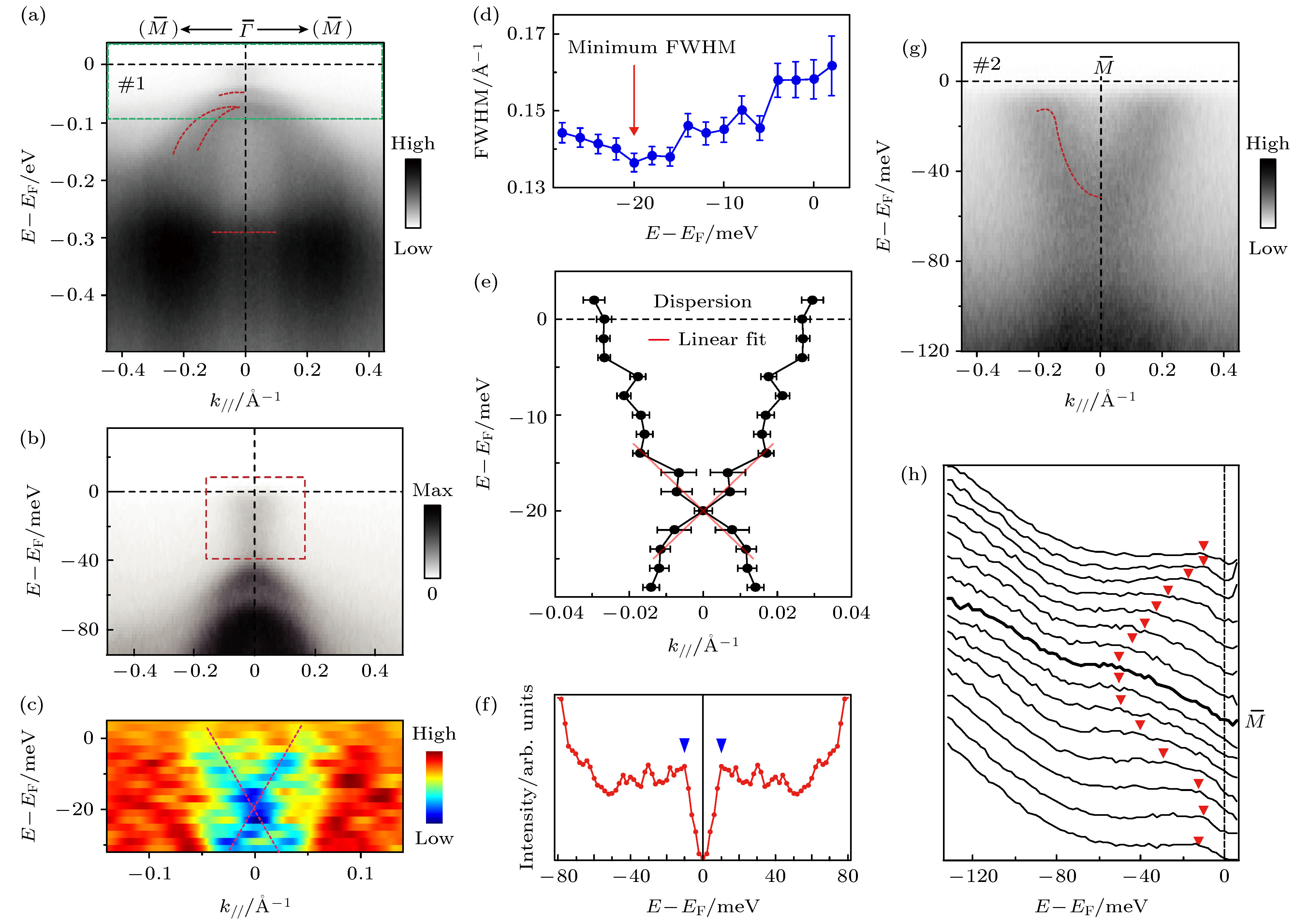
$ \overline {\varGamma } $ 点测量的光电子能谱; (b) 在图(a)中$ \overline {\varGamma } $ 点费米能量附近绿色虚线框中放大的数据; (c) 图(b)红色虚线框区域的光电子能谱的二阶导数, 可以看到类似狄拉克锥的色散; (d) 拟合得到的作为能量函数的峰的半高宽; (e)从数据中提取的E-k色散以及交叉点处的线性拟合; (f)$ \overline {M} $ 点电子口袋附近的对称化的能量分布曲线, 可以观察到约10 meV的超导能隙; (g) 沿图2(a)中切割线#2穿过$ \overline {M} $ 点的光电子能谱; (h) 图(d)中数据除以费米-狄拉克分布后的能量分布曲线(EDCs). 所有数据均在5.6 K温度下用21.2 eV能量的光子测量Fig. 3. ARPES measurement of (Li0.84Fe0.16)OHFeSe: (a) Photoemission intensity across
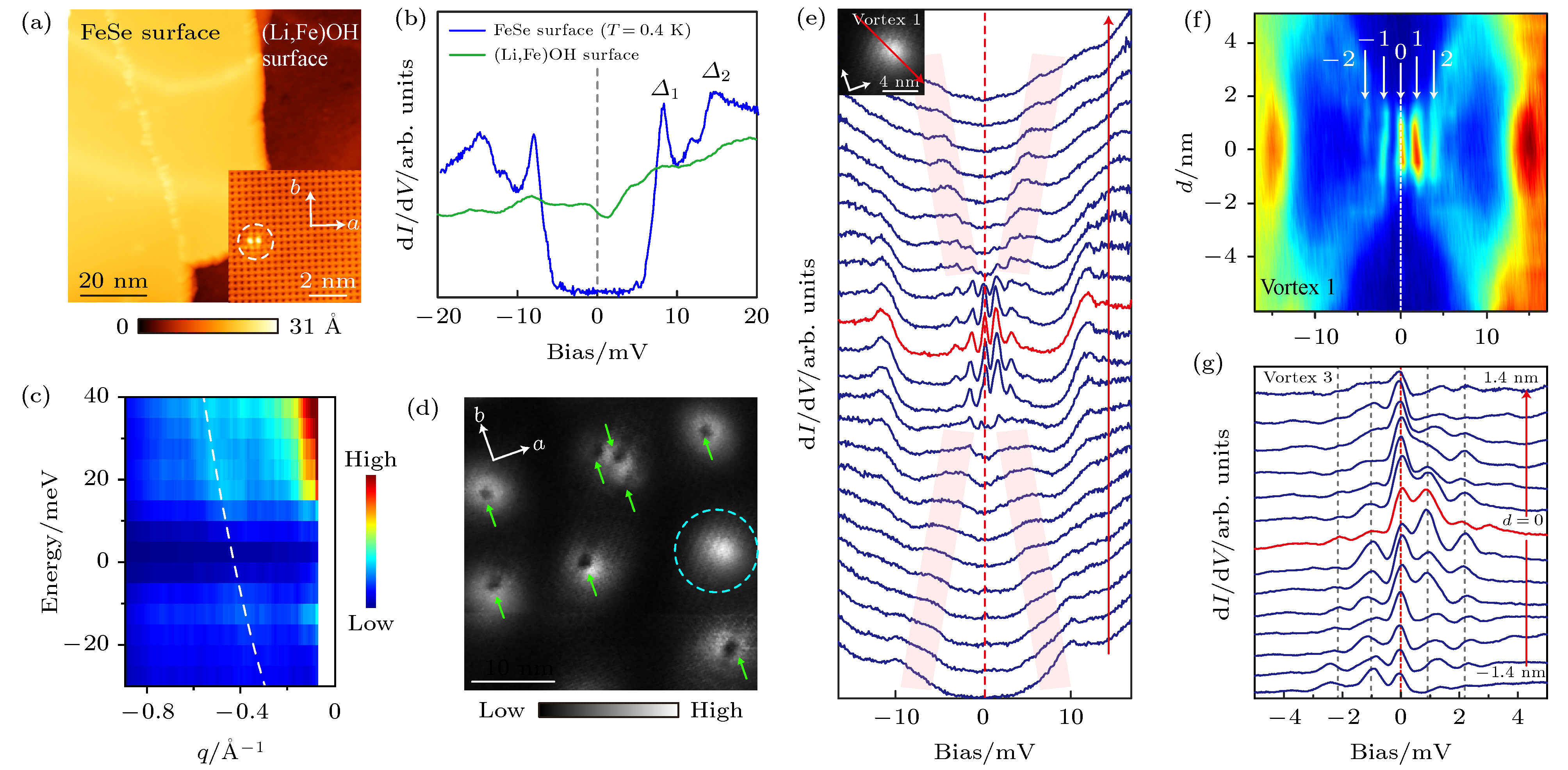
$ \overline {\varGamma } $ along cut #1 in Fig.2(a); (b) an enlargement of data corresponds to the green dashed rectangle in panel (a) near EF at$ \overline {\varGamma } $ point; (c) second derivative of the photoemission intensity in the marked region of panel (b), a Dirac-cone like dispersion can be seen; (d) the FWHM obtained from fitting, as a function of energy; (e) E-k dispersion extracted from the data, and the linear fit around the crossing point; (f) symmetrized energy distribution curve (EDC) near the Fermi crossing of the M pocket, where a superconducting gap of ~10 meV is observed; (g) photoemission intensity taken along cut #2 across$ \overline {M} $ in Fig.2(a); (h) the energy distribution curves (EDCs) of the data in panel (d) after dividing by Fermi-Dirac distribution. All the data were measured at 5.6 K using 21.2 eV photons.图 4 (Li0.84Fe0.16)OHFeSe样品的形貌、超导能隙、准粒子干涉和磁通束缚态 (a)解理后样品表面的形貌图, 右下插图是FeSe面原子晶格(晶格常数a0 = 3.8 Å). 虚线圆圈内是哑铃状杂质; (b) FeSe和(Li, Fe)OH面的微分电导dI/dV谱; (c)利用QPI测量的
$ \overline {M} $ 点电子型能带的色散, 虚线是抛物线拟合; (d) FeSe面, B = 10 T下的零偏压电导成像. 钉扎的磁通用箭头标记, 白色圆圈处是“自由”磁通; (e) 穿过自由磁通1的一系列隧道谱, 可清晰看到磁通中心附近分立的束缚态; (f)对应图(e)中隧道谱的颜色图表示, 箭头标出了分立的磁通态; (g) 磁通中心附近较小范围内的隧道谱, 可看出零能峰的位置保持不变Fig. 4. Topography, superconducting gap, QPI and vortex bound states of (Li0.84Fe0.16)OHFeSe: (a) Topographic image of a cleaved film. Inset: the lattice of FeSe surface (a0 = 3.8 Å). A dimer-like defect is marked by the circle; (b) typical dI/dV spectra taken on FeSe and (Li0.84Fe0.16)OH surface; (c) electron-like Energy dispersion measured by QPI at
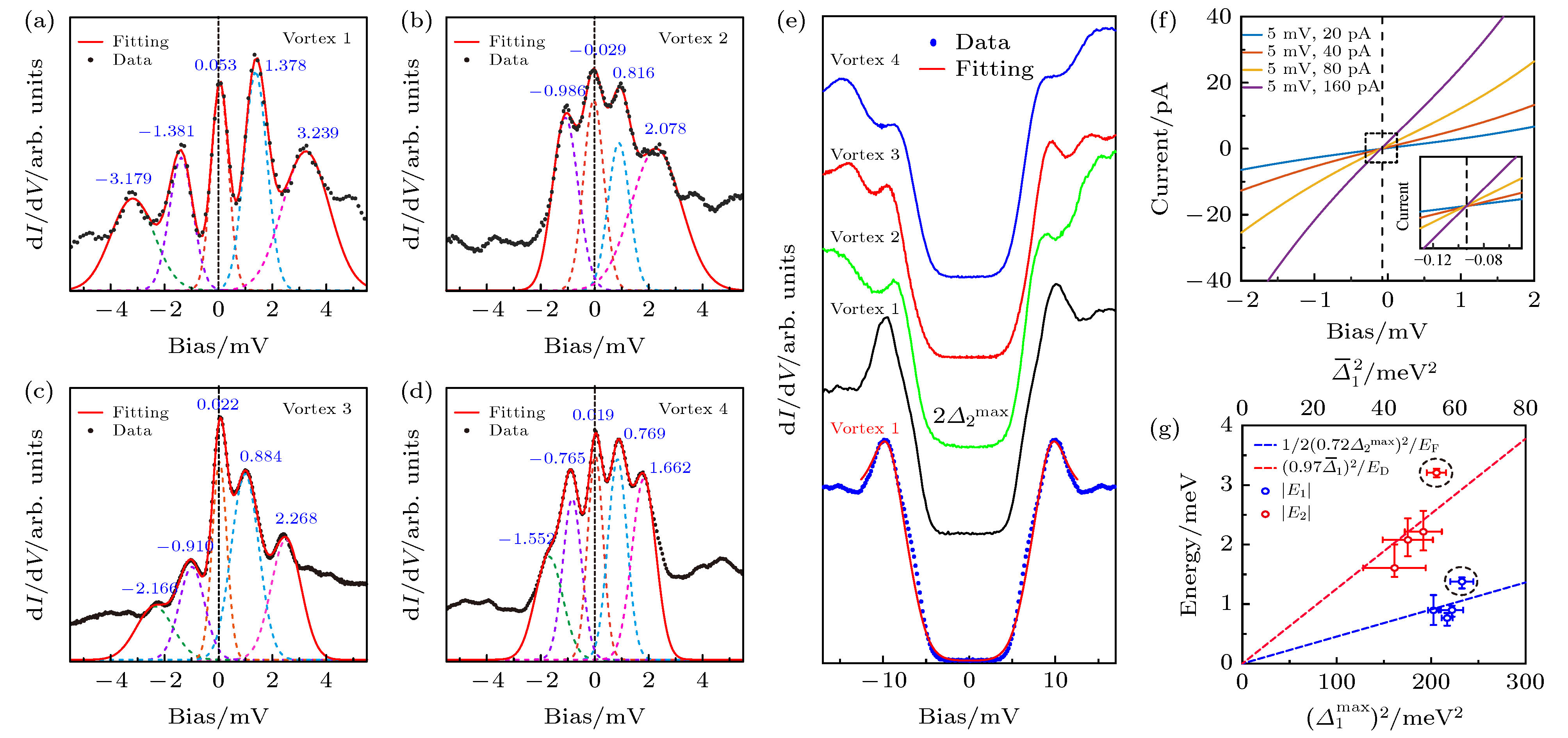
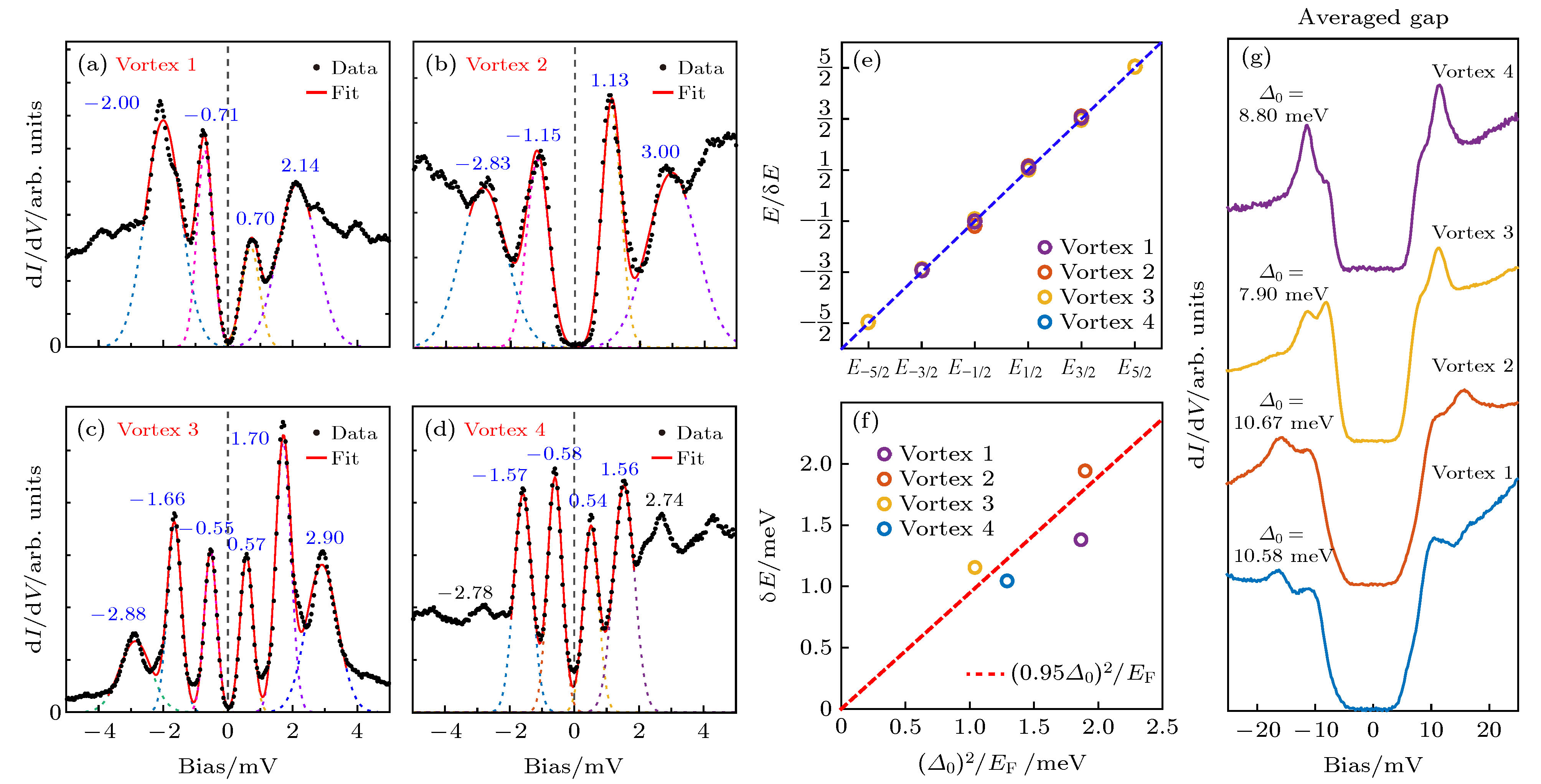
$ \overline {M} $ point. Dashed curve is a parabolic fit; (d) zero bias conductance map on FeSe surface under B = 10 T. Pinned-vortices are indicated by arrows. The dashed circle encloses a free vortex; (e) dI/dV spectra taken across the free Vortex 1 and discrete low-energy states were observed in the vortex core; (f) color plot of the spatial dependence of the dI/dV spectra shown in panels (e) and arrows indicate the positions of discrete vortex states; (g) dI/dV spectra taken at the small range near the vortex and the zero-bias peak keeps unchanged.图 5 磁通束缚态的定量特性 (a)—(d) 四个不同磁通中心的微分电导谱, 红色实线是多高斯函数拟合, 虚线为每个高斯函数对应的峰; (e) 磁通1—4出现区域的局域超导能隙. 最下方是磁通1对称化后的dI/dV谱(蓝色曲线)和各向异性能隙函数拟合(红色曲线); (f) 通过不同隧穿势垒下的I-V谱对隧道谱零偏压点的标定; (g) 能量|E2|, |E1|分别以(
$ \overline {{\varDelta }_{1}} $ )2, (Δ2max)2作为变量得到的拟合结果, 其中虚线代表线性拟合的结果Fig. 5. Quantitative characterization of the vortex core states: (a)–(d) Summed low-energy dI/dV spectra taken near the centers of Vortex 1–4. Red solid curves are the fits to multiple Gaussian peaks (dashed curves are the individual peaks); (e) local superconducting gaps measured where Vortex 1–4 emerge. The bottom curves are the symmetrized dI/dV spectrum (blue one) for vortex 1 after subtracting a background slope and corresponding fit (red one) using anisotropic gap function; (f) calibration for the zero bias offset using a set of I-V spectra taken at different setpoints; (g) plots of
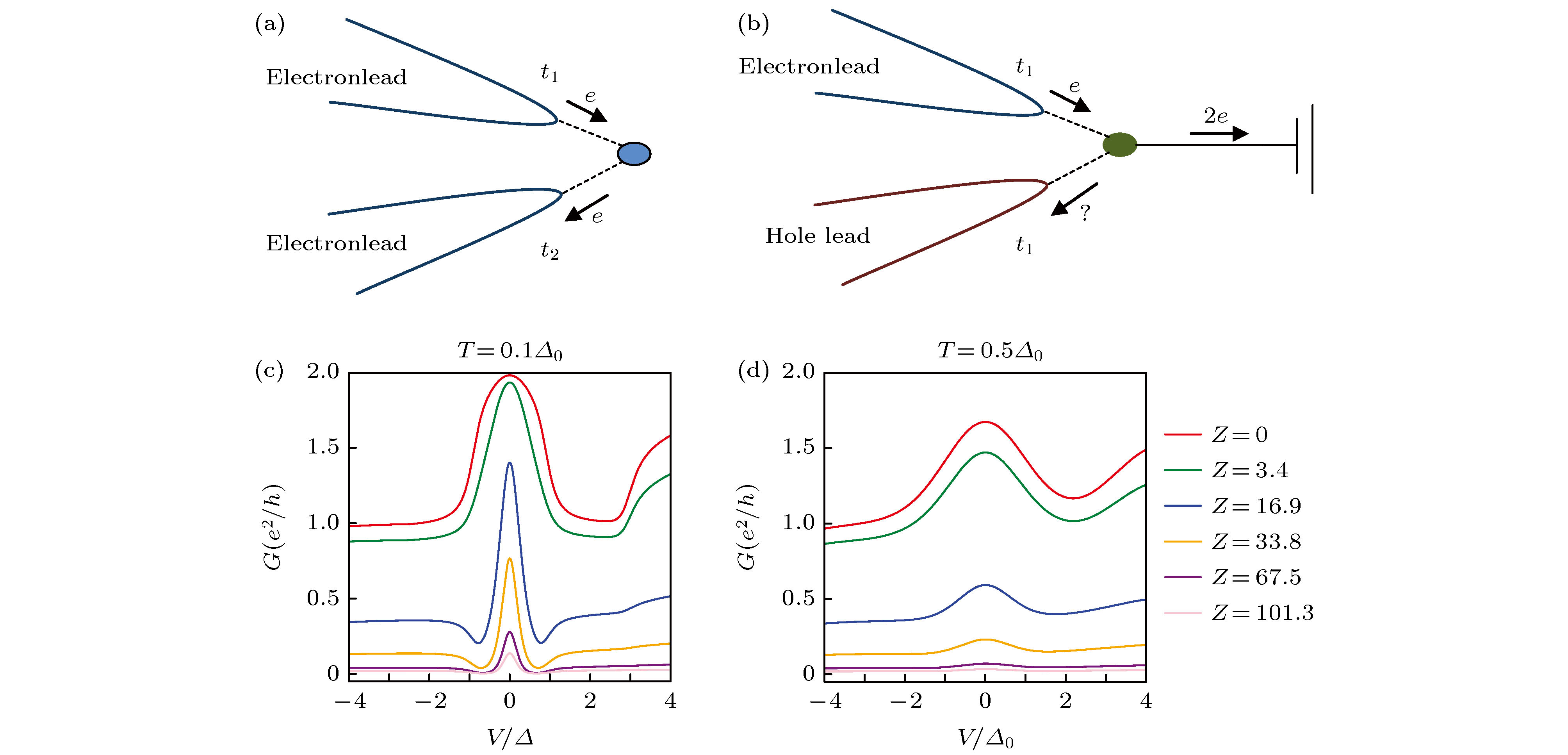
$ |{E}_{2}| $ (red circles) as a function of ($ \overline {{\varDelta }_{1}} $ )2, and$ |{E}_{1}| $ (blue circles) as a function of$ {({\varDelta }_{2}^{\max})}^{2} $ . Dashed lines are the linear fitting (see legend).图 6 共振Andreev反射与Majorana零能模的量子化电导 (a)经典共振隧穿[41]; (b) Majorana零能模诱导的共振Andreev反射[41]; (c), (d)实际测量的Majorana零能模电导值与温度和隧穿耦合强度的关系[42]
Fig. 6. Resonant Andreev reflection and quantized conductance of Majorana zero mode: (a) Conventional resonant tunneling; (b) Majorana zero mode induced resonant Andreev reflection (MIRAR); (c), (d) the relationship between Majorana zero mode conductance and temperature, tunneling coupling strength.
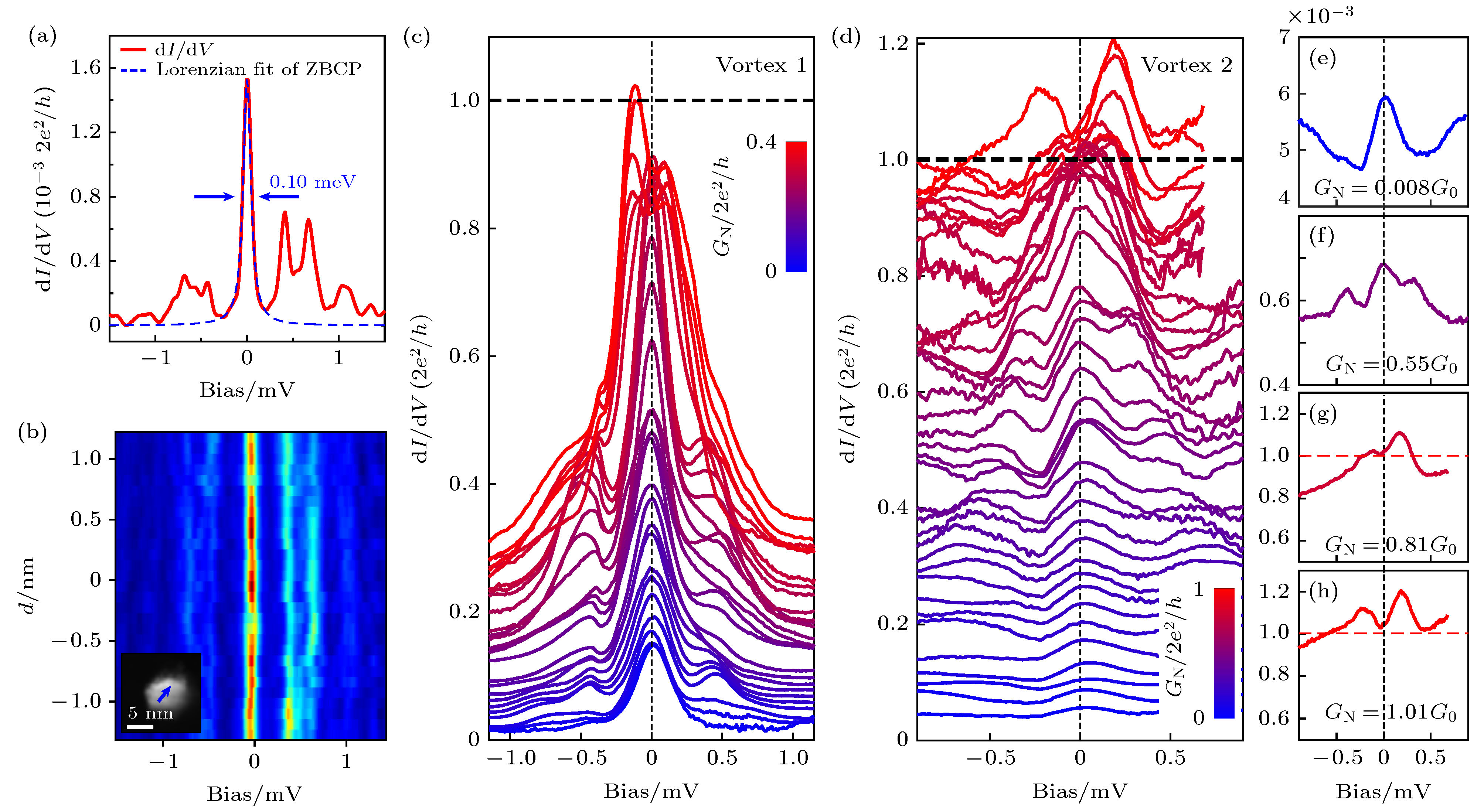
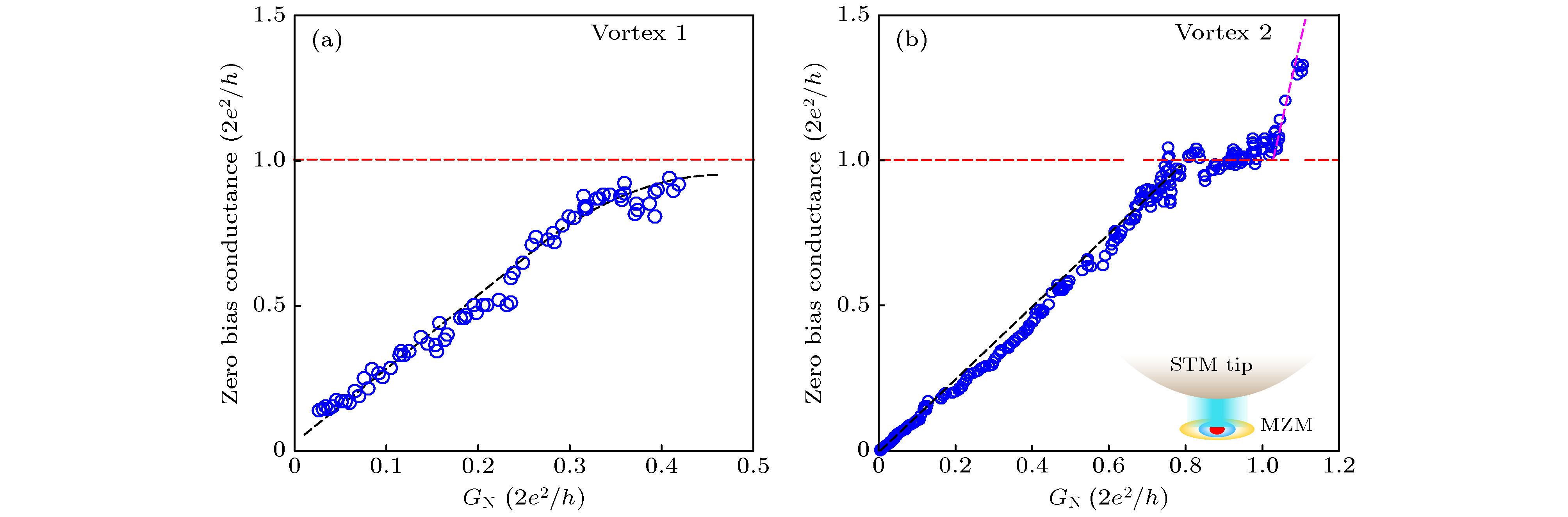
图 7 (a)磁通中心处的微分电导谱, 相应的隧穿电导是校正过的绝对值. 蓝色虚线: 利用洛伦兹函数来拟合零偏压峰, 相应的半高宽是0.10 meV; (b)图(a)中的微分电导谱的空间二维颜色示意图; (c), (d) 自由磁通1和2中心处隧道谱随GN的变化(其中GN定义为Iset/Vb, 对于磁通1为Vb = –1.7 mV, 磁通2为Vb = –0.9 mV); (e)—(f)对于磁通2, 不同GN下的四条典型的微分电导谱
Fig. 7. (a) Red curve: dI/dV spectrum at the core center. The tunneling conductance is calibrated by scaling to the numerical differential of the I/V curve. Blue dashed curve: Lorentzian fit to the ZBCP, with a FWHM = 0.10 meV; (b) spatial dependence of the dI/dV spectra in panel (a), shown in a false-color plot; (c), (d) evolution of the dI/dV spectra as a function of increased tunneling transmission for free vortex 1&2 reflected by GN = Iset/Vb (Vb = –1.7 mV for vortex 1 and Vb = –0.9 mV for vortex 2); (e)–(f) selected dI/dV spectra taken at different GN for vortex 2.
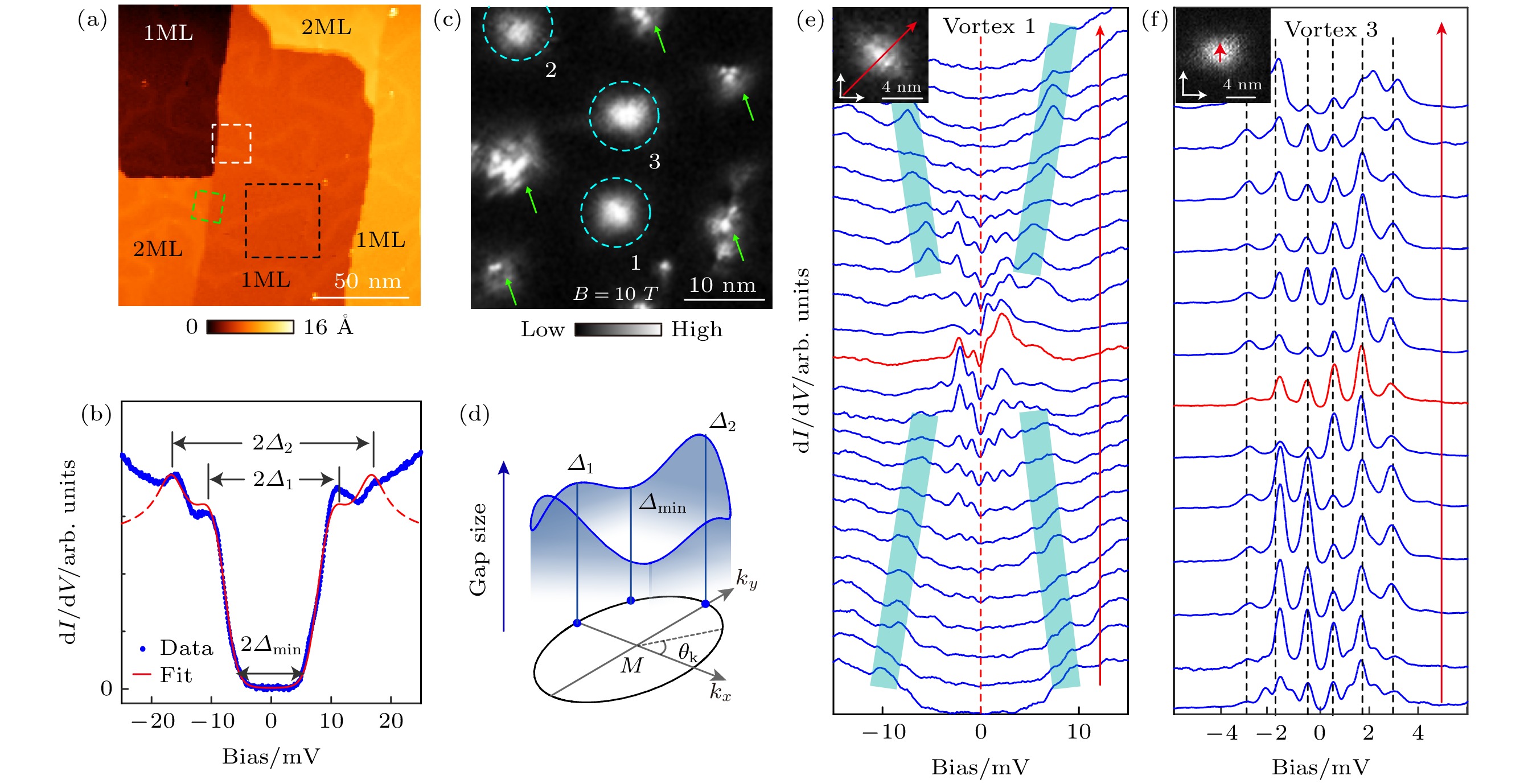
图 9 (a) SrTiO3衬底上生长的FeSe薄膜形貌(平均厚度1.3层); (b)单层FeSe薄膜的典型超导能隙谱(Vb = 30 mV, I = 60 pA, T = 4.2 K), 蓝色点为B = 0 T磁场下的实验数据, 红色曲线是拟合的结果; (c) B = 10 T时的零偏压微分电导成像, 绿色箭头所指的是杂质钉扎的磁通, 虚线圆圈里是未钉扎的自由磁通; (d) 布里渊区M点费米面上的能隙分布示意图. Δ2, Δ1和Δmin分别对应于两个局部能隙最大值以及一个能隙最小值, 并且tg(θk)=ky/kx; (e), (f) 穿越磁通1和3中心的路径上0.4 K温度下所测量的微分电导谱(等效电子温度Telec = 1.18 K), 显示出清晰分立的磁通态(无零偏压峰)
Fig. 9. (a) STM image of FeSe/SrTiO3 film with a thickness of ~1.3 ML; (b) typical gap spectrum (blue curve) of 1 ML FeSe (Vb = 30 mV, I = 60 pA, T = 4.2 K) taken at B = 0 T and the fitted gap is shown in red curve; (c) zero-bias dI/dV mapping taken at B = 10 T. Green arrows indicate surface defects and the pinned vortices, dashed circles indicate free vortices; (d) sketch of the gap distribution on the electron pocket at M. Δ2, Δ1 and Δmin correspond to the two local gap maxima and the gap minima, respectively, and tg(θk) = ky/kx; (e), (f) dI/dV spectra taken across Vortex 1 and 3 at T = 0.4 K (Telec = 1.18 K). Discrete vortex states (without zero bias peak) were observed.
图 10 磁通束缚态的定量拟合 (a)—(d)自由磁通1—4中心的低能量的微分电导谱. 其中红色的曲线是多个高斯峰拟合的结果(虚线是单个高斯峰); (e)通过除以磁通1—4中的束缚态的平均能量间隔δE得到的每个磁通中心的CdGM束缚态的归一化能量; (f)对于自由磁通1—4,
$ {({\varDelta }_{0})}^{2}/{E}_{\rm{F}} $ 与能量间隔δE的关系, 虚线是线性的拟合曲线; (g)是自由磁通1—4出现位置处的不加磁场时超导能隙, 平均超导能隙的大小Δ0是通过函数拟合得到Fig. 10. Quantitative fitting of vortex bound states: (a)–(d) Low energy spectra of free Vortices 1–4. Red curves are multiple Gaussian-peak fits (Dashed curves are individual peaks); (e) normalized energy of the CdGM state of Vortices 1–4, via dividing the averaged δE of each vortex; (f) the relation of
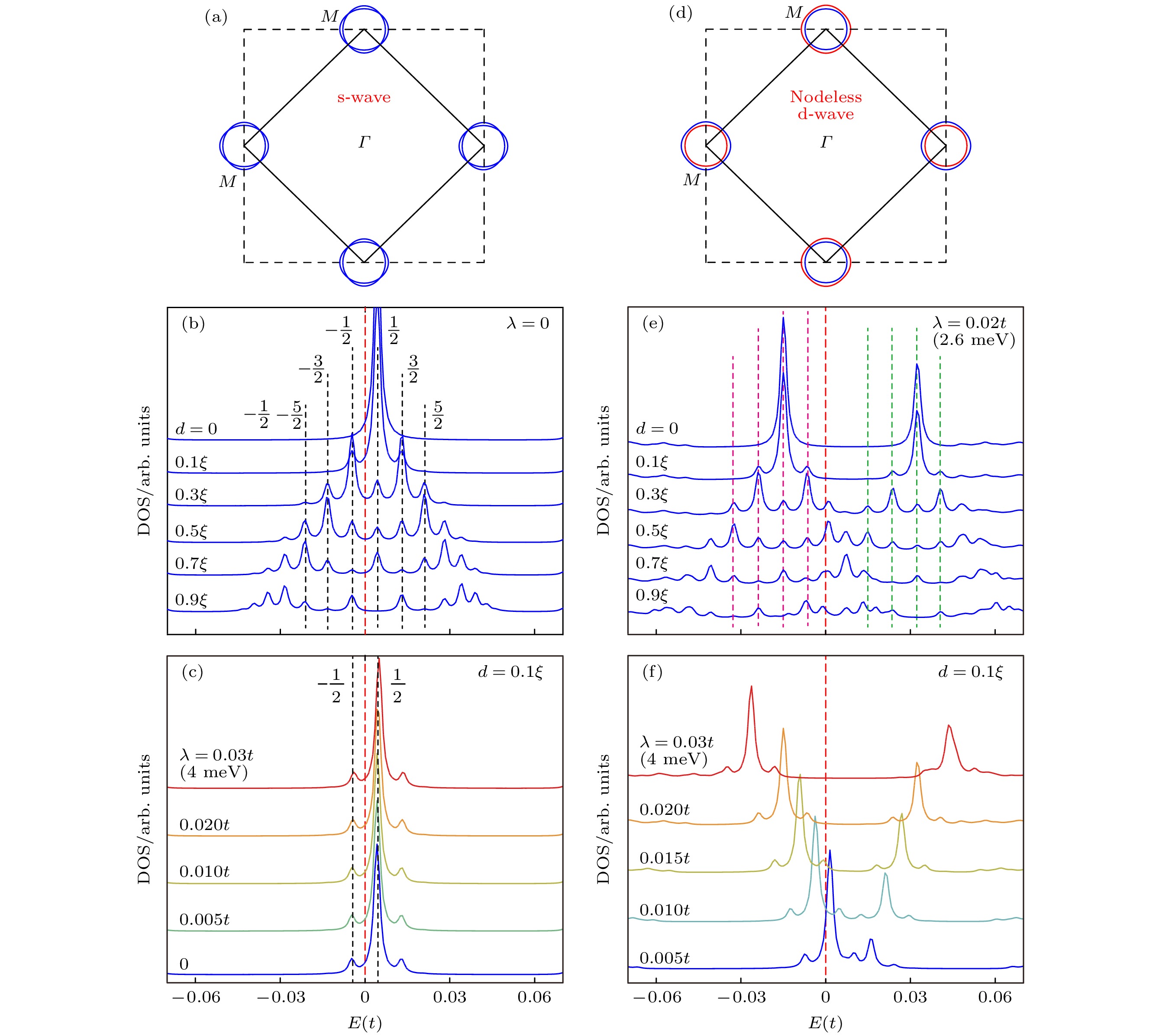
$ {({\varDelta }_{0})}^{2}/{E}_{\rm{F}} $ and δE for Vortices 1–4, dashed line is the linear fitting. (g) superconducting gap spectra taken at the area where Vortex 1–4 appear (B = 0 T). The mean gap sizes (Δ0) are obtained from the gap fitting.图 11 理论计算的s波和无节点d波的磁通束缚态 (a), (d) s波和无节点d波配对的费米面示意图; (b), (e)分别是在距离磁通中心不同距离处没有自旋轨道耦合的s波配对、自旋轨道耦合强度λ = 0.02t下的无节点d波配对的磁通态情形(ξ是相干长度, λ是自旋轨道耦合强度); (c), (f)分别是距离磁通中心固定距离d = 0.1ξ的不同自旋轨道耦合强度下的情形 (c)是不同自旋轨道耦合强度λ的s波配对, (f)是无节点d波配对
Fig. 11. Calculated vortex states under s-wave and nodeless d-wave pairing. Sketch of the Fermi surface for (a) s-wave (d) nodeless d-wave pairing. (b), (e) Calculated vortex states at different distance to the core center for (b) s-wave (e) nodeless d-wave with λ = 0.02t (ξ is the coherence length and λ is SOC strength). (c), (f) Calculated vortex states under s-wave (c) and nodeless d-wave (f) pairing at d = 0.1 ξ, with various SOC strength.
-
[1] Caroli C, de Gennes P G, Matricon J 1964 Phys. Lett. 9 307
[2] Volovik G E 1999 JETP Lett. 70 609
[3] Read N, Green D 2000 Phys. Rev. B 61 10267
[4] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057
[5] Alicea J 2012 Rep. Prog. Phys. 75 076501
[6] Leijnse M, Flensberg K 2012 Semicond. Sci. Technol. 27 124003
[7] Beenakker C W J 2013 Annu. Rev. Condens. Matter Phys. 4 113
[8] Sato M, Ando Y 2017 Rep. Prog. Phys. 80 076501
[9] Kitaev A 2003 Ann. Phys. 303 2
[10] Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083
[11] Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407
[12] Wang M X, Liu C, Xu J P, Yang F, Miao L, Yao M Y, Gao C L, Shen C, Ma X, Chen X, Xu Z A, Liu Y, Zhang S C, Qian D, Jia J F, Xue Q K 2012 Science 336 52
 Google Scholar
Google Scholar
[13] Xu J P, Liu C, Wang M X, Ge J, Liu Z L, Yang X, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001
[14] Xu J P, Wang M X, Liu Z L, Ge J F, Yang X, Liu C, Xu Z A, Guan D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001
[15] Sun H H, Zhang K W, Hu L H, Li C, Wang G Y, Ma H Y, Xu Z A, Gao C L, Guan D D, Li Y Y, Liu C, Qian D, Zhou Y, Fu L, Li S C, Zhang F C, Jia J F 2016 Phys. Rev. Lett. 116 257003
[16] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers EPAM, Kouwenhoven L P 2012 Science 336 1003
 Google Scholar
Google Scholar
[17] Das A, Ronen Y, Most Y, Oreg Y, Heiblum M, Shtrikman H 2012 Nat. Phys. 8 887
[18] Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602
 Google Scholar
Google Scholar
[19] Jeon S, Xie Y, Li J, Wang Z, Bernevig B A, Yazdani A 2017 Science 358 772
 Google Scholar
Google Scholar
[20] Zhang H, Liu C X, Gazibegovic S, Xu D, Logan J A, Wang G, van Loo N, Bommer J D S, de Moor M W A, Car D, Op Het Veld R L M, van Veldhoven P J, Koelling S, Verheijen M A, Pendharkar M, Pennachio D J, Shojaei B, Lee J S, Palmstrom C J, Bakkers E P A M, Sarma S D, Kouwenhoven L P 2018 Nature 556 74
[21] Suderow H, Guillamón I, Rodrigo J G, Vieira S 2014 Supercond. Sci. Technol. 27 063001
[22] Hess H F, Robinson R B, Dynes R C, Valles J M, Jr Waszczak J V 1989 Phys. Rev. Lett. 62 214
[23] Hess H F, Robinson R B, Waszczak J V 1990 Phys. Rev. Lett. 64 2711
[24] Hayashi N, Isoshima T, Ichioka M, Machida K 1998 Phys. Rev. Lett. 80 2921
[25] Song C L, Wang Y L, Cheng P, Jiang Y P, Li Wei, Zhang T, Li Z, He K, Wang L L, Jia J F, Hung H H, Wu C J, Ma X C, Chen X, Xue Q K 2011 Science 332 1410
 Google Scholar
Google Scholar
[26] Hanaguri T, Kitagawa K, Matsubayashi K, Mazaki Y, Uwatoko Y, Takagi H 2012 Phys. Rev. B 85 214505
[27] Zhou B B, Misra S, da Silva Neto E H, Aynajian P, Baumbach R E, Thompson J D, Bauer E D Yazdani A 2013 Nat. Phys. 9 474
[28] Hao N, Hu J 2014 Phys. Rev. X 4 031053
[29] Wang Z, Zhang P, Xu G, Zeng L K, Miao H, Xu X, Qian T, Weng H, Richard P, Fedorov A V, Ding H, Dai X, Fang Z 2015 Phys. Rev. B 92 115119
[30] Xu G, Lian B, Tang P, Qi X L, Zhang S C 2016 Phys. Rev. Lett. 117 047001
[31] 郝宁, 胡江平 2018 67 207101
 Google Scholar
Google Scholar
Hao N, Hu J P 2018 Acta Phys. Sin. 67 207101
 Google Scholar
Google Scholar
[32] Chen M Y, Chen X, Yang H, Du Z, Zhu X, Wang E, Wen H H 2018 Nat. Commun. 9 970
[33] Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333
 Google Scholar
Google Scholar
[34] Machida T, Sun Y, Pyon S, Takeda S, Kohsaka Y, Hanaguri T, Sasagawa T, Tamegai T 2019 Nat. Mater. 18 811
[35] Kong L Y, Zhu S Y, Papaj M, Chen H, Cao L, Isobe H, Xing Y Q, Liu W Y, Wang D F, Fan P, Sun Y J, Du S X, Schneeloch J, Zhong R D, Gu G D, Fu L, Gao H J, Ding H 2019 Nat. Phys. 15 1181
[36] Zhang P, Yaji K, Hashimoto T, Ota Y, Kondo T, Okazaki K, Wang Z, Wen J, Gu G D, Ding H, Shin S 2018 Science 360 182
 Google Scholar
Google Scholar
[37] Chiu C K, Machida T, Huang Y, Hanaguri T, Zhang F C 2020 Sci. Adv. 6 eaay0443
 Google Scholar
Google Scholar
[38] Balatsky A V 2006 Rev. Mod. Phys. 78 373
[39] Lee E J H, Jiang X, Aguado R, Katsaros G, Lieber C M, de Franceschi S 2012 Phys. Rev. Lett. 109 186802
[40] Levy N, Zhang T, Ha J, Sharifi F, Talin A A, Kuk Y, Stroscio J A 2013 Phys. Rev. Lett. 110 117001
[41] Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001
[42] Setiawan F, Liu C X, Sau J D, Sarma S D 2017 Phys. Rev. B 96 184520
[43] He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001
[44] Kawakami T, Hu X 2015 Phys. Rev. Lett. 115 177001
[45] Hu L H, Li C, Xu D H, Zhou Y, Zhang F C 2016 Phys. Rev. B 94 224501
[46] Liu Q, Chen C, Zhang T, Peng R, Yan Y J, Wen C H P, Lou X, Huang Y L, Tian J P, Dong X L, Wang G W, Bao W C, Wang Q H, Yin Z P, Zhao Z X, Feng D L 2018 Phys. Rev. X 8 041056
[47] Chen C, Liu Q, Zhang T Z, Li D, Shen P P, Dong X L, Zhao Z X, Zhang T, Feng D L 2019 Chin. Phys. Lett. 36 057403
[48] Chen C, Liu Q, Bao W C, Yan Y J, Wang Q H, Zhang T, Feng D L 2020 Phys. Rev. Lett. 124 097001
[49] Dong X, Jin K, Yuan D, Zhou H, Yuan J, Huang Y, Hua W, Sun J, Zheng P, Hu W, Mao Y, Ma M, Zhang G, Zhou F, Zhao Z 2015 Phys. Rev. B 92 064515
[50] Lu X F, Wang N Z, Wu H, Wu Y P, Zhao D, Zeng X Z, Luo X G, Wu T, Bao W, Zhang G H, Huang F Q, Huang Q Z, Chen X H 2015 Nat. Mater. 14 325
[51] Niu X H, Peng R, Xu H C, Yan Y J, Jiang J, Xu D F, Yu T L, Song Q, Huang Z C, Wang Y X, Xie B P, Lu X F, Wang N Z, Chen X H, Sun Z, Feng D L 2015 Phys. Rev. B 92 060504(R)
[52] L. Zhao, Liang A J, Yuan D N, Hu Y, Liu D F, Huang J W, He S L, Shen B, Xu Y, Liu X, Yu L, Liu G D, Zhou H X, Huang Y L, Dong X L, Zhou F, Liu K, Lu Z Y, Zhao Z X, Chen C T, Xu Z Y, Zhou X J 2016 Nat. Commun. 7 10608
[53] Georges A, Kotliar G, Krauth W, Rozenberg M J 1996 Rev. Mod. Phys. 68 13
[54] Kotliar G, Savrasov S Y, Haule K, Oudovenko V S, Parcollet O, Marianetti C A 2006 Rev. Mod. Phys. 78 865
[55] Huang Y L, Feng Z P, Ni S L, Li J, Hu W, Liu S B, Mao Y Y, Zhou H X, Zhou F, Jin K, Wang H B, Yuan J, Dong X L, Zhao Z X 2017 Chin. Phys. Lett. 34 077404
[56] Huang Y L, Feng Z P, Yuan J, Hu W, Li J, Ni S L, Liu S B, Mao Y Y, Zhou H X, Wang H B, Zhou F, Zhang G M, Jin K, Dong X L, Zhao Z X 2017 arXiv: 1711.02920
[57] Yi M, Liu Z K, Zhang Y, Yu R, Zhu J X, Lee J J, Moore R G, Schmitt F T, Li W, Riggs S C, Chu J H, Lv B, Hu J, Hashimoto M, Mo S K, Hussain Z, Mao Z Q, Chu C W, Fisher I R, Si Q, Shen Z X, Lu D H 2015 Nat. Commun. 6 7777
[58] Yan Y J, Zhang W H, Ren M Q, Liu X, Lu X F, Wang N Z, Niu X H, Fan Q, Miao J, Tao R, Xie B P, Chen X H, Zhang T, Feng D L 2016 Phys. Rev. B 94 134502
[59] Ren M Q, Yan Y J, Niu X H, Tao R, Hu D, Peng R, Xie B P, Zhao J, Zhang T, Feng D L 2017 Sci. Adv. 3 e1603238
 Google Scholar
Google Scholar
[60] Du Z Y, Yang X, Altenfeld D, Gu Q Q, Yang H, Eremin I, Hirschfeld P J, Mazin I I, Lin H, Zhu X Y, Wen H H 2018 Nat. Phys. 14 134
[61] Kells G, Meidan D, Brouwer P W 2012 Phys. Rev. B 86 100503
[62] Liu C X, Sau J D, Stanescu T D, Sarma S D 2017 Phys. Rev. B 96 075161
[63] Zhu S Y, Kong L, Cao L, Chen H, Papaj M, Du S, Xing Y, Liu W, Wang D, Shen C, Yang F, Schneeloch J, Zhong R, Gu G, Fu L, Zhang Y Y, Ding H, Gao H J 2020 Science 367 189
 Google Scholar
Google Scholar
[64] Wang Q Y, Li Z, Zhang W H, Zhang Z C, Zhang J S, Li W, Ding H, Ou Y B, Deng P, Chang K, Wen J, Song C L, He K, Jia J F, Ji S H, Wang Y Y, Wang L L, Chen X, Ma X C, Xue Q K 2012 Chin. Phys. Lett. 29 037402
[65] He S L, He J F, Zhang W H, Zhao L, Liu D F, Liu X, Mou D X, Ou Y B, Wang Q Y, Li Z, Wang L L, Peng Y Y, Liu Y, Chen C Y, Yu L, Liu G D, Dong X L, Zhang J, Chen C T, Xu Z Y, Chen X, Ma X C, Xue Q K, Zhou X J 2013 Nat. Mater. 12 605
[66] Tan S Y, Zhang Y, Xia M, Ye Z R, Chen F, Xie X, Peng R, Xu D F, Fan Q, Xu H C, Jiang J, Zhang T, Lai X C, Xiang T, Hu J P, Xie B P, Feng D L 2013 Nat. Mater. 12 634
[67] Song Q, Yu T L, Lou X, Xie B P, Xu H C, Wen C H P, Yao Q, Zhang S Y, Zhu X T, Guo J D, Peng R, Feng D L 2019 Nat. Commun. 10 758
[68] Fan Q, Zhang W H, Liu X, Yan Y J, Ren M Q, Peng R, Xu H C, Xie B P, Hu J P, Zhang T, Feng D L 2015 Nat. Phys. 11 946
[69] Agterberg D F, Shishidou T, O’Halloran J, Brydon P M R, Weinert M 2017 Phys. Rev. Lett. 119 267001
[70] Liu C F, Wang Z Q, Gao Y, Liu X Q, Liu Y, Wang Q H, Wang J 2019 Phys. Rev. Lett. 123 036801
[71] Ge Z Z, Yan C H, Zhang H M, Agterberg D, Weinert M, Li L 2019 Nano Lett. 19 2497
[72] Beaird R, Vekhter I, Zhu J X 2012 Phys. Rev. B 86 140507(R)
[73] Song S Y, Martiny J H J, Kreisel A, Andersen B M, Seo J 2020 Phys. Rev. Lett. 124 117001
[74] Hu X, Ting C S, Zhu J X 2009 Phys. Rev. B 80 014523
[75] Peng R, Shen X P, Xie X, Xu H C, Tan S Y, Xia M, Zhang T, Cao H Y, Gong X G, Hu J P, Xie B P, Feng D L 2014 Phys. Rev. Lett. 112 107001
[76] Zhang Y, Lee J J, Moore R G, Li W, Yi M, Hashimoto M, Lu D H, Devereaux T P, Lee D H, Shen Z X 2016 Phys. Rev. Lett. 117 117001
[77] Satoshi K, Yukio T 2000 Rep. Prog. Phys. 63 1641
[78] Wang Z F, Zhang H M, Liu D F, Liu C, Tang C J, Song C L, Zhong Y, Peng J P, Li F S, Nie C N, Wang L L, Zhou X J, Ma X C, Xue Q K, F. Liu 2016 Nat. Mater. 15 968
[79] Liu W Y, Cao L, Zhu S, Kong L, Wang G, Papaj M, Zhang P, Liu Y, Chen H, Li G, Yang F, Kondo T, Du S, Cao G, Shin S, Fu L, Yin Z, Gao H J, Ding H 2019 arXiv: 1907.00904
[80] Yuan Y, Pan J, Wang X, Fang Y, Song C, Wang L, He K, Ma X, Zhang H, Huang F, Li W, Xue Q K 2019 Nat. Phys. 15 1046
[81] Jiang K, Dai X, Wang Z 2019 Phys. Rev. X 9 011033
[82] Yin J X, Wu Z, Wang J H, Ye Z Y, Gong J, Hou X Y, Shan L, Li A, Liang X J, Wu X X, Li J, Ting C S, Wang Z Q, Hu J P, Hor P H, Ding H, Pan S H 2015 Nat. Phys. 11 543
计量
- 文章访问数: 13510
- PDF下载量: 691
- 被引次数: 0













 下载:
下载: