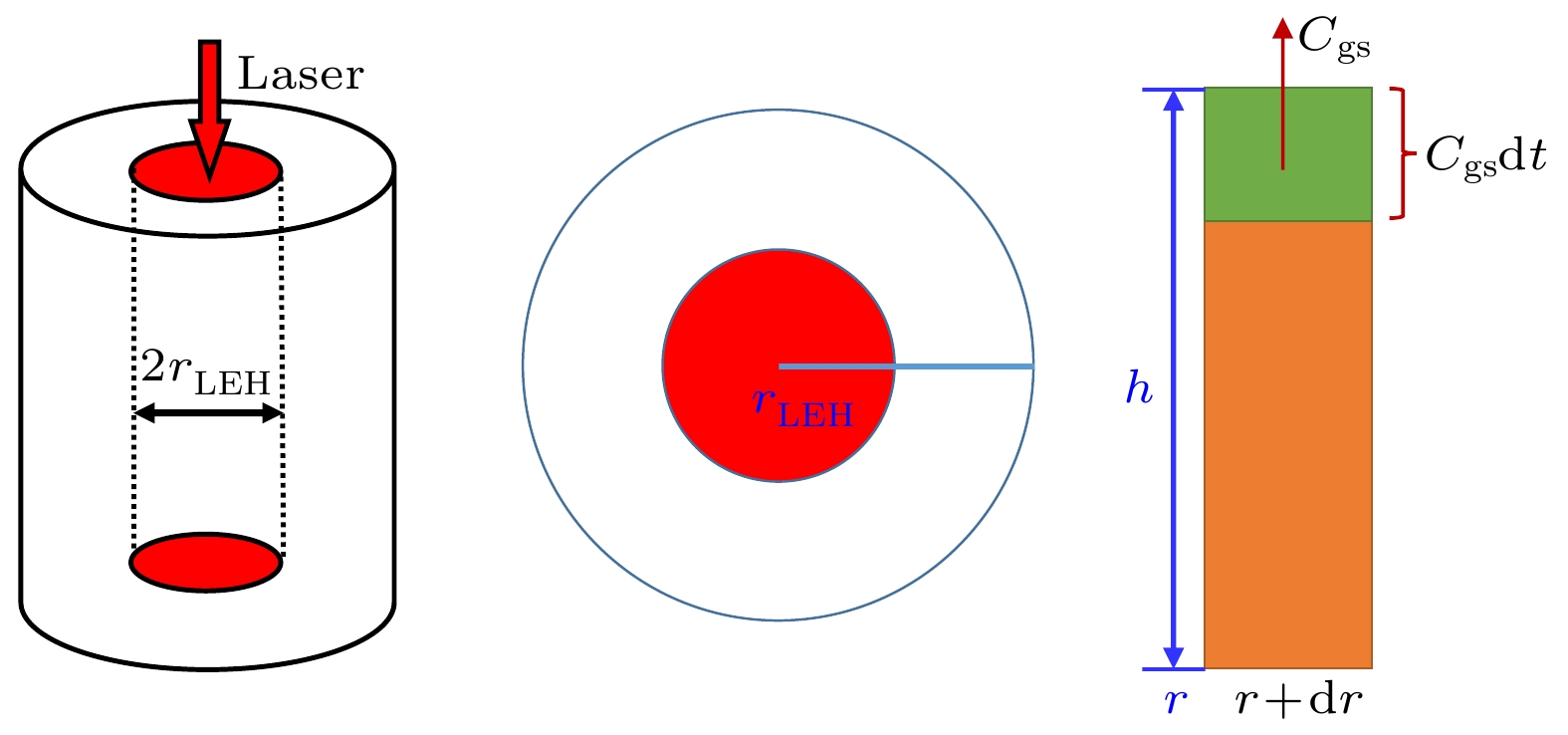
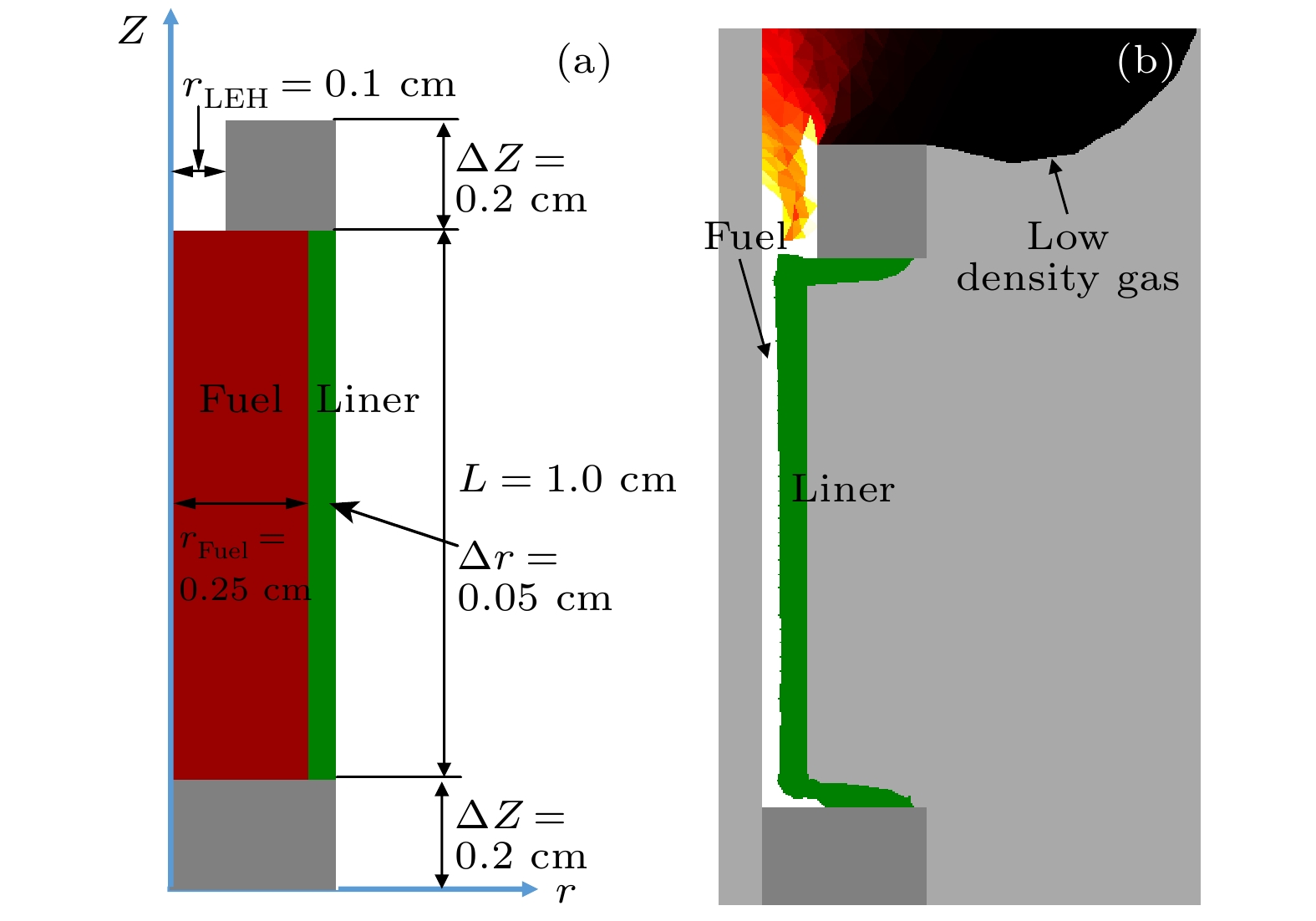
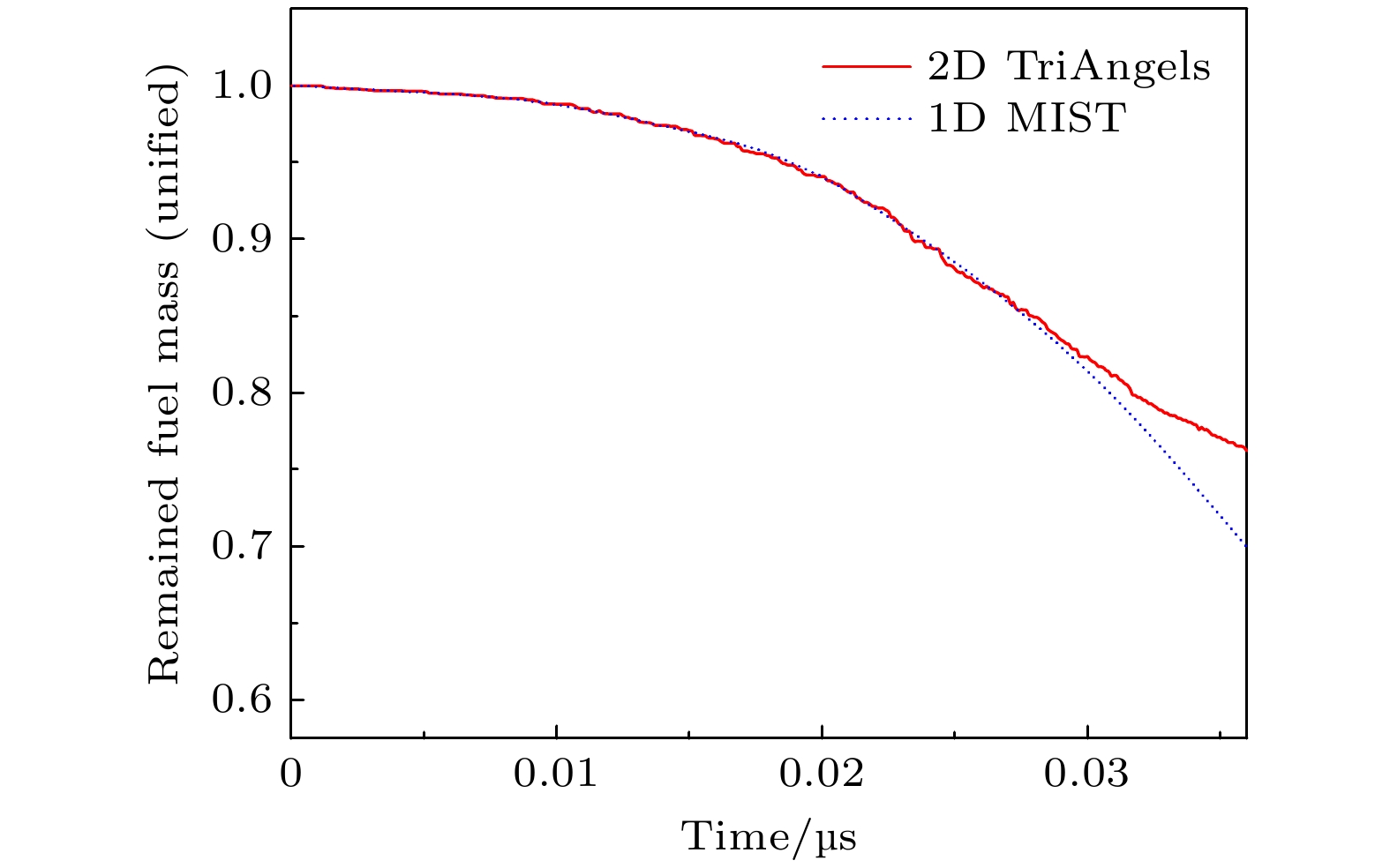
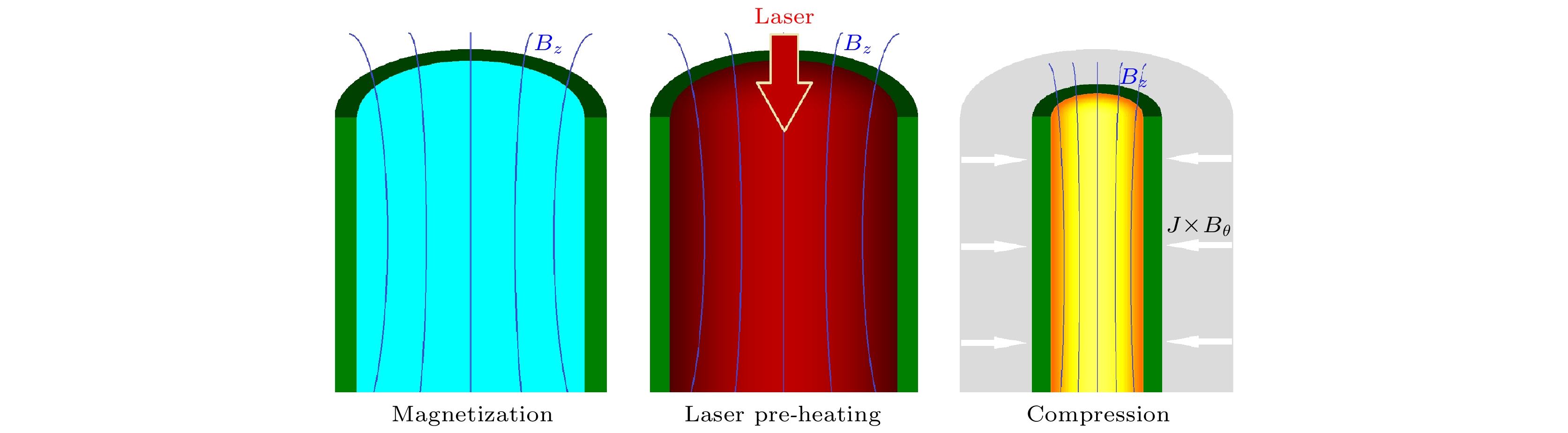
-
得益于激光预加热和轴向磁场的作用, 磁化套筒惯性聚变(magnetized liner inertial fusion, MagLIF)构型理论上能有效降低聚变实现的难度, 具有极大的应用潜力. 本文选择MagLIF过程中伴随激光预加热所必然存在端面损失效应作为研究目标, 搭建了能够描述几何参数与腊肠不稳定性等高维效应的一维唯象物理模型, 并分别通过与二维流体动力学程序和国外同类程序的计算对比完成参数拟合校验; 在此基础上, 获得端面损失效应对MagLIF内爆过程及预加热效果的影响规律. 计算结果表明: 不同喷射半径下MagLIF负载在内爆过程的绝大多数时间内保持了相近的流体动力学演化过程, 并在迟滞阶段经历了相同的质量损失比例, 且考虑端面效应后得到的预加热和内爆产额相对变差, 但却不改变规律性的趋势. 所建立的模型与结论有助于加深对MagLIF预加热和端面损失过程中物理图像的认知和理解.Benefiting from laser preheat and magnetization, magnetized liner lnertial fusion (MagLIF) has a promising potential because theoretically it can dramatically lower the difficulties in realizing the controlled fusion. In this paper, the end loss effect caused by laser preheat in MagLIF process is chosen as an objective to explore its influences, and a one-dimensional and heuristic model of this effect is proposed based on the jet model of ideal fluid, in which the high-dimensional influences, such as geometric parameters and sausage instability, are taken into consideration. To complete the verification progress, the calculation results of one-dimensional MIST code and two-dimensional programs TriAngels and HDYRA are compared, and the application scopes of this heuristic model are discussed and summarized. Based on this model, the key parameters and influences of the end loss effect on the MagLIF implosion process and pre-heating effect are obtained. The calculation results show that the MagLIF load maintains a similar hydrodynamic evolution process in most of the implosion processes with different laser entrance radii, and experiences the same percentage of mass (～16%) lost during stagnation stage. With the same driving current, the fuel temperature will rise higher in the model with more mass losing, so the fusion yields do not change too much. The mass loss ratio seems to play a dominant role. It is recommended to design the laser entrance hole as small as possible in the experiment to increase the yield. The predictions obtained after considering the end loss effect lower the preheating temperature and fusion yield, but no change happens to the regularity trend. As the liner height increases, the preheating temperature, peak current, fuel internal energy, and fusion yield each still show a monotonically downward trend. Therefore, under the premise of fixed driving capability and laser output capability, it is suggested that the liner height in MagLIF load design should be as short as possible. The established heuristic model and conclusions are helpful in better understanding the physical mechanism in the process of MagLIF preheat and end loss.
-
Keywords:
- magnetized liner lnertial fusion /
- end loss effect /
- heuristic model
[1] Ding B J, Bonoli P T, Tuccillo A, Goniche M, Kirov K, Li M, Li Y, Cesario R, Peysson Y, Ekedahl A, Amicucci L, Baek S, Faust I, Parker R, Shiraiwa S, Wallace G M, Cardinali A, Castaldo C, Ceccuzzi S, Mailloux J, Napoli F, Liu F, Wan B 2018 Nucl. Fusion 58 095003
Google Scholar
[2] Makwana K D, Keppens R, Lapenta G 2018 Phys. Plasmas 25 082904
Google Scholar
[3] Shimomura Y, Spears W 2004 IEEE Trans. Plasma Sci. 14 1369
Google Scholar
[4] Clark D S, Weber C R, Milovich J L, Pak A E, Casey D T, Hammel B A, Ho D D, Jones O S, Koning J M, Kritcher A L, Marinak M M, Masse L P, Munro D H, Patel M V, Patel P K, Robey H F, Schroeder C R, Sepke S M, Edwards M J 2019 Phys. Plasmas 26 050601
Google Scholar
[5] Perkins L J, Logan B G, Zimmerman G B, Werner C J 2013 Phys. Plasmas 20 072708
Google Scholar
[6] McCrory R L, Meyerhofer D D, Betti R, Craxton R S, Delettrez J A, Edgell D H, Glebov V Yu, Goncharov V N, Harding D R, Jacobs-Perkins D W, Knauer J P, Marshall F J, McKenty P W, Radha P B, Regan S P 2008 Phys. Plasmas 15 055503
Google Scholar
[7] Chen Y Y, Bao X H, Fu P, Gao G 2019 Chin. Phys. B 28 015201
Google Scholar
[8] Zhang Y K, Zhou R J, Hu L Q, Chen M W, Chao Y 2018 Chin. Phys. B 27 055206
Google Scholar
[9] Tikhonchuk V, Gu Y J, Klimo O, Limpouch J, Weber S 2019 Matter Radiat. Extremes 4 045402
Google Scholar
[10] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 24 094701
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 24 094701
Google Scholar
[11] Wu F Y, Chu Y Y, Ramis R, Li Z H, Ma Y Y, Yang J L, Wang Z, Ye F, Huang Z C, Qi J M, Zhou L, Liang C, Chen S J, Ge Z Y, Yang X H, Wang S W 2018 Matter Radiat. Extremes 3 248
Google Scholar
[12] Ding N, Zhang Y, Xiao D L, Wu J M, Dai Z H, Yin L, Gao Z M, Sun S K, Xue C, Ning C, Shu X J, Wang J G 2016 Matter Radiat. Extremes 1 135
Google Scholar
[13] Slutz S A, Herrmann M C, Vesey R A, Sefkow A B, Sinars D B, Rovang D C, Peterson K J, Cuneo M E 2010 Phys. Plasmas 17 056303
Google Scholar
[14] Paradela J, García-Rubio F, Sanz J 2019 Phys. Plasmas 26 012705
Google Scholar
[15] Slutz S A, Vesey R A 2012 Phys. Rev. Lett 108 025003
Google Scholar
[16] Sefkow A B, Slutz S A, Koning J M, Marinak M M, Peterson K J, Sinars D B, Vesey R A 2014 Phys. Plasmas 21 072711
Google Scholar
[17] Slutz S A 2018 Phys. Plasmas 25 082707
Google Scholar
[18] Gomez M R, Slutz S A, Sefkow A B, Sinars D B, Hahn K, D, Hansen S B, Harding E C, Knapp P F, Schmit P F, Jennings C A, Awe T J, Geissel M, Rovang D C, Chandler G A, Cooper G W, Cuneo M E, Harvey-Thompson A J, Herrmann M C, Hess M H, Johns O, Lamppa D C, Martin M R, McBride R D, Peterson K J, Porter J L, Robertson G K, Rochau G A, Ruiz C L, Savage M E, Smith I C, Stygar W A, Vesey R A 2014 Phys. Rev. Lett 113 155003
Google Scholar
[19] Awe T J, McBride R D, Jennings C A, Lamppa D C, Martin M R, Rovang D C, Slutz S A, Cuneo M E, Owen A C, Sinars D B, Tomlinson K, Gomez M R, Hansen S B, Herrmann M C, McKenney J L, Nakhleh C, Robertson G K, Rochau G A, Savage M E, Schroen D G, Stygar W A 2013 Phys. Rev. Lett 111 235005
Google Scholar
[20] Seyler C E, Martin M R, Hamlin N D 2018 Phys. Plasmas 25 062711
Google Scholar
[21] Geissel M, Harvey-Thompson A J, Awe T J, Bliss D E, Glinsky M E, Gomez M R, Harding E, Hansen S B, Jennings C, Kimmel M W, Knapp P, Lewis S M, Peterson K, Schollmeier M, Schwarz J, Shores J E, Slutz S A, Sinars D B, Smith I C, Speas C S, Vesey R A, Weis M R, Porter J L 2018 Phys. Plasmas 25 022706
Google Scholar
[22] Davies J R, Bahr R E, Barnak D H, Betti R, Bonino M J, Campbell E M, Hansen E C, Harding D R, Peebles J L, Sefkow A B, Seka W, Chang P Y, Geissel M, Harvey-Thompson A J 2018 Phys. Plasmas 25 062704
Google Scholar
[23] Slutz S A 2015 Sandia National Laboratory Report SAND2015-1515R
[24] 赵海龙, 肖波, 王刚华, 王强, 章征伟, 孙奇志, 邓建军 2020 69 035203
Google Scholar
Zhao H L, Xiao B, Wang G H, Wang Q, Zhang Z W, Sun Q Z, Deng J J 2020 Acta Phys. Sin. 69 035203
Google Scholar
[25] 赵海波, 肖波, 柏劲松, 段书超, 王刚华, 阚明先, 陈芳 2018 高压 32 042303
Google Scholar
Zhao H B, Xiao B, Bai J S, Duan S C, Wang G H, Kan M X, Chen F 2018 Chin. J. High Pressure Phys. 32 042303
Google Scholar
[26] 赵海波 2018 硕士学位论文 (北京: 中国工程物理研究院研究生部)
Zhao H B 2018 M. S. Thesis (Beijing: China Academy of Engineering Physics) (in Chinese)
[27] Jennings C A, Chittenden J P, Cuneo M E, Stygar W A, Ampleford D J, Waisman E M, Jones M, Savage M E, LeChien K R, Wagoner T C 2010 IEEE Trans. Plasma Sci. 38 529
Google Scholar
[28] McBride R D, Jennings C A, Vesey R A, Rochau G A, Savage M E, Stygar W A, Cuneo M E, Sinars D B, Jones M, LeChien K R, Lopez M R, Moore J K, Struve K W, Wagoner T C, Waisman E M 2010 Phys. Rev. ST Accel. Beams 13 120401
Google Scholar
-
图 1 MagLIF过程示意图(包含3个主要阶段)
Fig. 1. Schematic of MagLIF process, including three main stages.
图 3 由轴向压力不平衡引发的腊肠不稳定性种子示意图
Fig. 3. Schematic of instability seed caused by axial pressure imbalance.
图 4 标准流体动力学模型 (a) 初始负载参数; (b) 36 ns时密度分布示意图
Fig. 4. (a) Initial parameters and (b) density distribution at 36 ns calculated by TriAngels.
图 5 MIST与TriAngels计算得到的套筒内剩余燃料质量随时间演化关系
Fig. 5. Comparison between remained fuel mass calculated by MIST and TriAngels.
图 6 不同初始条件影响下MIST与TriAngels计算得到的套筒内剩余燃料质量随时间演化关系(A = 0.31) (a) h = 0.75 cm; (b) g = 2 mg/cm3; (c) rLEH = 0.15 cm
Fig. 6. Comparison between remained fuel mass calculated by MIST and TriAngels under different initial parameters (A = 0.31): (a) h = 0.75 cm; (b) g = 2 mg/cm3; (c) rLEH = 0.15 cm.
图 7 MIST计算所使用的(a)驱动电流曲线, 以及(b)剩余燃料质量随时间演化曲线
Fig. 7. Demonstrations of (a) driving current and (b) remained fuel mass calculated by MIST.
图 8 MIST计算得到的剩余燃料质量随时间演化曲线(B = 0.42, ρ = 2.0 mg/cm3)
Fig. 8. Remained fuel mass evolving with time calculated by MIST (B = 0.42, ρ = 2.0 mg/cm3).
图 9 不同LEH半径下MIST计算得到的(a)聚变产额和(b) 余燃料比例随时间演化曲线
Fig. 9. (a) Fusion yield and (b) remained fuel mass calculated by MIST under different LEH radii.
图 10 不同LEH半径下, MIST计算得到的139 ns时的 (a)密度分布和(b)温度分布
Fig. 10. Distributions of (a) density and (b) temperature calculated by MIST under different LEH radii at 139 ns.
图 11 不同LEH半径下MIST计算得到的(a)交界面演化曲线和(b)迟滞时刻温度分布图
Fig. 11. (a) Liner-fuel interface evolving with time and (b) temperature distribution at stagnation time calculated by MIST under different LEH radii.
图 13 MIST计算使用的(a)绝缘堆电压曲线和(b)负载电流曲线
Fig. 13. (a) Voltage curve from the vacuum insulator and (b) load current curve calculated by MIST code.
表 1 不同套筒高度计算得到的内爆结果对比(不考虑端面损失效应)
Table 1. Calculated implosion results at different liner heights by MIST (without end loss effect)
套筒高度h/cm 预加热温度/eV 峰值电流/MA 燃料峰值内能/(kJ·cm–1) 聚变产额/(kJ·cm–1) 能量增益Q 0.50 890 29.5 786 2426 3.1 0.75 615 28.9 668 2133 3.2 1.00 450 28.2 565 1614 2.9 1.25 364 27.4 478 1172 2.5 
下载: 导出CSV
表 2 不同套筒高度计算得到的内爆结果对比(考虑端面损失效应)
Table 2. Calculated implosion results at different liner heights by MIST (with end loss effect).
套筒高度h/cm 预加热温度/eV 峰值电流/MA 燃料峰值内能/(kJ·cm–1) 聚变产额/(kJ·cm–1) 能量增益Q 0.50 890 29.5 486 1850 3.8 0.75 615 28.9 480 1660 3.45 1.00 450 28.2 440 1320 3.0 1.25 364 27.4 400 990 2.48
下载: 导出CSV
-
[1] Ding B J, Bonoli P T, Tuccillo A, Goniche M, Kirov K, Li M, Li Y, Cesario R, Peysson Y, Ekedahl A, Amicucci L, Baek S, Faust I, Parker R, Shiraiwa S, Wallace G M, Cardinali A, Castaldo C, Ceccuzzi S, Mailloux J, Napoli F, Liu F, Wan B 2018 Nucl. Fusion 58 095003
Google Scholar
[2] Makwana K D, Keppens R, Lapenta G 2018 Phys. Plasmas 25 082904
Google Scholar
[3] Shimomura Y, Spears W 2004 IEEE Trans. Plasma Sci. 14 1369
Google Scholar
[4] Clark D S, Weber C R, Milovich J L, Pak A E, Casey D T, Hammel B A, Ho D D, Jones O S, Koning J M, Kritcher A L, Marinak M M, Masse L P, Munro D H, Patel M V, Patel P K, Robey H F, Schroeder C R, Sepke S M, Edwards M J 2019 Phys. Plasmas 26 050601
Google Scholar
[5] Perkins L J, Logan B G, Zimmerman G B, Werner C J 2013 Phys. Plasmas 20 072708
Google Scholar
[6] McCrory R L, Meyerhofer D D, Betti R, Craxton R S, Delettrez J A, Edgell D H, Glebov V Yu, Goncharov V N, Harding D R, Jacobs-Perkins D W, Knauer J P, Marshall F J, McKenty P W, Radha P B, Regan S P 2008 Phys. Plasmas 15 055503
Google Scholar
[7] Chen Y Y, Bao X H, Fu P, Gao G 2019 Chin. Phys. B 28 015201
Google Scholar
[8] Zhang Y K, Zhou R J, Hu L Q, Chen M W, Chao Y 2018 Chin. Phys. B 27 055206
Google Scholar
[9] Tikhonchuk V, Gu Y J, Klimo O, Limpouch J, Weber S 2019 Matter Radiat. Extremes 4 045402
Google Scholar
[10] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 24 094701
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 24 094701
Google Scholar
[11] Wu F Y, Chu Y Y, Ramis R, Li Z H, Ma Y Y, Yang J L, Wang Z, Ye F, Huang Z C, Qi J M, Zhou L, Liang C, Chen S J, Ge Z Y, Yang X H, Wang S W 2018 Matter Radiat. Extremes 3 248
Google Scholar
[12] Ding N, Zhang Y, Xiao D L, Wu J M, Dai Z H, Yin L, Gao Z M, Sun S K, Xue C, Ning C, Shu X J, Wang J G 2016 Matter Radiat. Extremes 1 135
Google Scholar
[13] Slutz S A, Herrmann M C, Vesey R A, Sefkow A B, Sinars D B, Rovang D C, Peterson K J, Cuneo M E 2010 Phys. Plasmas 17 056303
Google Scholar
[14] Paradela J, García-Rubio F, Sanz J 2019 Phys. Plasmas 26 012705
Google Scholar
[15] Slutz S A, Vesey R A 2012 Phys. Rev. Lett 108 025003
Google Scholar
[16] Sefkow A B, Slutz S A, Koning J M, Marinak M M, Peterson K J, Sinars D B, Vesey R A 2014 Phys. Plasmas 21 072711
Google Scholar
[17] Slutz S A 2018 Phys. Plasmas 25 082707
Google Scholar
[18] Gomez M R, Slutz S A, Sefkow A B, Sinars D B, Hahn K, D, Hansen S B, Harding E C, Knapp P F, Schmit P F, Jennings C A, Awe T J, Geissel M, Rovang D C, Chandler G A, Cooper G W, Cuneo M E, Harvey-Thompson A J, Herrmann M C, Hess M H, Johns O, Lamppa D C, Martin M R, McBride R D, Peterson K J, Porter J L, Robertson G K, Rochau G A, Ruiz C L, Savage M E, Smith I C, Stygar W A, Vesey R A 2014 Phys. Rev. Lett 113 155003
Google Scholar
[19] Awe T J, McBride R D, Jennings C A, Lamppa D C, Martin M R, Rovang D C, Slutz S A, Cuneo M E, Owen A C, Sinars D B, Tomlinson K, Gomez M R, Hansen S B, Herrmann M C, McKenney J L, Nakhleh C, Robertson G K, Rochau G A, Savage M E, Schroen D G, Stygar W A 2013 Phys. Rev. Lett 111 235005
Google Scholar
[20] Seyler C E, Martin M R, Hamlin N D 2018 Phys. Plasmas 25 062711
Google Scholar
[21] Geissel M, Harvey-Thompson A J, Awe T J, Bliss D E, Glinsky M E, Gomez M R, Harding E, Hansen S B, Jennings C, Kimmel M W, Knapp P, Lewis S M, Peterson K, Schollmeier M, Schwarz J, Shores J E, Slutz S A, Sinars D B, Smith I C, Speas C S, Vesey R A, Weis M R, Porter J L 2018 Phys. Plasmas 25 022706
Google Scholar
[22] Davies J R, Bahr R E, Barnak D H, Betti R, Bonino M J, Campbell E M, Hansen E C, Harding D R, Peebles J L, Sefkow A B, Seka W, Chang P Y, Geissel M, Harvey-Thompson A J 2018 Phys. Plasmas 25 062704
Google Scholar
[23] Slutz S A 2015 Sandia National Laboratory Report SAND2015-1515R
[24] 赵海龙, 肖波, 王刚华, 王强, 章征伟, 孙奇志, 邓建军 2020 69 035203
Google Scholar
Zhao H L, Xiao B, Wang G H, Wang Q, Zhang Z W, Sun Q Z, Deng J J 2020 Acta Phys. Sin. 69 035203
Google Scholar
[25] 赵海波, 肖波, 柏劲松, 段书超, 王刚华, 阚明先, 陈芳 2018 高压 32 042303
Google Scholar
Zhao H B, Xiao B, Bai J S, Duan S C, Wang G H, Kan M X, Chen F 2018 Chin. J. High Pressure Phys. 32 042303
Google Scholar
[26] 赵海波 2018 硕士学位论文 (北京: 中国工程物理研究院研究生部)
Zhao H B 2018 M. S. Thesis (Beijing: China Academy of Engineering Physics) (in Chinese)
[27] Jennings C A, Chittenden J P, Cuneo M E, Stygar W A, Ampleford D J, Waisman E M, Jones M, Savage M E, LeChien K R, Wagoner T C 2010 IEEE Trans. Plasma Sci. 38 529
Google Scholar
[28] McBride R D, Jennings C A, Vesey R A, Rochau G A, Savage M E, Stygar W A, Cuneo M E, Sinars D B, Jones M, LeChien K R, Lopez M R, Moore J K, Struve K W, Wagoner T C, Waisman E M 2010 Phys. Rev. ST Accel. Beams 13 120401
Google Scholar
下载:
计量
- 文章访问数: 4064
- PDF下载量: 44
- 被引次数: 0
