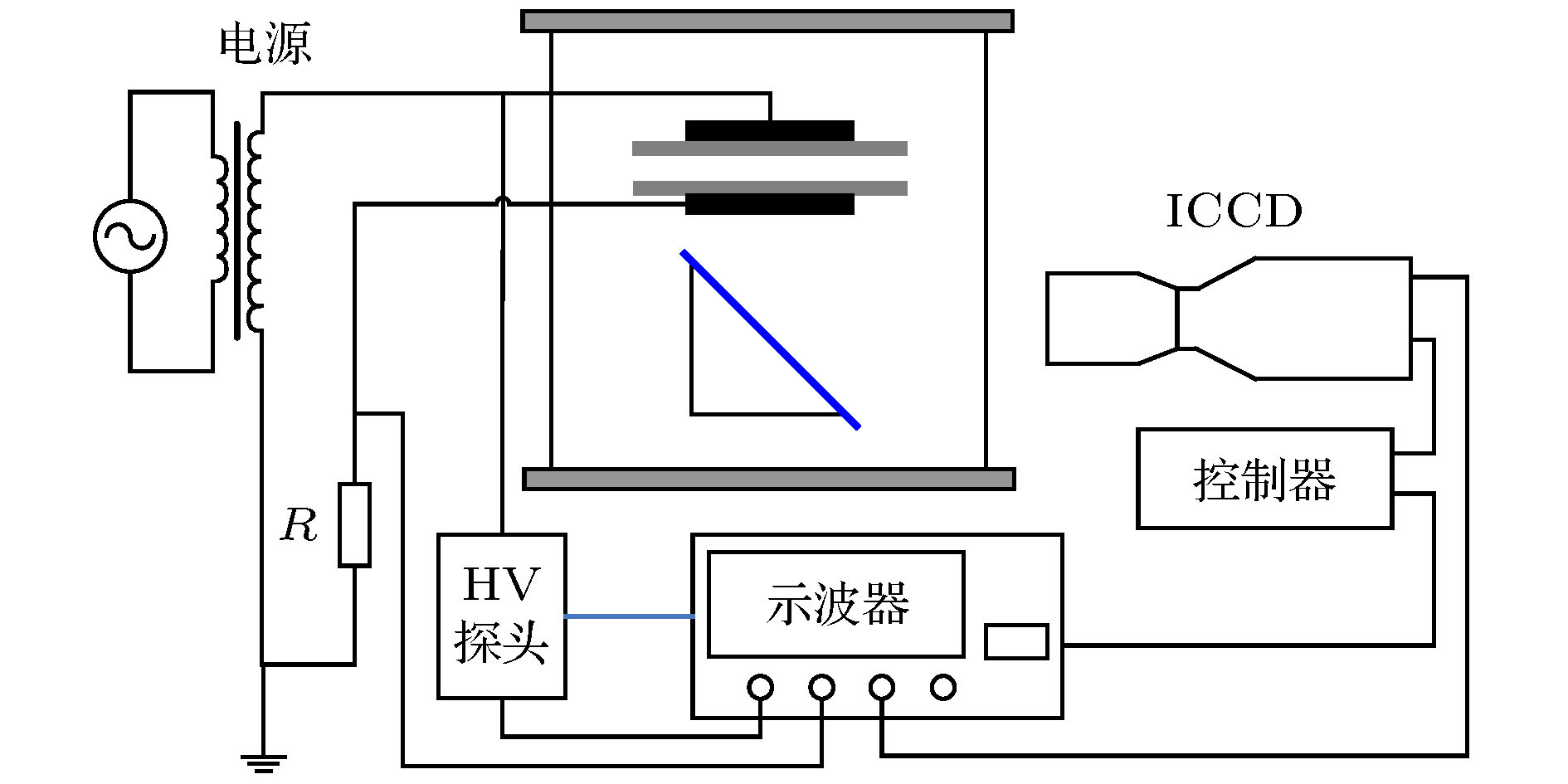
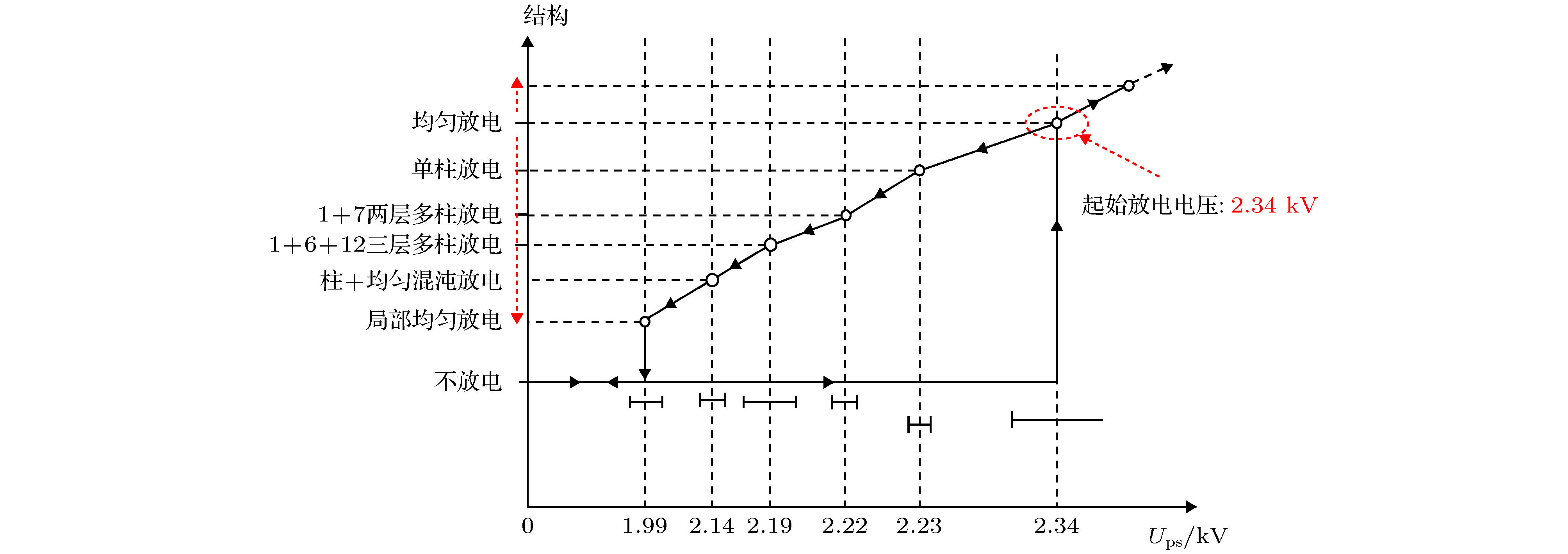
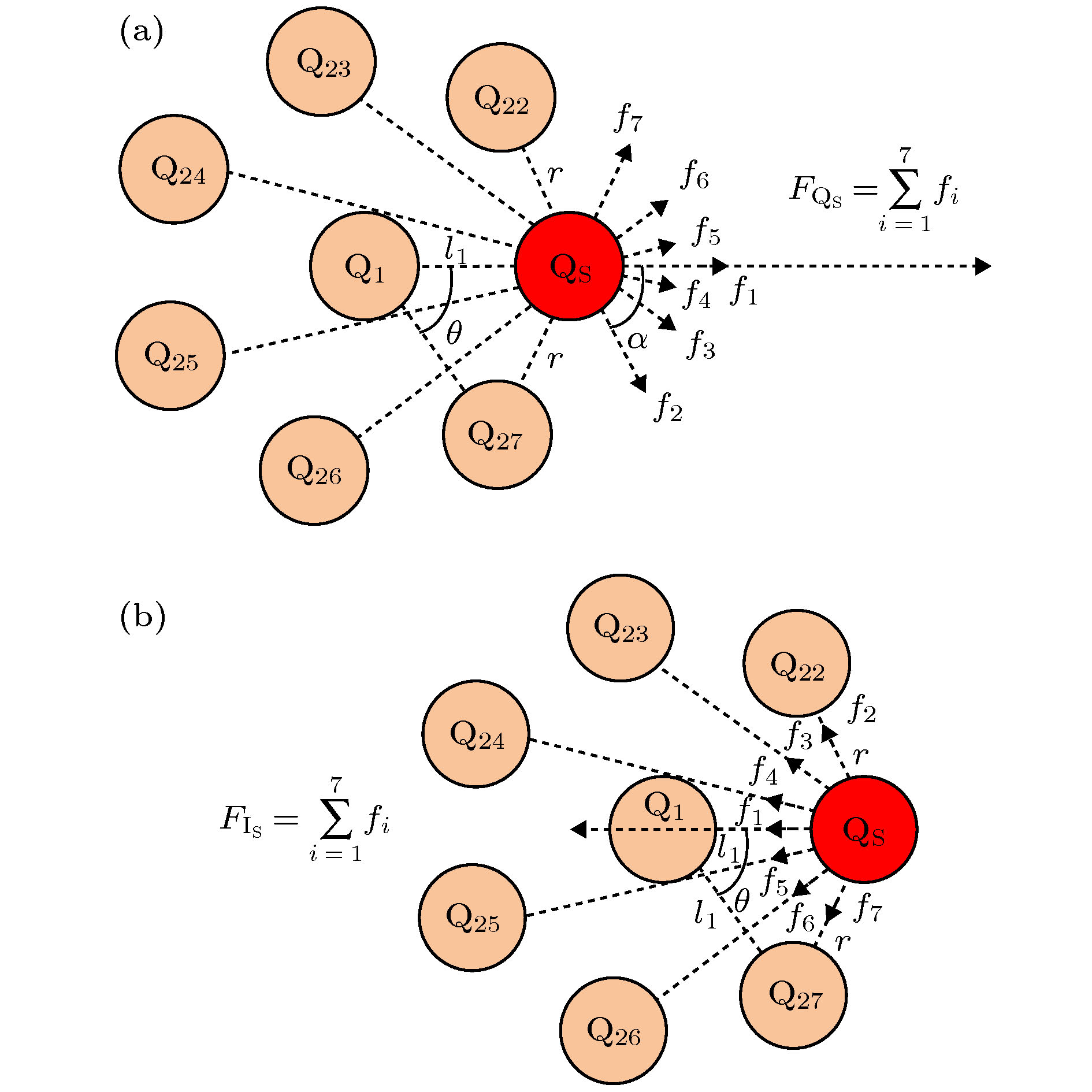
-
介质阻挡放电被众多工业领域用作低温等离子体源, 柱状放电是介质阻挡放电的重要形式之一, 但其放电理论尚未掌握. 进行大气压氦气介质阻挡放电实验, 通过降低外施电压低于起始放电电压实现了柱状放电从单柱到多柱的斑图演化, 拍摄了电极底面放电图像, 测量了外施电压、放电电流、放电转移电荷、放电柱的柱直径和柱间距, 计算了放电柱受其他所有柱施加的库仑力与磁场力. 结果表明: 外施电压变化瞬间电极底面放电图像呈现出动态演化过程. 不同层放电柱的柱直径由中心向外层依次增大. 计算发现演化稳定后放电柱所受库仑力远大于磁场力, 推理存在一约束势平衡库仑力使放电柱稳定分布. 不同电压、位置的放电柱所受库仑力不同: 不同层的放电柱所受库仑力由最外层至中心柱依次减小, 中心柱受力为0, 最外层放电柱的约束势应最大而中心放电柱的约束势应该最小; 外施电压降低, 介质表面电荷和放电柱总数的共同作用导致库仑力增大, 约束势也应有所增大, 即约束势受介质表面电荷、放电柱总数与位置的共同影响.Dielectric barrier discharge is widely used as a low-temperature plasma source in industry. Columnar discharge is an important form of dielectric barrier discharge. However, its discharge theory has not been clear yet. In this paper, the dielectric barrier discharges in helium at atmospheric pressure are carried out between parallel dielectric barrier electrodes to study the evolutionary dynamics of single-multiple columns. By reducing the applied voltages to a value lower than the initial discharge voltage, the pattern of the columnar discharge evolves from a single column into multiple columns. Discharge images from the bottom are taken to observe the evolution of discharge and measure the diameter of discharge column and spacing between columns. The applied voltage, the Lissajous figure, the discharge current, and the discharge transferred charge are measured in order to calculate the Coulomb force and the magnetic field force exerted on the column by the other columns. It is found that in columnar discharge, there is a dynamic evolution process that the single columnar discharge evolves into the two-layered columnar discharge when the applied voltage slightly decreases instantaneously. On the one hand, the column diameter is different in different layer: the column diameter increases from the center to the outer layer. On the other hand, as the applied voltage decreases, the diameter of the center column grows and the spacing between the center column and its adjacent column decreases. The calculations show that the Coulomb force is far greater than the magnetic field force when the evolution is stable, which indicates that, as mentioned in the established knowledge, there is a confinement potential to balance the Coulomb force, thereby keeping the distribution of discharge columns stable. Furthermore, the results also show that the Coulomb force on the discharge columns at different voltage and position is different. The strength of Coulomb force on column is different at different layer: it decreases from the outermost layer to the center column, which is zero on the center column. Based on the balance between the Coulomb force and the confinement potential in columnar discharge, it is suggested that the strength of the latter may also follow the same law. In addition, as the applied voltage decreases, the charges accumulated on the surface of the dielectric and the number of discharge columns both increase, which results in the increase of the maximum of the Coulomb force. The confinement potential may increase as well and follow the same law.
-
Keywords:
- columnar pattern discharge /
- spatio-temporal evolution /
- coulomb force /
- confinement potential
[1] 王新新 2009 高电压技术 35 1
Google Scholar
Wang X X 2009 High Volt. Eng. 35 1
Google Scholar
[2] 郝艳捧, 关志成, 王黎明, 王新新, 李成榕 2005 高电压技术 31 42
Google Scholar
Hao Y P, Guan Z C, Wang L M, Wang X X, Li C R 2005 High Volt. Eng. 31 42
Google Scholar
[3] Ding H X, Zhu A M, Lu F G, Xu Y, Zhang J, Yang X F 2006 J. Phys. D: Appl. Phys. 39 3603
Google Scholar
[4] Durme J V, Dewulf J, Leys C, Langenhove H V 2008 Appl. Catal. B: Environ. 78 324
Google Scholar
[5] Kim H H 2004 Plasma Process Polym. 1 91
Google Scholar
[6] Kogelschatz U 2002 IEEE Trans. Plasma Sci. 30 1400
Google Scholar
[7] Golubovskii Y B, Maiorov V A, Behnke J, Behnke J F 2003 J. Phys. D: Appl. Phys. 36 39
Google Scholar
[8] Luo H Y, Liang Z, Wang X X, Guan Z C, Wang L M 2010 J. Phys. D: Appl. Phys. 43 155201
Google Scholar
[9] Astrov Y A, Logvin Y A 1997 Phys. Rev. Lett. 79 2983
Google Scholar
[10] Dong L F, Shang J, He Y F, Bai Z G, Liu L, Fan W L 2012 Phys. Rev. E 85 066403
Google Scholar
[11] 梁卓, 罗海云, 王新新, 关志成, 王黎明 2010 59 8739
Google Scholar
Liang Z, Luo H Y, Wang X X, Guan Z C, Wang L M 2010 Acta Phys. Sin. 59 8739
Google Scholar
[12] Mukaigawa S, Fujiwara K, Sato T, Odagiri R, Kudoh T, Yokota A, Oguni K, Takaki K 2016 Jpn. J. Appl. Phys. 55 07LB04
Google Scholar
[13] Hao Y P, Han Y Y, Huang Z M, Yang L, Dai D, Li L C 2018 Phys. Plasmas 25 013516
Google Scholar
[14] Radu I, Bartnikas R, Czeremuszkin G, Wertheimer M R 2003 IEEE Trans. Plasma Sci. 31 411
Google Scholar
[15] Astrov Y A, Ammelt E, Purwins H-G 1997 Phys. Rev. Lett. 78 3129
Google Scholar
[16] 董丽芳, 高瑞玲, 贺亚峰, 范伟丽, 李雪辰, 刘书华, 刘微粒 2007 56 1471
Google Scholar
Dong L F, Gao R L, He Y F, Fan W L, Li X C, Liu S H, Liu W L 2007 Acta Phys. Sin. 56 1471
Google Scholar
[17] Hao Y P, Zheng B, Liu Y G 2014 Phys. Plasmas 21 013503
Google Scholar
[18] Müller I, Ammelt E, Purwins H-G 1999 Phys. Rev. Lett. 82 3428
Google Scholar
[19] Hao Y P, Fang Q, Wan H R, Han Y Y, Yang L, Li L C 2019 Phys. Plasmas 26 073518
Google Scholar
[20] Shirafuji T, Kitagawa T, Wakai T, Tachibana K 2003 Appl. Phys. Lett. 83 2309
Google Scholar
[21] Bedanov V M, Peeters F M 1994 Phys. Rev. B 49 2667
Google Scholar
[22] Boeuf J P, Bernecker B, Callegari T, Blanco S, Fournier R 2012 Appl. Phys. Lett. 100 244108
Google Scholar
[23] 郝艳捧, 刘耀阁, 郑彬 2012 高电压技术 38 1025
Google Scholar
Hao Y P, Liu Y G, Zheng B 2012 High Volt. Eng. 38 1025
Google Scholar
[24] 郝艳捧, 阳林, 涂恩来, 陈建阳 2009 高电压技术 35 1879
Google Scholar
Hao Y P, Yang L, Tu E L, Chen J Y 2009 High Volt. Eng. 35 1879
Google Scholar
[25] Falkenstein Z, Coogan J J 1997 J. Phys. D: Appl. Phys. 30 817
Google Scholar
-
图 1 DBD等效电路 (a)未放电阶段; (b)放电阶段
Fig. 1. The simplified electrical equivalent circuit: (a) Non-discharge; (b) discharges.
图 2 大气压DBD实验装置示意图
Fig. 2. Schematic diagram of experimental set-up for DBDs at atmospheric pressure.
图 4 不同外施电压下电极底面放电图像 (a) 2.34 kV; (b) 2.23 kV; (c) 2.22 kV; (d) 2.19 kV; (e) 2.14 kV; (f) 1.99 kV
Fig. 4. End-view discharge images under different Ups: (a) 2.34 kV; (b) 2.23 kV; (c) 2.22 kV; (d) 2.19 kV; (e) 2.14 kV; (f) 1.99 kV.
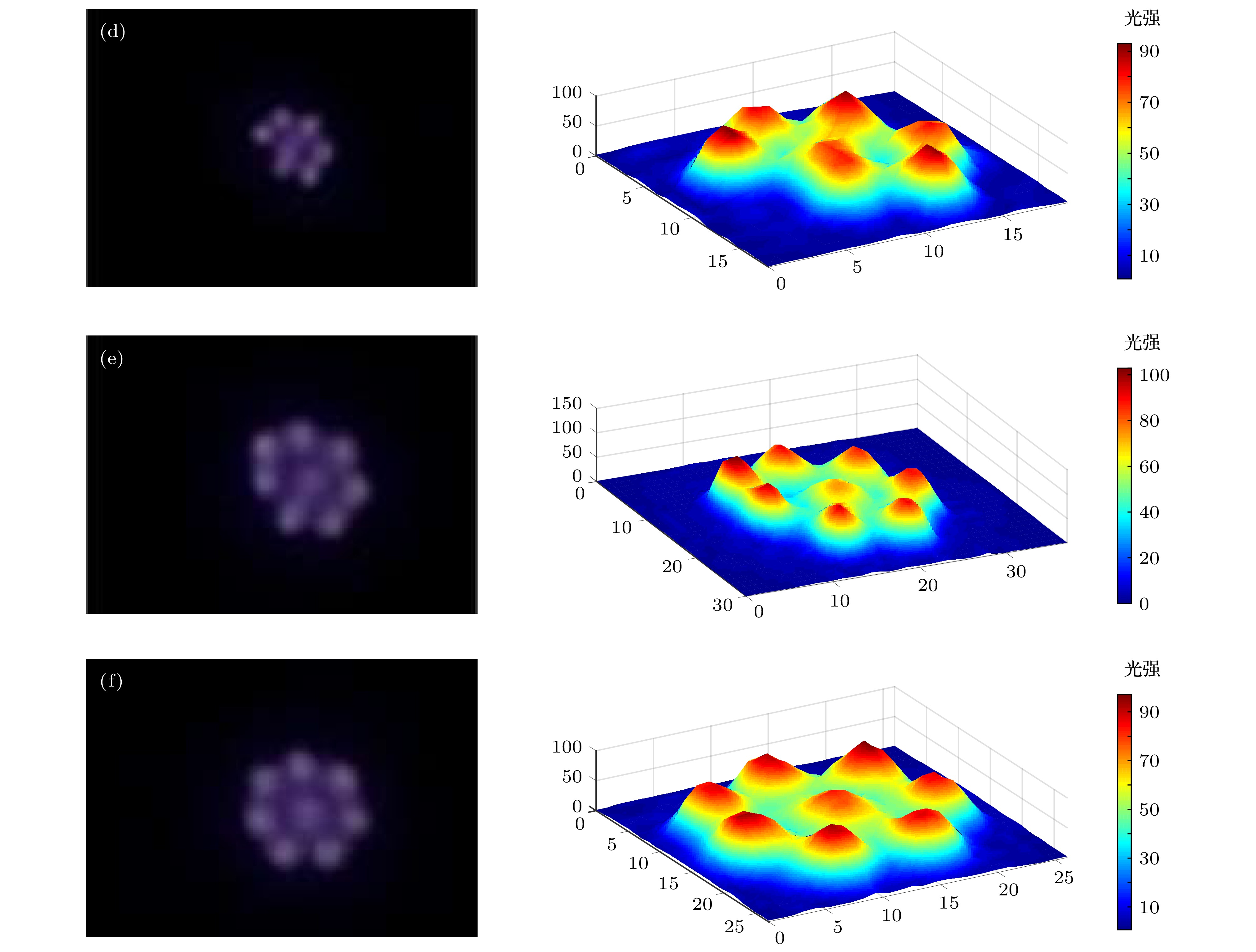
图 5-2 外施电压峰值由2.23 kV降至2.22 kV过程中放电形式的径向演化与光强分布 (a) t = 0, Ups = 2.23 kV → 2.22 kV; (b) t = 0.017 s; (c) t = 0.033 s; (d) t = 0.050 s; (e) t = 0.067 s; (f) t = 0.083 s
Fig. 5-2. Radial evolution of discharge pattern when Ups reduce from 2.23 kV to 2.22 kV: (a) t = 0, Ups = 2.23 kV → 2.22 kV; (b) t = 0.017 s; (c) t = 0.033 s; (d) t = 0.050 s; (e) t = 0.067 s; (f) t = 0.083 s.
图 6 1 + 7两层多柱放电中外层放电柱受力分析 (a)库仑力; (b)磁场力
Fig. 6. Force analysis diagram of discharge column of two layers distribution: (a) Coulomb force; (b) magnetic field force.
图 7 1 + 6 + 12三层多柱放电中三类放电柱的库仑力分析 (a) QS; (b) QS1; (c) QS2
Fig. 7. Coulomb force analysis diagram of discharge column of 3 layers hexagon distribution: (a) QS; (b) QS1; (c) QS2.
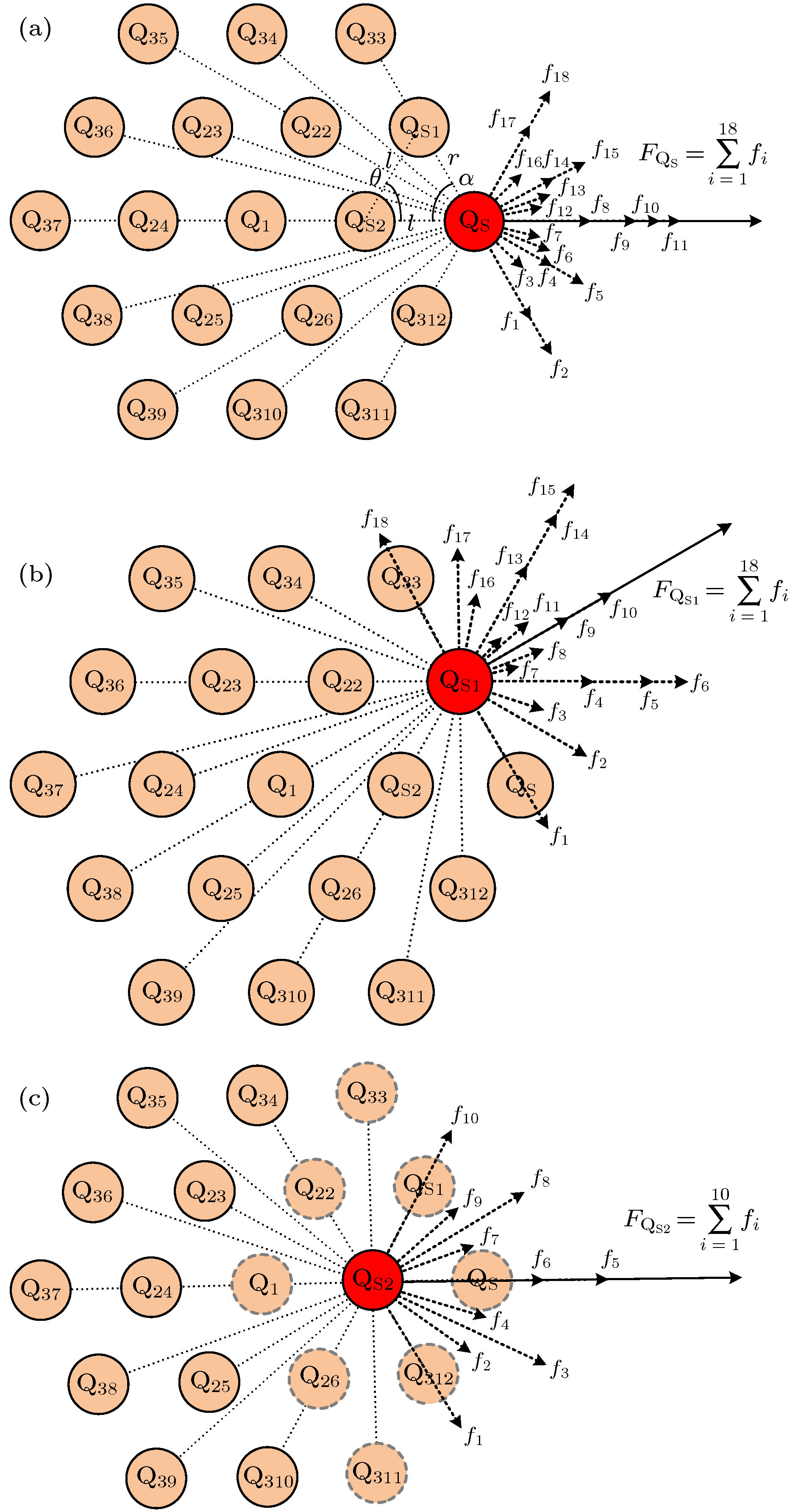
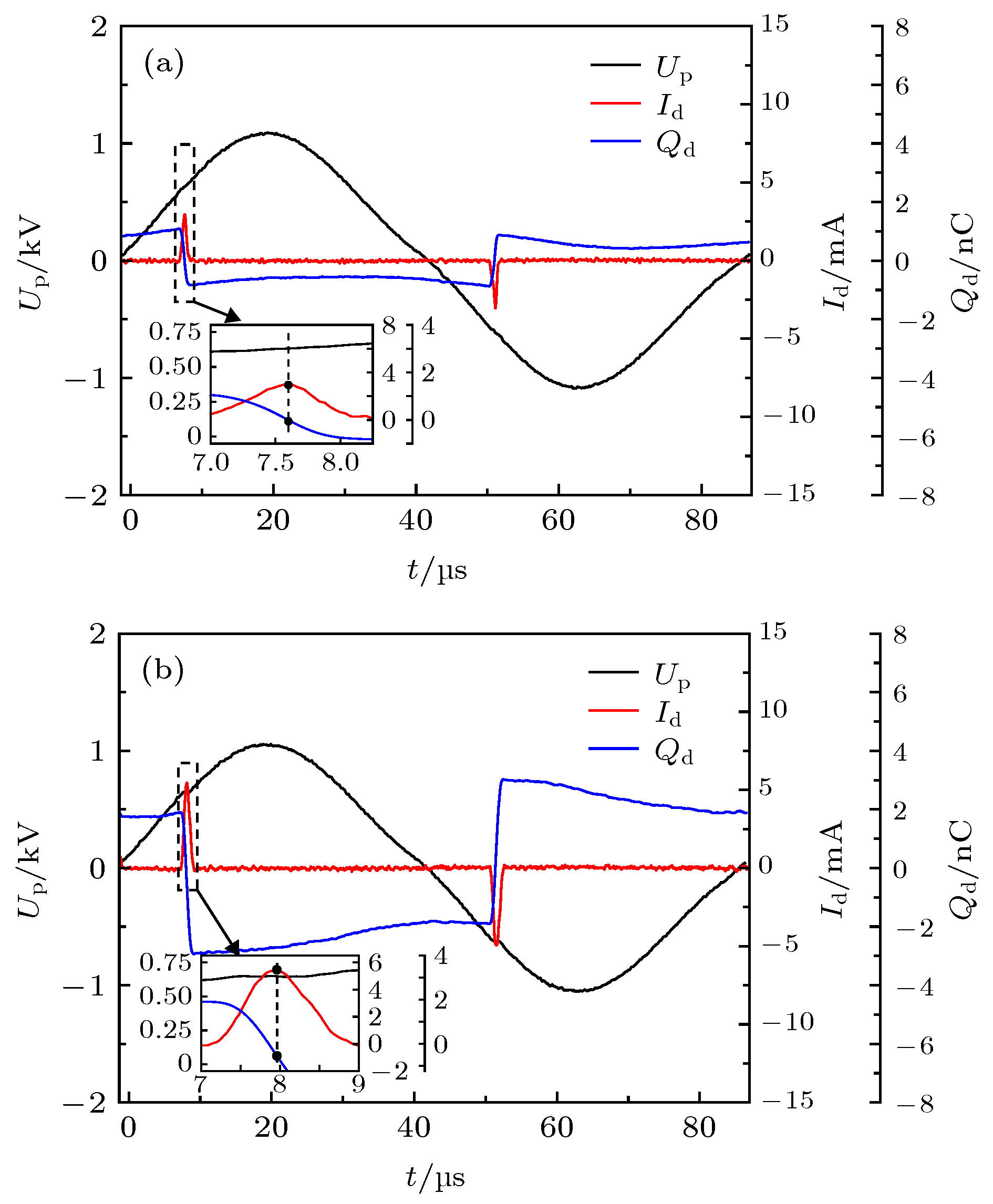
图 8 1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)外施电压、放电电流、放电转移电荷波形(a) 2.22 kV; (b) 2.19 kV. 内插图为电流脉冲时期各波形的局部放大图
Fig. 8. Waves of applied voltage, discharge current and discharge transferred charge: (a) Two layers columnar discharge (2.22 kV); (b) three layers columnar discharge (2.19 kV). The inserted figure is a partial enlarged view of these waveforms during the current pulse period in both (a) and (b).
表 1 单柱放电(2.23 kV)、1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的柱直径、柱间距
Table 1. Diameters and spacing of discharge columns in single-column discharge (2.23 kV), two layers columnar discharge (2.22 kV), and three layers columnar discharge (2.19 kV).
Ups = 2.23 kV Ups = 2.22 kV Ups = 2.19 kV n d1n/mm d1n/mm d2n/mm l12n/mm d1n/mm d2n/mm l12n/mm d3n/mm l23n/mm 1 2.21 3.10 3.59 4.33 3.21 3.42 4.21 3.69 4.03 2 — — 3.50 4.28 — 3.31 3.88 3.43 4.54 3 — — 3.29 4.29 — 3.36 4.25 3.65 3.83 4 — — 3.36 4.55 — 3.45 4.18 3.57 4.47 5 — — 3.37 4.25 — 3.58 4.26 3.59 3.83 6 — — 3.65 4.22 — 3.40 4.14 3.58 4.44 7 — — 3.45 4.26 — — — 3.59 3.85 8 — — — — — — — 3.83 4.38 9 — — — — — — — 3.81 4.01 10 — — — — — — — 3.42 4.27 11 — — — — — — — 3.41 4.05 12 — — — — — — — 3.69 4.30 AVE 2.21 3.10 3.45 4.31 3.21 3.42 4.15 3.61 4.17 D 0 0 1.69% 1.22% 0 0.85% 1.99% 1.94% 6.94% 
下载: 导出CSV
表 2 1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的放电柱受力分析参数
Table 2. Parameters used when calculating Lorentz force and Coulomb force under two layers columnar discharge (2.22 kV) and three layers columnar discharge (2.19 kV).
Ups/kV θ/(°) α/(°) r/mm l/mm h/mm 用于计算FQ 用于计算FI Qd/nC Q/nC Id/mA I/mA 2.22 51.43 64.29 3.74 4.31 3 0.12 0.015 2.95 0.37 2.19 60 60 4.16 4.16 3 0.31 0.016 5.40 0.28
下载: 导出CSV
表 3 1 + 7两层多柱放电(2.22 kV)、1 + 6 + 12三层多柱放电(2.19 kV)的柱间库仑力与磁场力
Table 3. Coulomb force and Lorentz force of discharge columns under two layers columnar discharge (2.22 kV) and three layers columnar discharge (2.19 kV).
Ups/kV FQ/10–7 N FI/10–14 N 2.22 4.01 7.01 2.19 QS QS1 QS2 QS QS1 QS2 5.35 4.82 2.25 4.69 4.22 1.97
下载: 导出CSV
-
[1] 王新新 2009 高电压技术 35 1
Google Scholar
Wang X X 2009 High Volt. Eng. 35 1
Google Scholar
[2] 郝艳捧, 关志成, 王黎明, 王新新, 李成榕 2005 高电压技术 31 42
Google Scholar
Hao Y P, Guan Z C, Wang L M, Wang X X, Li C R 2005 High Volt. Eng. 31 42
Google Scholar
[3] Ding H X, Zhu A M, Lu F G, Xu Y, Zhang J, Yang X F 2006 J. Phys. D: Appl. Phys. 39 3603
Google Scholar
[4] Durme J V, Dewulf J, Leys C, Langenhove H V 2008 Appl. Catal. B: Environ. 78 324
Google Scholar
[5] Kim H H 2004 Plasma Process Polym. 1 91
Google Scholar
[6] Kogelschatz U 2002 IEEE Trans. Plasma Sci. 30 1400
Google Scholar
[7] Golubovskii Y B, Maiorov V A, Behnke J, Behnke J F 2003 J. Phys. D: Appl. Phys. 36 39
Google Scholar
[8] Luo H Y, Liang Z, Wang X X, Guan Z C, Wang L M 2010 J. Phys. D: Appl. Phys. 43 155201
Google Scholar
[9] Astrov Y A, Logvin Y A 1997 Phys. Rev. Lett. 79 2983
Google Scholar
[10] Dong L F, Shang J, He Y F, Bai Z G, Liu L, Fan W L 2012 Phys. Rev. E 85 066403
Google Scholar
[11] 梁卓, 罗海云, 王新新, 关志成, 王黎明 2010 59 8739
Google Scholar
Liang Z, Luo H Y, Wang X X, Guan Z C, Wang L M 2010 Acta Phys. Sin. 59 8739
Google Scholar
[12] Mukaigawa S, Fujiwara K, Sato T, Odagiri R, Kudoh T, Yokota A, Oguni K, Takaki K 2016 Jpn. J. Appl. Phys. 55 07LB04
Google Scholar
[13] Hao Y P, Han Y Y, Huang Z M, Yang L, Dai D, Li L C 2018 Phys. Plasmas 25 013516
Google Scholar
[14] Radu I, Bartnikas R, Czeremuszkin G, Wertheimer M R 2003 IEEE Trans. Plasma Sci. 31 411
Google Scholar
[15] Astrov Y A, Ammelt E, Purwins H-G 1997 Phys. Rev. Lett. 78 3129
Google Scholar
[16] 董丽芳, 高瑞玲, 贺亚峰, 范伟丽, 李雪辰, 刘书华, 刘微粒 2007 56 1471
Google Scholar
Dong L F, Gao R L, He Y F, Fan W L, Li X C, Liu S H, Liu W L 2007 Acta Phys. Sin. 56 1471
Google Scholar
[17] Hao Y P, Zheng B, Liu Y G 2014 Phys. Plasmas 21 013503
Google Scholar
[18] Müller I, Ammelt E, Purwins H-G 1999 Phys. Rev. Lett. 82 3428
Google Scholar
[19] Hao Y P, Fang Q, Wan H R, Han Y Y, Yang L, Li L C 2019 Phys. Plasmas 26 073518
Google Scholar
[20] Shirafuji T, Kitagawa T, Wakai T, Tachibana K 2003 Appl. Phys. Lett. 83 2309
Google Scholar
[21] Bedanov V M, Peeters F M 1994 Phys. Rev. B 49 2667
Google Scholar
[22] Boeuf J P, Bernecker B, Callegari T, Blanco S, Fournier R 2012 Appl. Phys. Lett. 100 244108
Google Scholar
[23] 郝艳捧, 刘耀阁, 郑彬 2012 高电压技术 38 1025
Google Scholar
Hao Y P, Liu Y G, Zheng B 2012 High Volt. Eng. 38 1025
Google Scholar
[24] 郝艳捧, 阳林, 涂恩来, 陈建阳 2009 高电压技术 35 1879
Google Scholar
Hao Y P, Yang L, Tu E L, Chen J Y 2009 High Volt. Eng. 35 1879
Google Scholar
[25] Falkenstein Z, Coogan J J 1997 J. Phys. D: Appl. Phys. 30 817
Google Scholar
下载:
计量
- 文章访问数: 6257
- PDF下载量: 72
- 被引次数: 0
