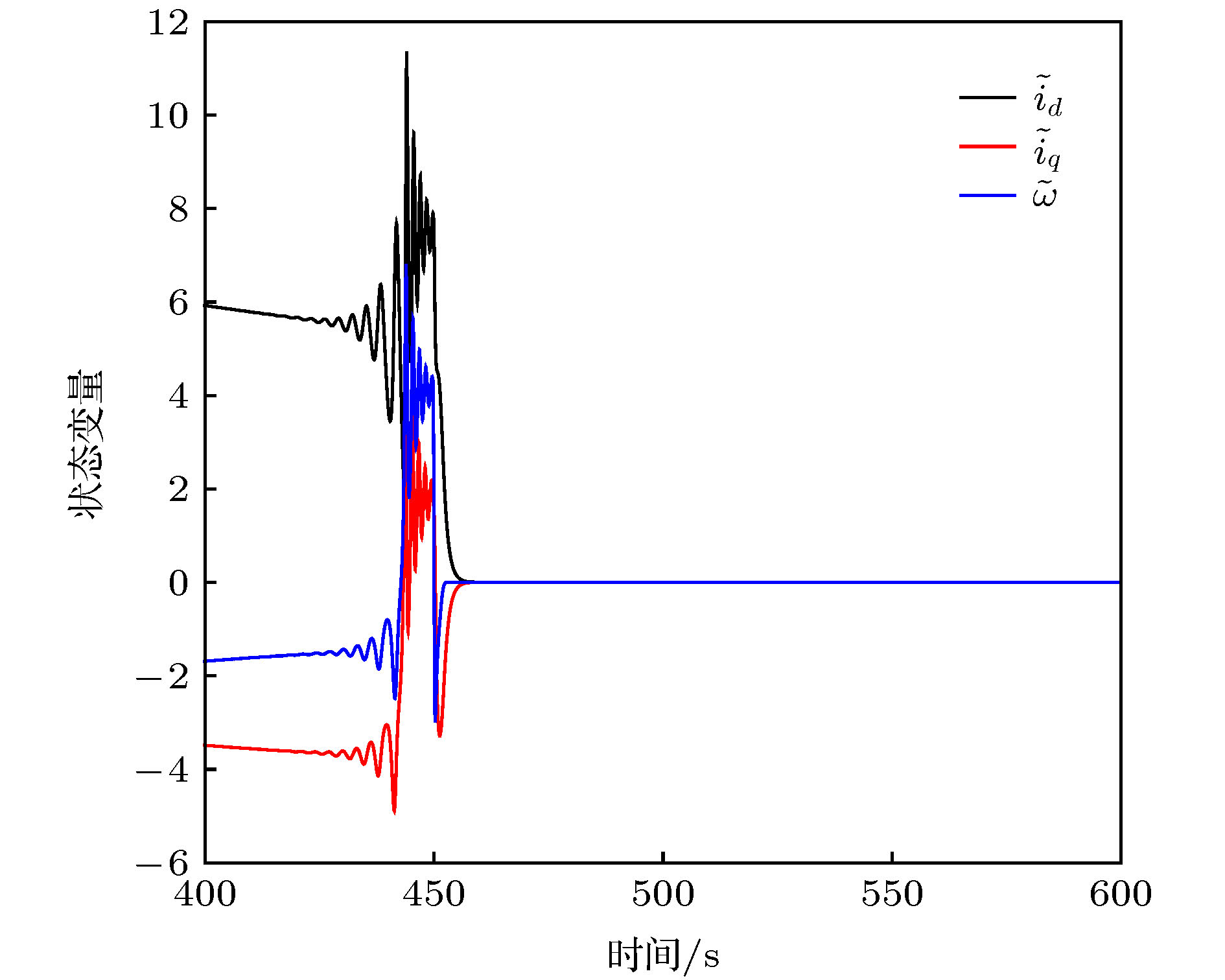
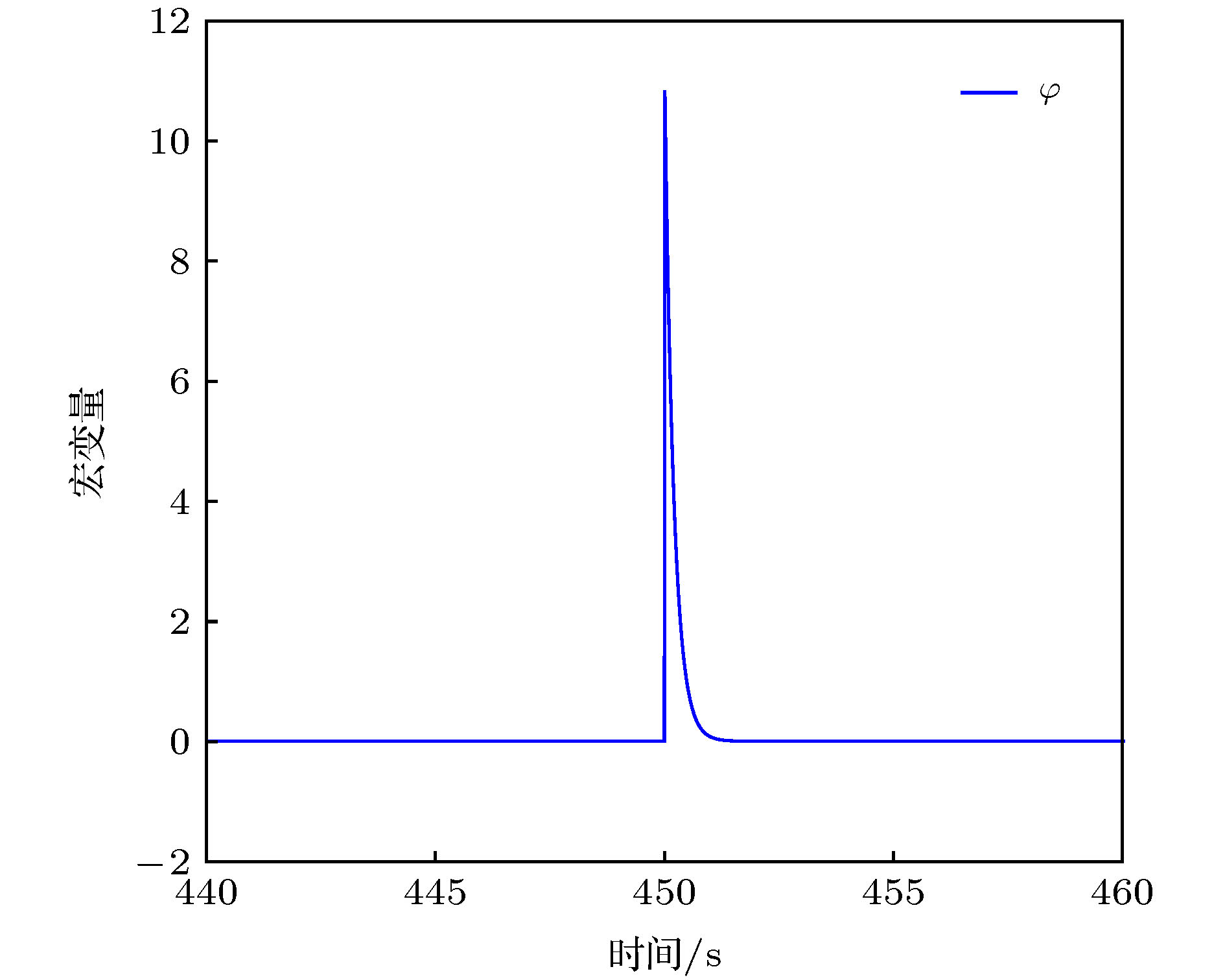
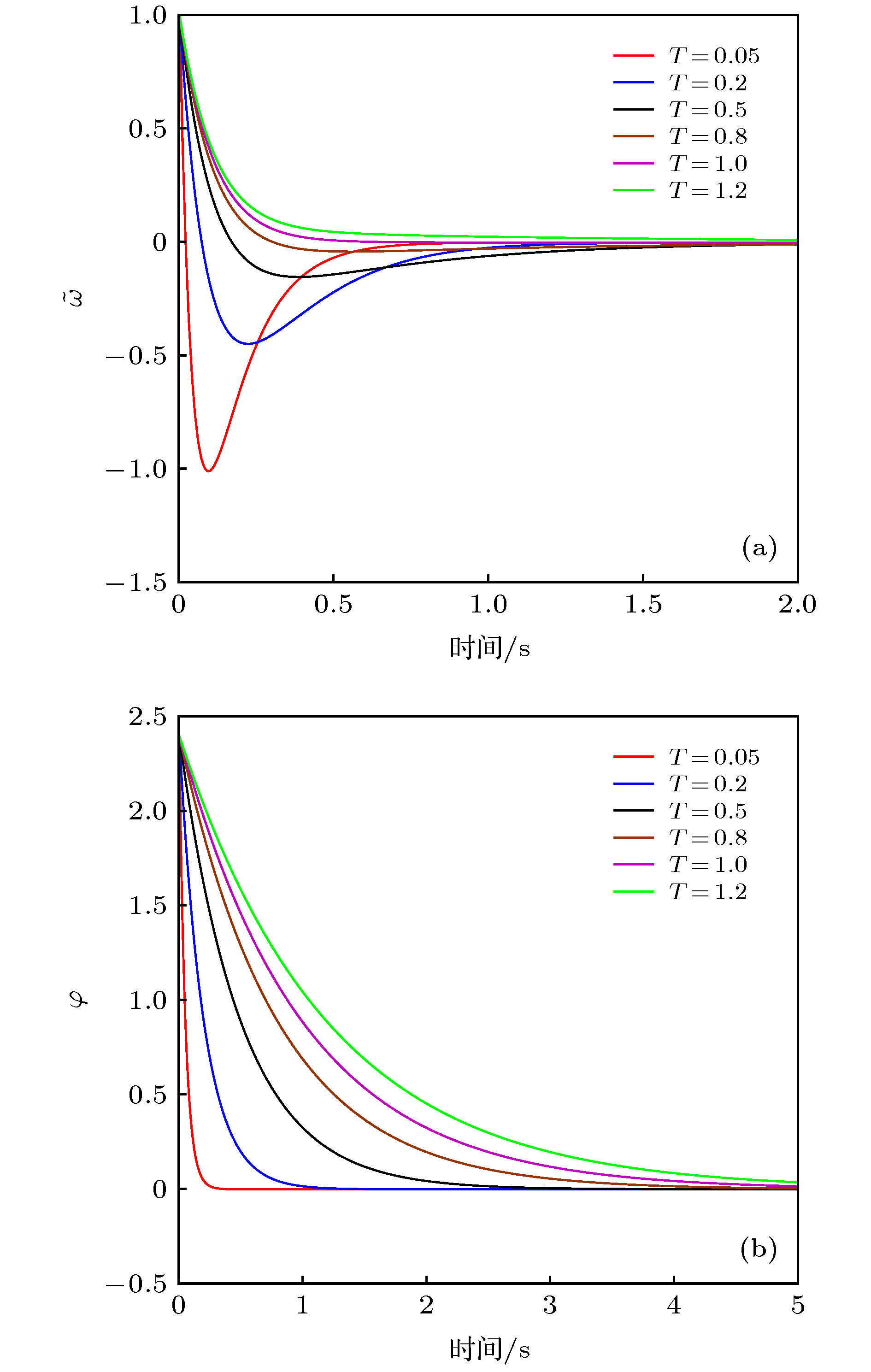
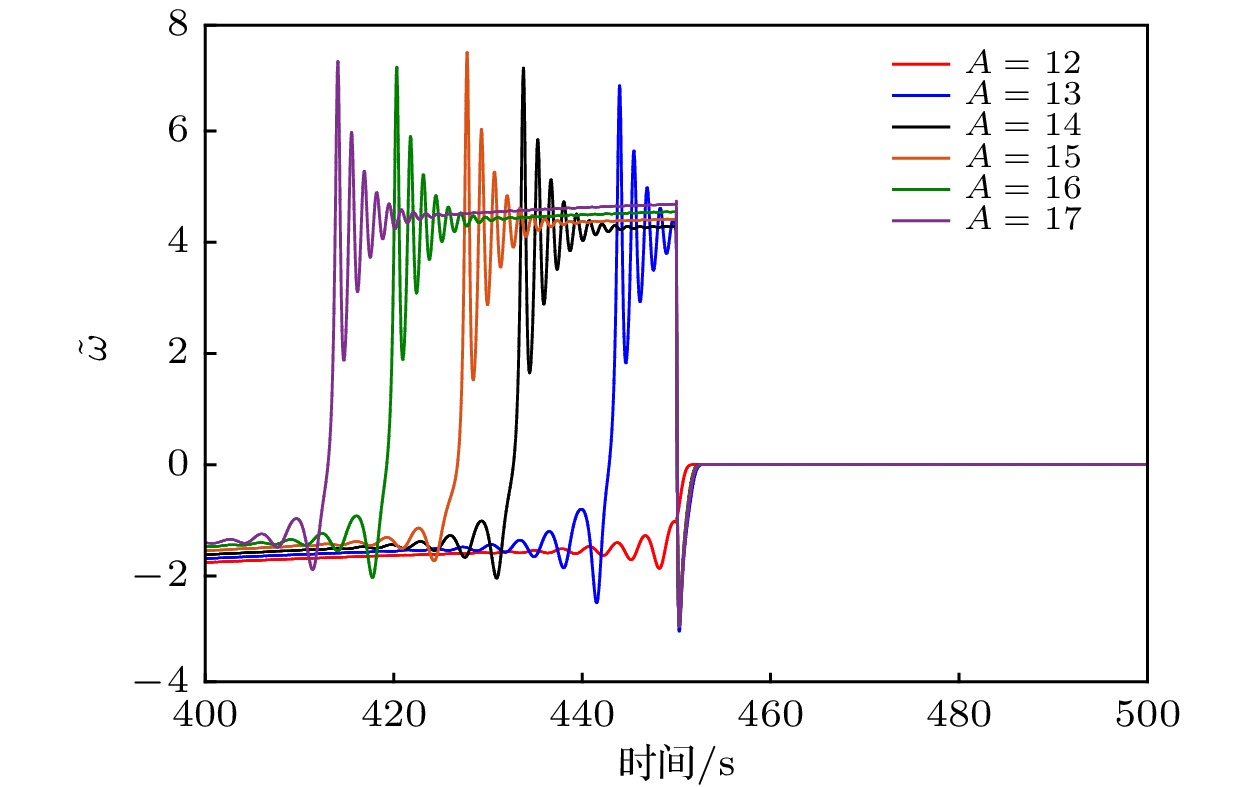
-
以永磁同步电动机系统作为研究对象, 当永磁同步电动机受到周期性外部负载扰动, 且扰动频率与电机系统的固有频率之间存在量级差时, 永磁同步电动机系统中存在快慢耦合效应, 会产生复杂的簇发行为, 严重影响电机的安全稳定运行. 首先利用快慢动力学分析方法将负载扰动项作为系统的慢变参数, 分析系统随慢变参数变化的动力学行为, 揭示了系统“周期性对称式亚临界霍普夫(Hopf)簇发振荡”的演化机理. 其次针对电机系统出现的簇发振荡, 提出了基于协同控制的簇发振荡抑制策略. 通过定义含有所有系统状态的宏变量来设计协同控制器, 当宏变量在控制器作用下收敛到不变流形时, 永磁同步电动机系统也稳定到平衡态. 最后通过理论证明和实验验证该方法的有效性, 仿真结果表明, 协同控制策略在系统存在外部负载扰动时, 具有连续的控制律, 能够有效地快速抑制永磁同步电动机出现的簇发振荡现象, 从而使系统稳定运行.The main purpose of this paper is to reveal the evolution mechanism of the bursting oscillation and suppress the bursting oscillation. The permanent magnet synchronous motor (PMSM) system is taken as a research object, and the case of the PMSM with periodic external load perturbation is considered. The first part in this paper is for the analysis of bursting oscillation. First, a mathematical model of the non-autonomous PMSM system with external load perturbation is established, and the frequency of the external load perturbation is set to be far less than the natural frequency of the PMSM system, so that the PMSM system has a fast-slow coupling effect. Then, the non-autonomous PMSM system with external load perturbation is transformed into a generalized autonomous PMSM system by taking the external load perturbation as a slow-varying parameter of the PMSM system. In order to obtain the bifurcation behaviors and different equilibrium types of the PMSM system, the time series diagram, the equilibrium point distribution curve that changes with slow-varying parameter, and the transformed phase portrait are analyzed. Finally, the evolution mechanism of bursting oscillation is revealed by analyzing the overlay of the equilibrium point distribution curve and the transformed phase portrait, and it is found that the change of the equilibrium type and the corresponding bifurcation behavior will cause the PMSM system to exhibit “periodic symmetrical subcritical Hopf bursting oscillation”. The second part focuses on the control of the bursting oscillation. First, a macro-variable is defined by using the synergetic control strategy, which is a linear combination of all state variables of the PMSM system. Then, the synergetic controller is designed based on the constraint that the macro-variable converges to the invariant manifold. When the macro-variable converges to the invariant manifold, the PMSM system is also stabilized to the equilibrium. In addition, in order to explore the influence of controller parameters, a large number of simulation experiments are carried out, and the relationship between the control parameters with the response speed of the PMSM system is obtained. Finally, the effectiveness of the synergetic control strategy is verified by changing the amplitude of the external load perturbation. The simulation results show that the synergetic control strategy has a continuous control law when the system has external load perturbations, and can effectively suppress the bursting oscillation phenomenon of the PMSM system, so that the PMSM system runs stably.
-
Keywords:
- permanent magnet synchronous motor /
- bursting oscillation /
- synergetic control /
- bursting suppression
[1] Ananthamoorthy N P, Baskaran K 2015 J. Vib. Control 21 181
Google Scholar
[2] Wang L B, Fan J, Wang Z C, Zhan B S, Li J 2016 J. Dyn. Syst. Meas. Contr. 138 011003
Google Scholar
[3] Lu S K, Wang X C, Li Y N 2019 AIP Adv. 9 055105
Google Scholar
[4] Zhang F C, Liao X F, Mu C L 2017 Adv. Differ. Equations 2017 76
Google Scholar
[5] Li Z, Park J B, Joo Y H, Zhang B, Chen G R 2002 IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 49 383
Google Scholar
[6] Singh J P, Roy B K, Kuznetsov N V 2019 Int. J. Bifurcation Chaos 29 1950056
Google Scholar
[7] 罗晓曙, 张波, 丘东元, 韦笃取 2009 58 6026
Google Scholar
Luo X S, Zhang B, Qiu D Y, Wei D Q 2009 Acta Phys. Sin. 58 6026
Google Scholar
[8] 唐传胜, 戴跃洪 2013 62 180504
Google Scholar
Tang C S, Dai Y H 2013 Acta Phys. Sin. 62 180504
Google Scholar
[9] 邢雅清, 陈小可, 张正娣, 毕勤胜 2016 65 090501
Google Scholar
Xing Y Q, Chen X K, Zhang Z D, Bi Q S 2016 Acta Phys. Sin. 65 090501
Google Scholar
[10] 张正娣, 刘杨, 张苏珍, 毕勤胜 2017 66 020501
Google Scholar
Zhang Z D, Liu Y, Zhang S Z, Bi Q S 2017 Acta Phys. Sin. 66 020501
Google Scholar
[11] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[12] Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171
Google Scholar
[13] 吴天一, 陈小可, 张正娣, 张晓芳, 毕勤胜 2017 66 110501
Google Scholar
Wu T Y, Chen X K, Zhang Z D, Zhang X F, Bi Q S 2017 Acta Phys. Sin. 66 110501
Google Scholar
[14] Wu H G, Bao B C, Liu Z, Xu Q, Jing P 2016 Nonlinear Dyn. 83 893
Google Scholar
[15] Wen Z H, Li Z J, Li X 2019 Chaos, Solitons Fractals 128 58
Google Scholar
[16] 李向红, 毕勤胜 2012 61 020504
Google Scholar
Li X H, Bi Q S 2012 Acta Phys. Sin. 61 020504
Google Scholar
[17] Razvan M R, Yasaman S 2020 Chaos, Solitons Fractals 132 109482
Google Scholar
[18] Ryashko L, Slepukhina E 2020 Commun. Nonlinear Sci. Numer. Simul. 82 105071
Google Scholar
[19] Han X J, Zhang Y, Bi Q S, Kurths J 2018 Chaos: An Interdiscip. J. Nonlinear Sci. 28 043111
Google Scholar
[20] Peng M, Zhang Z D, Qu Z F, Bi Q S 2020 Pramana - J. Phys. 94 14
Google Scholar
[21] Yu Y, Zhang Z D, Han X J 2018 Commun. Nonlinear Sci. Numer. Simul. 56 380
Google Scholar
[22] Zhang Z D, Chen Z Y, Bi Q S 2019 Theor. Appl. Mech. Lett. 9 358
Google Scholar
[23] Han X J, Xia F B, Zhang C, Yu Y 2017 Nonlinear Dyn. 88 2693
Google Scholar
[24] Bi Q S, Ma R, Zhang Z D 2015 Nonlinear Dyn. 79 101
Google Scholar
[25] Wei D Q, Zhang B, Luo X S 2012 Chin. Phys. B 21 030504
Google Scholar
[26] Han X J, Bi Q S 2011 Commun. Nonlinear Sci. Numer. Simul. 16 4146
Google Scholar
[27] 王江彬, 刘崇新 2020 西安交通大学学报 54 26
Google Scholar
Wang J B, Liu C X 2020 J. Xi'an Jiaotong Univ. 54 26
Google Scholar
[28] Wang J B, Liu L, Liu C X 2019 Int. J. Bifurcation Chaos 29 1950130
Google Scholar
-
图 2
$\tilde \omega $ 关于慢变参数${\tilde T_{\rm{L}}}$ 的平衡点分布曲线Fig. 2. Equilibrium point distribution curve of
$\tilde \omega $ with respect to the slow-varying parameter${\tilde T_{\rm{L}}}$ .
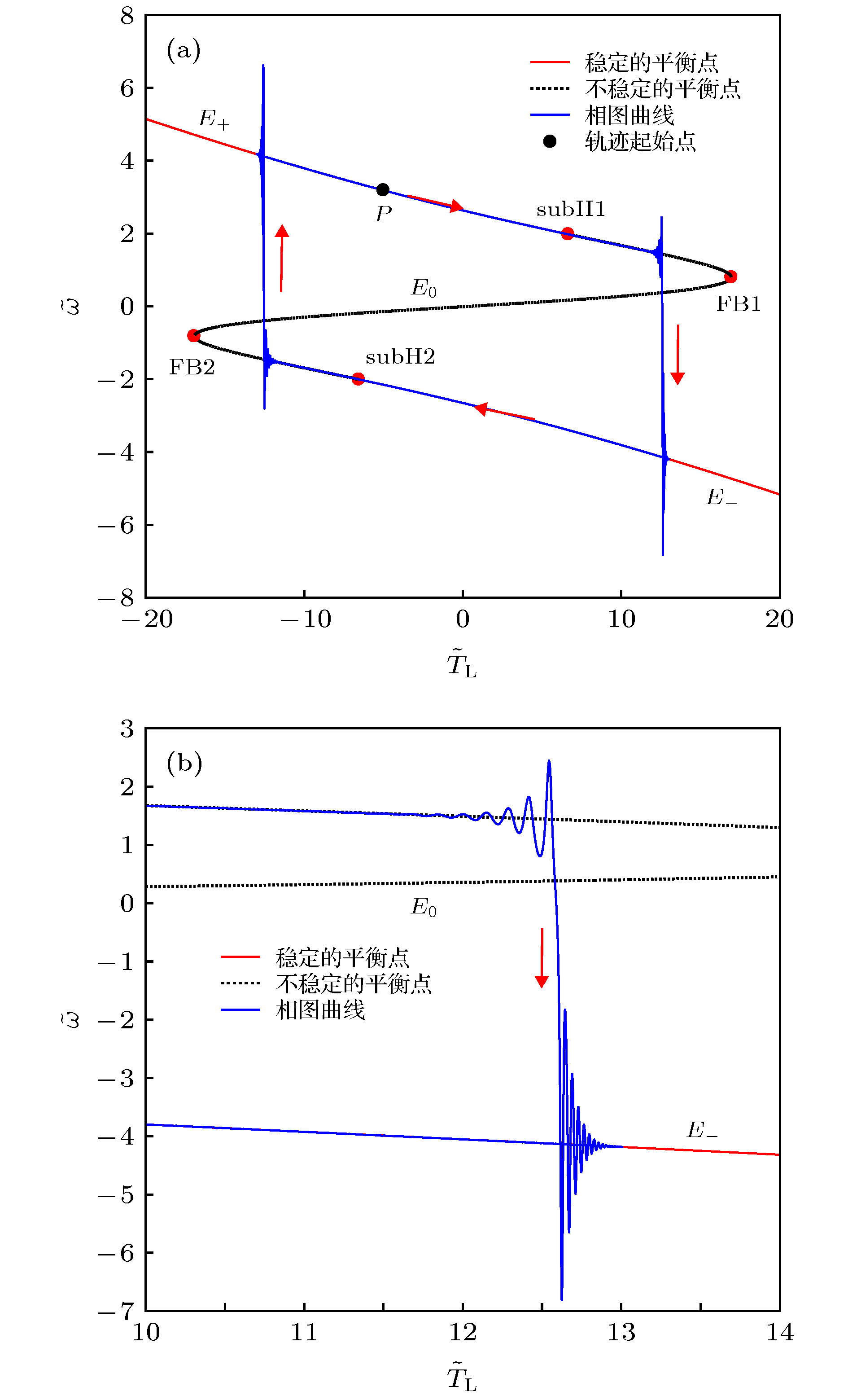
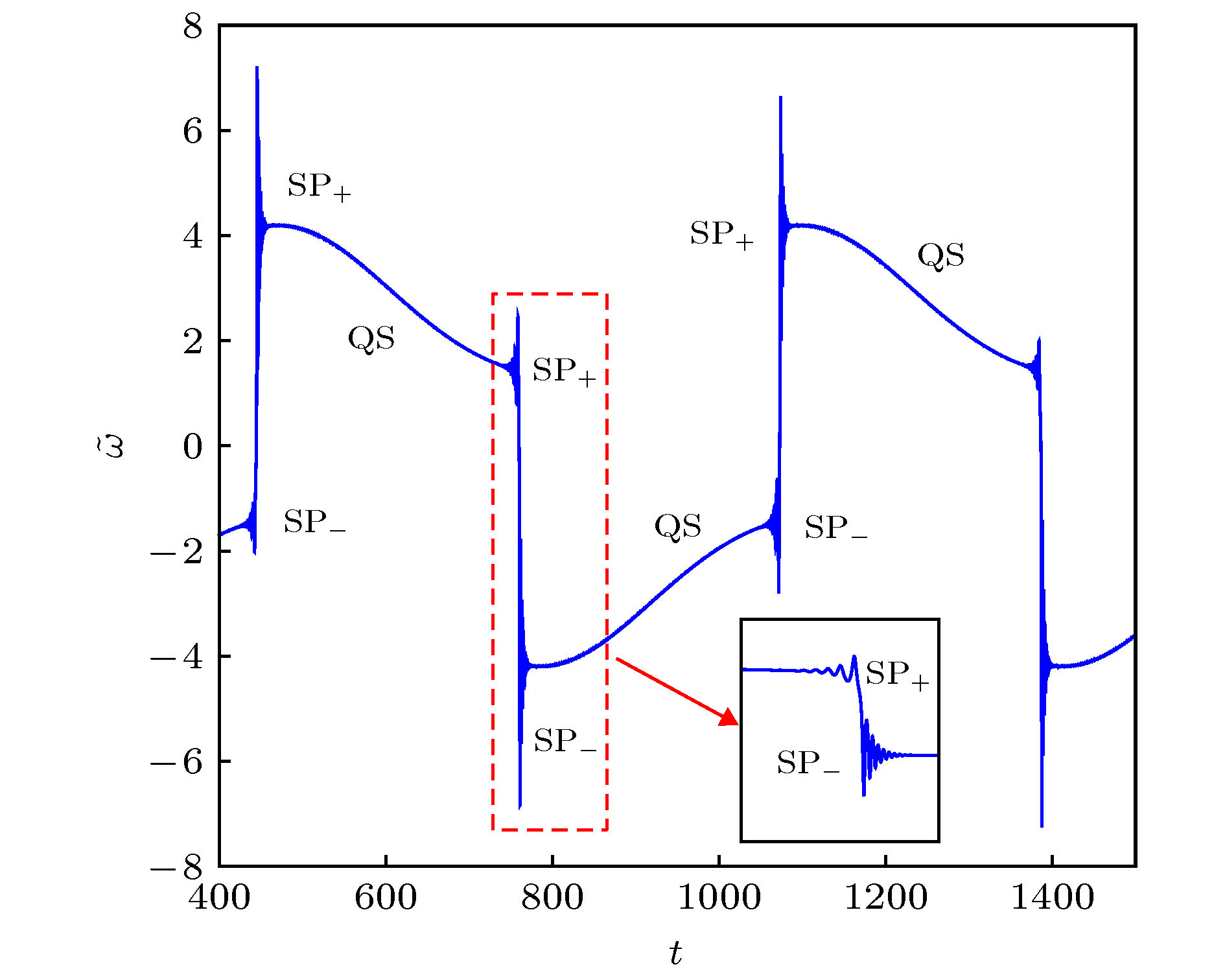
图 3 转子机械角速度
$\tilde \omega $ 的簇发振荡示意图 (a) (${\tilde T_{\rm{L}}}$ ,$\tilde \omega $ )平面上的转换相图与平衡点分布曲线的叠加图; (b) 图3(a)的局部放大图Fig. 3. Bursting Oscillation of
$\tilde \omega $ : (a) Overlay of the transformed phase portrait and equilibrium point distribution curve on the (${\tilde T_L}$ ,$\tilde \omega $ ) plane; (b) locally enlarged diagram of Fig. 3(a).
图 7 PMSM系统和宏变量
$\varphi $ 随参数T变化的响应曲线 (a)$\tilde \omega $ 的响应曲线; (b) 宏变量$\varphi $ 的响应曲线Fig. 7. Response curves of PMSM system and macro-variable
$\varphi $ as T changes: (a) Response curves of$\tilde \omega $ ; (b) response curves of macro-variable$\varphi $ .
图 8 PMSM系统和宏变量
$\varphi $ 随参数${k_3}$ 变化的响应曲线 (a)$\tilde \omega $ 的响应曲线; (b) 宏变量$\varphi $ 的响应曲线Fig. 8. Response curves of PMSM system and macro-variable
$\varphi $ as${k_3}$ changes: (a) Response curves of$\tilde \omega $ ; (b) response curves of macro-variable$\varphi $ .
图 9 不同扰动下的PMSM系统的状态响应
Fig. 9. State response of PMSM system under different perturbations.
-
[1] Ananthamoorthy N P, Baskaran K 2015 J. Vib. Control 21 181
Google Scholar
[2] Wang L B, Fan J, Wang Z C, Zhan B S, Li J 2016 J. Dyn. Syst. Meas. Contr. 138 011003
Google Scholar
[3] Lu S K, Wang X C, Li Y N 2019 AIP Adv. 9 055105
Google Scholar
[4] Zhang F C, Liao X F, Mu C L 2017 Adv. Differ. Equations 2017 76
Google Scholar
[5] Li Z, Park J B, Joo Y H, Zhang B, Chen G R 2002 IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 49 383
Google Scholar
[6] Singh J P, Roy B K, Kuznetsov N V 2019 Int. J. Bifurcation Chaos 29 1950056
Google Scholar
[7] 罗晓曙, 张波, 丘东元, 韦笃取 2009 58 6026
Google Scholar
Luo X S, Zhang B, Qiu D Y, Wei D Q 2009 Acta Phys. Sin. 58 6026
Google Scholar
[8] 唐传胜, 戴跃洪 2013 62 180504
Google Scholar
Tang C S, Dai Y H 2013 Acta Phys. Sin. 62 180504
Google Scholar
[9] 邢雅清, 陈小可, 张正娣, 毕勤胜 2016 65 090501
Google Scholar
Xing Y Q, Chen X K, Zhang Z D, Bi Q S 2016 Acta Phys. Sin. 65 090501
Google Scholar
[10] 张正娣, 刘杨, 张苏珍, 毕勤胜 2017 66 020501
Google Scholar
Zhang Z D, Liu Y, Zhang S Z, Bi Q S 2017 Acta Phys. Sin. 66 020501
Google Scholar
[11] Hodgkin A L, Huxley A F 1952 J. Physiol. 117 500
Google Scholar
[12] Izhikevich E M 2000 Int. J. Bifurcation Chaos 10 1171
Google Scholar
[13] 吴天一, 陈小可, 张正娣, 张晓芳, 毕勤胜 2017 66 110501
Google Scholar
Wu T Y, Chen X K, Zhang Z D, Zhang X F, Bi Q S 2017 Acta Phys. Sin. 66 110501
Google Scholar
[14] Wu H G, Bao B C, Liu Z, Xu Q, Jing P 2016 Nonlinear Dyn. 83 893
Google Scholar
[15] Wen Z H, Li Z J, Li X 2019 Chaos, Solitons Fractals 128 58
Google Scholar
[16] 李向红, 毕勤胜 2012 61 020504
Google Scholar
Li X H, Bi Q S 2012 Acta Phys. Sin. 61 020504
Google Scholar
[17] Razvan M R, Yasaman S 2020 Chaos, Solitons Fractals 132 109482
Google Scholar
[18] Ryashko L, Slepukhina E 2020 Commun. Nonlinear Sci. Numer. Simul. 82 105071
Google Scholar
[19] Han X J, Zhang Y, Bi Q S, Kurths J 2018 Chaos: An Interdiscip. J. Nonlinear Sci. 28 043111
Google Scholar
[20] Peng M, Zhang Z D, Qu Z F, Bi Q S 2020 Pramana - J. Phys. 94 14
Google Scholar
[21] Yu Y, Zhang Z D, Han X J 2018 Commun. Nonlinear Sci. Numer. Simul. 56 380
Google Scholar
[22] Zhang Z D, Chen Z Y, Bi Q S 2019 Theor. Appl. Mech. Lett. 9 358
Google Scholar
[23] Han X J, Xia F B, Zhang C, Yu Y 2017 Nonlinear Dyn. 88 2693
Google Scholar
[24] Bi Q S, Ma R, Zhang Z D 2015 Nonlinear Dyn. 79 101
Google Scholar
[25] Wei D Q, Zhang B, Luo X S 2012 Chin. Phys. B 21 030504
Google Scholar
[26] Han X J, Bi Q S 2011 Commun. Nonlinear Sci. Numer. Simul. 16 4146
Google Scholar
[27] 王江彬, 刘崇新 2020 西安交通大学学报 54 26
Google Scholar
Wang J B, Liu C X 2020 J. Xi'an Jiaotong Univ. 54 26
Google Scholar
[28] Wang J B, Liu L, Liu C X 2019 Int. J. Bifurcation Chaos 29 1950130
Google Scholar
下载:
计量
- 文章访问数: 6538
- PDF下载量: 117
- 被引次数: 0
