-
氢致裂纹是制约超高强度钢应用的关键问题, 掌握扩散氢的分布行为有助于弄清氢致裂纹的形成机理. 本文采用第一性原理方法计算了H原子占据α-Fe晶格间隙和空位时的情况, 得到了晶体的稳定构型及能量, 并据此分析了H原子在晶格间隙和空位中的溶解倾向; 从Mulliken布居、电子密度分布、态密度分布等角度分析了H原子与α-Fe晶体间隙和空位之间的相互作用. 结果表明: 间隙H原子倾向占据α-Fe四面体间隙位, 其1s轨道电子与Fe的4s轨道电子呈微弱共轭杂化; 空位是强氢陷阱, H原子倾向占据空位内壁附近的等电荷面. 在真空0 K条件下单空位最多稳定溶解3个H原子, 且H原子之间未表现出自发形成H2的倾向; 间隙和空位中的H原子溶入改变了Fe晶格内电子分布导致原子结合力弱化, 并在局部区域形成反键. 基于第一性原理能量计算结果开展热力学分析, 分析结果表明大多数情况下间隙H原子都是H主要的固溶形式, H平衡溶解度计算结果与实际符合良好.Hydrogen-induced cracking (HIC) is a key problem restricting the application of ultra-high strength steel. It is necessary to analyze the distribution of diffusible hydrogen to reveal the mechanism of HIC. The site occupation tendency of H in interstitial and vacancy positions are investigated by the ab-initio method, and the stable configuration and steady state energy are obtained. The solution tendency of H atom in interstitial and vacancy positions is analyzed based on the aforementioned results. Specifically, the Mulliken population, density of states, charge density difference are calculated and used to analyze the interaction between α-Fe metal and H atom. The results show that the dissolved H tends to occupy the interstitial sites of the body-centered cubic, the weak hybridization interaction between the interstitial hydrogen and its nearest neighbour Fe atom is contributed by the H 1s orbital and Fe 4s orbital. Vacancies can capture H atoms easily and H atoms tend to occupy the isoelectric surface near the inwall of the vacancies. A vacancy defect can hold up to three H atoms which are difficult to combine with each other to form H2 molecule by covalent bond. H atoms in vacancies and at interstitial positions change the charge distribution of the Fe lattice, which weakens the binding force of the atoms and forms anti-bonding orbital in local area. The proposed thermodynamical model allows the determining of the equilibrium vacancy and the dissolved H concentration for a given temperature and H chemical potential in the reservoir, and the calculated results are in good agreement with the actual results.
-
Keywords:
- density functional theory /
- thermodynamic analysis /
- ferrite /
- diffusible hydrogen
[1] 张文钺 1999 焊接冶金学(基本原理)(北京: 机械工业出版社) 第241—244页
Zhang W Y 2012 Welding Metallurgy (Fundamental Principle) (Beijing: China Machine Press) pp241–244 (in Chinese)
[2] 张敬强 2015 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhang J Q 2015 Ph.D Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[3] Tateyama Y, Ohno T 2003 ISIJ Internation 43 573
Google Scholar
[4] Geng W T, Wan L, Du J P, Ogata S 2017 Scripta Materialia 134 105
Google Scholar
[5] MonasterioP R, Lau T T, Yip S, van Vliet K J 2009 Phys. Rev. Lett. 103 085501
Google Scholar
[6] Nagumo M, Nakamura M, Taika K 2001 Metall. Mater. Trans. A 32 339
Google Scholar
[7] Först C J, Slycke J, van Vliet K J, Yip S 2006 Phys. Rev. Lett. 96 175501
Google Scholar
[8] Fukai Y 1983 Jpn. J. Appl. Phys. 22 207
Google Scholar
[9] 张凤春, 李春福, 文平, 罗强, 冉曾令 2014 63 227101
Google Scholar
ZhangF C, Li C F, Wen P, Luo Q, Ran Z L 2014 Acta Phys. Sin. 63 227101
Google Scholar
[10] Du Y A, Ismer L, Rogal J, Hickel T, Neugebauer J, Drautz R 2011 Phys. Rev. B 84 144121
Google Scholar
[11] Nazarov R, Hickel T, Neugebauer J 2014 Phys. Rev. B 89 144108
Google Scholar
[12] Nazarov R, Hickel T, Neugebauer J 2012 Phys. Rev. B 85 144118
Google Scholar
[13] Hickel T, Grabowski B, Körmann F, Neugebauer J 2011 J. Phys. Condens. Mater. 24 053202
Google Scholar
[14] Ramasubramaniam A, Itakura M, Carter EA 2009 Phys. Rev. B 79 174101
Google Scholar
[15] Payne M C, Teter M P, Allan D C, Arias T A, Joannopoulos J D 1992 Rev. Mod. Phys. 64 1045
Google Scholar
[16] Milman V, Winkler B, White JA, Pickard C J, Payne M C, Akhmataskaya E V, Nobes R H 2000 Int. J. Quantum Chem. 77 895
Google Scholar
[17] Perdew JP, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[18] Methfessel M, Paxton A T 1989 Phys. Rev. B 40 3616
Google Scholar
[19] Acet M, Zähres H, Wassermann E F, Pepperhoff W 1994 Phys. Rev. B 49 6012
Google Scholar
[20] Hayward E, Fu C C 2013 Phys. Rev. B 87 174103
Google Scholar
[21] Baroni S, de Gironcoli S, Dal Corso A C, Giannozzi P 2001 Rev. Mod. Phys. 73 515
Google Scholar
[22] Bozzolo G, Ferrante J 1992 Phys. Rev. B 46 8600
Google Scholar
[23] Bhatia M A, Groh S, Solanki K N 2014 J. Appl. Phys. 116 064302
Google Scholar
[24] Tateyama Y, Ohno T 2003 Phys. Rev. B 67 174105
Google Scholar
[25] Mclellan R B, Harkins C G 1975 Mater. Sci. Eng. 18 5
Google Scholar
[26] Lynch SP 2013 Metall. Mater. Trans. A 44 1209
Google Scholar
[27] Lu G, Kaxiras E 2005 Phys. Rev. Lett. 94 155501
Google Scholar
[28] Ismer L, Hickel T, Neugebauer J 2010 Phys. Rev. B 81 094111
Google Scholar
[29] Korzhavyi P A, Abrikosov I A, Johansson B, Ruban A V, Skriver H L 1999 Phys. Rev. B 59 11693
Google Scholar
[30] Nazarov R, Hickel T, Neugebauer J 2010 Phys. Rev. B 82 224104
Google Scholar
[31] Speight J G 2005 Lange’s Handbook of Chemistry (16th Ed.) (New York: The McGraw-Hill Companies, Inc) pp1299−1309
-
图 1 α-Fe+H的晶体结构 (a) T-site; (b) O-site
Fig. 1. Crystalline structure of α-Fe+H: (a) T-site; (b) O-site.
图 2 α-Fe+H (T-site)的分波电子态密度 (a) 固溶前后 H 原子; (b) 固溶前后最近邻Fe原子; (c) 四面体间隙H原子; (d) 间隙H原子最近邻Fe原子
Fig. 2. Partial electronic density of state of α-Fe+H (T-site): (a) Free H atom and interstitial H atom; (b) Fe atom in perfect α-Fe crystal and the nearest neighbour of interstitial H atom; (c) H atom in tetrahedral interstice; (d) the nearest neighbour Fe atom of interstitial H atom.
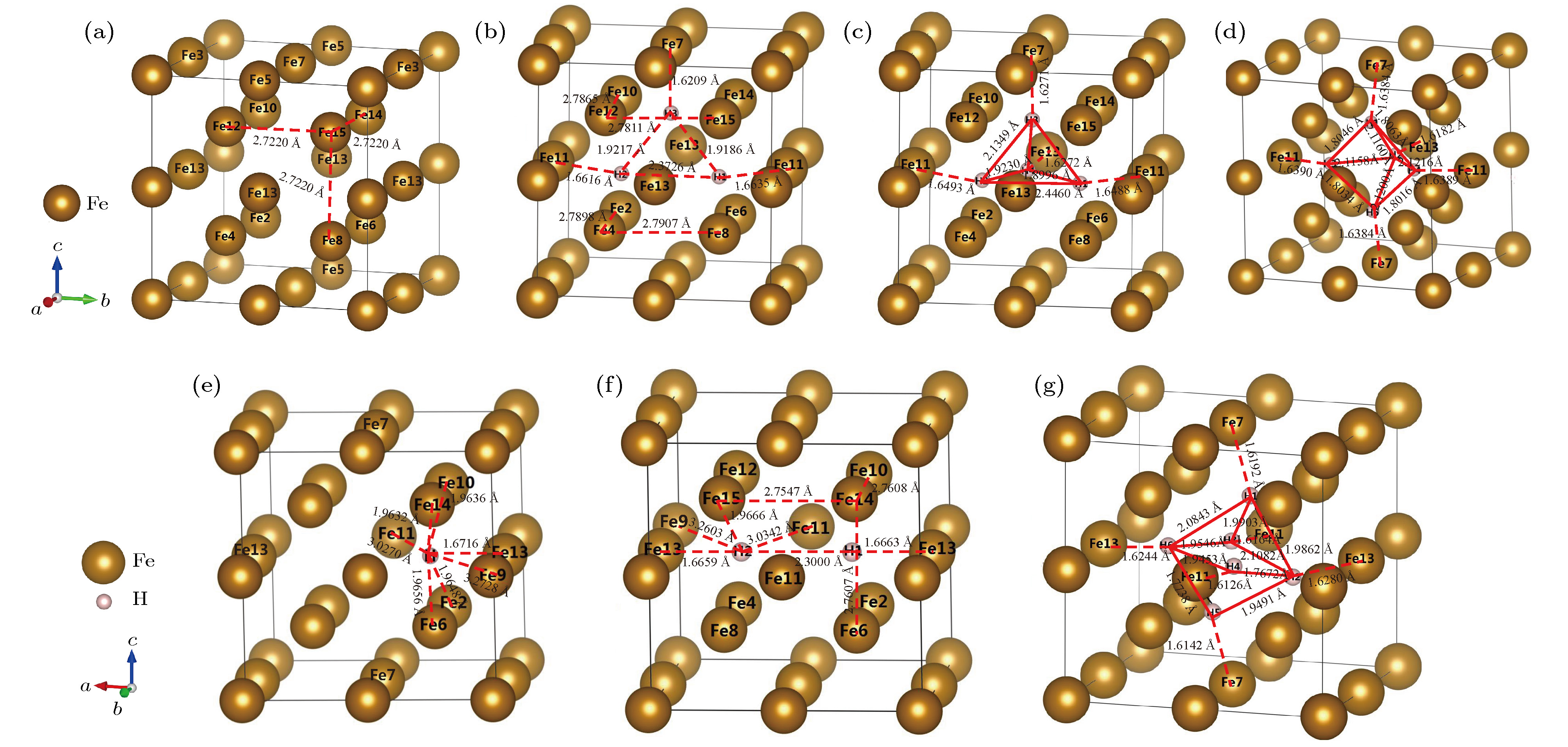
图 4 α-Fe+(nH-Vac)的晶体结构 (a) α-Fe+Vac; (b) α-Fe+(3H-Vac); (c) α-Fe+(4H-Vac); (d) α-Fe+(5H-Vac); (e) α-Fe+(1H-Vac); (f) α-Fe+(2H-Vac); (g) α-Fe+(6H-Vac)
Fig. 4. Crystalline structure of α-Fe+(nH-Vac): (a) α-Fe+Vac; (b)α-Fe+(3H-Vac); (c) α-Fe+(4H-Vac); (d) α-Fe+(5H-Vac); (e) α-Fe+(1H-Vac); (f) α-Fe+(2H-Vac); (g) α-Fe+(6H-Vac).
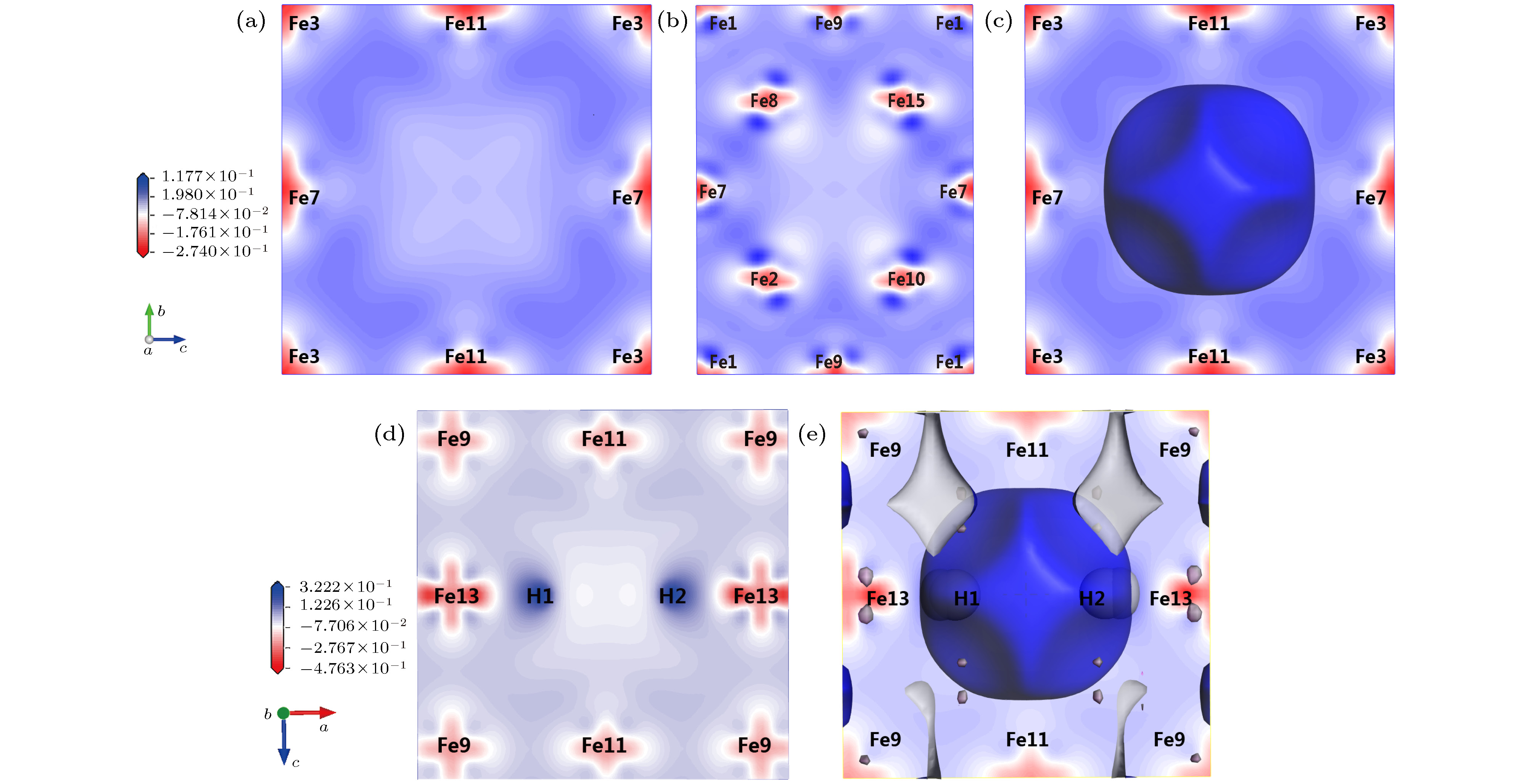
图 5 α-Fe+(nH-Vac)的等电荷面和差分电荷密度 (a) α-Fe+Vac ((100)面); (b) α-Fe+Vac ((110)面); (c) α-Fe+Vac等电荷面; (d) α-Fe+(2H-Vac) ((010)面); (e) α-Fe+(2H-Vac)等电荷面
Fig. 5. Isoelectronic density surface and electron density difference of α-Fe+(nH-Vac): (a) Electron density difference of α-Fe+Vac in surface (100); (b) electron density difference of α-Fe+Vac in surface (110); (c) isoelectric density surface of α-Fe+Vac; (d) electron density difference of α-Fe+(2H-Vac) in surface (010); (e) isoelectric density surface of α-Fe+(2H-Vac).
图 7 0 K下缺陷形成能随μH变化情况
Fig. 7. Formation energy of defects at 0 K for different H chemical potentials.
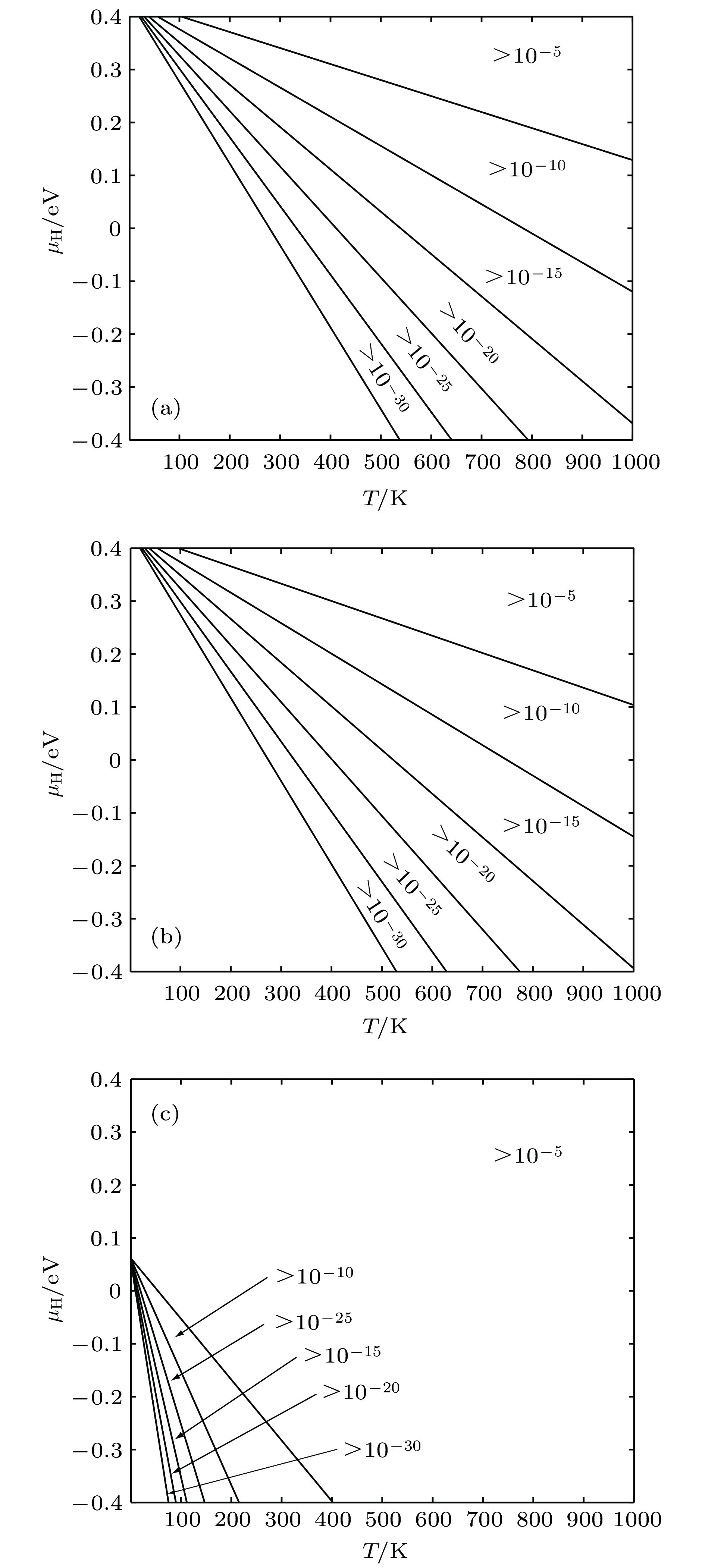
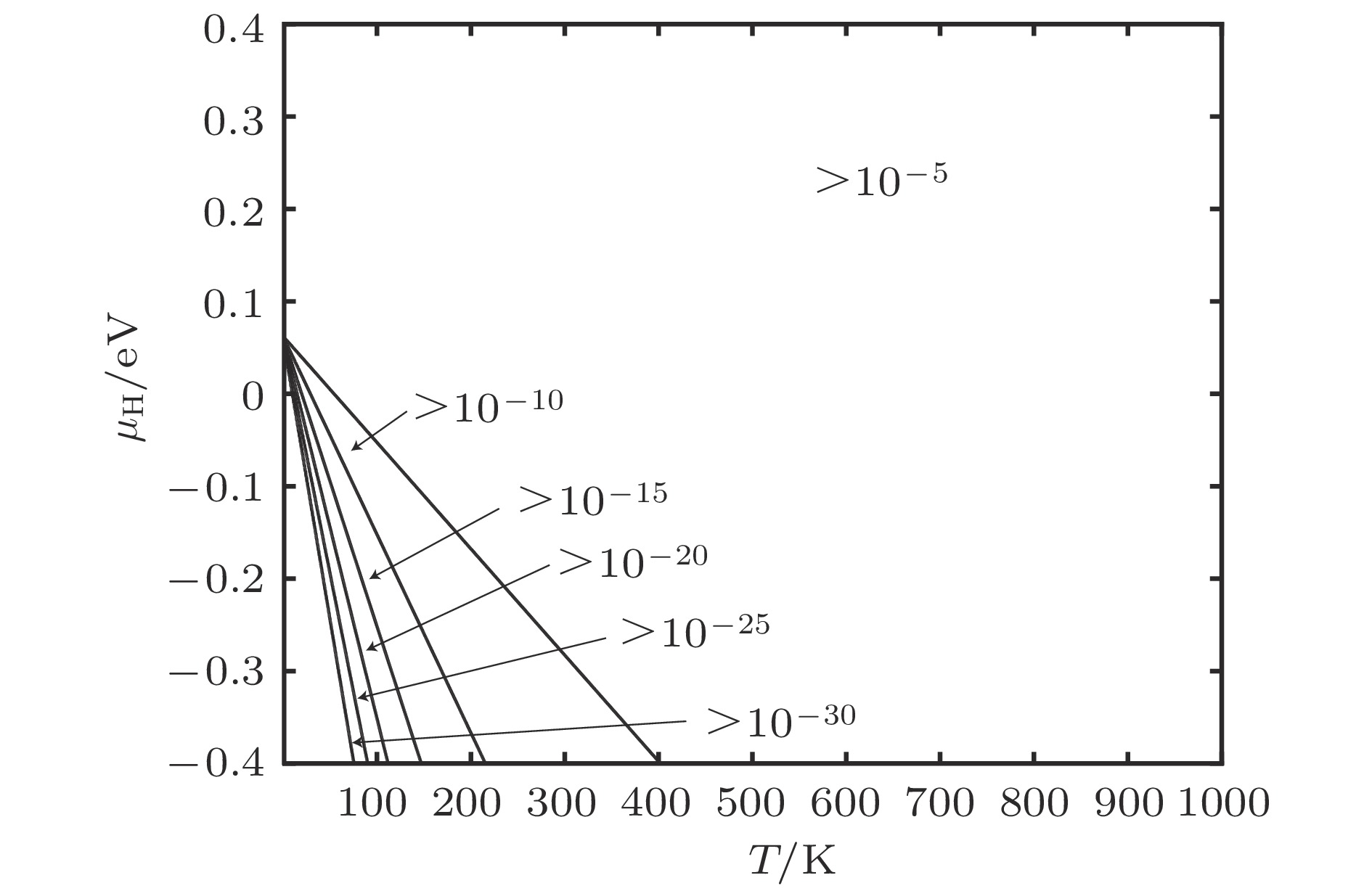
图 8 缺陷随T和μH变化情况 (a) 空位平衡浓度; (b) 空位内H平衡浓度; (c) 间隙H平衡浓度
Fig. 8. Equilibrium concentration of defects for different temperature and H chemical potentials: (a) Equilibrium concentration of vacancies; (b) equilibrium concentration of H occupying in vacancies; (c) equilibrium concentration of H occupying in interstitial positions.
图 9 含空位α-Fe晶体H总平衡浓度
Fig. 9. Equilibrium total concentration of H of α-Fe containing vacancies.
图 10 Devnathan-Stachurski双电解池示意图
Fig. 10. Schematic diagram of Devnathan-Stachurski double electrolytic cell.
表 1 α-Fe+H的晶格常数和晶体结构
Table 1. Lattice parameters and crystalline structure of α-Fe+H.
晶体类型 a/Å b/Å c/Å α/(°) β/(°) γ/(°) V/Å 空间群 α-Fe+H(T-site) 5.6843 5.6612 5.6804 89.999 89.999 90.000 5.6843 115(P-4m2) α-Fe+H(O-site) 5.8019 5.6112 5.6112 90.000 90.000 90.000 5.8019 123(P4/mmm) 
下载: 导出CSV
表 2 α-Fe和α-Fe+H结合能、形成能和溶解热
Table 2. Binding energy, formation energy, and heat of solution of α-Fe and α-Fe+H.
晶体类型 ${E_{{\rm{crystal}}}}$/eV ${E_{{\rm{ZP}}}}$/eV ${E_{{\rm{bind}}}}$/eV $E_{{\rm{form}}}$/eV $\Delta H_{{ {\rm{sol} } } }^{\rm{H} }$/eV α-Fe+H(T-site) –13861.050 0.246 5.182 0.390 0.390 α-Fe –13845.344 — 5.530 —
下载: 导出CSV
表 3 α-Fe+H (T-site)晶体原子轨道布居
Table 3. Atomic orbital population of α-Fe+H (T-site).
晶体类型 原子 轨道电荷占据数 总布居 净布居 s p d α-Fe-H(T-site) H 1.34 0 0 1.34 –0.34 Fe2, Fe4 0.62 0.66 6.65 7.93 0.07 Fe3, Fe11 0.62 0.67 6.65 7.94 0.06 Fe12, Fe10 0.65 0.72 6.62 7.99 0.01 Fe1, Fe9, Fe13, Fe14, Fe16 0.65 0.72 6.62 7.99 0.01 Fe8, Fe6 0.65 0.74 6.61 8.01 –0.01 α-Fe Fe 0.68 0.70 6.62 8.00 0 自由态 H 1.00 0 0 1.00 0
下载: 导出CSV
表 4 α-Fe-H (T-site)晶体键布居
Table 4. Bond population of α-Fe+H (T-site).
晶体类型 原子对 距离/Å 键布居 α-Fe-H (T-site) Fe2-H 1.6494 0.16 Fe3-H 1.6507 0.16 Fe2-Fe3 2.5558 –0.09 Fe2-Fe4 2.7286 –0.14 Fe8-Fe11 2.4783 0.17 Fe3-Fe12 2.4471 0.18 Fe8-Fe16 2.8401 0.05 Fe7-Fe8 2.4601 0.15 α-Fe-H (O-site) Fe2-Fe4 2.6287 –0.28 α-Fe Fe-Fe 2.4400 0.14 Fe-Fe 2.8174 0.06
下载: 导出CSV
表 5 α-Fe+(nH-Vac)的晶格常数和晶体结构
Table 5. Lattice parameters and crystalline structure of α-Fe+(nH-Vac).
晶体类型 a/Å b/Å c/Å α/(°) β/(°) γ/(°) V/Å 空间群 α-Fe+Vac 5.6033 5.6033 5.6033 90.000 90.000 90.000 175.923 221${\rm{(}}Pm\overline {{\rm{3}}m} )$ α-Fe+(Vac-1H) 5.6321 5.6103 5.6103 90.000 90.001 89.999 177.270 99${\rm{(}}P{\rm{4}}MM)$ α-Fe+(Vac-2H) 5.6285 5.6285 5.6484 90.000 90.000 90.000 178.940 123(P4/MMM) α-Fe+(Vac-3H) 5.6297 5.6598 5.6853 90.004 90.011 90.002 181.154 25(PMM2) α-Fe+(Vac-4H) 5.6727 5.6943 5.6723 89.966 90.540 89.973 183.221 38(AMM2) α-Fe+(Vac-5H) 5.6905 5.7086 5.7093 90.000 90.004 90.002 185.467 99${\rm{(}}P{\rm{4}}MM)$ α-Fe+(Vac-6H) 5.7407 5.7270 5.7208 89.433 89.691 89.692 188.064 5(C2)
下载: 导出CSV
表 6 α-Fe+(nH-Vac)的结合能、形成能和溶解热
Table 6. Binding energy, formation energy, and heat of solution of α-Fe+(nH-Vac).
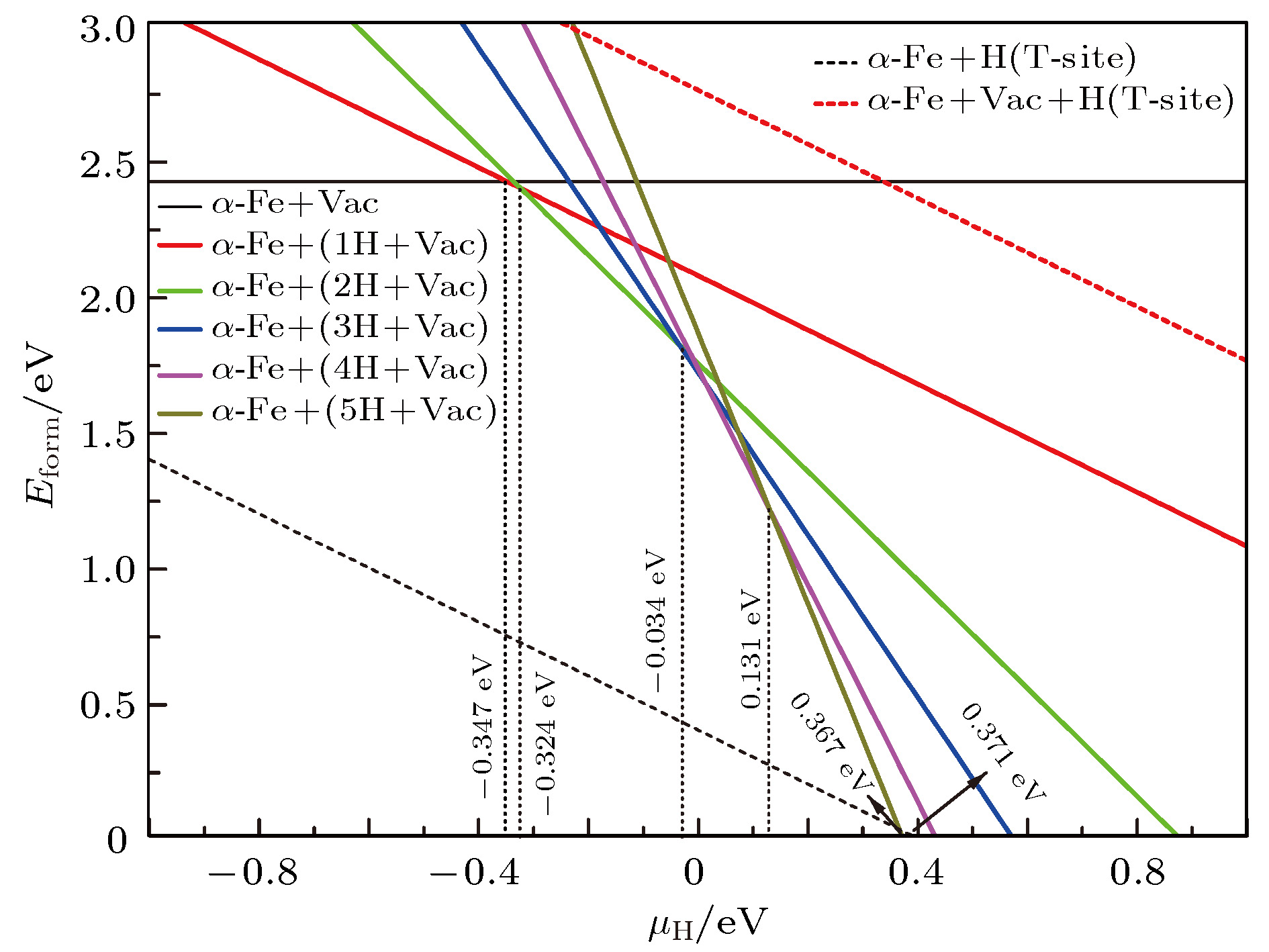
晶体类型 ${E_{{\rm{crystal}}}}$/eV ${E_{{\rm{ZP}}}}$/eV ${E_{{\rm{bind}}}}$/eV $E_{{\rm{form}}}$/eV $\Delta H_{_{ {\rm{sol} } } }^{\rm{H} }$/eV α–Fe+Vac –12977.593 — 5.369 2.416 — α–Fe+(Vac-1H) –12993.933 0.141 5.055 1.928 –0.347 α–Fe+(Vac-2H) –13010.262 0.295 4.777 1.450 –0.324 α–Fe+(Vac-3H) –13026.330 0.478 4.513 1.234 –0.034 α–Fe+(Vac-4H) –13042.359 0.670 4.275 1.056 0.014 α–Fe+(Vac-5H) –13058.299 0.889 4.055 0.968 0.131 α–Fe+(Vac-6H) –13073.995 1.149 3.842 1.123 0.438
下载: 导出CSV
表 7 α-Fe+(nH-Vac)对H原子的陷阱能
Table 7. Hydrogen trapping energy of α-Fe+(nH-Vac)
晶体类型 $E_{{\rm{trap}}}^{\rm{H}}$/eV 不考虑${E_{{\rm{ZP}}}}$ 考虑${E_{{\rm{ZP}}}}$ α-Fe+(Vac-1H) 0.633 0.778 α-Fe+(Vac-2H) 0.623 0.627 α-Fe+(Vac-3H) 0.361 0.211 α-Fe+(Vac-4H) 0.322 –0.011 α-Fe+(Vac-5H) 0.227 –0.297 α-Fe+(Vac-6H) –0.028 –0.772
下载: 导出CSV
表 8 α-Fe+(nH-Vac)晶体原子轨道布居
Table 8. Atomic orbital population of α-Fe+(nH-Vac).
晶体类型 原子 轨道电荷占据数 总布居 净布居 s p d α-Fe+Vac Fe7, Fe11, Fe13 0.74 0.72 6.68 8.13 –0.13 Fe3, Fe5, Fe9 0.68 0.73 6.63 8.04 –0.04 其余Fe原子 0.66 0.67 6.60 7.93 0.07 α-Fe+(Vac-2H) Fe13 0.71 0.71 6.73 8.15 –0.15 Fe9 0.66 0.70 6.62 7.98 0.02 Fe11 0.71 0.71 6.65 8.07 –0.07 α-Fe+Vac—α-Fe+(Vac-6H) H1 1.20—1.22 0 0 1.20—1.22 –0.20— –0.22 自由态 H 1.00 0 0 1.00 0
下载: 导出CSV
表 9 α-Fe+Vac+H(T-site)的结合能、形成能和溶解热
Table 9. Binding energy, formation energy, and heat of solution of α-Fe+Vac+H(T-site).
晶体类型 ${E_{{\rm{crystal}}}}$/eV ${E_{{\rm{ZP}}}}$/eV ${E_{{\rm{bind}}}}$/eV $E_{{\rm{form}}}$/eV $\Delta H_{{ {\rm{sol} } } }^{\rm{H} }$/eV α–Fe+Vac+H(T-site) –12993.354 — –12993.353 0.248—0.250 5.012 2.755—2.756 0.339—0.340
下载: 导出CSV
-
[1] 张文钺 1999 焊接冶金学(基本原理)(北京: 机械工业出版社) 第241—244页
Zhang W Y 2012 Welding Metallurgy (Fundamental Principle) (Beijing: China Machine Press) pp241–244 (in Chinese)
[2] 张敬强 2015 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Zhang J Q 2015 Ph.D Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[3] Tateyama Y, Ohno T 2003 ISIJ Internation 43 573
Google Scholar
[4] Geng W T, Wan L, Du J P, Ogata S 2017 Scripta Materialia 134 105
Google Scholar
[5] MonasterioP R, Lau T T, Yip S, van Vliet K J 2009 Phys. Rev. Lett. 103 085501
Google Scholar
[6] Nagumo M, Nakamura M, Taika K 2001 Metall. Mater. Trans. A 32 339
Google Scholar
[7] Först C J, Slycke J, van Vliet K J, Yip S 2006 Phys. Rev. Lett. 96 175501
Google Scholar
[8] Fukai Y 1983 Jpn. J. Appl. Phys. 22 207
Google Scholar
[9] 张凤春, 李春福, 文平, 罗强, 冉曾令 2014 63 227101
Google Scholar
ZhangF C, Li C F, Wen P, Luo Q, Ran Z L 2014 Acta Phys. Sin. 63 227101
Google Scholar
[10] Du Y A, Ismer L, Rogal J, Hickel T, Neugebauer J, Drautz R 2011 Phys. Rev. B 84 144121
Google Scholar
[11] Nazarov R, Hickel T, Neugebauer J 2014 Phys. Rev. B 89 144108
Google Scholar
[12] Nazarov R, Hickel T, Neugebauer J 2012 Phys. Rev. B 85 144118
Google Scholar
[13] Hickel T, Grabowski B, Körmann F, Neugebauer J 2011 J. Phys. Condens. Mater. 24 053202
Google Scholar
[14] Ramasubramaniam A, Itakura M, Carter EA 2009 Phys. Rev. B 79 174101
Google Scholar
[15] Payne M C, Teter M P, Allan D C, Arias T A, Joannopoulos J D 1992 Rev. Mod. Phys. 64 1045
Google Scholar
[16] Milman V, Winkler B, White JA, Pickard C J, Payne M C, Akhmataskaya E V, Nobes R H 2000 Int. J. Quantum Chem. 77 895
Google Scholar
[17] Perdew JP, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[18] Methfessel M, Paxton A T 1989 Phys. Rev. B 40 3616
Google Scholar
[19] Acet M, Zähres H, Wassermann E F, Pepperhoff W 1994 Phys. Rev. B 49 6012
Google Scholar
[20] Hayward E, Fu C C 2013 Phys. Rev. B 87 174103
Google Scholar
[21] Baroni S, de Gironcoli S, Dal Corso A C, Giannozzi P 2001 Rev. Mod. Phys. 73 515
Google Scholar
[22] Bozzolo G, Ferrante J 1992 Phys. Rev. B 46 8600
Google Scholar
[23] Bhatia M A, Groh S, Solanki K N 2014 J. Appl. Phys. 116 064302
Google Scholar
[24] Tateyama Y, Ohno T 2003 Phys. Rev. B 67 174105
Google Scholar
[25] Mclellan R B, Harkins C G 1975 Mater. Sci. Eng. 18 5
Google Scholar
[26] Lynch SP 2013 Metall. Mater. Trans. A 44 1209
Google Scholar
[27] Lu G, Kaxiras E 2005 Phys. Rev. Lett. 94 155501
Google Scholar
[28] Ismer L, Hickel T, Neugebauer J 2010 Phys. Rev. B 81 094111
Google Scholar
[29] Korzhavyi P A, Abrikosov I A, Johansson B, Ruban A V, Skriver H L 1999 Phys. Rev. B 59 11693
Google Scholar
[30] Nazarov R, Hickel T, Neugebauer J 2010 Phys. Rev. B 82 224104
Google Scholar
[31] Speight J G 2005 Lange’s Handbook of Chemistry (16th Ed.) (New York: The McGraw-Hill Companies, Inc) pp1299−1309
下载:
计量
- 文章访问数: 8642
- PDF下载量: 139
- 被引次数: 0
