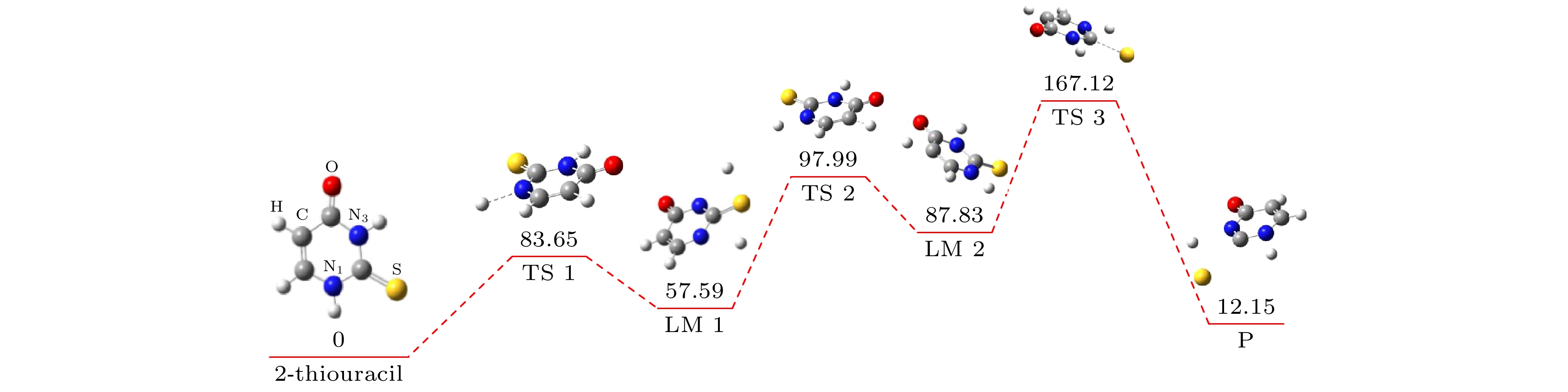
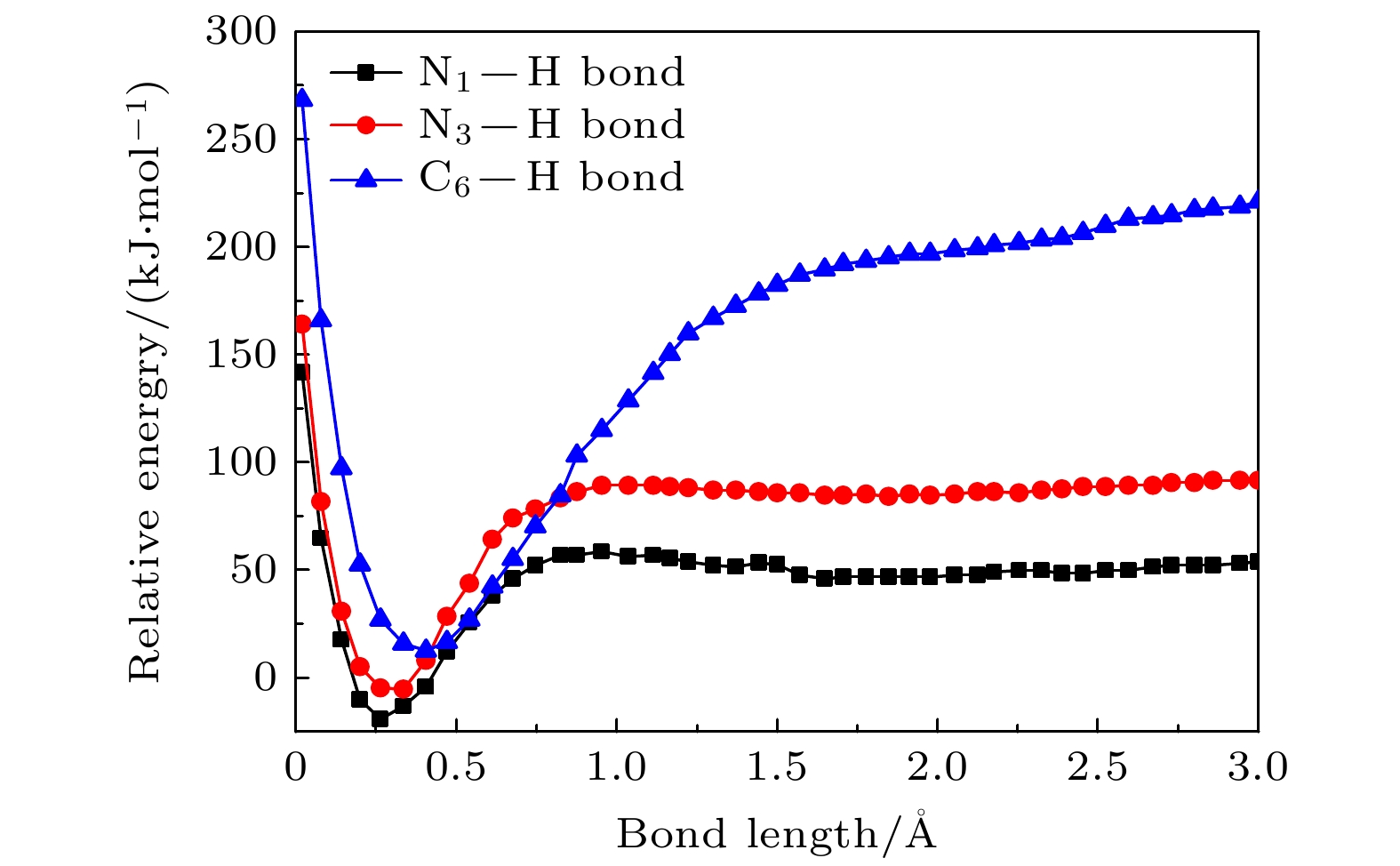
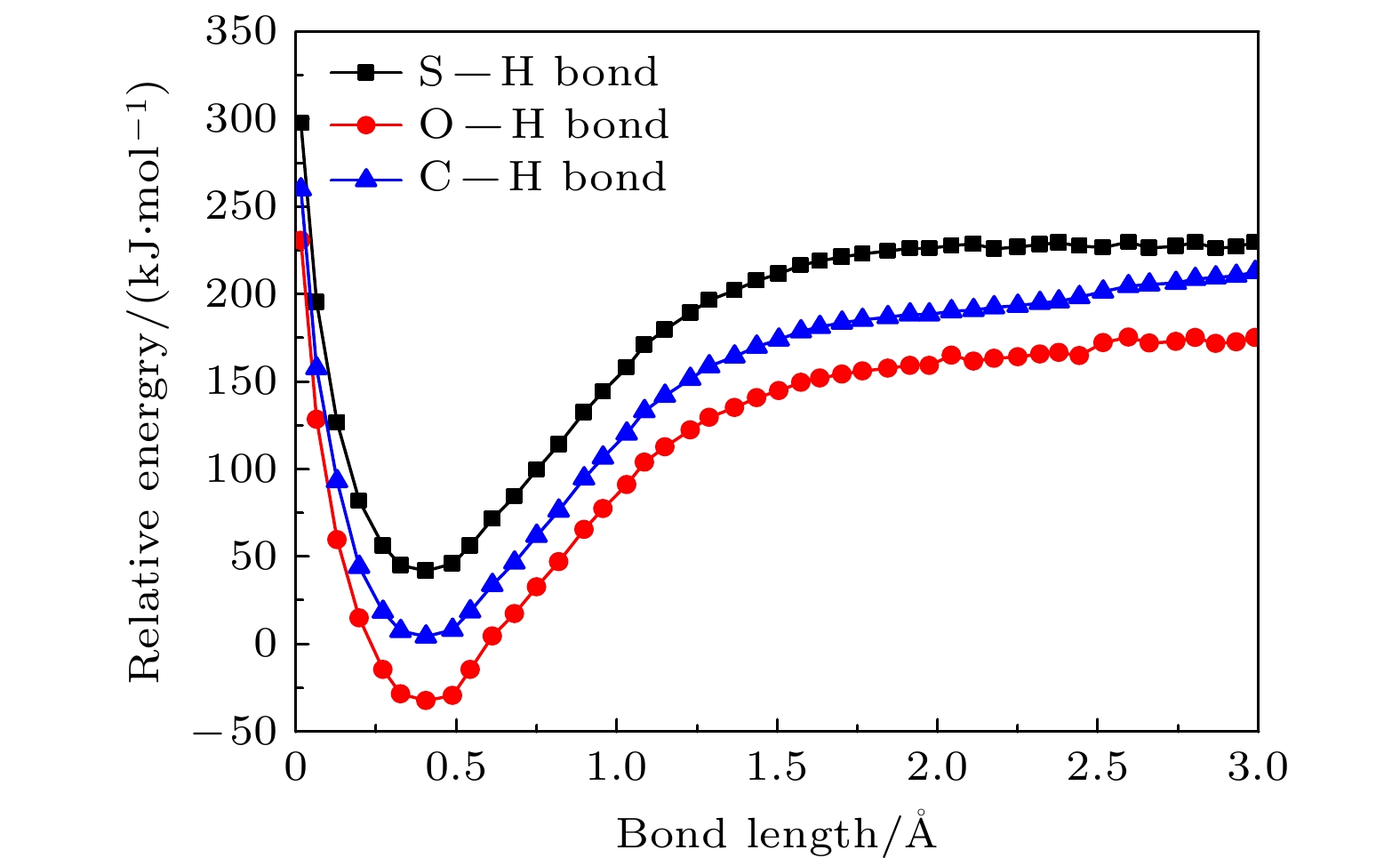
-
运用玻恩-奥本海默分子动力学模型结合密度泛函理论研究了气相下硫脲嘧啶与低能电子吸附解离动力学过程, 发现硫脲嘧啶及其互变异构体在吸附解离过程中一个重要的脱氢现象, 即特定位置的化学键N—H键, C—H键断裂, 使其在N位点和C位点失去氢原子, 形成解离过程中最主要的负离子碎片——闭壳层脱氢负离子(TU-H)–. 为了更深刻地认识脱氢现象, 分别对断裂的化学键进行势能曲线扫描, 对键解离能、电子亲和能、负离子(TU-H)–出现势进行计算对比发现, 在所有断裂的化学键中N—H键最容易发生断裂, 而负离子(TU-H)–的形成主要源于N—H键的断裂.
-
关键词:
- 玻恩-奥本海默分子动力学 /
- 密度泛函理论 /
- 电子吸附解离 /
- 硫脲嘧啶
When biomolecules interact with high-energy particles and rays, they are directly ionized or dissociated, then a large number of low-energy electrons are formed as secondary particles. These low-energy electrons will attach to biomolecules, and trigger off the secondary dissociation, forming free radicals and ions with high reactivity, which can damage the structure and function of the biomolecule and cause irreversible radiation damage to the biomolecule. It is important to study the low-energy dissociative electron attachment (DEA) process of biomolecules for understanding radiation damage to biological organisms. Currently, the theoretical studies of DEA have mainly focused on the bound states of negative ions and the types of resonances in the dissociation process. The dissociation process is well described by quantum computational method, but the diversity and complexity of dissociation channels present in the dissociation process of 2-thiouracil molecule also pose a great computational challenge to these methods. In addition, the quantum computational methods are not ideal for dealing with the discrete states of chemical bonds and the problem of continuity coupling of electrons. The dissociation dynamics of biomolecules mainly results from ionization and electron attachment. Ab initio molecular dynamics simulation can reasonably describe these processes. In light of these considerations, ab initio molecular dynamics simulation is used in this work to study dynamic variation process in DEA. The low-energy electron dissociative attachment to 2-thiouracil in the gas phase is studied by using the Born-Oppenheimer molecular dynamics model combined with density functional theory. It is found that an important dehydrogenation phenomenon of 2-thiouracil and its tautomers occurs in the DEA process, and that the N—H and C—H bond are broken at specific locations. Due to the loss of hydrogen atoms at the N and C sites, the closed-shell dehydrogenated negative ion (TU-H)– forms, which is the most important negative ion fragments in the dissociation process. The potential energy curves, the bond dissociation energy and the electron affinity energy of the broken bond show that the N—H bond is the most likely to break, indicating the formation of the negative ion (TU-H)– mainly comes from the breaking of N—H bond. The theoretical calculations in this work are in good agreement with the available experimental results, indicating that the chosen calculation method is fully reliable. The BOMD simulations can not only dynamically recover the process of dissociative attachment of low-energy electrons to 2-thiouracil, but also more importantly provide an insight into the mechanisms of dehydrogenation and dissociation channels of 2-thiouracil molecules in DEA process.-
Keywords:
- Born-Oppenheimer molecular dynamics /
- density functional theory /
- dissociative electron attachment /
- 2-thiouracil
[1] Gu B, Zhang F S, Wang Z P, Zhou H Y 2008 Phys. Rev. Lett. 100 088104
Google Scholar
[2] Zheng Y, Darel J. H, Ayotte P, Sanche L 2008 Phys. Rev. Lett. 100 168101
Google Scholar
[3] Zheng Y, Sanche L 2013 Rev. Nanosci. Nanotechnol. 2 1
Google Scholar
[4] Hou Q, Wang Y G 2001 Phys. Rev. Lett. 87 168101
Google Scholar
[5] Cimino R, Collins I R, Furman M A, Pivi M, Ruggiero F, Rumolo G, Zimmermann F 2004 Phys. Rev. Lett. 93 014801
Google Scholar
[6] Boudaı̈ffa B, Cloutier P, Hunting D, Huels M A, Sanche L 2000 Science 287 1658
Google Scholar
[7] Martin F, Burrow P D, Cai Z L, Cloutier P, Hunting D, Sanche L 2004 Phys. Rev. Lett. 93 068101
Google Scholar
[8] Christophorou L G 1978 Adv. Electron. Electron Phys. 46 55
[9] Elion G B 1989 Science 244 41.
Google Scholar
[10] 吕杰, 程静, 侯晓蓓 2016 生物医用材料导论 (上海: 同济大学出版社) 第86页
Lyu J, Cheng J, Hou X L 2016 An Introduction to Biomedical Materials (Shanghai: Tongji University Press) p86
[11] Kopyra J, Kopyra K K, Abdoul-Carime H, Branowska D 2018 J. Chem. Phys. 148 234301
Google Scholar
[12] Maio N, Lafont B A P, Sil D, Li Y, Martin Bollinger Jr J, Krebs C, Pierson C, Linehan W, Rouault T A 2021 Science 373 6651
[13] Ruckenbauer M, Mai S, Marquetand P, Gonzálezb L 2016 J. Chem. Phys. 144 074303
Google Scholar
[14] Uleanya K O, Dessent C E H 2021 Phys. Chem. Chem. Phys. 23 1021
Google Scholar
[15] Fennimorea M A, Matsika S 2016 Phys. Chem. Chem. Phys. 44 30536
[16] Puzzarini C, Biczysko M, Barone V, Peña I, Cabezas C, Alonso J L 2013 Phys. Chem. Chem. Phys. 39 16965
[17] Plekan O, Feyer V, Cassidy A, Lyamayev V, Tsud N, Ptasińska S, Reiff S, Acres R G, Princeag K C 2015 Phys. Chem. Chem. Phys. 17 15181
Google Scholar
[18] Kopyra J, Abdoul-Carime H, Kossoskic F, Varella M T 2014 Phys. Chem. Chem. Phys. 14 25054
[19] Kopyra J, Kopyra K K, Abdoul-Carime H, Branowska D 2016 J. Chem. Phys. 144 034306
Google Scholar
[20] Dolgounitcheva O, Zakrzewski V G, Ortiz J V 2011 J. Chem. Phys. 134 074305
Google Scholar
[21] Da Costa R F, Varella M T, Lima M A P, Bettega M H F 2013 J. Chem. Phys. 138 194306
Google Scholar
[22] Kossoski F, Bettega M H F, Varella M T 2014 J. Chem. Phys. 140 024317
Google Scholar
[23] Yang H J, Wang E L, Dong W X, Gong M M, Shen Z J, Tang Y G, Shan X, Chen X J 2018 Phys. Rev. A 97 052703
Google Scholar
[24] Feng W L, Tian S X 2015 J. Phys. Chem. A 119 1838
Google Scholar
[25] Wang Y F, Tian S X, Yang J 2011 Phys. Chem. Chem. Phys. 13 15597
Google Scholar
[26] 冯文玲 2015 博士学位论文 (合肥: 中国科学技术大学)
Feng W L 2015 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[27] López-Tarifa P, Hervé du Penhoat M A, Vuilleumier R, Gaigeot M P, Tavernelli I, Padellec A L, Champeaux J P, Alcamí M, Moretto-Capelle P, Martín F, Politis M F 2011 Phys. Rev. Lett. 107 023202
Google Scholar
[28] Boys S F, Bernardi F 1970 Mol. Phys. 19 553
Google Scholar
-
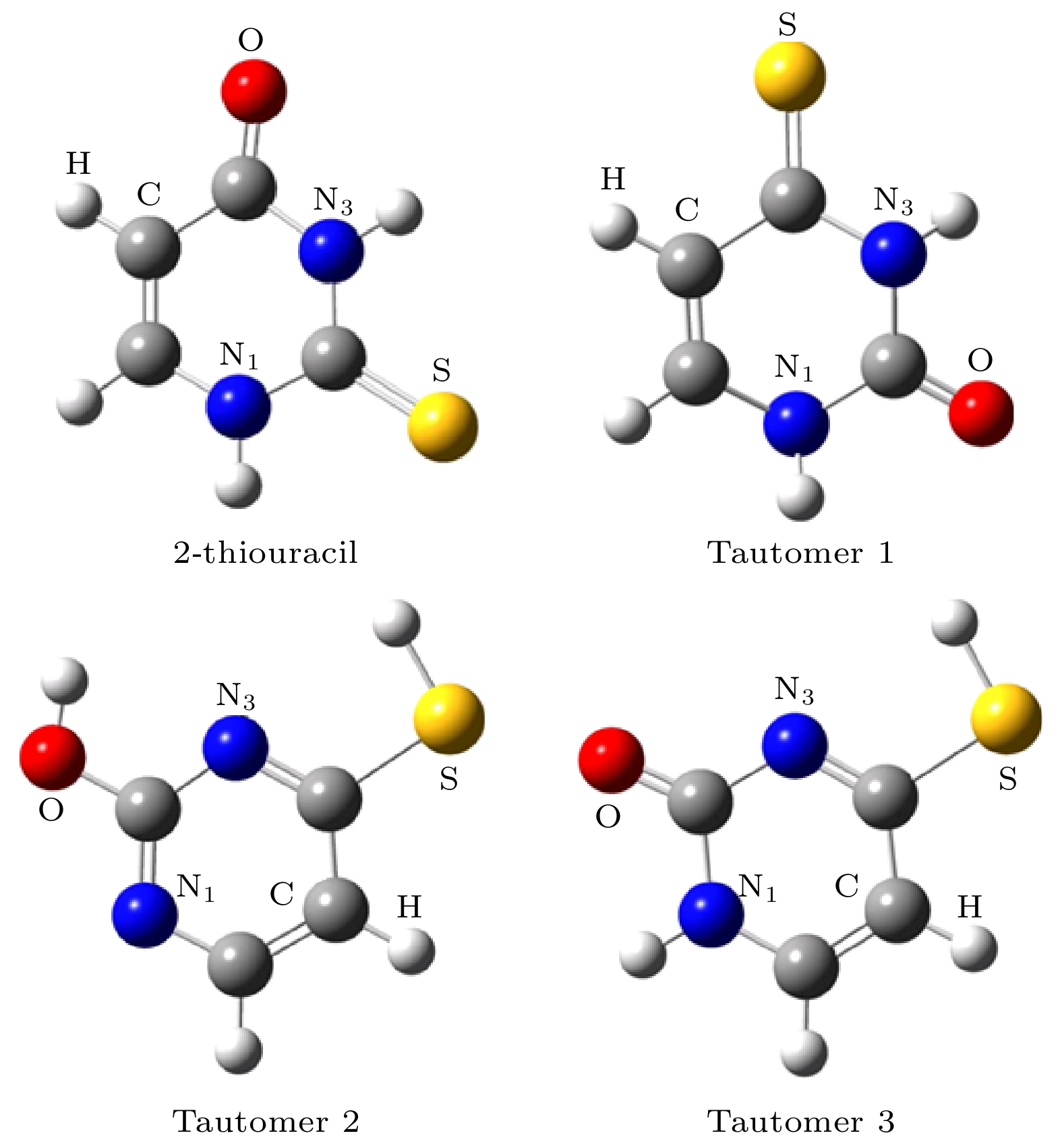
图 1 采用B3LYP/6-311++G(2d, 2p)方法优化后基态硫脲嘧啶分子及其互变异构体的几何构型 (图中红色为氧原子, 白色为氢原子, 灰色为碳原子, 蓝色为氮原子, 黄色为硫原子)
Fig. 1. Optimized geometries of the ground state 2-thiouracil and its tautomers. The geometries have been optimized using the B3LYP method and the 6-311++G(2d, 2p) basis set (Colors in graphical representations correspond to atom types as follows, red: oxygen; white: hydrogen; gray: carbon; blue: nitrogen; yellow: sulfur).
图 2 硫脲嘧啶及其互变异构体1在解离过程中分子结构随时间演化图
Fig. 2. The evolution of the geometrical structures of 2-thiouracil and tautomer 1 during dissociation.
图 3 硫脲嘧啶互变异构体2和其互变异构体3在解离过程中分子结构随时间演化图
Fig. 3. The evolution of the geometrical structures of tautomer 2 and tautomer 3 during dissociation.
图 4 硫脲嘧啶解离过程势能剖面示意图
Fig. 4. The potential energy profile of the 2-thiouracil dissociation.
图 5 B3LYP/6-311++G(2d, 2p)方法计算获得硫脲嘧啶解离过程中化学键N—H键和C—H键的势能曲线
Fig. 5. The potential energy curves for the N—H and the C—H bond in 2-thiouracil dissociation obtained from B3LYP/6-311++G(2d, 2p) calculations.
图 6 硫脲嘧啶互变异构体2解离过程势能剖面示意图
Fig. 6. The potential energy profile of the tautomer 2 dissociation.
图 7 B3LYP/6-311++G(2d, 2p)方法计算获得硫脲嘧啶互变异构体2解离过程中化学键C—H键、O—H键和S—H键的势能曲线
Fig. 7. The potential energy curves for the C—H , the O—H and the S—H bond in tautomer 2 dissociation obtained from B3LYP/6-311++G(2d, 2p) calculations.
图 8 B3LYP/6-311++ G(2d, 2p)方法计算获得硫脲嘧啶互变异构体3解离过程化学键N1—H键的势能曲线
Fig. 8. The potential energy curves for the N1—H bond in tautomer 3 dissociation obtained from B3LYP/6-311++G(2d, 2p) calculations.
表 1 硫脲嘧啶分子及其互变异构体稳定构型的相对能量, 基组重叠误差BSSE, CP校正后的结合能$ \Delta {E}_{{\mathrm{C}}{\mathrm{P}}} $ 和偶极矩μ
Table 1. Relative energies, BSSE, CP-corrected binding energies $ \Delta {E}_{{\mathrm{C}}{\mathrm{P}}} $ and dipole moment of 2-thiouracil and its tautomers.
Method 2-thiouracil Tautomer 1 Tautomer 2 Tautomer 3 CCSD/6-311++G(2d, 2p) 0 46.31 93.59 70.43 MP2/6-311++G(2d, 2p) 0 30.88 61.75 50.17 B3LYP/6-31G(d) [18] 0 221.92 238.32 222.88 CCSD(T)/Aug-cc-pVDZ[18] 0 48.24 94.56 76.22 BSSE 0.54 0.43 0.61 0.49 $ \Delta {E}_{{\mathrm{C}}{\mathrm{P}}} $/(kJ·mol–1) –18.37 –18.44 –22.33 –33.63 μ/Debye 5.13 5.12 4.66 4.92 
下载: 导出CSV
表 2 由CCSD计算方法获得硫脲嘧啶及其互变异构体分子不同位置脱氢所需的键解离能, 绝热电子亲和能和(TU-H)–负离子出现势(能量单位为kJ/mol)
Table 2. The bond dissociation energy, the adiabatic electron affinity and the appearance potential of the (TU-H)– obtained from CCSD calculation method of dehydrogenation of 2-thiouracil and its tautomer at different positions (all values in kJ/mol)
Bond BE EA AE 2-thiouracil N1—H 58.86 3630.73 2047.41 N3—H 108.06 5957.95 46.31 C—H 378.22 213.23 164.99 Tautomer 1 N1—H 59.82 40.52 19.3 N3—H 109.03 56.93 52.1 C—H 382.08 218.05 164.02 Tautomer 2 O—H 198.76 116.75 178.5 S—H 418.74 187.18 231.56 C—H 343.48 222.88 165.95 Tautomer 3 N1—H 165.95 60.79 105.17 C—H 384.98 224.81 160.17 S—H 420.67 190.08 230.6
下载: 导出CSV
表 3 由CCSD计算方法获得硫脲嘧啶及其互变异构体解离通道(6)式和(7)式所需的最小解离能(能量单位为kJ/mol).
Table 3. The minimum dissociation energy required to obtain 2-thiouracil and its tautomer dissociation channels (6) and (7) by CCSD calculation method (all values in kJ/mol).
Bond $ E_{({\rm TU}-2{\rm H})^- + {\rm H} + {\rm H}} $ $ E_{\rm(TU-H_2)^- + H_2}$ 2-thiouracil N1—HN3—H 591.45 88.77 N1—HC—H 526.81 147.62 N3—HC—H 584.7 156.3 Tautomer 1 N1—HN3—H 597.24 91.66 N1—HC—H 528.74 160.17 N3—HC—H 591.45 162.09 Tautomer 2 O—HS—H 551.89 237.35 O—HC—H 446.73 189.11 S—HC—H 630.05 344.45 Tautomer 3 N1—HC—H 604.96 166.92 N1—HS—H 640.66 329.01 C—HS—H 651.27 362.78
下载: 导出CSV
-
[1] Gu B, Zhang F S, Wang Z P, Zhou H Y 2008 Phys. Rev. Lett. 100 088104
Google Scholar
[2] Zheng Y, Darel J. H, Ayotte P, Sanche L 2008 Phys. Rev. Lett. 100 168101
Google Scholar
[3] Zheng Y, Sanche L 2013 Rev. Nanosci. Nanotechnol. 2 1
Google Scholar
[4] Hou Q, Wang Y G 2001 Phys. Rev. Lett. 87 168101
Google Scholar
[5] Cimino R, Collins I R, Furman M A, Pivi M, Ruggiero F, Rumolo G, Zimmermann F 2004 Phys. Rev. Lett. 93 014801
Google Scholar
[6] Boudaı̈ffa B, Cloutier P, Hunting D, Huels M A, Sanche L 2000 Science 287 1658
Google Scholar
[7] Martin F, Burrow P D, Cai Z L, Cloutier P, Hunting D, Sanche L 2004 Phys. Rev. Lett. 93 068101
Google Scholar
[8] Christophorou L G 1978 Adv. Electron. Electron Phys. 46 55
[9] Elion G B 1989 Science 244 41.
Google Scholar
[10] 吕杰, 程静, 侯晓蓓 2016 生物医用材料导论 (上海: 同济大学出版社) 第86页
Lyu J, Cheng J, Hou X L 2016 An Introduction to Biomedical Materials (Shanghai: Tongji University Press) p86
[11] Kopyra J, Kopyra K K, Abdoul-Carime H, Branowska D 2018 J. Chem. Phys. 148 234301
Google Scholar
[12] Maio N, Lafont B A P, Sil D, Li Y, Martin Bollinger Jr J, Krebs C, Pierson C, Linehan W, Rouault T A 2021 Science 373 6651
[13] Ruckenbauer M, Mai S, Marquetand P, Gonzálezb L 2016 J. Chem. Phys. 144 074303
Google Scholar
[14] Uleanya K O, Dessent C E H 2021 Phys. Chem. Chem. Phys. 23 1021
Google Scholar
[15] Fennimorea M A, Matsika S 2016 Phys. Chem. Chem. Phys. 44 30536
[16] Puzzarini C, Biczysko M, Barone V, Peña I, Cabezas C, Alonso J L 2013 Phys. Chem. Chem. Phys. 39 16965
[17] Plekan O, Feyer V, Cassidy A, Lyamayev V, Tsud N, Ptasińska S, Reiff S, Acres R G, Princeag K C 2015 Phys. Chem. Chem. Phys. 17 15181
Google Scholar
[18] Kopyra J, Abdoul-Carime H, Kossoskic F, Varella M T 2014 Phys. Chem. Chem. Phys. 14 25054
[19] Kopyra J, Kopyra K K, Abdoul-Carime H, Branowska D 2016 J. Chem. Phys. 144 034306
Google Scholar
[20] Dolgounitcheva O, Zakrzewski V G, Ortiz J V 2011 J. Chem. Phys. 134 074305
Google Scholar
[21] Da Costa R F, Varella M T, Lima M A P, Bettega M H F 2013 J. Chem. Phys. 138 194306
Google Scholar
[22] Kossoski F, Bettega M H F, Varella M T 2014 J. Chem. Phys. 140 024317
Google Scholar
[23] Yang H J, Wang E L, Dong W X, Gong M M, Shen Z J, Tang Y G, Shan X, Chen X J 2018 Phys. Rev. A 97 052703
Google Scholar
[24] Feng W L, Tian S X 2015 J. Phys. Chem. A 119 1838
Google Scholar
[25] Wang Y F, Tian S X, Yang J 2011 Phys. Chem. Chem. Phys. 13 15597
Google Scholar
[26] 冯文玲 2015 博士学位论文 (合肥: 中国科学技术大学)
Feng W L 2015 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[27] López-Tarifa P, Hervé du Penhoat M A, Vuilleumier R, Gaigeot M P, Tavernelli I, Padellec A L, Champeaux J P, Alcamí M, Moretto-Capelle P, Martín F, Politis M F 2011 Phys. Rev. Lett. 107 023202
Google Scholar
[28] Boys S F, Bernardi F 1970 Mol. Phys. 19 553
Google Scholar
下载:
计量
- 文章访问数: 2067
- PDF下载量: 54
- 被引次数: 0
