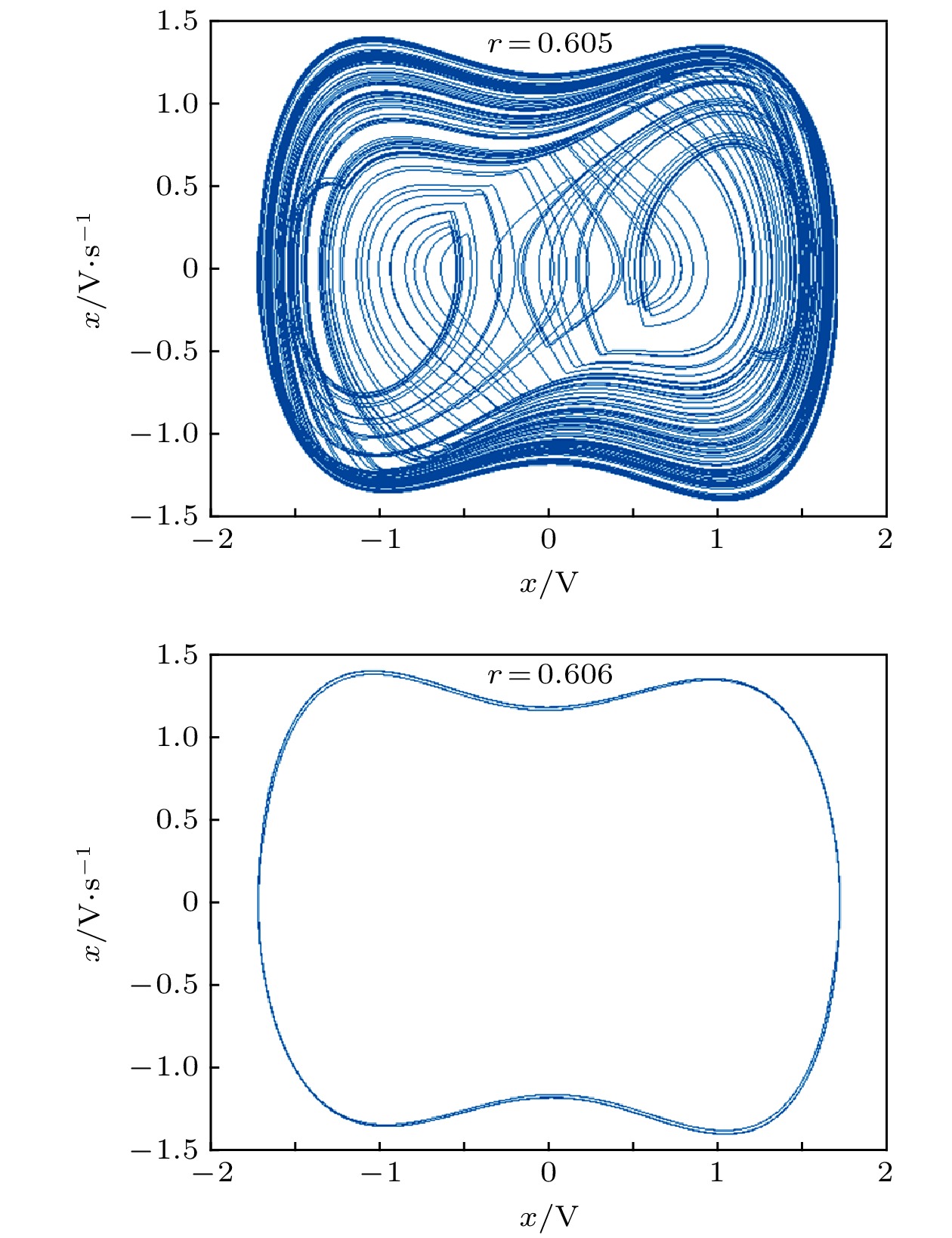
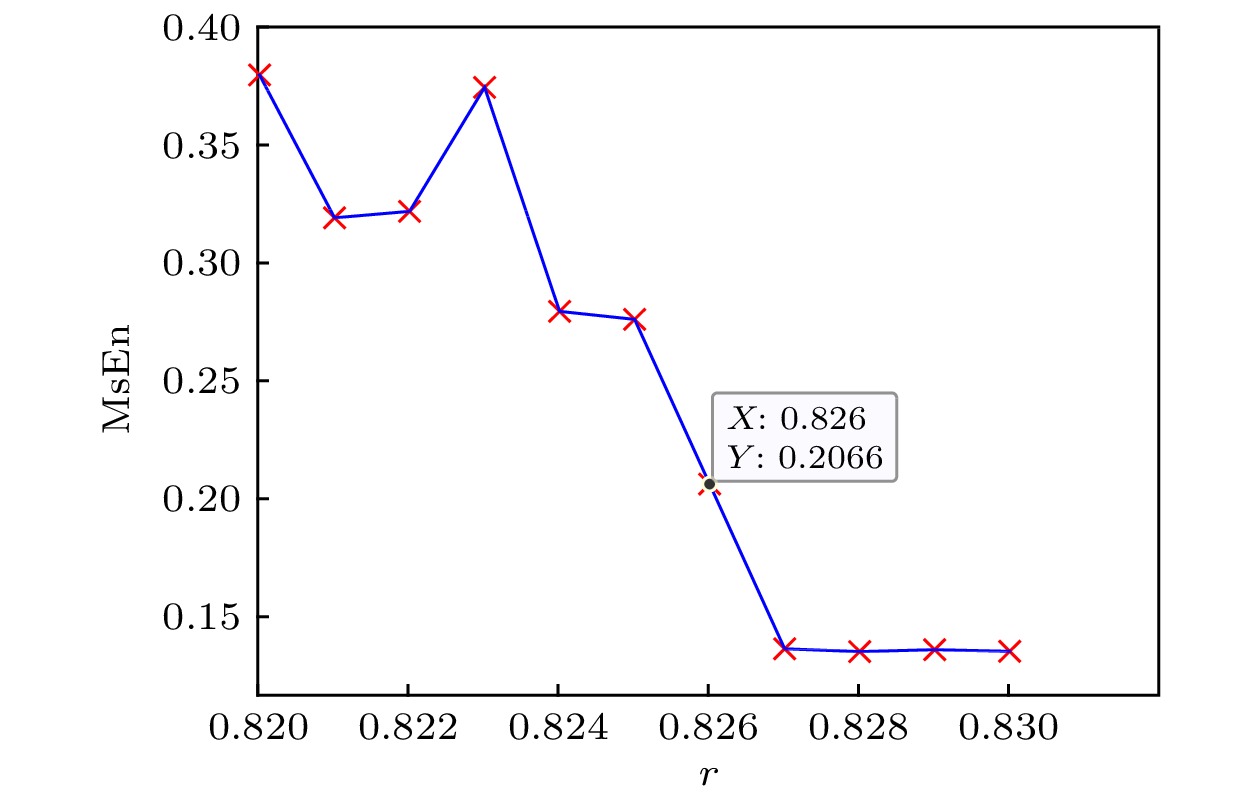
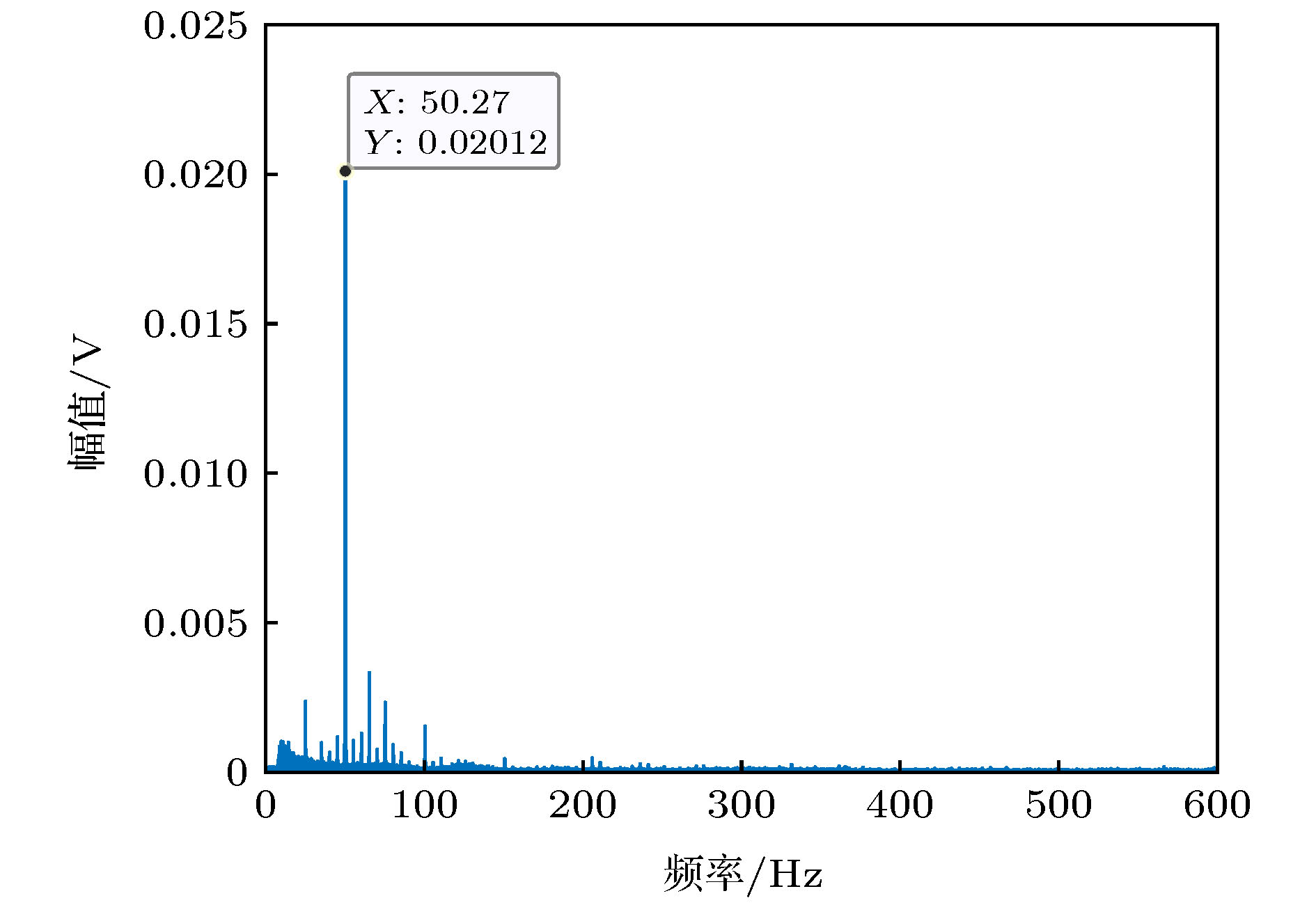
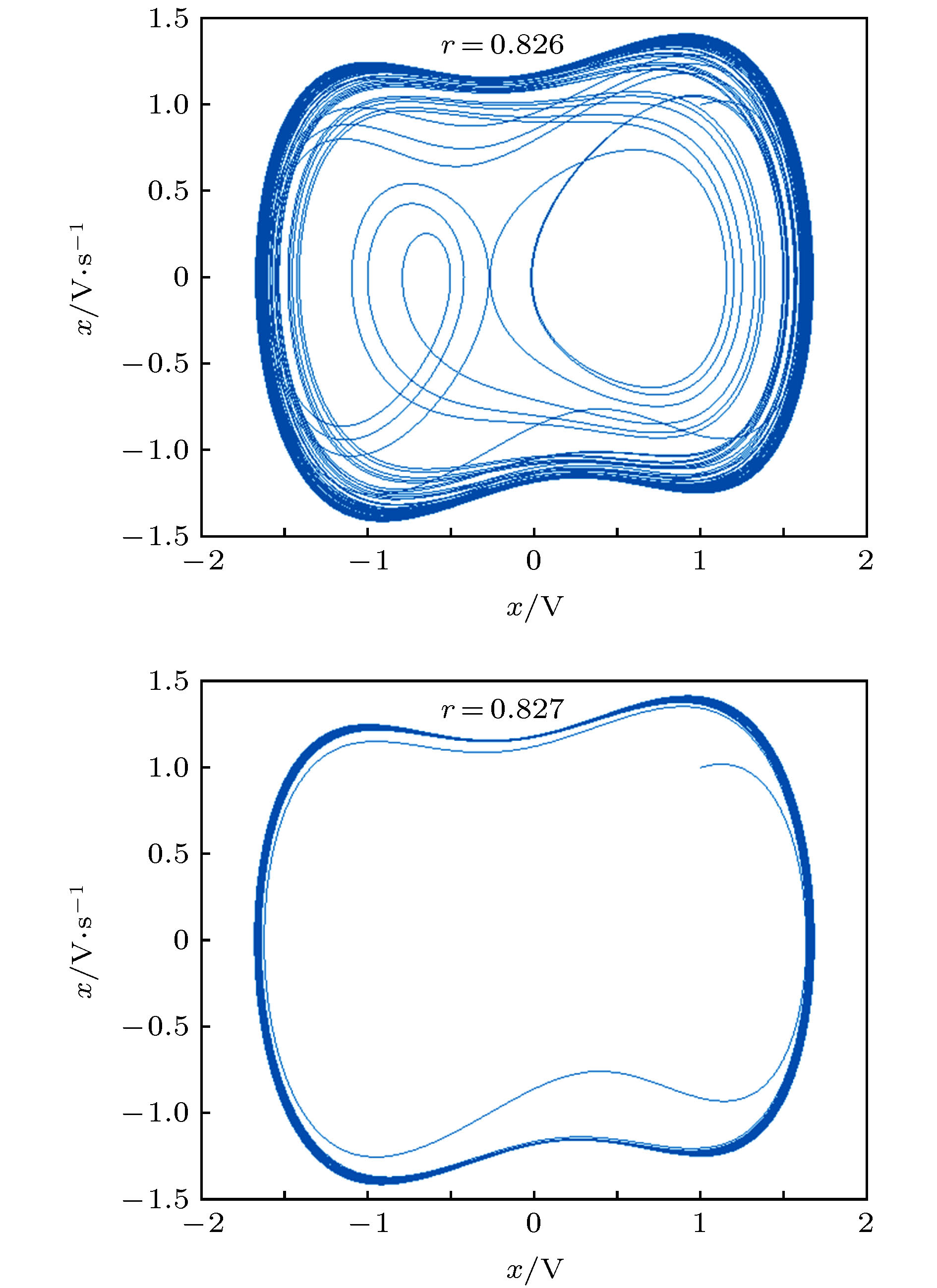
-
熵是热力学中表征物质状态的参量之一, 是体系混乱程度的度量. 一个信号的熵可以用来表示信号的复杂度. Duffing混沌系统从临界混沌状态向大尺度周期状态跃变的阈值是混沌系统分析的一个重要参数, 它的求解方法是混沌理论目前亟待解决的问题之一. 然而传统的实验分析法或者定量分析法存在一定的局限性. 本文在研究中发现, 系统处于混沌态和周期态时输出的多尺度熵值存在较大差异, 且当系统进入周期态后多尺度熵值趋于平稳, 基于这一现象结合遗传算法提出了基于多尺度熵的Duffing混沌系统阈值确定方法. 利用该方法对正弦信号和方波信号的检测系统跃变阈值进行了计算, 结果表明该方法快速准确且计算简单.Entropy is one of the parameters describing the state of matter in thermodynamics, it can be used to measure the degree of confusion. The entropy of the signal can be used to express the complexity of the signal. The threshold for the transition of the Duffing chaotic system from the critical chaotic state to the large-scale periodic state is called the transition threshold. It is an important parameter for the analysis of chaotic systems, and its solution method is one of the problems urgently to be solved in chaos theory. If the jump threshold is smaller than the real threshold of the system, it will affect its detection signal-to-noise ratio. If the jump threshold is larger than the real threshold, it will cause incorrect detection results, so it is very important to accurately determine the jump threshold. In this study, we found that the multiscale sample entropy value of the Duffing system is significantly different when the system is in the chaotic state and the periodic state, when the system is in a chaotic state, the entropy value is larger, when the system is in a periodic state, the entropy value is smaller, and when the system enters the periodic state, the multiscale entropy value tends to be stable, this paper proposes to use this phenomenon to determine the transition threshold by analyzing the relationship between the entropy of the system and the amplitude of the driving force. When the entropy value is obviously smaller and tends to be stable, the corresponding driving force amplitude is the jump threshold. using this method, the jump threshold of the sinusoidal signal and square wave signal detection system is calculated, the results show that the method is fast, accurate and simple to calculate. However, this method may have a problem that the calculated threshold value is smaller than the real threshold value, our analysis is that the random selection of the subsequence used for calculation causes the calculation threshold value to be too small, so the method is improved in conjunction with genetic algorithm, using genetic algorithm to find the most complicated subsequence in the whole sequence, then this subsequence is used to solve the threshold, Through a large number of calculations and analysis, it can be seen that the problem of a small threshold is no longer present, and the improved method can obtain the jump threshold of the Duffing system very accurately.
[1] 王冠宇, 陶国良, 陈行, 林建亚 1997 仪器仪表学报 18 98
Wang G Y, Tao G L, Chen X, Lin J Y 1997 Chinese Journal Of Scientific Instrument 18 98
[2] 李月, 杨宝俊, 石要武, 张忠彬, 于功梅 2001 吉林大学自然科学学报 1 75
Li Y, Yang B J, Shi Y W, Zhang Z B, Yu G M 2001 Acta Scientiarum Naturalium Universitatis JiLinensis 1 75
[3] 李月, 杨宝俊, 石要武, 张忠彬, 于功梅 2001 吉林大学自然科学学报 2 65
Li Y, Yang B J, Shi Y W, Zhang Z B, Yu G M 2001 Acta Scientiarum Naturalium Universitatis JiLinensis 2 65
[4] 李月, 杨宝俊, 石要武 2003 52 526
Google Scholar
Li Y, Yang B J, Shi Y W 2003 Acta Phys. Sin. 52 526
Google Scholar
[5] 李月, 路鹏, 杨宝俊, 赵雪平 2006 55 1672
Google Scholar
Li Y, Lu P, Yang B J, Zhao X P 2006 Acta Phys. Sin. 55 1672
Google Scholar
[6] 赖志慧, 冷永刚, 孙建桥, 范胜波 2012 61 050503
Google Scholar
Lai Z H, Leng Y G, Sun J Q, Fan S B 2012 Acta Phys. Sin. 61 050503
Google Scholar
[7] 丛超, 李秀坤, 宋扬 2014 63 064301
Google Scholar
Cong C, Li X K, Song Y 2014 Acta Phys. Sin. 63 064301
Google Scholar
[8] 牛德智, 陈长兴, 班斐, 徐浩翔, 李永宾, 王卓, 任晓岳, 陈强 2015 64 060503
Google Scholar
Niu D Z, Chen C X, Ban F, Xu H X, Li Y B, Wang Z, Ren X Y, Chen Q 2015 Acta Phys. Sin. 64 060503
Google Scholar
[9] 陈志光, 李亚安, 陈晓 2015 64 200502
Google Scholar
Chen Z G, Li Y A, Chen X 2015 Acta Phys. Sin. 64 200502
Google Scholar
[10] 时培明, 孙彦龙, 韩东颖 2016 计量学报 37 310
Google Scholar
Shi P M, Sun Y L, Han D Y 2016 Acta Metrologica Sinica 37 310
Google Scholar
[11] 高振斌, 孙月明, 李景春 2015 河北工业大学学报 44 23
Gao Z B, Sun Y M, Li J C 2015 Journal Of Hebei University of Technology 44 23
[12] 张菁, 王斌, 叶家敏 2016 实验室研究与探索 35 86
Google Scholar
Sun J, Wang B, Ye J M 2016 Research And Exploration In Laboratory 35 86
Google Scholar
[13] Gottwald G A, Melbourne I 2004 Physica D 212 100
[14] Gottwald G A, Melbourne I 2009 SIAM J. Appl. Dyn. Syst. 8 129
Google Scholar
[15] 蔺向阳, 陈长兴, 凌飞云, 黄继尧 2019 空军工程大学学报(自然科学版) 20 86
Lin X Y, Chen C X, Ling F Y, Huang J Y 2019 Journal of Air Force Engineering University(Natural Science Edition) 20 86
[16] 梁涤青, 陈志刚, 邓小鸿 2015 电子学报 43 1972
Liang D Q, Chen Z G, Deng X H 2015 Acta Electronica Sinica 43 1972
[17] 杨孝敬, 杨阳, 李淮周, 钟宁 2016 65 218701
Google Scholar
Yang X J, Yang y, Li H Z, Zhong N 2016 Acta Phys. Sin. 65 218701
Google Scholar
[18] 陈祥龙, 张兵志, 冯辅周, 江鹏程 2018 振动工程学报 31 902
Chen X L, Zhang B Z, Feng F Z, Jiang P C 2018 Journal of Vibration Engineering 31 902
[19] 王鸿姗, 周静雷, 房乔楚 2019 西安工程大学学报 32 57
Wang H S, Zhou J L, Fang Q C 2019 Journal of Xi’an Polytechnic University 32 57
[20] 徐为 2017 博士学位论文 (哈尔滨: 黑龙江大学)
Xu W 2017 Ph. D. Dissertation (Haerbin: HeiLongJiang University) (in Chinese)
-
图 1 系统状态跃变 (a) 临界混沌状态; (b) 周期状态
Fig. 1. System state transition: (a) System state transition; (b) periodic state.
图 2 方波信号检测系统多尺度熵变化情况
Fig. 2. Variation of multi-scale entropy in square wave signal detection system.
图 3 仿真实验求解方波信号检测系统阈值
Fig. 3. Simulation experiment to solve the threshold of square wave signal detection system.
图 4 正弦信号检测系统多尺度熵变化情况
Fig. 4. Variation of multi-scale entropy in sinusoidal signal detection system.
图 5 仿真实验求解正弦信号检测系统阈值
Fig. 5. Simulation experiment to solve the threshold of sinusoidal signal detection system.
图 8 真实信号检测系统多尺度熵值变化情况
Fig. 8. Changes in multi-scale entropy of real signal detection system.
图 9 仿真实验求解真实水声信号检测系统阈值
Fig. 9. Simulation experiment to solve the threshold of real underwater acoustic signal detection system.
图 10 对真实水声信号的检测 (a) 系统未添加真实信号; (b)系统添加真实信号
Fig. 10. Detecting real underwater acoustic signals: (a) The system did not add a real signal; (b) system adds real signal
图 11 5 rad/s正弦信号检测系统多尺度熵变化情况
Fig. 11. Variation of multi-scale entropy in 5 rad/s sinusoidal signal detection system.
图 12 仿真实验求解5 rad/s正弦信号检测系统跃变阈值
Fig. 12. Simulation experiment to solve the threshold of 5 rad/s sinusoidal signal detection system.
图 14 5 rad/s正弦信号检测系统最大多尺度熵变化情况
Fig. 14. Variation of maximum multi-scale entropy of 5 rad/s sinusoidal signal detection system.
表 1 Duffing子序列段熵值(
$r = 0.826$ )Table 1. Entropy value of the Duffing subsequence segment (
$r = 0.826$ )序列 1 2 3 4 5 6 MsEn 0.1188 0.0779 0.0768 0.0796 0.0766 0.0780 
下载: 导出CSV
表 2 Duffing子序列段MsEn值(
$r = 0.827$ )Table 2. Entropy value of the Duffing subsequence segment(
$r = 0.827$ )序列 1 2 3 4 5 6 MsEn 0.0820 0.0822 0.0802 0.0790 0.0777 0.0753
下载: 导出CSV
-
[1] 王冠宇, 陶国良, 陈行, 林建亚 1997 仪器仪表学报 18 98
Wang G Y, Tao G L, Chen X, Lin J Y 1997 Chinese Journal Of Scientific Instrument 18 98
[2] 李月, 杨宝俊, 石要武, 张忠彬, 于功梅 2001 吉林大学自然科学学报 1 75
Li Y, Yang B J, Shi Y W, Zhang Z B, Yu G M 2001 Acta Scientiarum Naturalium Universitatis JiLinensis 1 75
[3] 李月, 杨宝俊, 石要武, 张忠彬, 于功梅 2001 吉林大学自然科学学报 2 65
Li Y, Yang B J, Shi Y W, Zhang Z B, Yu G M 2001 Acta Scientiarum Naturalium Universitatis JiLinensis 2 65
[4] 李月, 杨宝俊, 石要武 2003 52 526
Google Scholar
Li Y, Yang B J, Shi Y W 2003 Acta Phys. Sin. 52 526
Google Scholar
[5] 李月, 路鹏, 杨宝俊, 赵雪平 2006 55 1672
Google Scholar
Li Y, Lu P, Yang B J, Zhao X P 2006 Acta Phys. Sin. 55 1672
Google Scholar
[6] 赖志慧, 冷永刚, 孙建桥, 范胜波 2012 61 050503
Google Scholar
Lai Z H, Leng Y G, Sun J Q, Fan S B 2012 Acta Phys. Sin. 61 050503
Google Scholar
[7] 丛超, 李秀坤, 宋扬 2014 63 064301
Google Scholar
Cong C, Li X K, Song Y 2014 Acta Phys. Sin. 63 064301
Google Scholar
[8] 牛德智, 陈长兴, 班斐, 徐浩翔, 李永宾, 王卓, 任晓岳, 陈强 2015 64 060503
Google Scholar
Niu D Z, Chen C X, Ban F, Xu H X, Li Y B, Wang Z, Ren X Y, Chen Q 2015 Acta Phys. Sin. 64 060503
Google Scholar
[9] 陈志光, 李亚安, 陈晓 2015 64 200502
Google Scholar
Chen Z G, Li Y A, Chen X 2015 Acta Phys. Sin. 64 200502
Google Scholar
[10] 时培明, 孙彦龙, 韩东颖 2016 计量学报 37 310
Google Scholar
Shi P M, Sun Y L, Han D Y 2016 Acta Metrologica Sinica 37 310
Google Scholar
[11] 高振斌, 孙月明, 李景春 2015 河北工业大学学报 44 23
Gao Z B, Sun Y M, Li J C 2015 Journal Of Hebei University of Technology 44 23
[12] 张菁, 王斌, 叶家敏 2016 实验室研究与探索 35 86
Google Scholar
Sun J, Wang B, Ye J M 2016 Research And Exploration In Laboratory 35 86
Google Scholar
[13] Gottwald G A, Melbourne I 2004 Physica D 212 100
[14] Gottwald G A, Melbourne I 2009 SIAM J. Appl. Dyn. Syst. 8 129
Google Scholar
[15] 蔺向阳, 陈长兴, 凌飞云, 黄继尧 2019 空军工程大学学报(自然科学版) 20 86
Lin X Y, Chen C X, Ling F Y, Huang J Y 2019 Journal of Air Force Engineering University(Natural Science Edition) 20 86
[16] 梁涤青, 陈志刚, 邓小鸿 2015 电子学报 43 1972
Liang D Q, Chen Z G, Deng X H 2015 Acta Electronica Sinica 43 1972
[17] 杨孝敬, 杨阳, 李淮周, 钟宁 2016 65 218701
Google Scholar
Yang X J, Yang y, Li H Z, Zhong N 2016 Acta Phys. Sin. 65 218701
Google Scholar
[18] 陈祥龙, 张兵志, 冯辅周, 江鹏程 2018 振动工程学报 31 902
Chen X L, Zhang B Z, Feng F Z, Jiang P C 2018 Journal of Vibration Engineering 31 902
[19] 王鸿姗, 周静雷, 房乔楚 2019 西安工程大学学报 32 57
Wang H S, Zhou J L, Fang Q C 2019 Journal of Xi’an Polytechnic University 32 57
[20] 徐为 2017 博士学位论文 (哈尔滨: 黑龙江大学)
Xu W 2017 Ph. D. Dissertation (Haerbin: HeiLongJiang University) (in Chinese)
下载:
计量
- 文章访问数: 8119
- PDF下载量: 157
- 被引次数: 0
