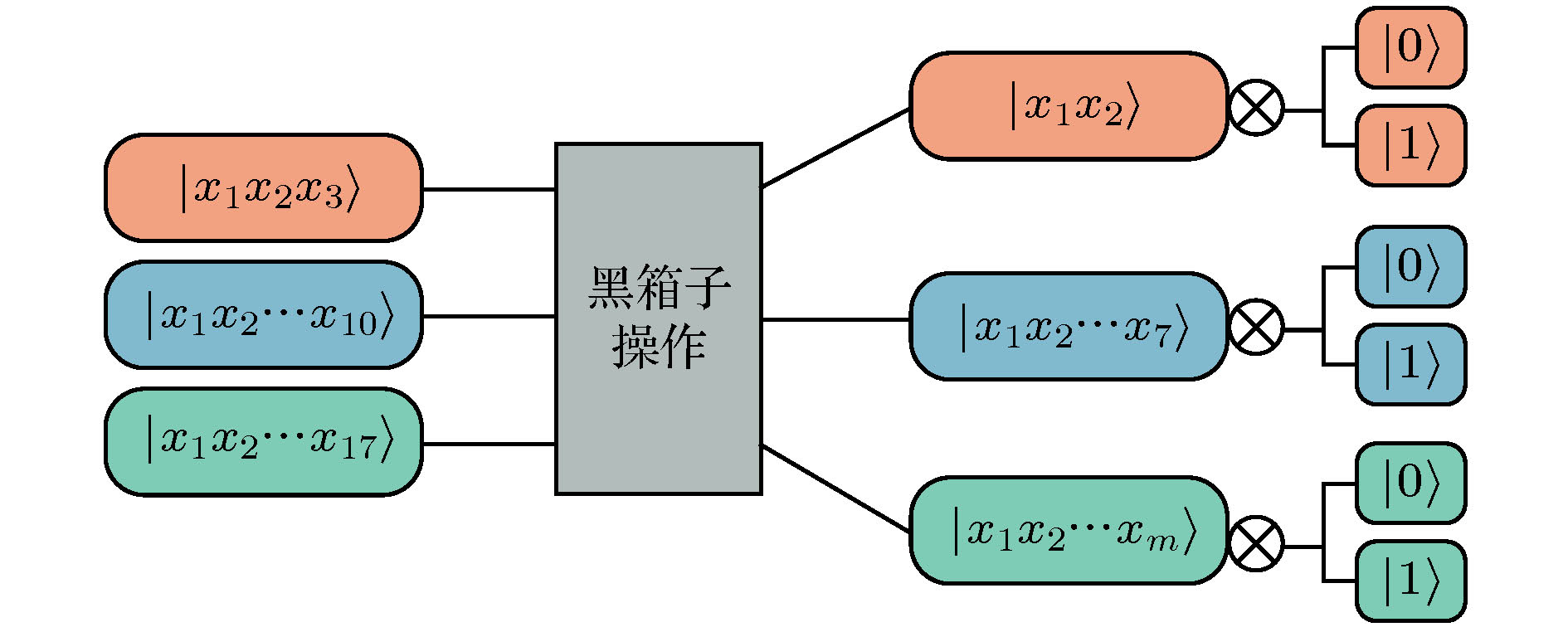
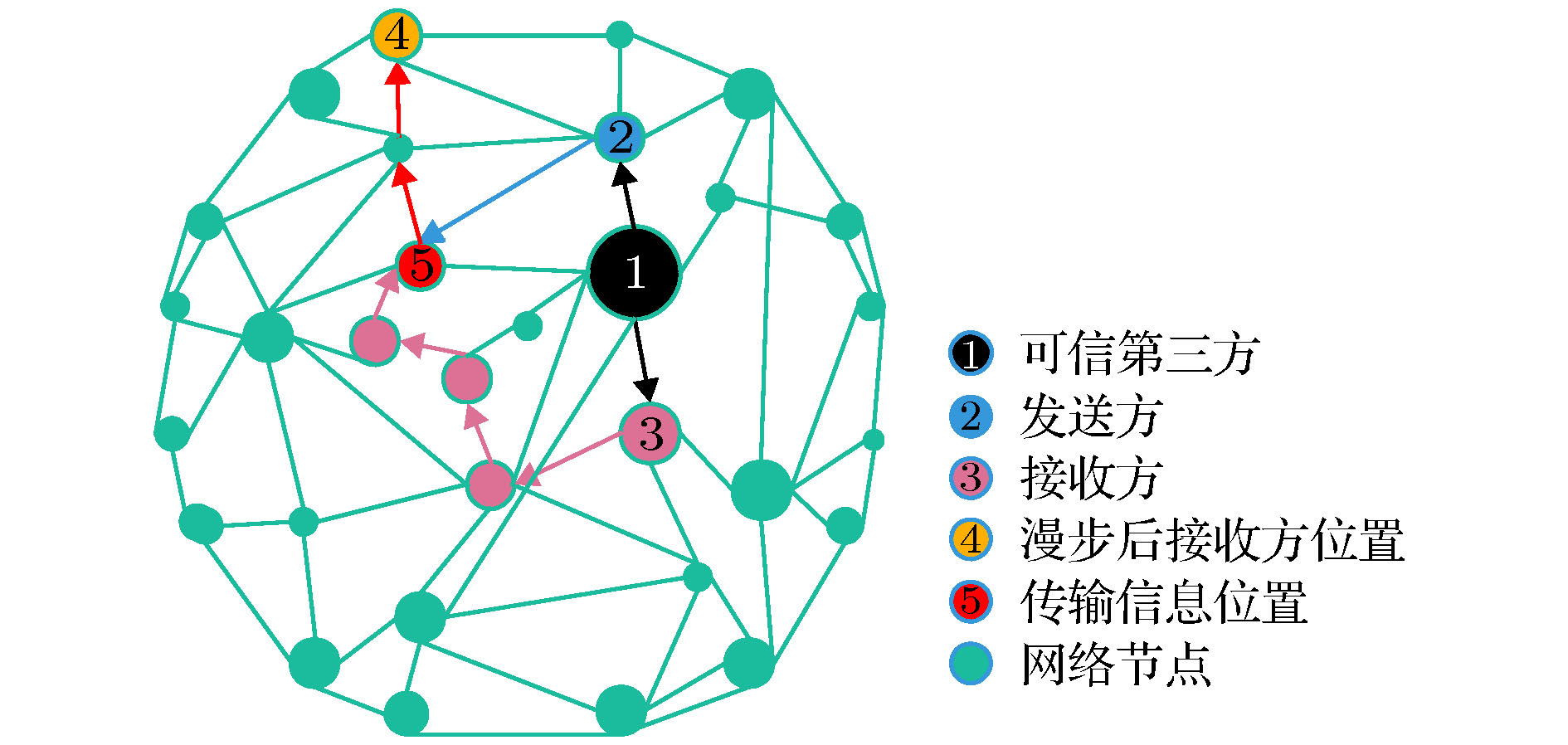
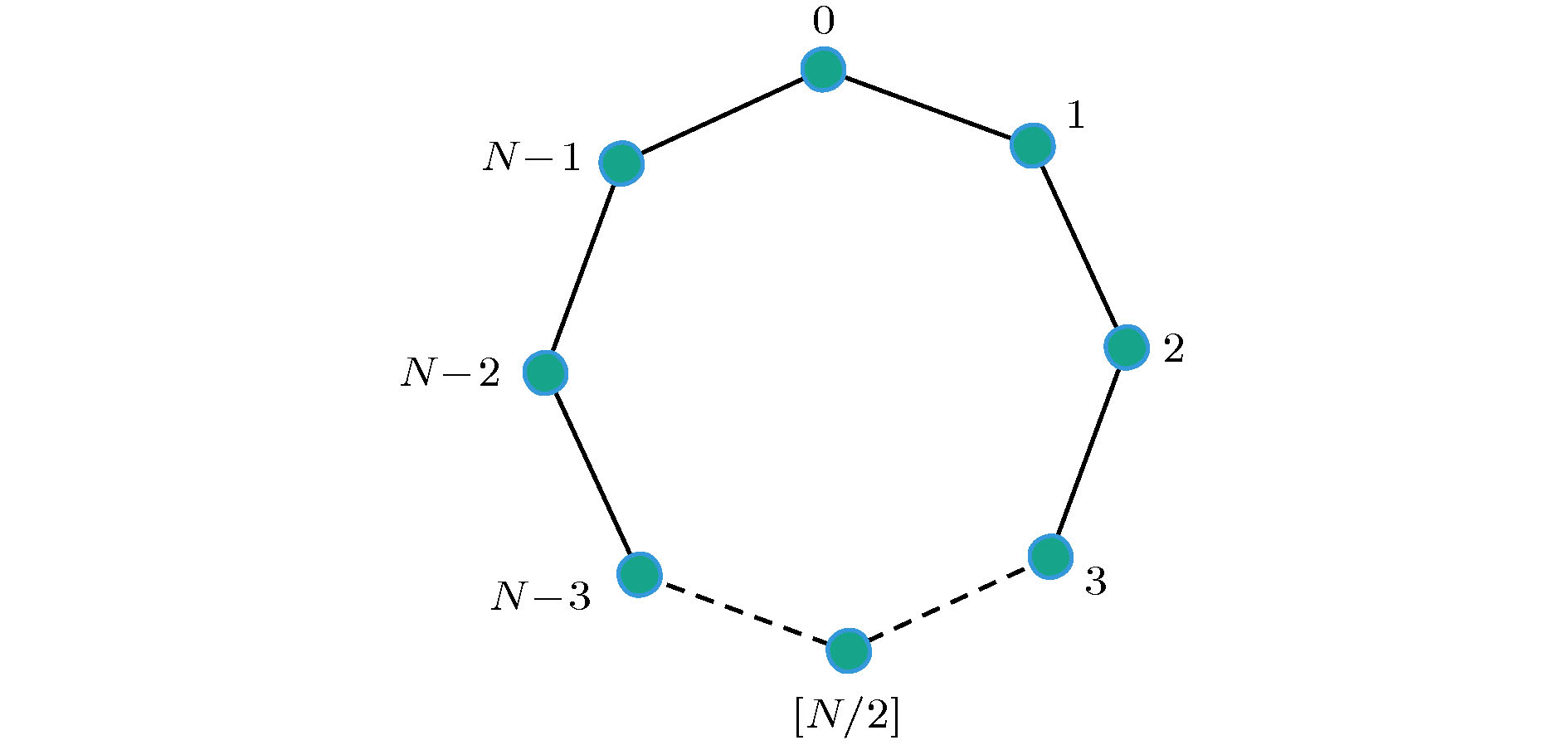
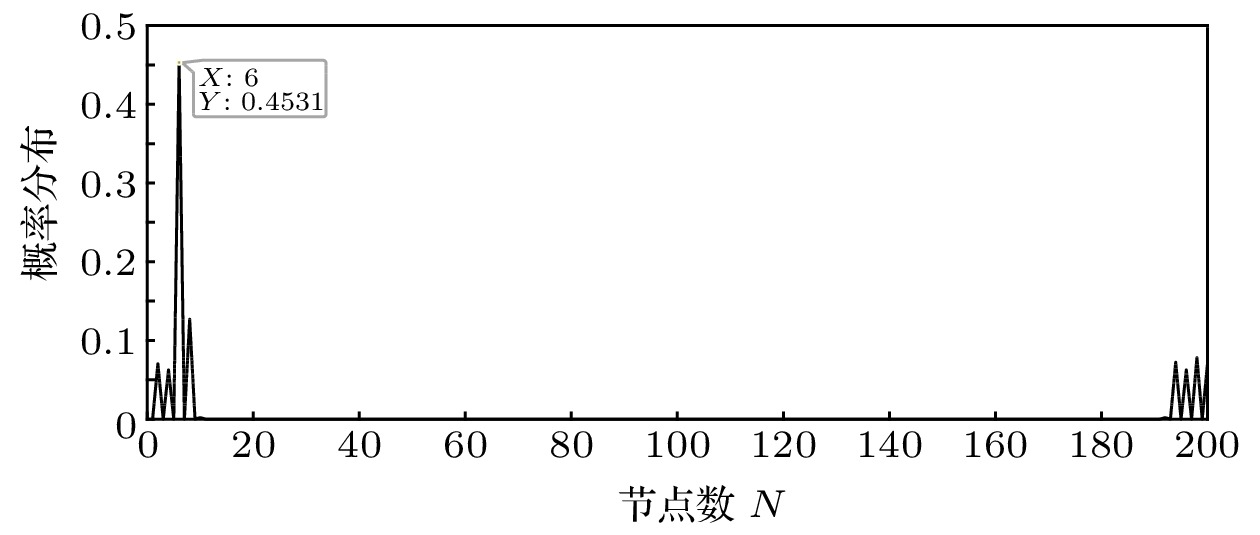
-
信息安全是信息化社会国家安全的基石与命脉, 而匿名量子通信是保护信息安全的重要通信方式之一. 利用量子漫步随机性有效解决身份信息泄露等敏感问题, 本文提出一种基于Cayley图上量子漫步的匿名通信方案. 首先, 通信双方隐藏自身身份信息, 发送方Alice通过逻辑或操作匿名选择接收方Bob. 其次, 可信第三方与通信双方利用BB84协议生成和分发安全密钥, Alice根据安全密钥对信息序列进行加密, 获得盲化信息; Bob利用联合Bell态测量和安全密钥进行签名, 可信第三方验证签名信息. 再次, 可信第三方依据傅里叶变换计算Bob量子漫步的位置概率分布函数, 将概率最大值对应的位置信息转换为确认帧发送给Alice; Alice利用量子降维压缩算法减少传输信息比特数, 并利用安全密钥完成信息加密后将信息传输至确认帧表示的位置, Bob利用量子漫步搜索位置节点获取传输信息, 完成匿名量子通信. 最后, 对方案进行安全分析, 并给出200个节点Cayley图的数值仿真结果, 漫步10步时, 第6个节点的概率最大为45.31%. 根据仿真结果, 本方案通信过程中Bob漫步10步时被窃听到具体位置的概率近似为6 × 10–7%.Information security is the cornerstone and lifeblood of national security in the information society, and anonymous quantum communication is one of the important ways to protect information security. Using quantum walk randomness to effectively solve sensitive problems such as leakage of identity information. In this paper, an anonymous communication scheme based on quantum walks on the Cayley graph is proposed. First, both parties in the communication hide their identity information, and the sender Alice anonymously selects the receiver Bob through logic or operation. Secondly, the trusted third party and the communicating parties use the BB84 protocol to generate and distribute the security key. Alice encrypts the information sequence according to the security key to obtain the blind information; Bob uses the joint Bell state measurement and security key to sign and the trusted third party verifies the signature information. Third, the trusted third party calculates the position probability distribution function of Bob’s quantum walk via the Fourier transform, converts the position information corresponding to the maximum probability into a confirmation frame and sends it to Alice; Alice uses the quantum compression algorithm by decreasing dimensions to reduce the number of transmitted information bits(the length of the information bit can be reduced by up to 37.5%) and uses the security key to complete the information encryption and then transmit the information to the location indicated by the confirmation frame. Bob uses quantum walks to search the location node to obtain the transmission information and complete the anonymous quantum communication. Finally, the security analysis of the scheme is carried out, and the numerical simulation results of the Cayley graph of 200 nodes are given. At the 10-step walk, the maximal probability of the 6th node is 45.31%. According to the simulation results, the probability that Bob is eavesdropped on the specific location at his 10-step walk during the communication of this scheme is approximately 6 × 10–7%, so the receiver can avoid the identity information from the eavesdropping with a high probability, and the quantum network anonymity protocol is not broken.
-
Keywords:
- anonymous quantum communication /
- quantum networks /
- quantum walk
[1] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[2] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1892
[3] 胡钰安, 叶志清 2014 光子学报 43 827001
Google Scholar
Hu Y A, Ye Z Q 2014 Acta Photon. Sin. 43 827001
Google Scholar
[4] Unnikrishnan A, MacFarlane I J, Yi R, Diamanti E, Markham D, Kerenidis I 2019 Phys. Rev. Lett. 122 240510
[5] Brassard G, Broadbent A, Fitzsimons J, Gambs S, Tapp A 2007 13 th International Conference on the Theory and Application of Cryptology and Information Security Kuching, Malaysia, December 2–6, 2007 pp460–473
[6] 陈鹏, 蔡有勋, 蔡晓菲, 施丽慧, 余旭涛 2015 64 040301
Chen P, Cai Y X, Cai X F, Shi L H, Yu X T 2015 Acta Phy. Sin. 64 040301
[7] 聂敏, 王林飞, 杨光, 张美玲, 裴昌幸 2015 64 210303
Google Scholar
Nie M, Wang L F, Yang G, Zhang M L, Pei C X 2015 Acta Phy. Sin. 64 210303
Google Scholar
[8] Wehner S 2004 Ph. D. Dissertation (Holland: Universiteit van Amsterdam)
[9] Chaum D 1988 J. Cryptol. 1 1
Google Scholar
[10] Chen X B, Sun Y R, Xu G 2019 Inf. Sci. 501 172
Google Scholar
[11] Xu G, Xiao K, Li Z P, Niu X X, Ryan M 2019 CMC-Comput. Mater. Con. 58 809
[12] Lipinska V, Murta G, Wehner S 2018 Phys. Rev. A 98 052320
Google Scholar
[13] 薛鹏, 郭光灿 2002 物理 31 385
Google Scholar
Xue P, Guo G C 2002 Physics 31 385
Google Scholar
[14] Boykin P O 2002 Ph. D. Dissertation (Los Angeles: University of California)
[15] Christandl M, Wehner S 2005 11th International Conference on the Theory and Application of Cryptology and Information Chennai, India, December 4–8, 2005 pp217–235
[16] Bouda J, Sprojcar J 2007 First International Conference on Quantum, Nano, and Micro Technologies Gosier, Guadeloupe, January 2–6, 2007 p12
[17] Jiang L, He G Q, Nie D, Xiong J, Zeng G H 2012 Phys. Rev. A 85 042309
Google Scholar
[18] 周南润, 龚黎华, 刘三秋, 曾贵华 2007 56 5066
Google Scholar
Zhou N R, Gong L H, Liu S Q, Zeng G H 2007 Acta Phys. Sin. 56 5066
Google Scholar
[19] Montanaro A 2016 NPJ Quantum Inf. 2 15023
Google Scholar
[20] 杨乐, 李凯, 戴宏毅, 张明 2019 68 140301
Google Scholar
Yang L, Li K, Dai H Y, Zhang M 2019 Acta Phys. Sin. 68 140301
Google Scholar
[21] Travaglione B C, Milburn G J 2002 Phys. Rev. A 65 032310
Google Scholar
[22] Childs A M, Goldstone J 2004 Phys. Rev. A 70 022314
Google Scholar
[23] Childs A M, Cleve R, Deotto E, Farhi E, Gutmann S, Spielman D A 2003 Proceedings of the Thirty-fifth Annual ACM Symposium on Theory of Computing San Diego, America, June 9–11, 2003 pp59–68
[24] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[25] Childs A M 2009 Phys. Rev. Lett. 102 180510
[26] Zhan H 2019 Quantum Inf. Process. 18 369
Google Scholar
[27] Costa P, de Melo F, Portugal R 2019 Phys. Rev. A 100 042320
Google Scholar
[28] Di Molfetta G, Arrighi P 2020 Quantum Inf. Process. 19 47
Google Scholar
[29] Wong T G 2019 Phys. Rev. A 100 062325
Google Scholar
[30] Szigeti B E, Homa G, Zimborás Z, Barankai N 2019 Phys. Rev. A 100 062320
Google Scholar
[31] Wang Y, Shang Y, Xue P 2017 Quantum Inf. Process. 16 221
Google Scholar
[32] Feng Y Y, Shi R H, Shi J J, Zhou J, Guo Y 2019 Quantum Inf. Process. 18 154
Google Scholar
[33] Li H J, Li J, Xiang N, Zheng Y, Yang Y G, Naseri M 2019 Quantum Inf. Process. 18 316
Google Scholar
[34] Abd-El-Atty B, El-Latif A A A, Venegas-Andraca S E 2019 Quantum Inf. Process. 18 272
Google Scholar
[35] Xu P A, He Z X, Qiu T H, Ma H Y 2020 Opt. Express 28 12508
Google Scholar
[36] Shi P, Li N C, Wang S M, Liu Z, Ren M R, Ma H Y 2019 Sensors 19 5257
Google Scholar
[37] Ma H Y, Teng J K, Hu T, Shi P, Wang S M 2020 Wireless. Pers. Commun. https://doi.org/10.1088/1674-1056/ab773 e [quant-ph]
[38] Zhao J B, Zhang W B, Ma Y L, Zhang X H, Ma H Y 2020 Appl. Sci. 10 1935
Google Scholar
[39] Ye C Q, Ye T Y 2019 Int. J. Theor. Phys. 58 1282
Google Scholar
[40] Qin L G, Wang Z Y, Wu S C, Gong S Q, Ma H Y, Jing J 2018 Opt. Commun. 410 102
Google Scholar
[41] Gong L, Qiu K, Deng C, Zhou N 2019 Opt. Laser Technol. 115 257
Google Scholar
[42] Chen X B, Wang Y L, Xu G, Yang Y Y 2019 IEEE Access 7 13634
Google Scholar
[43] Li H J, Chen X B, Wang Y L, Hou Y Y, Li J 2019 Quantum Inf. Process. 18 16
Google Scholar
[44] Facer C, Twamley J, Cresser J 2008 Phys. Rev. A 77 012334
Google Scholar
[45] Deng F G, Long G L 2004 Phys. Rev. A 69 052319
Google Scholar
[46] 龙桂鲁, 王川, 李岩松, 邓富国 2011 中国科学: 物理学 力学 天文学 41 332
Long G L, Wang C, Li Y S, Deng F G 2011 Sci. Sin. Phys. Mech. Astron. 41 332
[47] Kempf A, Portugal R 2009 Phys. Rev. A 79 052317
Google Scholar
[48] Childs A M 2010 Commun. Math. Phys. 294 281
[49] 刘欣, 梁燕霞, 聂敏, 魏媛媛 2017 光电子·激光 11 7
Liu X, Liang Y X, Nie M, Wei Y Y 2017 J. Optoelectron. Laser 11 7
[50] 马鸿洋, 张鑫, 徐鹏翱, 刘芬, 范兴奎 2020 通信学报 41 190
Google Scholar
Ma H Y, Zhang X, Xu P A, Liu F, Fan X K 2020 J. Commun. 41 190
Google Scholar
[51] Diaconis P, Rockmore D 1990 J. Am. Math. Soc. 3 297
Google Scholar
[52] Hsiao H C, Kim T J, Perring A, Yamada A 2012 IEEE Secur. Privacy 19 506
-
图 5 量子漫步10步时概率分布图
Fig. 5. Probability distribution diagram for quantum walk in 10 steps.
表 1 信息N和签名Sor的对应关系
Table 1. Correspondence between information N and Sor signature
Alice信息序列$ N_{j} $ Bob签名序列$ Sor_{j} $ 00 00 或 01 01 10 或 11 10 00 或 11 11 01 或 11 
下载: 导出CSV
表 2 数值仿真结果
Table 2. Numerical simulation results
时间 节点总数 位置 概率/% 3 100 2 72.72 10 500 6 45.31 30 200 或 500 20 25.92 50 200 或 500 34 18.95 100 100 68 12.20 200 200 138 10.81
下载: 导出CSV
-
[1] Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706
Google Scholar
[2] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1892
[3] 胡钰安, 叶志清 2014 光子学报 43 827001
Google Scholar
Hu Y A, Ye Z Q 2014 Acta Photon. Sin. 43 827001
Google Scholar
[4] Unnikrishnan A, MacFarlane I J, Yi R, Diamanti E, Markham D, Kerenidis I 2019 Phys. Rev. Lett. 122 240510
[5] Brassard G, Broadbent A, Fitzsimons J, Gambs S, Tapp A 2007 13 th International Conference on the Theory and Application of Cryptology and Information Security Kuching, Malaysia, December 2–6, 2007 pp460–473
[6] 陈鹏, 蔡有勋, 蔡晓菲, 施丽慧, 余旭涛 2015 64 040301
Chen P, Cai Y X, Cai X F, Shi L H, Yu X T 2015 Acta Phy. Sin. 64 040301
[7] 聂敏, 王林飞, 杨光, 张美玲, 裴昌幸 2015 64 210303
Google Scholar
Nie M, Wang L F, Yang G, Zhang M L, Pei C X 2015 Acta Phy. Sin. 64 210303
Google Scholar
[8] Wehner S 2004 Ph. D. Dissertation (Holland: Universiteit van Amsterdam)
[9] Chaum D 1988 J. Cryptol. 1 1
Google Scholar
[10] Chen X B, Sun Y R, Xu G 2019 Inf. Sci. 501 172
Google Scholar
[11] Xu G, Xiao K, Li Z P, Niu X X, Ryan M 2019 CMC-Comput. Mater. Con. 58 809
[12] Lipinska V, Murta G, Wehner S 2018 Phys. Rev. A 98 052320
Google Scholar
[13] 薛鹏, 郭光灿 2002 物理 31 385
Google Scholar
Xue P, Guo G C 2002 Physics 31 385
Google Scholar
[14] Boykin P O 2002 Ph. D. Dissertation (Los Angeles: University of California)
[15] Christandl M, Wehner S 2005 11th International Conference on the Theory and Application of Cryptology and Information Chennai, India, December 4–8, 2005 pp217–235
[16] Bouda J, Sprojcar J 2007 First International Conference on Quantum, Nano, and Micro Technologies Gosier, Guadeloupe, January 2–6, 2007 p12
[17] Jiang L, He G Q, Nie D, Xiong J, Zeng G H 2012 Phys. Rev. A 85 042309
Google Scholar
[18] 周南润, 龚黎华, 刘三秋, 曾贵华 2007 56 5066
Google Scholar
Zhou N R, Gong L H, Liu S Q, Zeng G H 2007 Acta Phys. Sin. 56 5066
Google Scholar
[19] Montanaro A 2016 NPJ Quantum Inf. 2 15023
Google Scholar
[20] 杨乐, 李凯, 戴宏毅, 张明 2019 68 140301
Google Scholar
Yang L, Li K, Dai H Y, Zhang M 2019 Acta Phys. Sin. 68 140301
Google Scholar
[21] Travaglione B C, Milburn G J 2002 Phys. Rev. A 65 032310
Google Scholar
[22] Childs A M, Goldstone J 2004 Phys. Rev. A 70 022314
Google Scholar
[23] Childs A M, Cleve R, Deotto E, Farhi E, Gutmann S, Spielman D A 2003 Proceedings of the Thirty-fifth Annual ACM Symposium on Theory of Computing San Diego, America, June 9–11, 2003 pp59–68
[24] Sansoni L, Sciarrino F, Vallone G, Mataloni P, Crespi A, Ramponi R, Osellame R 2012 Phys. Rev. Lett. 108 010502
Google Scholar
[25] Childs A M 2009 Phys. Rev. Lett. 102 180510
[26] Zhan H 2019 Quantum Inf. Process. 18 369
Google Scholar
[27] Costa P, de Melo F, Portugal R 2019 Phys. Rev. A 100 042320
Google Scholar
[28] Di Molfetta G, Arrighi P 2020 Quantum Inf. Process. 19 47
Google Scholar
[29] Wong T G 2019 Phys. Rev. A 100 062325
Google Scholar
[30] Szigeti B E, Homa G, Zimborás Z, Barankai N 2019 Phys. Rev. A 100 062320
Google Scholar
[31] Wang Y, Shang Y, Xue P 2017 Quantum Inf. Process. 16 221
Google Scholar
[32] Feng Y Y, Shi R H, Shi J J, Zhou J, Guo Y 2019 Quantum Inf. Process. 18 154
Google Scholar
[33] Li H J, Li J, Xiang N, Zheng Y, Yang Y G, Naseri M 2019 Quantum Inf. Process. 18 316
Google Scholar
[34] Abd-El-Atty B, El-Latif A A A, Venegas-Andraca S E 2019 Quantum Inf. Process. 18 272
Google Scholar
[35] Xu P A, He Z X, Qiu T H, Ma H Y 2020 Opt. Express 28 12508
Google Scholar
[36] Shi P, Li N C, Wang S M, Liu Z, Ren M R, Ma H Y 2019 Sensors 19 5257
Google Scholar
[37] Ma H Y, Teng J K, Hu T, Shi P, Wang S M 2020 Wireless. Pers. Commun. https://doi.org/10.1088/1674-1056/ab773 e [quant-ph]
[38] Zhao J B, Zhang W B, Ma Y L, Zhang X H, Ma H Y 2020 Appl. Sci. 10 1935
Google Scholar
[39] Ye C Q, Ye T Y 2019 Int. J. Theor. Phys. 58 1282
Google Scholar
[40] Qin L G, Wang Z Y, Wu S C, Gong S Q, Ma H Y, Jing J 2018 Opt. Commun. 410 102
Google Scholar
[41] Gong L, Qiu K, Deng C, Zhou N 2019 Opt. Laser Technol. 115 257
Google Scholar
[42] Chen X B, Wang Y L, Xu G, Yang Y Y 2019 IEEE Access 7 13634
Google Scholar
[43] Li H J, Chen X B, Wang Y L, Hou Y Y, Li J 2019 Quantum Inf. Process. 18 16
Google Scholar
[44] Facer C, Twamley J, Cresser J 2008 Phys. Rev. A 77 012334
Google Scholar
[45] Deng F G, Long G L 2004 Phys. Rev. A 69 052319
Google Scholar
[46] 龙桂鲁, 王川, 李岩松, 邓富国 2011 中国科学: 物理学 力学 天文学 41 332
Long G L, Wang C, Li Y S, Deng F G 2011 Sci. Sin. Phys. Mech. Astron. 41 332
[47] Kempf A, Portugal R 2009 Phys. Rev. A 79 052317
Google Scholar
[48] Childs A M 2010 Commun. Math. Phys. 294 281
[49] 刘欣, 梁燕霞, 聂敏, 魏媛媛 2017 光电子·激光 11 7
Liu X, Liang Y X, Nie M, Wei Y Y 2017 J. Optoelectron. Laser 11 7
[50] 马鸿洋, 张鑫, 徐鹏翱, 刘芬, 范兴奎 2020 通信学报 41 190
Google Scholar
Ma H Y, Zhang X, Xu P A, Liu F, Fan X K 2020 J. Commun. 41 190
Google Scholar
[51] Diaconis P, Rockmore D 1990 J. Am. Math. Soc. 3 297
Google Scholar
[52] Hsiao H C, Kim T J, Perring A, Yamada A 2012 IEEE Secur. Privacy 19 506
下载:
计量
- 文章访问数: 6813
- PDF下载量: 103
- 被引次数: 0
