Boussinesq方程的Lax对、Bäcklund变换、对称群变换和Riccati展开相容性

刘萍; 徐恒睿; 杨建荣

doi:10.7498/aps.69.20191316

摘要

Boussinesq方程是流体力学等领域一个非常重要的方程. 本文推导了Boussinesq方程的Lax对. 借助于截断Painlevé展开, 得到了Boussinesq方程的自Bäcklund变换, 以及Boussinesq方程和Schwarzian形式的Boussinesq方程之间的Bäcklund变换. 探讨了Boussinesq方程的非局域对称, 研究了Boussinesq方程的单参数群变换和单参数子群不变解. 运用Riccati展开法研究了Boussinesq方程, 证明Boussinesq方程具有Riccati展开相容性, 得到了Boussinesq方程的孤立波-椭圆余弦波解.

关键词:

Abstract

The Boussinesq equation is a very important equation in fluid mechanics and some other disciplines. A Lax pair of the Boussinesq equation is proposed. With the help of the truncated Painlevé expansion, auto-Bäcklund transformation of the Boussinesq equation and Bäcklund transformation between the Boussinesq equation and the Schwarzian Boussinesq equation are demonstrated. Nonlocal symmetries of the Boussinesq equation are discussed. One-parameter subgroup invariant solutions and one-parameter group transformations are obtained. The consistent Riccati expansion solvability of the Boussinesq equation is proved and some interaction structures between soliton-cnoidal waves are obtained by consistent Riccati expansion.

Keywords:

作者及机构信息

1.
电子科技大学中山学院电子信息学院, 中山　528402

2.
电子科技大学物理学院, 成都　610054

3.
上饶师范学院物理与电子信息学院, 上饶　334001

通信作者: 刘萍, liuping49@126.com

基金项目: 国家自然科学基金(批准号: 11775047、11865013)和中山市科技计划项目(批准号: 2017B1016)资助的课题

Authors and contacts

1.
School of Electronic and Information Engineering, University of Electronic Science and Technology of China, Zhongshan Institute, Zhongshan 528402, China

2.
School of Physics, University of Electronic Science and Technology of China, Chengdu 610054, China

3.
School of Physics and Electronic Information, Shangrao Normal University, Shangrao 334001, China

Corresponding author: Liu Ping, liuping49@126.com

文章全文 : translate this paragraph

参考文献

[1]	Boussinesq J 1872 J. Math. Pures Appl. 17 55
[2]	Ursell F 1953 Proc. Cambridge Philos. Soc. 49 685 Google Scholar
[3]	Daripa P 1998 J. Comput. Appl. Math. 100 161 Google Scholar
[4]	Guo B, Gao Z, Lin J 2016 Commun. Theor. Phys. 64 589
[5]	Liu W 2009 Z. Naturforschung A 64 709 Google Scholar
[6]	Benny D J, Luke J C 1964 J. Math. Phys. 43 309 Google Scholar
[7]	Himonas A A, Mantzavinos D 2015 J. Differ. Equations 258 3107 Google Scholar
[8]	Li S, Zhang W, Bu X 2017 J. Math. Anal. Appl. 449 96 Google Scholar
[9]	Weiss J 1983 J. Math. Phys. 24 1405 Google Scholar
[10]	Guo B X, Lin J 2013 Int. J. Mod. Phys. B 30 1640013
[11]	Guo B X, Gao Z J, Lin J 2016 Commun. Theor. Phys. 66 589 Google Scholar
[12]	Liu Y K, Li B 2016 Chin. J. Phys. 54 718 Google Scholar
[13]	Gao X N, Lou SY, Tang X Y 2013 J. High Energy Phys. 5 029
[14]	Olver P J 1993 Applications of Lie Group to Differential Equations (2nd ed.) (New York: Springer) pp75–238
[15]	Liu P, Zeng B Q, Ren B 2015 Commun. Theor. Phys. 63 413 Google Scholar
[16]	Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202 Google Scholar
[17]	Liu P, Zeng B Q, Deng B B, Yang J R 2015 AIP Adv. 5 087162 Google Scholar
[18]	Liu P, Wang Y X, Ren B, Li J H 2016 Commun. Theor. Phys. 66 595 Google Scholar
[19]	焦小玉, 贾曼, 安红利 2019 68 140201 Google Scholar Jiao X Y, Jia M, An H L 2019 Acta Phys. Sin. 68 140201 Google Scholar
[20]	Lou S Y 2015 Stud. Appl. Math. 134 372 Google Scholar

施引文献

图 1 满足(47)式的碰撞波解(49)式. 自由参数为{n = 0.2, m = 0.5, a₁ = 1, a₃ = 1, k₁ = 1, k₂ = 1, ω₂ = 1, α = –0.8, β = 1}

Fig. 1. The solution (49) with Formula (47). The free parameters are {n = 0.2, m = 0.5, a₁ = 1, a₃ = 1, k₁ = 1, k₂ = 1, ω₂ = 1, α = –0.8, β = 1}.

下载: 全尺寸图片幻灯片

图 2 满足(47)式的碰撞波解(49)式. 自由参数为 {n = 0.2, m = 0.9, a₁ = 1, a₃ = 1, k₁ = 1, k₂ = 1, ω₂ = 1, α = –0.8, β = 1}

Fig. 2. The solution (49) with Formula (47). The free parameters are {n = 0.2, m = 0.9, a₁ = 1, a₃ = 1, k₁ = 1, k₂ = 1, ω₂ = 1, α = –0.8, β = 1}.

下载: 全尺寸图片幻灯片

图 3 u的密度函数图. 图(a)的参数与图1相同, 图(b)的参数与图2相同

Fig. 3. The density of u. The parameters of the Fig. (a) are the same as those of Figure 1 and the parameters of the Fig. (b) are the same as those of Figure 2.

下载: 全尺寸图片幻灯片

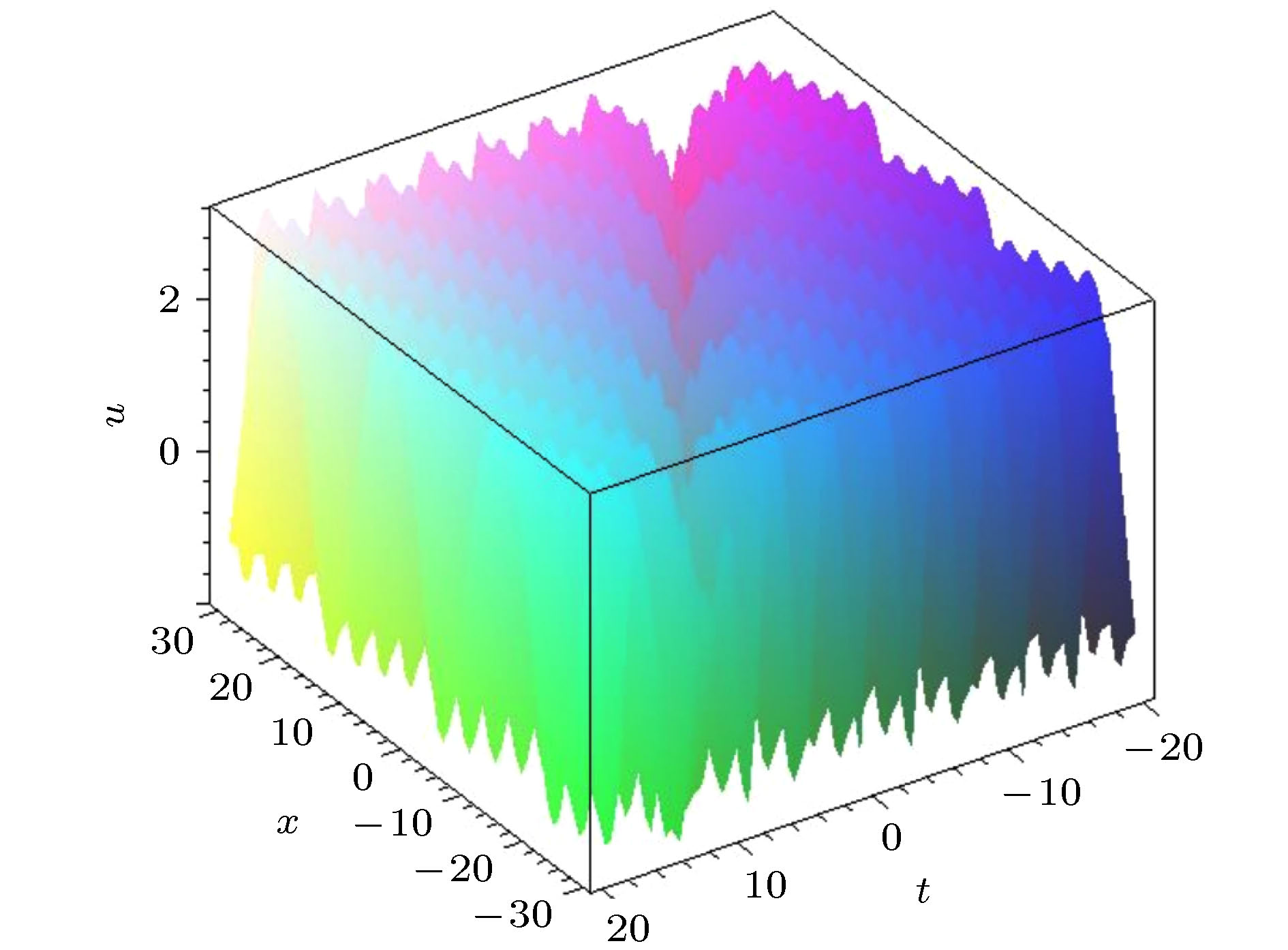
图 4 参数关系满足(48)式的碰撞波解(49)式的演化图. 自由参数为 {n = 0.4, a₁ = 1, a₂ = 1, a₃ = 2.2, k₁ = 1, k₂ = –0.22, ω₂ = 1, α = –400, β = 80}

Fig. 4. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are chosen as {n = 0.4, a₁ = 1, a₂ = 1, a₃ = 2.2, k₁ = 1, k₂ = –0.22, ω₂ = 1, α = –400, β = 80}.

下载: 全尺寸图片幻灯片

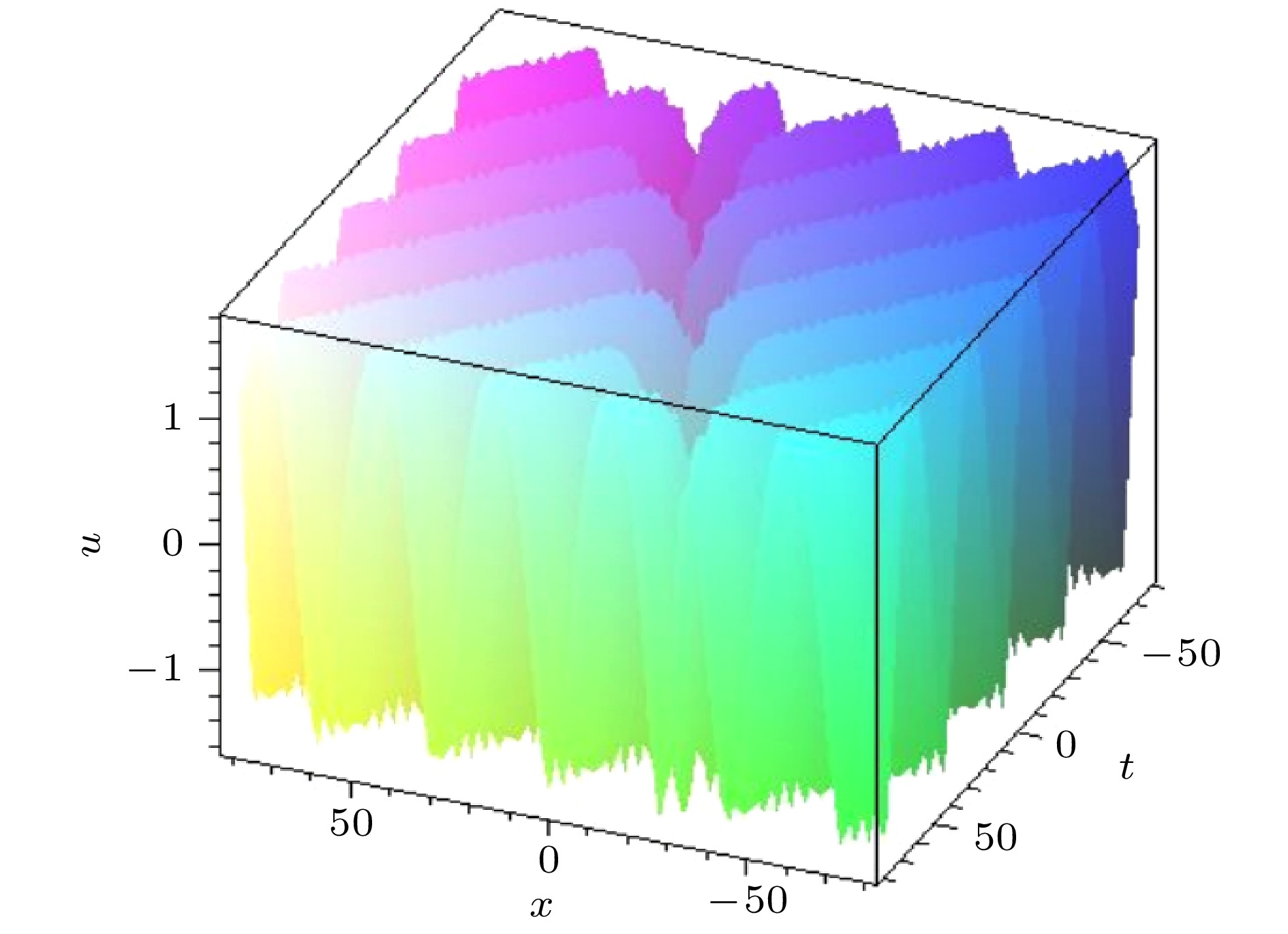
图 5 参数关系满足(48)式的碰撞波解(49)式. 自由参数为{n = 0.6, a₁ = 2, a₂ = 1, a₃ = 4, k₁ = 1, k₂ = –0.12, ω₂ = 0.1, α = –14, β = 6}

Fig. 5. The interaction solution (49) with parameter satisfying Formula (48). The free parameters are selected as {n = 0.6, a₁ = 2, a₂ = 1, a₃ = 4, k₁ = 1, k₂ = –0.12, ω₂ = 0.1, α = –14, β = 6}.

下载: 全尺寸图片幻灯片

图 6 u的密度函数图. 图(a)对应图4, 图(b)对应图5

Fig. 6. The density of u. The Fig. (a) is related to Fig. 4 and the Fig. (b) is corresponding to Fig. 5.

下载: 全尺寸图片幻灯片

map

[1]	Boussinesq J 1872 J. Math. Pures Appl. 17 55
[2]	Ursell F 1953 Proc. Cambridge Philos. Soc. 49 685 Google Scholar
[3]	Daripa P 1998 J. Comput. Appl. Math. 100 161 Google Scholar
[4]	Guo B, Gao Z, Lin J 2016 Commun. Theor. Phys. 64 589
[5]	Liu W 2009 Z. Naturforschung A 64 709 Google Scholar
[6]	Benny D J, Luke J C 1964 J. Math. Phys. 43 309 Google Scholar
[7]	Himonas A A, Mantzavinos D 2015 J. Differ. Equations 258 3107 Google Scholar
[8]	Li S, Zhang W, Bu X 2017 J. Math. Anal. Appl. 449 96 Google Scholar
[9]	Weiss J 1983 J. Math. Phys. 24 1405 Google Scholar
[10]	Guo B X, Lin J 2013 Int. J. Mod. Phys. B 30 1640013
[11]	Guo B X, Gao Z J, Lin J 2016 Commun. Theor. Phys. 66 589 Google Scholar
[12]	Liu Y K, Li B 2016 Chin. J. Phys. 54 718 Google Scholar
[13]	Gao X N, Lou SY, Tang X Y 2013 J. High Energy Phys. 5 029
[14]	Olver P J 1993 Applications of Lie Group to Differential Equations (2nd ed.) (New York: Springer) pp75–238
[15]	Liu P, Zeng B Q, Ren B 2015 Commun. Theor. Phys. 63 413 Google Scholar
[16]	Liu Y K, Li B 2017 Chin. Phys. Lett. 34 010202 Google Scholar
[17]	Liu P, Zeng B Q, Deng B B, Yang J R 2015 AIP Adv. 5 087162 Google Scholar
[18]	Liu P, Wang Y X, Ren B, Li J H 2016 Commun. Theor. Phys. 66 595 Google Scholar
[19]	焦小玉, 贾曼, 安红利 2019 68 140201 Google Scholar Jiao X Y, Jia M, An H L 2019 Acta Phys. Sin. 68 140201 Google Scholar
[20]	Lou S Y 2015 Stud. Appl. Math. 134 372 Google Scholar

[1]	公睿智, 王灯山. 散焦型非线性薛定谔方程的Whitham调制理论及其间断初值问题解的分类和演化. , 2023, 72(10): 100503. doi: 10.7498/aps.72.20230172
[2]	于兴江, 刘希强. 时间分数阶Boussinesq方程的李对称分析. , 2013, 62(23): 230201. doi: 10.7498/aps.62.230201
[3]	曹小群, 宋君强, 张卫民, 朱小谦, 赵军. Boussinesq方程组的广义变分原理. , 2011, 60(8): 080401. doi: 10.7498/aps.60.080401
[4]	套格图桑, 斯仁道尔吉. 广义Boussinesq方程的无穷序列新精确解. , 2010, 59(7): 4413-4419. doi: 10.7498/aps.59.4413
[5]	王静. 一个新的广义的Riccati方程有理展开法及其应用. , 2010, 59(5): 2924-2931. doi: 10.7498/aps.59.2924
[6]	套格图桑, 斯仁道尔吉. 用Riccati方程构造非线性差分微分方程新的精确解. , 2009, 58(9): 5894-5902. doi: 10.7498/aps.58.5894
[7]	莫嘉琪, 程燕. 广义Boussinesq方程的同伦映射近似解. , 2009, 58(7): 4379-4382. doi: 10.7498/aps.58.4379
[8]	杨先林, 唐驾时. 利用耦合的Riccati方程组构造微分-差分方程精确解. , 2008, 57(6): 3305-3311. doi: 10.7498/aps.57.3305
[9]	吴勇旗. (2+1)维Boussinesq方程的新的周期解. , 2008, 57(9): 5390-5394. doi: 10.7498/aps.57.5390
[10]	单梁, 梁彦, 李军, 王执铨. 统一混沌系统的状态Riccati方程同步法. , 2007, 56(8): 4366-4371. doi: 10.7498/aps.56.4366
[11]	贺锋, 郭启波, 刘辽. 用三角函数法获得非线性Boussinesq方程的广义孤子解. , 2007, 56(8): 4326-4330. doi: 10.7498/aps.56.4326
[12]	高亮, 徐伟, 唐亚宁, 申建伟. 一类广义Boussinesq方程和Boussinesq-Burgers方程新的显式精确解. , 2007, 56(4): 1860-1869. doi: 10.7498/aps.56.1860
[13]	雍雪林, 张鸿庆. 推广的投影Riccati方程法及其应用. , 2005, 54(6): 2514-2519. doi: 10.7498/aps.54.2514
[14]	曾昕, 张鸿庆. (2+1)维Boussinesq方程的Backlund变换与精确解. , 2005, 54(4): 1476-1480. doi: 10.7498/aps.54.1476
[15]	李齐良, 朱海东, 唐向宏, 李承家, 王小军, 林理彬. 多波长系统孤子耦合方程的可积性. , 2004, 53(6): 1623-1628. doi: 10.7498/aps.53.1623
[16]	周振江, 李志斌. Broer-Kaup系统的达布变换和新的精确解. , 2003, 52(2): 262-266. doi: 10.7498/aps.52.262
[17]	佘守宪. 用Riccati变换求解同调谐振子. , 2002, 51(5): 1054-1056. doi: 10.7498/aps.51.1054
[18]	闫振亚, 张鸿庆. 新的Lax可积发展方程族及其无限维双-哈密顿结构. , 2001, 50(7): 1232-1236. doi: 10.7498/aps.50.1232
[19]	王宁. Gelfand-Dickey算子分解,B?cklund-Darboux变换及对称. , 1999, 48(8): 1394-1398. doi: 10.7498/aps.48.1394
[20]	管习文, 仝殿民, 周焕强. XYZ自旋开链的Lax对及其边界K矩阵. , 1997, 46(4): 796-801. doi: 10.7498/aps.46.796

计量

文章访问数: 9622
PDF下载量: 252
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

Boussinesq方程的Lax对、Bäcklund变换、对称群变换和Riccati展开相容性