石墨烯莫尔超晶格体系的拓扑性质及光学研究进展

吕新宇; 李志强

doi:10.7498/aps.68.20191317

摘要

当两个晶格常数或晶格转角不同的二维材料叠加在一起时会出现周期性的莫尔条纹结构, 这种莫尔超晶格形成了一个新的二维周期势, 可以大大改变原有体系的物理性质. 最近石墨烯与石墨烯、石墨烯与六方氮化硼形成的莫尔超晶格提供了一个非常有趣的体系, 在该体系中石墨烯的电子能带结构发生了根本性的改变, 在原本的能谷处产生了额外的超晶格小能带, 由此产生了十分丰富的强关联效应和拓扑效应. 本文介绍关于石墨烯莫尔超晶格体系拓扑性质的理论和实验研究进展, 主要包括双层石墨烯的畴壁拓扑态、转角双层石墨烯的小能带拓扑态、ABC堆叠三层石墨烯以及转角双层堆叠双层石墨烯的拓扑性质等, 最后介绍利用近场光学技术研究石墨烯莫尔超晶格体系的能带结构和新奇拓扑性质.

关键词:

Abstract

When 2D materials with different lattice constants or lattice rotation angles are stacked together, a periodic moiré pattern will appear. Such moiré superlattice introduces a new two dimensional periodic potential, which can greatly change the physical properties of the original systems. Recent experimental studies of moiré superlattices formed by graphene on graphene and graphene on hexagonal boron nitride have revealed very rich strong correlation effects and topological effects due to novel states in superlattice minibands. It has been shown that flat bands in graphene-based moiré superlattice systems can host both topological states and strongly correlated states, which can be controlled by an external electric field. In bilayer graphene, ABC stacked trilayer graphene and twisted bilayer-bilayer graphene, the number of valence and conduction bands near the Dirac point and even the band topology and bandwidth can be changed by varying the stacking angle between graphene layers or the applied bias voltage. Moreover, the competition between kinetic energy and coulomb interaction depends on the bandwidth and the external electric field, and at the so-called magic angle mott insulator states and superconductivity were observed. Twisted bilayer-bilayer graphene has also been predicted to show similar intriguing properties, including electrically tunable strongly correlated insulators, superconductivity and many rich topological states. In graphene-based moiré systems, the combination of topological states and strong correlations is expected to lead to a broad range of novel phenomena that are not achievable in other material systems. Therefore, graphene moiré systems is likely to bring substantial progress to the study of topological materials. In this paper, we review theoretical and experimental investigations of the topological properties of graphene moiré superlattices, including topological domain wall states in bilayer graphene and topological effects in twisted bilayer graphene, ABC trilayer graphene and twisted double bilayer graphene. The origins of topological properties of these systems are discussed as well as topological phenomena observed in various experiments. Finally, recent near-field optical studies of the band structure and novel topological properties of graphene moiré superlattices are discussed.

Keywords:

作者及机构信息

四川大学物理学院, 成都　610065

通信作者: 李志强, zhiqiangli@scu.edu.cn

基金项目: 国家自然科学基金(批准号: 11874271)资助的课题

Authors and contacts

College of Physics, Sichuan University, Chengdu 610065, China

Corresponding author: Li Zhi-Qiang, zhiqiangli@scu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11874271)

文章全文 : translate this paragraph

参考文献

[1]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[2]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[3]	Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405 Google Scholar
[4]	Wang Z J, Sun Y, Chen X Q, Franchini C, Xu G, Weng H M, Dai X, Fang Z 2012 Phys. Rev. B 85 195320 Google Scholar
[5]	Wang Z J, Weng H M, Wu Q S, Dai X, Fang Z 2013 Phys. Rev. B 88 125427 Google Scholar
[6]	Weng H M, Fang C, Fang Z, Bernrviget B A, Dai X 2015 Phys. Rev. X 5 011029
[7]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[8]	Zhang Y H, Mao D, Senthil T 2019 arXiv preprint arXiv: 1901 08209
[9]	Bultinck N, Chatterjee S, Zaletel M P 2019 arXiv preprint arXiv: 1901 08110
[10]	Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, P Jarillo-Herrero, Ashoori R C 2018 Nature 556 80 Google Scholar
[11]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[12]	Zhang Y H, Senthil T 2019 Phys. Rev. B 99 205150 Google Scholar
[13]	Chen G, Jiang L, Wu S, Lyu B, Li H, Chittari B L, Kenji W, Takashi T, Shi Z, Jeil J, Zhang Y, Wang F 2019 Nat. Phys. 15 237 Google Scholar
[14]	Chen G, Sharpe A L, Fox E J, Zhang Y H, Wang S, Jiang L, Lyu B, Watanabe K, Takashi T, Senthil T, David G G, Shi Z, Wang F 2019 arXiv preprint arXiv: 1905 06535
[15]	Chittari B L, Chen G, Zhang Y, Wang F, Jung J 2019 Phys. Rev. Lett. 122 016401 Google Scholar
[16]	Liu X, Hao Z, Khalaf E, Lee J Y, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2019 arXiv preprint arXiv: 1903 08130
[17]	Cao Y, Rodan-Legrain D, Rubies-Bigordà O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2019 arXiv preprint arXiv: 1903.08596
[18]	Shen C, Li N, Wang S, Zhao Y, Tang J, Liu J, Tian J, Chu Y, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D, Zhang G 2019 arXiv preprint arXiv: 1903 06952
[19]	Koshino M 2019 Phys. Rev. B 99 235406 Google Scholar
[20]	Chen Z G, Shi Z, Yang W, Lu X, Lai Y, Yan H, Yan H, Zhang G, Li Z 2014 Nat. Commun. 5 4461 Google Scholar
[21]	Wu S, Wang L, Lai Y, Shan W Y, Aivazian G, Zhang X, Taniguchi T, Watanabe K J, Xiao D, Dean C, Hone J, Li Z, Xu X 2016 Sci. Adv. 2 e1600002 Google Scholar
[22]	Jiang L, Shi Z, Zeng B, Wang S, Kang J H, Joshi T, Jin C, Ju L, Kim J, Lyu T, Shen Y, Crommie M, Gao H, Wang F 2016 Nat. Mater. 15 840 Google Scholar
[23]	Yao W, Wang E, Bao C, Zhang Y, Zhang K, Bao K, Zhu J, Chan C K, Chen C, Avilad J, Asensiod M C, Zhou S 2018 Proc. Natl. Acad. Sci. 115 6928 Google Scholar
[24]	Shi H, Zhan Z, Qi Z, Huang K, van Veen E, Silva-Guillén J A, Katsnelson M I, Zhang R, Li P, Xie K, Ji H, Katsnelson, Yuan S, Qin S, Zhang Z 2019 arXiv preprint arXiv: 1905 04515
[25]	Yan C, Ma D L, Qiao J B, Zhong H Y, Yang L, Li S Y, He L 2019 2D Materials 6 045041
[26]	Zhang H, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[27]	Ma Z, Li S, Zheng Y W, Xiao M M, Jiang H, Gao J H, Xie X C 2019 arXiv preprint arXiv: 1905 00622
[28]	Xu X, Yao W, Xiao D, Heinz T F 2014 Nat. Phys. 10 343 Google Scholar
[29]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Firsov A A 2004 Science 306 666 Google Scholar
[30]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197 Google Scholar
[31]	Schedin F, Geim A K, Morozov S V, Hill E W, Blake P, Katsnelson M I, Novoselov K S 2007 Nat. Mater. 6 652 Google Scholar
[32]	Zhang Y, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201 Google Scholar
[33]	Novoselov K S, Jiang Z, Zhang Y, Morozov S V, Stormer H L, Zeitler U, Maan J C, Boebinger G S, Kim P, Geim A K 2007 Science 315 1379 Google Scholar
[34]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[35]	Tse W K, Qiao Z, Yao Y, MacDonald A H, Niu Q 2011 Phys. Rev. B 83 155447 Google Scholar
[36]	Xiao D, Yao W, Niu Q 2007 Phys. Rev. Lett. 99 236809 Google Scholar
[37]	Yao W, Xiao D, Niu Q 2008 Phys. Rev. B 77 235406 Google Scholar
[38]	Jung J, DaSilva A M, MacDonald A H, Adam S 2015 Nat. Commun. 6 6308 Google Scholar
[39]	Song J C, Samutpraphoot P, Levitov L S 2015 Proc. Natl. Acad. Sci. 112 10879 Google Scholar
[40]	Abergel D S, Wallbank J R, Chen X, Mucha-Kruczyński M, Fal'ko V I 2013 New J. Phys. 15 123009 Google Scholar
[41]	Basov D N, Fogler M M, Lanzara A, Wang F, Zhang Y 2014 Rev. Mod. Phys. 86 959 Google Scholar
[42]	Shi Z, Jin C, Yang W, Ju L, Horng J, Lu X, Bechtel H A, Martin M C, Fu D, Wu J, Watanabe K, Taniguchi T, Zhang Y, Bai X, Wang E, Zhang G, Wang F 2014 Nat. Phys. 10 743 Google Scholar
[43]	Yankowitz M, Xue J, LeRoy B J 2014 J. Phys. Condens. Matter 26 303201 Google Scholar
[44]	Gorbachev R V, Song J C W, Yu G L, Kretinin A V, Withers F, Cao Y, Mishchenko A, Grigorieva I V, Novoselov K S, Levitov L S, Geim A K 2014 Science 346 448 Google Scholar
[45]	San-Jose P, Gutiérrez-Rubio A, Sturla M, Guinea F 2014 Phys. Rev. B 90 115152 Google Scholar
[46]	Hunt B, Sanchez-Yamagishi J D, Young A F, Yankowitz M, Taniguchi T, Moon P, Jarillo-Herrero P, Watanabe K, Ashoori R C 2013 Science 340 1427 Google Scholar
[47]	Ponomarenko L A, Gorbachev R V, Yu G L, Elias D C, Jalil R, Patel A A, Mucha-Kruczynski M, Mishchenko A, Mayorov A S, Woods C R, Wallbank J R, Piot B A, Potemski M, Grigorieva I V, Novoselov K S, Guinea F, Fal’ko V I, Geim A K 2013 Nature 497 594 Google Scholar
[48]	Dean C R, Wang L, Maher P, Forsythe C, Ghahari F, Gao Y, Taniguchi T, Katoch J, Ishigami M, Moon P, Koshino M, Watanabe K, Shepard K L, Hone J, Kim P 2013 Nature 497 598 Google Scholar
[49]	Yu G L, Gorbachev R V, Tu J S, Kretinin A V, Cao Y, Jalil R, Withers f, Ponomarenko L A, Piot B A, Potemski M, Chen X, Watanabe K, Taniguchi T, Grigorieva1 I V, Novoselov K S, Fal’ko V I, Geim A K, Mishchenko A Elias D C 2014 Nat. Phys. 10 525 Google Scholar
[50]	Woods C R, Britnell L, Eckmann A, Ma R S, Lu J C, Guo H M, Lin X, Yu G L, Cao Y, Gorbachev R V, Park J, Ponomarenko L A, Katsnelson M L, Gornostyrev Y N, Watanabe K, Taniguchi T, Casiraghi C, H J Gao, Geim A K, Novoselov A K, Kretinin A V 2014 Nat. Phys. 10 451 Google Scholar
[51]	Zhang F, MacDonald A H, Mele E J 2013 Proc. Nat. Acad. Sci. USA 110 10546 Google Scholar
[52]	Li J, Morpurgo A F, Büttiker M, Martin I 2010 Phys. Rev. B 82 245404 Google Scholar
[53]	Li J, Martin I, Büttiker M, Morpurgo A F 2011 Nat. Phys. 7 38 Google Scholar
[54]	Qiao Z, Jung J, Niu Q, MacDonald A H 2011 Nano Lett. 11 3453 Google Scholar
[55]	Jung J, Zhang F, Qiao Z, MacDonald A H 2011 Phys. Rev. B 84 075418 Google Scholar
[56]	Zarenia M, Pereira Jr J M, Farias G A, Peeters F M 2011 Phys. Rev. B 84 125451 Google Scholar
[57]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802 Google Scholar
[58]	Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757 Google Scholar
[59]	Song Y, Dery H 2013 Phys. Rev. Lett. 111 026601 Google Scholar
[60]	Liu G B, Shan W Y, Yao Y, Yao W, Xiao D 2013 Phys. Rev. B 88 085433 Google Scholar
[61]	Jiang B Y, Ni G X, Addison Z, Shi J K, Liu X, Zhao F, Kim P, Mele E J, D N Basov, Fogler M M 2017 Nano Lett. 17 7080 Google Scholar
[62]	Li J, Wang K, McFaul K J, Zern Z, Ren Y, Watanabe K, Taniguchi T, Qiao Z, Zhu J 2016 Nat. Nanotechnol. 11 1060 Google Scholar
[63]	Martin I, Blanter Y M, Morpurgo A F 2008 Phys. Rev. Lett. 100 036804 Google Scholar
[64]	Ju L, Shi Z, Nair N, Lv Y, Jin C, Velasco Jr J, Analytis J, Ojeda-Aristizabal C, Bechtel H A, Martin M C, Zettl A, Analytis J, Wang F 2015 Nature 520 650 Google Scholar
[65]	S S Sunku1, G X Ni, B Y Jiang, H Yoo, A Sternbach, A S McLeod, T Stauber, L Xiong, T Taniguchi, K Watanabe, P Kim, M M Fogler, D N Basov 2018 Science 362 1153 Google Scholar
[66]	Mott N F 1949 Proc. Phys. Soc. London Ser. A 62 416 Google Scholar
[67]	Imada M, Fujimori A, Tokura Y 1998 Rev. Mod. Phys. 70 1039 Google Scholar
[68]	Hubbard J 1964 Phys. R. Soc. A 281 401 Google Scholar
[69]	Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 Google Scholar
[70]	Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. USA 108 12233 Google Scholar
[71]	Sharpe A L, Fox E J, Barnard A W, Finney J, Watanabe K, Taniguchi T, M A Kastner, Goldhaber-Gordon D 2019 arXiv preprint arXiv: 1901 03520
[72]	Koshino M, McCann E 2009 Phys. Rev. B 80 165409 Google Scholar
[73]	Zhang F, Sahu B, Min H, MacDonald A H 2010 Phys. Rev. B 82 035409 Google Scholar
[74]	Bao W, Jing L, Velasco Jr J, Lee Y, Liu G, Tran D, Standley B, Aykol M, Cronin S B, Smirnov D, Koshino M, McCann E, Bockrath M, Lau C N 2011 Nat. Phys. 7 948 Google Scholar
[75]	Lui C H, Li Z, Mak K F, Cappelluti E, Heinz T F 2011 Nat. Phys. 7 944 Google Scholar
[76]	Zhang L, Zhang Y, Camacho J, Khodas M, Zaliznyak I 2011 Nat. Phys. 7 953 Google Scholar
[77]	Yankowitz M, Xue J, Cormode D, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Jarillo-Herrero P, Jacquod P, LeRoy B J 2012 Nat. Phys. 8 382 Google Scholar
[78]	Wallbank J R, Patel A A, Mucha-Kruczyński M, Geim A K, Fal'ko V I 2013 Phys. Rev. B 87 245408 Google Scholar
[79]	Jung J, Raoux A, Qiao Z, MacDonald A H 2014 Phys. Rev. B 89 205414 Google Scholar
[80]	Ni G X, Wang H, Wu J S, Fei Z, Goldflam M D, Keilmann F, Özyilmaz B, Castro Neto A H, Xie X M, Fogler M M, Basov D N 2015 Nat. Mater. 14 1217 Google Scholar
[81]	Basov D N, Fogler M M, De Abajo F G 2016 Science 354 6309
[82]	段嘉华, 陈佳宁 2019 68 110701 Duan J H, Chen J N 2019 Acta Phys. Sin. 68 110701
[83]	Qazilbash M M, Brehm M, Chae B G, Ho P C, Andreev G O, Kim B J, Yun S J, Balatsky A V, Maple M B, Keilmann F, Kim H T 2007 Science 318 1750 Google Scholar
[84]	Fei Z, Rodin A S, Andreev G O, Bao W, McLeod A S, Wagner M, Zhang L M, Zhao Z, Thiemens M, Dominguez G, Fogler M M, Castro-Neto A H, Lau C N, Keilmann F, Basov D N 2012 Nature 487 82 Google Scholar
[85]	Chen J, Badioli M, Alonso-González P, Thongrattanasiri S, Huth F, Osmond J, Spasenović M, Centeno A, Pesquera A, Godignon P, Zurutuza A, Camara N, Abajo J G, Hillenbrand R, Koppens F 2012 Nature 487 77 Google Scholar
[86]	Woessner A, Lundeberg M B, Gao Y, Principi A, Alonso-González P, Carrega M, Watanabe K, Taniguchi T, Vignale G, Polini M, Hone J, Hillenbrand R, Koppens F H L 2015 Nat. Mater. 14 421 Google Scholar
[87]	Alden J S, Tsen A W, Huang P Y, Hovden R, Brown L, Park J, Muller D A, McEuen P L 2013 Proc. Natl. Acad. Sci. USA 110 11256 Google Scholar
[88]	Fei Z, Rodin A S, Gannett W, Dai S, Regan W, Wagner M, Liu M K, McLeod A S, Dominguez G, Thiemens M, Castro Neto A H, Keilmann F, Zettl A, Hillenbrand R, Fogler M M, Basov D N 2013 Nat. Nanotechnol. 8 821 Google Scholar

施引文献

图 1 (a) 石墨烯、单层过渡金属硫族化合物(TMDs)等材料的二维蜂窝晶格; (b)当单层石墨烯与h-BN基底产生相互作用, 空间反演对称性就会被破坏, 单层TMDs不具有空间反演对称性结构, 在双层石墨烯和双层TMDs中反演对称性可以通过施加z方向的电场打开或关闭; (c) 反演对称性破缺的狄拉克体系在能谷处打开能隙, 箭头表示能谷光学跃迁, 圆形箭头表示不同的圆偏振光^[28]

Fig. 1. (a) 2D hexagonal lattice, representing graphene, monolayer transition metal dichalcogenides (TMDs), etc; (b) In monolayer graphene, inversion symmetry is broken when monolayer graphene interacts with h-BN substrate. The monolayer TMDs have structures that lack inversion symmetry. Inversion symmetry in bilayer graphene and TMDs can be switched on/off by an electric field applied in the z-direction; (c) An energy gap is opened in Dirac systems with broken inversion symmetry. The arrows indicate interband transitions at different valleys, and the circular arrows represent different circularly polarized light^[28].

下载: 全尺寸图片幻灯片

图 2 (a) 双层石墨烯中剪切型畴壁的示意图与BA、鞍点(Saddle point, SP)和AB堆叠的能带结构. 红色和粉色的箭头表示束缚在畴壁上的手性拓扑模; (b), (c) 在正(负)层间偏压${V_{\rm{i}}}$作用下K谷畴壁的能带结构^[61]

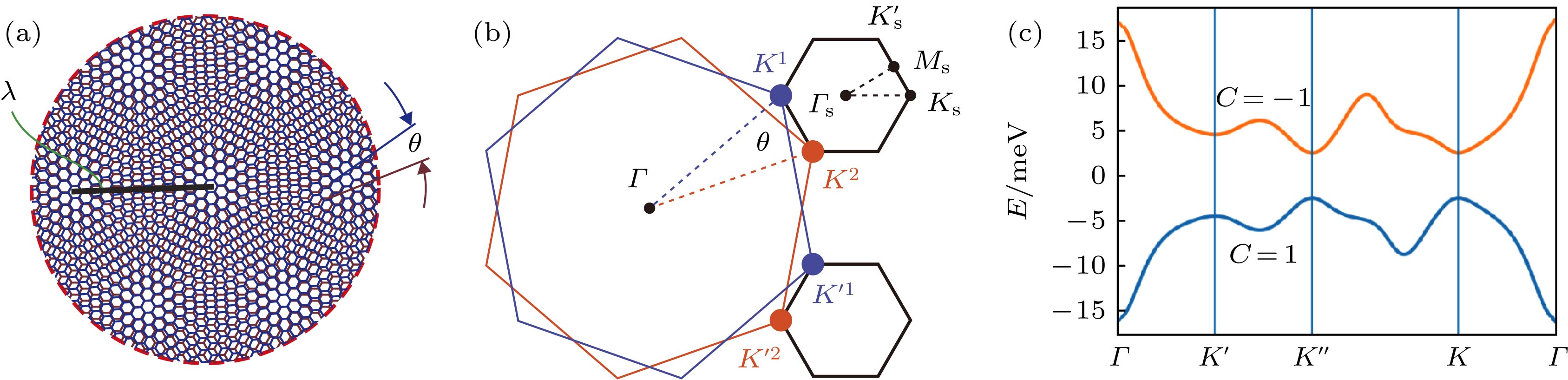
Fig. 2. (a) Schematic representation of a shear domain wall in bilayer graphene and the band structure of BA, Saddle point (SP), and AB stacking. Red and magenta wavy arrows represent chiral topological modes bound to the domain wall; (b), (c) Band structure of the wall under a positive (negative) interlayer bias ${V_{\rm{i}}}$ for the K valley^[61].

下载: 全尺寸图片幻灯片

图 3 (a)转角双层石墨烯莫尔超晶格示意图^[10]; (b)小布里渊区示意图, ${K_{\rm{s}}}$, ${K'_{\rm{s}}}$和${\varGamma _{\rm{s}}}$代表小布里渊区中的点^[10]; (c)与h-BN对齐的转角双层石墨烯中小能带处的能带结构, ${\theta _{\rm{M}}} = 1.20^\circ $^[8]

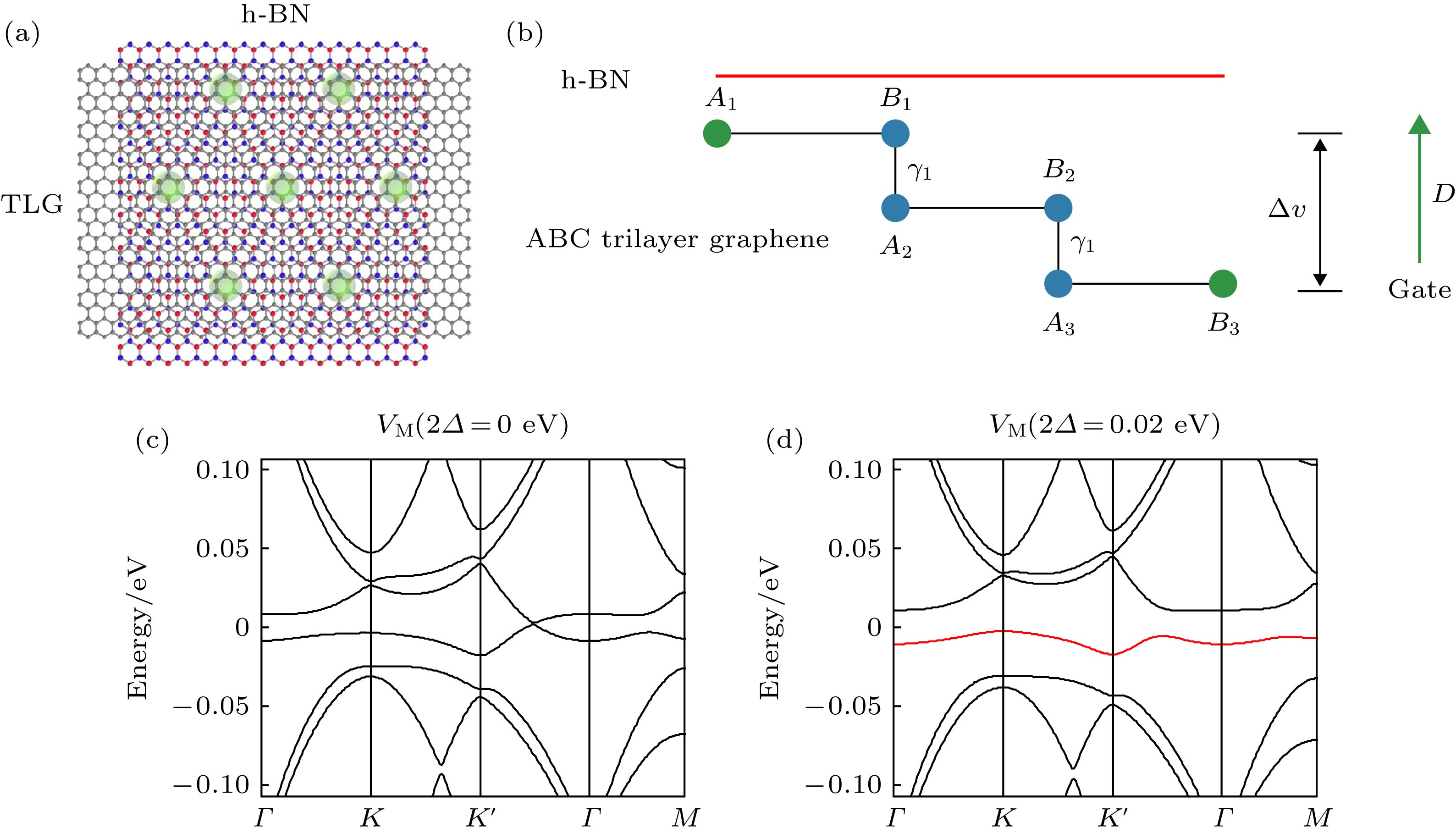
Fig. 3. (a) The Moiré superlattice as seen in twisted bilayer graphene^[10]; (b) schematic representation of the mini Brillouin zone. ${K_{\rm{s}}}$, ${K'_{\rm{s}}}$ and ${\varGamma _{\rm{s}}}$ denote points in the mini Brillouin zone^[10]; (c) band structure for valley + of the twisted bilayer graphene aligned with h-BN in the mini Brillouin zone ${\theta _{\rm{M}}} = 1.20^\circ $^[8].

下载: 全尺寸图片幻灯片

图 4 (a) ABC TLG/h-BN的莫尔超晶格示意图, 为了图像清晰, 只显示了顶部h-BN和底部石墨烯最上层的原子^[13]; (b) ABC堆叠三层石墨烯/h-BN体系示意图, 垂直电场使顶部和底部石墨烯层之间的电子能量差为$\Delta V$^[12]; (c), (d)分别为没有和有垂直电场时的小布里渊区处的能带图; (d)垂直电场在顶部和底部石墨烯层之间产生20 mev的电位差, 导致了一个带宽减小的孤立的空穴型小能带, 增强了强关联作用, 从而生成了可调节的Mott绝缘体态^[13]

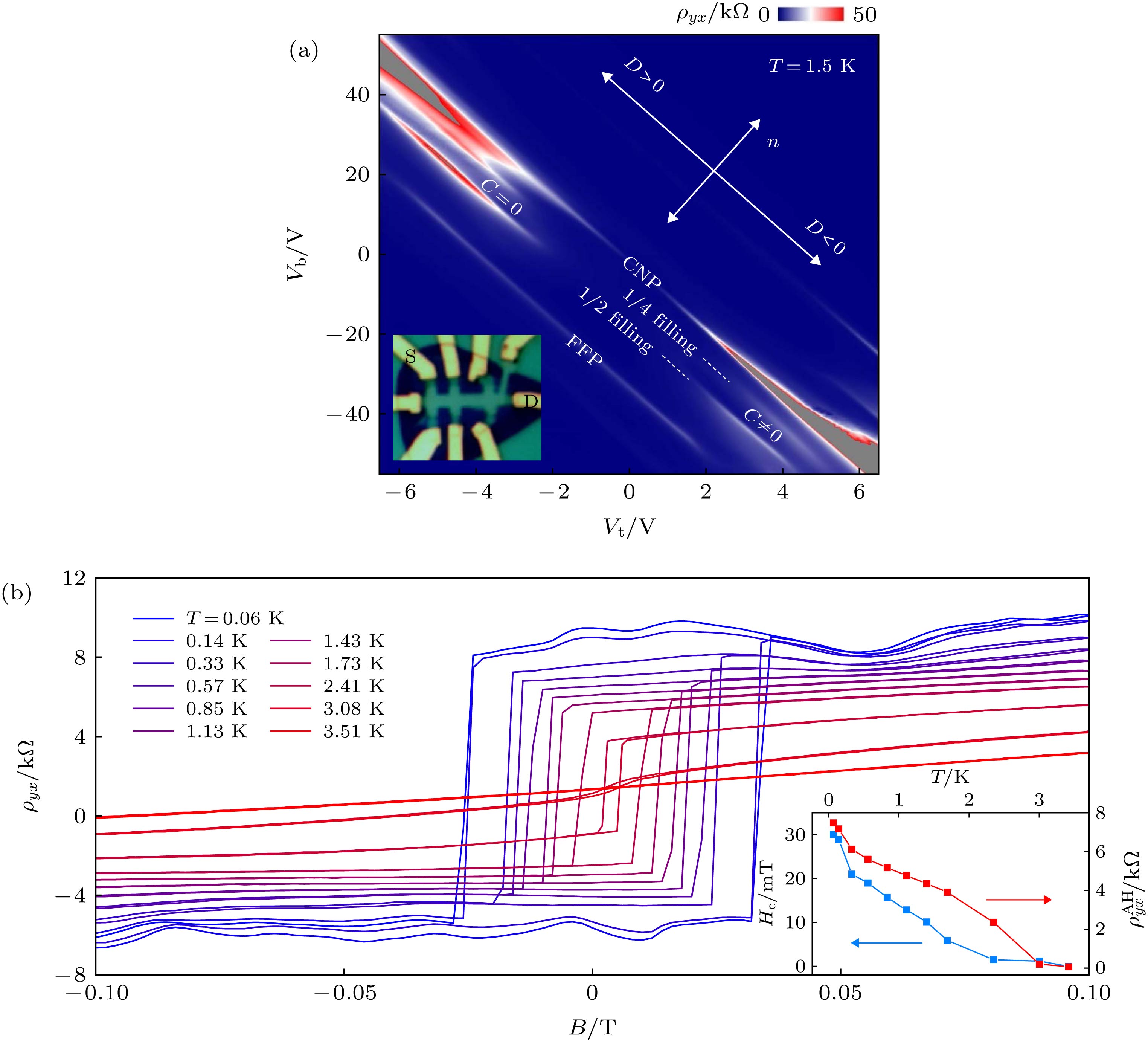
Fig. 4. (a) Schematic of ABC TLG/h-BN Moiré superlattice. Only atoms of the top h-BN layer and the bottom graphene layer are shown for clarity^[13]; (b) illustration of the ABC stacked trilayer graphene/h-BN system. A vertical electric field introduces an energy difference $\varDelta V$ for electrons between the top and the bottom graphene layer^[12]; (c), (d) energy dispersion of the two electron and hole minibands without and with a vertical electrical field, respectively. The vertical electrical field in (d) generates a potential difference of 20 meV between the top and bottom graphene layers, leading to an isolated hole minibands with strongly suppressed bandwidth. The reduced electronic bandwidth relative to the Coulomb interaction enhances the electron correlation, and leads to the tunable Mott insulator states^[13].

下载: 全尺寸图片幻灯片

图 5 ABC TLG/h-BN, 纵向电阻率图和不同磁场下的霍尔电阻率图　(a) T = 1.5 K时以${V_{\rm{t}}}$和${V_{\rm{b}}}$为函数的纵向电阻率图, 箭头分别表示掺杂(n)和电位移场(D)的方向. 理论预言D < 0时空穴小能带为拓扑非平庸态(即陈数C ≠ 0), D > 0时为拓扑平庸态(C = 0); (b)在1/4填充和D = –0.5 V/nm时不同的温度下的霍尔电阻${\rho _{yx}}$, 显示出清晰的反常霍尔效应(AH)的信号并伴随着很强的磁滞回线. 在温度T = 0.06 K时, 横向电阻$\rho _{yx}^{{\rm{AH}}} = 8\;{\rm{k}}\Omega $和矫顽场${H_{\rm{c}}} = 30\;{\rm{mT}}$. 插图: 矫顽场和AH信号与温度的函数^[14]

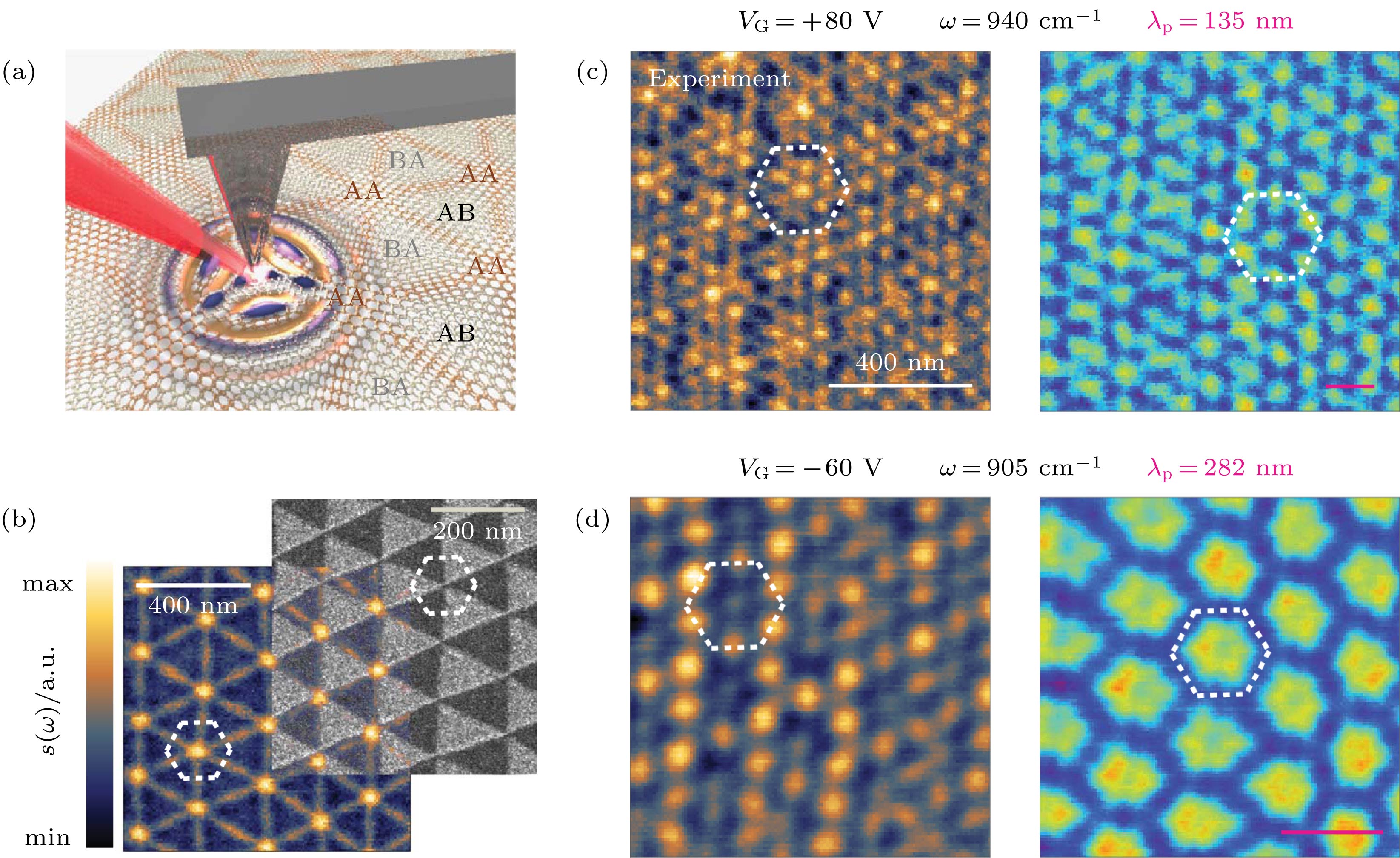
Fig. 5. ABC TLG/h-BN, color plot of the longitudinal resistivity and Magnetic field dependent ${\rho _{yx}}$: (a) Longitudinal resistivity as a function of ${V_{\rm{t}}}$ and ${V_{\rm{b}}}$ at T = 1.5 K. The arrows show the direction of changing doping (n) and displacement field (D), respectively. It was predicted theoretically that the hole miniband is topological (Chern number C ≠ 0) for D < 0 and trivial (C = 0) for D > 0; (b) magnetic field dependent ${\rho _{yx}}$ at 1/4 filling and D = –0.5 V/nm at different temperatures. The Hall resistivity displays a clear AH signal with strong ferromagnetic hysteresis. At the base temperature of T = 0.06 K, the AH signal can be as high as $\rho _{yx}^{{\rm{AH}}} = 8\;{\rm{k}}\Omega $ and the coercive field is ${H_{\rm{c}}} = 30\;{\rm{mT}}$. Inset: Extracted coercive field ${H_{\rm{c}}}$ and AH signal $\rho _{yx}^{{\rm{AH}}}$ as a function of temperature^[14]

下载: 全尺寸图片幻灯片

图 6 (a) 红外s-SNOM实验技术示意图. AB、BA和AA表示双层石墨烯堆积方式的周期性改变; (b) (左)显示转角双层石墨烯中由畴壁晶格形成的纳米光子晶体. 这种反差是由于畴壁的局部光学导电性增强造成的. (右)转角双层石墨烯样品的暗场TEM图像; (c), (d) 分别为${\lambda _{\rm{p}}}$ = 135 nm和282 nm时获得的红外s-SNOM图像^[65]

Fig. 6. (a) Schematic of the IR s-SNOM experimental technique. AB, BA, and AA label periodically occurring stacking types of graphene layers; (b) (Left) isualizing the nano-light photonic crystal formed by the domain wall in twisted bilayer graphene. The contrast is due to enhanced local optical conductivity at domain wall. (Right) Dark-field TEM image of a twisted bilayer graphene sample; (c), (d) IR s-SNOM images obtained for ${\lambda _{\rm{p}}}$ = 135 nm and 282 nm, respectively^[65].

下载: 全尺寸图片幻灯片

图 7 (a) 通过唯象模型得到的石墨烯/h-BN电子能带结构的三维表示; (b) ${E_{\rm{F}}}$小于${E_\mu }$~170 meV时的光学跃迁; (c) ${E_{\rm{F}}}$大于${E_\mu }$时莫尔势导致多个额外的光学跃迁通道, 这些跃迁提高电导率, 同时对等离激元波长产生了一个额外的带间跃迁贡献^[80]

Fig. 7. (a) 3D representation of the electronic band structure of graphene/h-BN obtained from the phenomenological model; (b) Optical transitions at 170 mev, for a magnitude of the ${E_{\rm{F}}}$ smaller than ${E_{\rm{\mu }}}$; (c) For a magnitude of ${E_{\rm{F}}}$ larger than ${E_\mu }$ one finds multiple additional channels for optical transitions, all initiated by the moirépotential. These transitions enhance the conductivity and also yield an interband contribution to the plasmonic wavelength in addition to intraband contribution^[80].

下载: 全尺寸图片幻灯片

图 8 不同载流子密度下莫尔石墨烯和普通石墨烯的等离激元谱线^[80]　(a) 0.8 × 10 ¹²cm^–2; (b) 2.9 × 10¹²cm^–2

Fig. 8. Plasmonic line-profiles for both Moiré graphene and plain graphene at different carrier densities^[80]: (a) 0.8 × 10¹² cm^–2; (b) 2.9 × 10¹² cm^–2.

下载: 全尺寸图片幻灯片

map

[1]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[2]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[3]	Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405 Google Scholar
[4]	Wang Z J, Sun Y, Chen X Q, Franchini C, Xu G, Weng H M, Dai X, Fang Z 2012 Phys. Rev. B 85 195320 Google Scholar
[5]	Wang Z J, Weng H M, Wu Q S, Dai X, Fang Z 2013 Phys. Rev. B 88 125427 Google Scholar
[6]	Weng H M, Fang C, Fang Z, Bernrviget B A, Dai X 2015 Phys. Rev. X 5 011029
[7]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[8]	Zhang Y H, Mao D, Senthil T 2019 arXiv preprint arXiv: 1901 08209
[9]	Bultinck N, Chatterjee S, Zaletel M P 2019 arXiv preprint arXiv: 1901 08110
[10]	Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, P Jarillo-Herrero, Ashoori R C 2018 Nature 556 80 Google Scholar
[11]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[12]	Zhang Y H, Senthil T 2019 Phys. Rev. B 99 205150 Google Scholar
[13]	Chen G, Jiang L, Wu S, Lyu B, Li H, Chittari B L, Kenji W, Takashi T, Shi Z, Jeil J, Zhang Y, Wang F 2019 Nat. Phys. 15 237 Google Scholar
[14]	Chen G, Sharpe A L, Fox E J, Zhang Y H, Wang S, Jiang L, Lyu B, Watanabe K, Takashi T, Senthil T, David G G, Shi Z, Wang F 2019 arXiv preprint arXiv: 1905 06535
[15]	Chittari B L, Chen G, Zhang Y, Wang F, Jung J 2019 Phys. Rev. Lett. 122 016401 Google Scholar
[16]	Liu X, Hao Z, Khalaf E, Lee J Y, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2019 arXiv preprint arXiv: 1903 08130
[17]	Cao Y, Rodan-Legrain D, Rubies-Bigordà O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2019 arXiv preprint arXiv: 1903.08596
[18]	Shen C, Li N, Wang S, Zhao Y, Tang J, Liu J, Tian J, Chu Y, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D, Zhang G 2019 arXiv preprint arXiv: 1903 06952
[19]	Koshino M 2019 Phys. Rev. B 99 235406 Google Scholar
[20]	Chen Z G, Shi Z, Yang W, Lu X, Lai Y, Yan H, Yan H, Zhang G, Li Z 2014 Nat. Commun. 5 4461 Google Scholar
[21]	Wu S, Wang L, Lai Y, Shan W Y, Aivazian G, Zhang X, Taniguchi T, Watanabe K J, Xiao D, Dean C, Hone J, Li Z, Xu X 2016 Sci. Adv. 2 e1600002 Google Scholar
[22]	Jiang L, Shi Z, Zeng B, Wang S, Kang J H, Joshi T, Jin C, Ju L, Kim J, Lyu T, Shen Y, Crommie M, Gao H, Wang F 2016 Nat. Mater. 15 840 Google Scholar
[23]	Yao W, Wang E, Bao C, Zhang Y, Zhang K, Bao K, Zhu J, Chan C K, Chen C, Avilad J, Asensiod M C, Zhou S 2018 Proc. Natl. Acad. Sci. 115 6928 Google Scholar
[24]	Shi H, Zhan Z, Qi Z, Huang K, van Veen E, Silva-Guillén J A, Katsnelson M I, Zhang R, Li P, Xie K, Ji H, Katsnelson, Yuan S, Qin S, Zhang Z 2019 arXiv preprint arXiv: 1905 04515
[25]	Yan C, Ma D L, Qiao J B, Zhong H Y, Yang L, Li S Y, He L 2019 2D Materials 6 045041
[26]	Zhang H, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[27]	Ma Z, Li S, Zheng Y W, Xiao M M, Jiang H, Gao J H, Xie X C 2019 arXiv preprint arXiv: 1905 00622
[28]	Xu X, Yao W, Xiao D, Heinz T F 2014 Nat. Phys. 10 343 Google Scholar
[29]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Firsov A A 2004 Science 306 666 Google Scholar
[30]	Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A A 2005 Nature 438 197 Google Scholar
[31]	Schedin F, Geim A K, Morozov S V, Hill E W, Blake P, Katsnelson M I, Novoselov K S 2007 Nat. Mater. 6 652 Google Scholar
[32]	Zhang Y, Tan Y W, Stormer H L, Kim P 2005 Nature 438 201 Google Scholar
[33]	Novoselov K S, Jiang Z, Zhang Y, Morozov S V, Stormer H L, Zeitler U, Maan J C, Boebinger G S, Kim P, Geim A K 2007 Science 315 1379 Google Scholar
[34]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[35]	Tse W K, Qiao Z, Yao Y, MacDonald A H, Niu Q 2011 Phys. Rev. B 83 155447 Google Scholar
[36]	Xiao D, Yao W, Niu Q 2007 Phys. Rev. Lett. 99 236809 Google Scholar
[37]	Yao W, Xiao D, Niu Q 2008 Phys. Rev. B 77 235406 Google Scholar
[38]	Jung J, DaSilva A M, MacDonald A H, Adam S 2015 Nat. Commun. 6 6308 Google Scholar
[39]	Song J C, Samutpraphoot P, Levitov L S 2015 Proc. Natl. Acad. Sci. 112 10879 Google Scholar
[40]	Abergel D S, Wallbank J R, Chen X, Mucha-Kruczyński M, Fal'ko V I 2013 New J. Phys. 15 123009 Google Scholar
[41]	Basov D N, Fogler M M, Lanzara A, Wang F, Zhang Y 2014 Rev. Mod. Phys. 86 959 Google Scholar
[42]	Shi Z, Jin C, Yang W, Ju L, Horng J, Lu X, Bechtel H A, Martin M C, Fu D, Wu J, Watanabe K, Taniguchi T, Zhang Y, Bai X, Wang E, Zhang G, Wang F 2014 Nat. Phys. 10 743 Google Scholar
[43]	Yankowitz M, Xue J, LeRoy B J 2014 J. Phys. Condens. Matter 26 303201 Google Scholar
[44]	Gorbachev R V, Song J C W, Yu G L, Kretinin A V, Withers F, Cao Y, Mishchenko A, Grigorieva I V, Novoselov K S, Levitov L S, Geim A K 2014 Science 346 448 Google Scholar
[45]	San-Jose P, Gutiérrez-Rubio A, Sturla M, Guinea F 2014 Phys. Rev. B 90 115152 Google Scholar
[46]	Hunt B, Sanchez-Yamagishi J D, Young A F, Yankowitz M, Taniguchi T, Moon P, Jarillo-Herrero P, Watanabe K, Ashoori R C 2013 Science 340 1427 Google Scholar
[47]	Ponomarenko L A, Gorbachev R V, Yu G L, Elias D C, Jalil R, Patel A A, Mucha-Kruczynski M, Mishchenko A, Mayorov A S, Woods C R, Wallbank J R, Piot B A, Potemski M, Grigorieva I V, Novoselov K S, Guinea F, Fal’ko V I, Geim A K 2013 Nature 497 594 Google Scholar
[48]	Dean C R, Wang L, Maher P, Forsythe C, Ghahari F, Gao Y, Taniguchi T, Katoch J, Ishigami M, Moon P, Koshino M, Watanabe K, Shepard K L, Hone J, Kim P 2013 Nature 497 598 Google Scholar
[49]	Yu G L, Gorbachev R V, Tu J S, Kretinin A V, Cao Y, Jalil R, Withers f, Ponomarenko L A, Piot B A, Potemski M, Chen X, Watanabe K, Taniguchi T, Grigorieva1 I V, Novoselov K S, Fal’ko V I, Geim A K, Mishchenko A Elias D C 2014 Nat. Phys. 10 525 Google Scholar
[50]	Woods C R, Britnell L, Eckmann A, Ma R S, Lu J C, Guo H M, Lin X, Yu G L, Cao Y, Gorbachev R V, Park J, Ponomarenko L A, Katsnelson M L, Gornostyrev Y N, Watanabe K, Taniguchi T, Casiraghi C, H J Gao, Geim A K, Novoselov A K, Kretinin A V 2014 Nat. Phys. 10 451 Google Scholar
[51]	Zhang F, MacDonald A H, Mele E J 2013 Proc. Nat. Acad. Sci. USA 110 10546 Google Scholar
[52]	Li J, Morpurgo A F, Büttiker M, Martin I 2010 Phys. Rev. B 82 245404 Google Scholar
[53]	Li J, Martin I, Büttiker M, Morpurgo A F 2011 Nat. Phys. 7 38 Google Scholar
[54]	Qiao Z, Jung J, Niu Q, MacDonald A H 2011 Nano Lett. 11 3453 Google Scholar
[55]	Jung J, Zhang F, Qiao Z, MacDonald A H 2011 Phys. Rev. B 84 075418 Google Scholar
[56]	Zarenia M, Pereira Jr J M, Farias G A, Peeters F M 2011 Phys. Rev. B 84 125451 Google Scholar
[57]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802 Google Scholar
[58]	Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757 Google Scholar
[59]	Song Y, Dery H 2013 Phys. Rev. Lett. 111 026601 Google Scholar
[60]	Liu G B, Shan W Y, Yao Y, Yao W, Xiao D 2013 Phys. Rev. B 88 085433 Google Scholar
[61]	Jiang B Y, Ni G X, Addison Z, Shi J K, Liu X, Zhao F, Kim P, Mele E J, D N Basov, Fogler M M 2017 Nano Lett. 17 7080 Google Scholar
[62]	Li J, Wang K, McFaul K J, Zern Z, Ren Y, Watanabe K, Taniguchi T, Qiao Z, Zhu J 2016 Nat. Nanotechnol. 11 1060 Google Scholar
[63]	Martin I, Blanter Y M, Morpurgo A F 2008 Phys. Rev. Lett. 100 036804 Google Scholar
[64]	Ju L, Shi Z, Nair N, Lv Y, Jin C, Velasco Jr J, Analytis J, Ojeda-Aristizabal C, Bechtel H A, Martin M C, Zettl A, Analytis J, Wang F 2015 Nature 520 650 Google Scholar
[65]	S S Sunku1, G X Ni, B Y Jiang, H Yoo, A Sternbach, A S McLeod, T Stauber, L Xiong, T Taniguchi, K Watanabe, P Kim, M M Fogler, D N Basov 2018 Science 362 1153 Google Scholar
[66]	Mott N F 1949 Proc. Phys. Soc. London Ser. A 62 416 Google Scholar
[67]	Imada M, Fujimori A, Tokura Y 1998 Rev. Mod. Phys. 70 1039 Google Scholar
[68]	Hubbard J 1964 Phys. R. Soc. A 281 401 Google Scholar
[69]	Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 Google Scholar
[70]	Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. USA 108 12233 Google Scholar
[71]	Sharpe A L, Fox E J, Barnard A W, Finney J, Watanabe K, Taniguchi T, M A Kastner, Goldhaber-Gordon D 2019 arXiv preprint arXiv: 1901 03520
[72]	Koshino M, McCann E 2009 Phys. Rev. B 80 165409 Google Scholar
[73]	Zhang F, Sahu B, Min H, MacDonald A H 2010 Phys. Rev. B 82 035409 Google Scholar
[74]	Bao W, Jing L, Velasco Jr J, Lee Y, Liu G, Tran D, Standley B, Aykol M, Cronin S B, Smirnov D, Koshino M, McCann E, Bockrath M, Lau C N 2011 Nat. Phys. 7 948 Google Scholar
[75]	Lui C H, Li Z, Mak K F, Cappelluti E, Heinz T F 2011 Nat. Phys. 7 944 Google Scholar
[76]	Zhang L, Zhang Y, Camacho J, Khodas M, Zaliznyak I 2011 Nat. Phys. 7 953 Google Scholar
[77]	Yankowitz M, Xue J, Cormode D, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Jarillo-Herrero P, Jacquod P, LeRoy B J 2012 Nat. Phys. 8 382 Google Scholar
[78]	Wallbank J R, Patel A A, Mucha-Kruczyński M, Geim A K, Fal'ko V I 2013 Phys. Rev. B 87 245408 Google Scholar
[79]	Jung J, Raoux A, Qiao Z, MacDonald A H 2014 Phys. Rev. B 89 205414 Google Scholar
[80]	Ni G X, Wang H, Wu J S, Fei Z, Goldflam M D, Keilmann F, Özyilmaz B, Castro Neto A H, Xie X M, Fogler M M, Basov D N 2015 Nat. Mater. 14 1217 Google Scholar
[81]	Basov D N, Fogler M M, De Abajo F G 2016 Science 354 6309
[82]	段嘉华, 陈佳宁 2019 68 110701 Duan J H, Chen J N 2019 Acta Phys. Sin. 68 110701
[83]	Qazilbash M M, Brehm M, Chae B G, Ho P C, Andreev G O, Kim B J, Yun S J, Balatsky A V, Maple M B, Keilmann F, Kim H T 2007 Science 318 1750 Google Scholar
[84]	Fei Z, Rodin A S, Andreev G O, Bao W, McLeod A S, Wagner M, Zhang L M, Zhao Z, Thiemens M, Dominguez G, Fogler M M, Castro-Neto A H, Lau C N, Keilmann F, Basov D N 2012 Nature 487 82 Google Scholar
[85]	Chen J, Badioli M, Alonso-González P, Thongrattanasiri S, Huth F, Osmond J, Spasenović M, Centeno A, Pesquera A, Godignon P, Zurutuza A, Camara N, Abajo J G, Hillenbrand R, Koppens F 2012 Nature 487 77 Google Scholar
[86]	Woessner A, Lundeberg M B, Gao Y, Principi A, Alonso-González P, Carrega M, Watanabe K, Taniguchi T, Vignale G, Polini M, Hone J, Hillenbrand R, Koppens F H L 2015 Nat. Mater. 14 421 Google Scholar
[87]	Alden J S, Tsen A W, Huang P Y, Hovden R, Brown L, Park J, Muller D A, McEuen P L 2013 Proc. Natl. Acad. Sci. USA 110 11256 Google Scholar
[88]	Fei Z, Rodin A S, Gannett W, Dai S, Regan W, Wagner M, Liu M K, McLeod A S, Dominguez G, Thiemens M, Castro Neto A H, Keilmann F, Zettl A, Hillenbrand R, Fogler M M, Basov D N 2013 Nat. Nanotechnol. 8 821 Google Scholar

[1]	刘钊. 莫尔超晶格中的分数化拓扑量子态. , 2024, 73(20): 207303. doi: 10.7498/aps.73.20241029
[2]	郭瑞平, 俞弘毅. 二维半导体莫尔超晶格中随位置与动量变化的层间耦合. , 2023, 72(2): 027302. doi: 10.7498/aps.72.20222046
[3]	吴泽飞, 黄美珍, 王宁. 二维莫尔超晶格中的非线性霍尔效应. , 2023, 72(23): 237301. doi: 10.7498/aps.72.20231324
[4]	徐琨淇, 胡成, 沈沛约, 马赛群, 周先亮, 梁齐, 史志文. 叠层/转角二维原子晶体结构与极化激元的近场光学表征. , 2023, 72(2): 027102. doi: 10.7498/aps.72.20222145
[5]	李听昕. 二维范德瓦耳斯半导体莫尔超晶格实验研究进展. , 2022, 71(12): 127309. doi: 10.7498/aps.71.20220347
[6]	方静云, 孙庆丰. 石墨烯p-n结在磁场中的电输运热耗散. , 2022, 71(12): 127203. doi: 10.7498/aps.71.20220029
[7]	詹真, 张亚磊, 袁声军. 石墨烯莫尔超晶格的晶格弛豫与衬底效应. , 2022, 71(18): 187302. doi: 10.7498/aps.71.20220872
[8]	李海鹏, 周佳升, 吉炜, 杨自强, 丁慧敏, 张子韬, 沈晓鹏, 韩奎. 边界对石墨烯量子点非线性光学性质的影响. , 2021, 70(5): 057801. doi: 10.7498/aps.70.20201643
[9]	王波, 张纪红, 李聪颖. 石墨烯增强半导体态二氧化钒近场热辐射. , 2021, 70(5): 054207. doi: 10.7498/aps.70.20201360
[10]	岑贵, 张志斌, 吕新宇, 刘开辉, 李志强. 金属衬底上石墨烯的红外近场光学. , 2020, 69(2): 027803. doi: 10.7498/aps.69.20191598
[11]	李小兵, 陆卫兵, 刘震国, 陈昊. 基于可调石墨烯超表面的宽角度动态波束控制. , 2018, 67(18): 184101. doi: 10.7498/aps.67.20180592
[12]	闫昕, 梁兰菊, 张璋, 杨茂生, 韦德泉, 王猛, 李院平, 吕依颖, 张兴坊, 丁欣, 姚建铨. 基于石墨烯编码超构材料的太赫兹波束多功能动态调控. , 2018, 67(11): 118102. doi: 10.7498/aps.67.20180125
[13]	王越, 冷雁冰, 王丽, 董连和, 刘顺瑞, 王君, 孙艳军. 基于石墨烯振幅可调的宽带类电磁诱导透明超材料设计. , 2018, 67(9): 097801. doi: 10.7498/aps.67.20180114
[14]	张银, 冯一军, 姜田, 曹杰, 赵俊明, 朱博. 基于石墨烯的太赫兹波散射可调谐超表面. , 2017, 66(20): 204101. doi: 10.7498/aps.66.204101
[15]	贾子源, 杨玉婷, 季立宇, 杭志宏. 类石墨烯复杂晶胞光子晶体中的确定性界面态. , 2017, 66(22): 227802. doi: 10.7498/aps.66.227802
[16]	张会云, 黄晓燕, 陈琦, 丁春峰, 李彤彤, 吕欢欢, 徐世林, 张晓, 张玉萍, 姚建铨. 基于石墨烯互补超表面的可调谐太赫兹吸波体. , 2016, 65(1): 018101. doi: 10.7498/aps.65.018101
[17]	金芹, 董海明, 韩奎, 王雪峰. 石墨烯超快动态光学性质. , 2015, 64(23): 237801. doi: 10.7498/aps.64.237801
[18]	卢晓波, 张广宇. 石墨烯莫尔超晶格. , 2015, 64(7): 077305. doi: 10.7498/aps.64.077305
[19]	黄向前, 林陈昉, 尹秀丽, 赵汝光, 王恩哥, 胡宗海. 一维石墨烯超晶格上的氢吸附. , 2014, 63(19): 197301. doi: 10.7498/aps.63.197301
[20]	董海明. 掺杂石墨烯系统电场调控的非线性太赫兹光学特性研究. , 2013, 62(23): 237804. doi: 10.7498/aps.62.237804

计量

文章访问数: 23261
PDF下载量: 1171
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

石墨烯莫尔超晶格体系的拓扑性质及光学研究进展