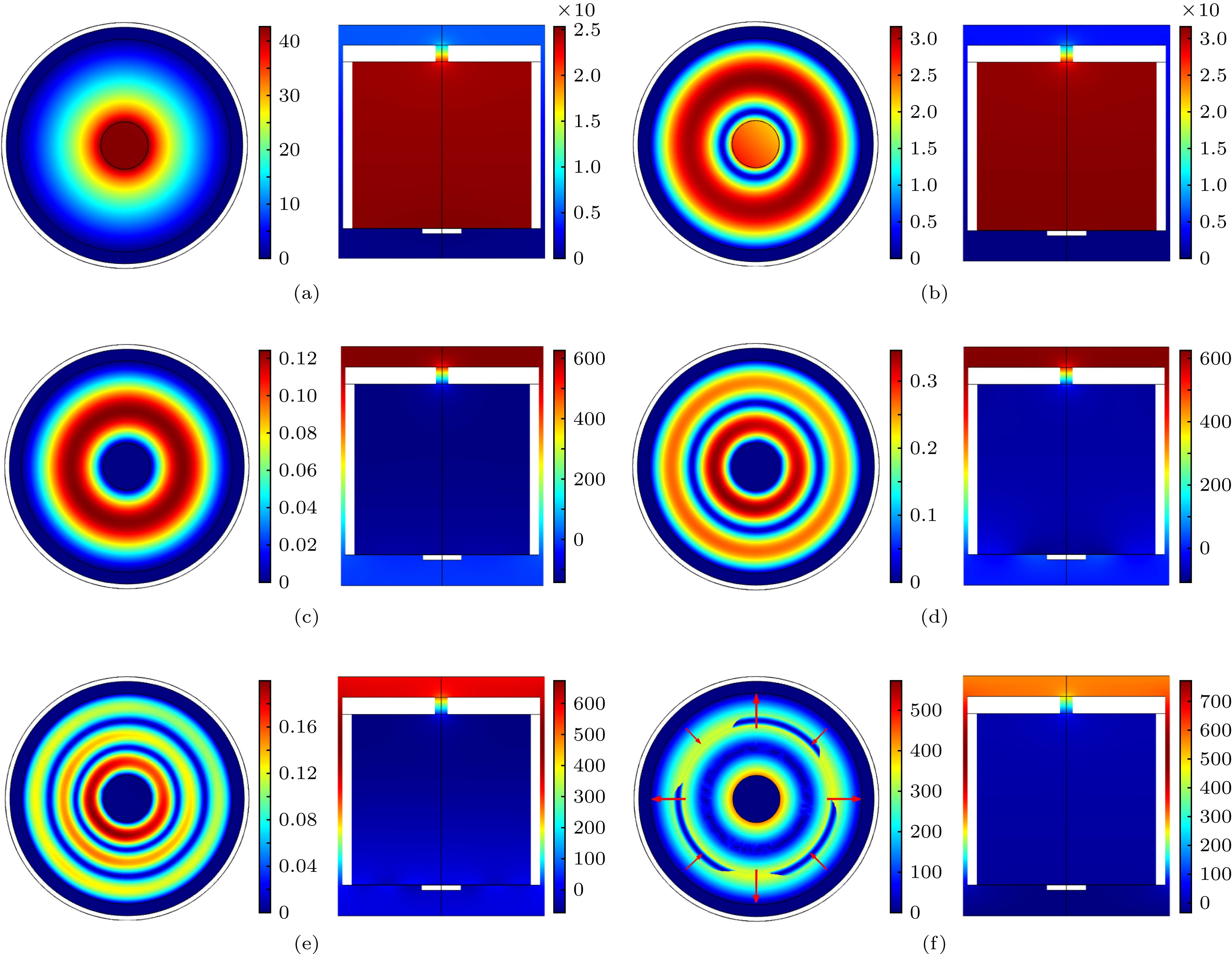
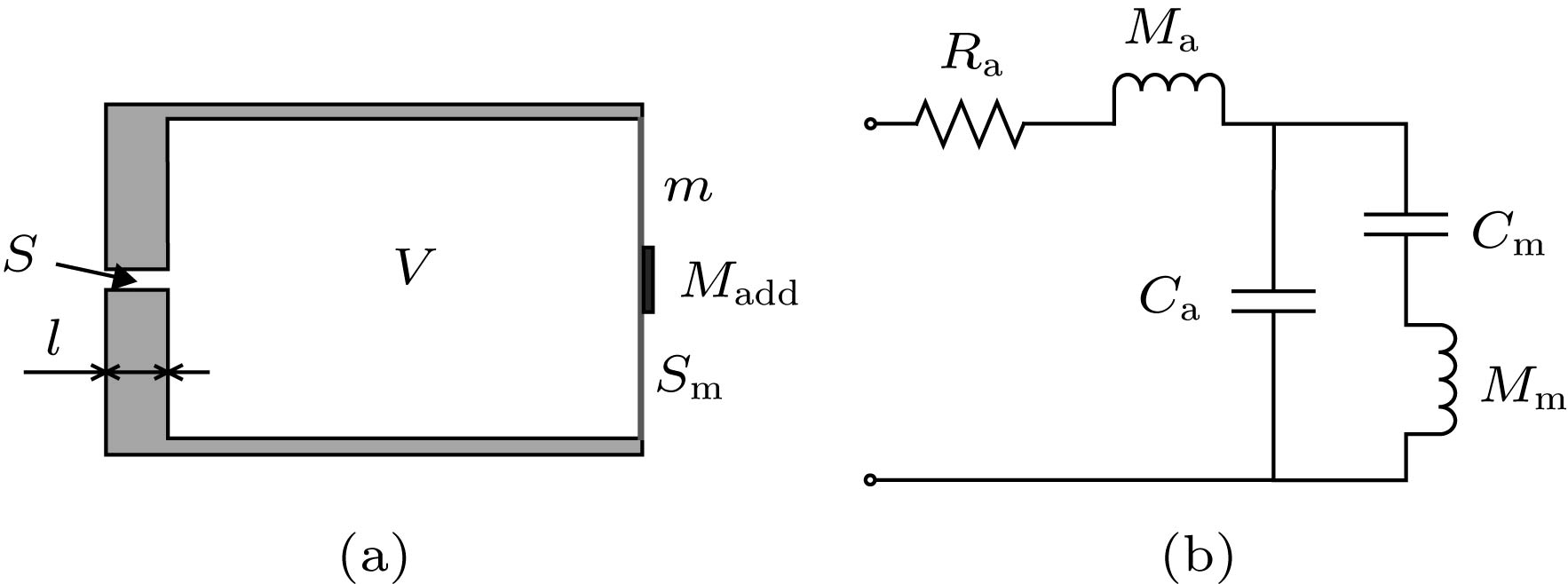
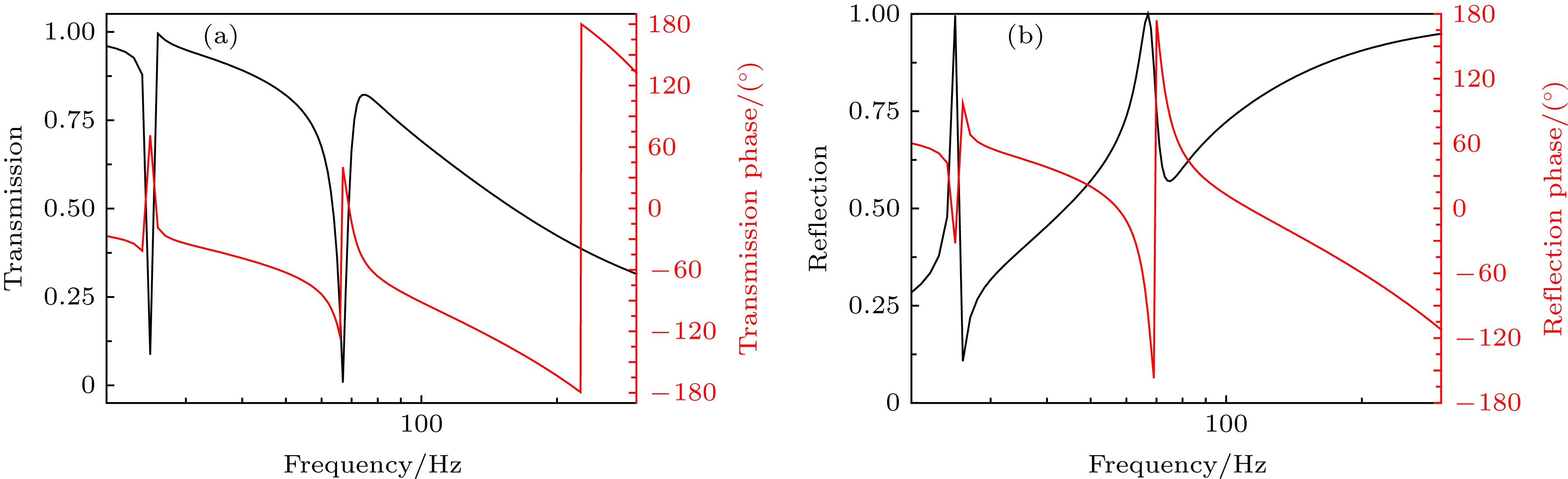
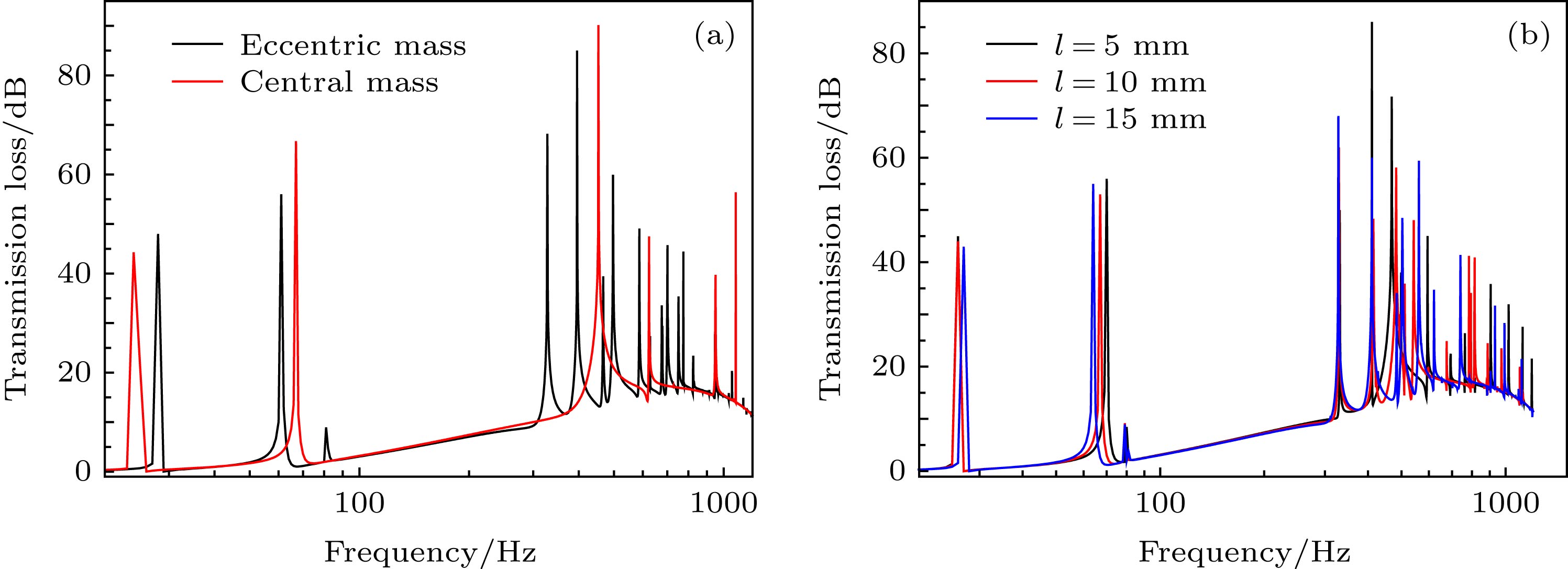
-
针对低频噪声的隔离问题, 设计了一种薄膜底面Helmholtz腔声学超材料, 该超材料由薄膜底面Helmholtz腔附加质量单元构成. 使用有限元法, 计算了超材料在20—1200 Hz频段内的传输损失曲线与各阶共振频率, 并在实验中验证了数值计算的真实性. 研究结果表明, 超材料在20—1200 Hz频段内隔声性能良好, 出现了6个隔声峰, 其中100 Hz以下的2个隔声峰传输损失分别高达44.29 dB与67.43 dB, 整个频段内的最高传递损失为90.18 dB. 相较于单一的Helmholtz腔、薄膜声学超材料或传统材料, 本超材料的隔声性能有了较大提升. 结合共振频率与隔声峰处的振动模式图, 进一步分析了超材料的隔声机理. 计算了超材料的透射系数与反射系数, 使用等效参数提取法, 得到了超材料的等效模量与等效密度, 在隔声峰处发现了负等效密度, 同时发现其等效模量接近于零, 并由能量角度进一步分析了异常等效参数的产生机理. 通过等效电路法, 得到了超材料的声阻抗, 较精确地计算了超材料的首阶共振频率, 并分析了产生误差的原因. 研究了附加偏心质量单元对超材料隔声性能的影响, 发现附加偏心质量单元可以抑制反对称共振模态的出现, 同时大大增加了超材料的隔声峰数量, 在实验中这一说法得以验证.
-
关键词:
- Helmholtz腔 /
- 薄膜声学超材料 /
- 有限元法 /
- 隔声性能 /
- 负参数
Aiming at the isolation of low-frequency noise, an acoustic metamaterial is designed based on Helmholtz cavity and thin film structure. It consists of a Helmholtz cavity with film bottom and the mass block attached to the cavity. By the finite element method, the transmission losses and resonance frequencies of metamaterials in a frequency range of 20－1200 Hz are calculated and also verified experimentally. The results show that the metamaterial has great sound insulation performance in the frequency range. There are six sound insulation peaks, of which the two sound insulation peaks below 100 Hz have the transmission losses of 44.29 dB and 67.43 dB, respectively. The maximum transmission loss in the whole frequency range is 90.18 dB. Comparing with the normal Helmholtz cavity or thin film acoustic metamaterial or traditional material, the sound insulation performance of the metamaterial is improved greatly. By analyzing the resonance and vibration mode diagram at the sound insulation peaks comprehensively, the sound insulation mechanism of the metamaterial is further explored. The results show that many resonance modes have no effect on transmission loss only when the resonance mode can be coupled with the incident wave and is not an antisymmetric mode which can affect the transmission loss. The transmission and reflection coefficient of the metamaterial are calculated by the finite element method, and through the method for retrieving effective properties, the effective mass density and effective modulus are obtained. It is found that there is a negative effective mass density at the sound insulation peak, meanwhile the effective modulus is close to zero. The generation mechanism of abnormal equivalent parameters is analyzed from the energy view point. The acoustic impedance of the metamaterial is obtained by an equivalent circuit method, through which the first resonance frequency is calculated relatively accurately. According to the results of the previous study on sound insulation mechanism, the effect of the eccentric mass unit on the sound insulation performance of metamaterial is studied. It is found that the eccentric mass can greatly reduce the antisymmetric resonance mode and increase the sound insulation peak of the structure, which is also verified experimentally. The results provide a reference for designing the acoustic metamaterials.-
Keywords:
- Helmholtz cavity /
- thin film acoustic metamaterials /
- finite element method /
- sound insulation performance /
- negative parameter
[1] William B A, Lisa M M, Kelsey B, Stephen B, John L A 2019 Environ. Sci. Technol. 53 7126
Google Scholar
[2] 周榕 2017 硕士学位论文 (南京: 江苏大学)
Zhou Y 2017 M. S. Thesis (Nanjing: Jiangsu University) (in Chinese)
[3] Wu J H, Ma F Y, Zhang S W, Shen L 2006 J. Mech. Eng. 52 68
[4] 丁昌林, 董仪宝, 赵晓鹏 2018 67 194301
Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301
[5] Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K 2010 Phys. Rev. Lett. 104 054301
Google Scholar
[6] 沈惠杰, 郁殿龙, 汤智胤, 苏永生, 李雁飞, 刘江伟 2019 68 144301
Shen H J, Yu D L, Tang Z Y, Su Y S, Li Y F, Liu J W 2019 Acta Phys. Sin. 68 144301
[7] Chen H J, Zhai S L, Ding C L, Liu S, Luo C R, Zhao X P 2015 J. Appl. Phys. 118 094901
Google Scholar
[8] Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756
Google Scholar
[9] Nemat-Nasser S, Willis J R, Srivastava A, Amirkhizi A V 2011 Phys. Rev. B 83 104103
Google Scholar
[10] 丁昌林, 赵晓鹏 2009 58 6351
Google Scholar
Ding C L, Zhao X P 2009 Acta Phys. Sin. 58 6351
Google Scholar
[11] Liu Z, Zhang X X, Chan C T, Sheng P 2000 Science 289 1734
Google Scholar
[12] 贺子厚, 赵静波, 姚宏, 蒋娟娜, 张帅, 陈鑫 2018 硅酸盐学报 47 983
He Z H, Zhao J B, Yao H, Jiang J N, Zhang S Chen X 2018 J. Chin. Ceramic Soc. 47 983
[13] 高南沙, 侯宏 2018 材料导报 32 322
Google Scholar
Gao N S, Hou H 2018 Mater. Rev. 32 322
Google Scholar
[14] 王莎, 林书玉 2019 68 024303
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
[15] 刘娇, 侯志林, 傅秀军 2015 64 154302
Liu J, Hou Z L, Fu X J 2015 Acta Phys. Sin. 64 154302
[16] Cheng Y, Xu J Y, Liu X J 2008 Appl. Phys. Lett. 92 051913
Google Scholar
[17] 贾晓珍 2018 硕士学位论文 (西安: 陕西师范大学)
Jia X Z 2018 M. S. Thesis (Xi′an: Shaanxi Normal Univer-sity) (in Chinese)
[18] Chen Y, Huang G, Zhou X, Hu G, Sun C 2014 J. Acoust. Soc. Am. 136 969
Google Scholar
[19] Fang N, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nature Mater. 5 452
Google Scholar
[20] 姜久龙, 姚宏, 杜军, 赵静波, 邓涛 2017 66 064301
Jiang J L, Yao H, Du J, Zhao J B, Deng T 2017 Acta Phys. Sin. 66 064301
[21] Naify C J, Chang C M, Mcknight G, Nutt S 2011 J. Appl. Phys. 110 751
[22] 梅军, 马冠聪, 杨旻, 杨志宇, 温维佳, 沈平 2012 物理 41 425
Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Shen P 2012 Physics 41 425
[23] Cheng Y, Zhou C, Yuan B G, Wu D J, Wei Q, Liu X J 2015 Nature Mater. 14 1013
Google Scholar
[24] 周榕, 吴卫国, 闻轶凡 2017 声学技术 36 297
Zhou Y, Wu W G, Wen Y F 2017 Tech. Acoust. 36 297
[25] Abbad A 2016 SAE International 9th International Styrian Noise, Vibration & Harshness Congress Warrendale, United States, June 22, 2016 p2011
[26] Long H, Cheng Y, Liu X 2018 Sci. Rep. 8 15678
Google Scholar
[27] 陈鑫, 姚宏, 赵静波, 张帅, 贺子厚, 蒋娟娜 2019 68 084302
Chen X, Yao H, Zhao J B, Zhang S, He Z H, Jiang J N 2019 Acta Phys. Sin. 68 084302
[28] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (南京: 南京大学出版社) 第84页
Du G H, Zhu Z M, Gong X F 2012 Acoustic Basis (Nanjing: Nanjing University Press) p84
[29] Fokin V, Ambati M, Sun C, Zhang X 2007 Phys. Rev. B 76 144302
Google Scholar
[30] 贺子厚, 赵静波, 姚宏, 张帅, 蒋娟娜, 陈鑫 2019 68 134302
Google Scholar
He Z H, Zhao J B, Yao H, Zhang S, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302
Google Scholar
-
图 1 材料结构 (a)结构示意图; (b)结构参数
Fig. 1. Material structure: (a) Structural sketch; (b) structure parameter.
图 4 共振模态(颜色条表示位移的取值, 单位为mm, 其余图同) (a) 69.44 Hz; (b) 325.40 Hz
Fig. 4. Resonance mode (color bar represents the displacement values, unit: mm): (a) 69.44 Hz; (b) 325.40 Hz.
图 5 共振模态 (a) 25.05 Hz; (b) 68.53 Hz; (c) 420.72 Hz; (d) 622.76 Hz; (e) 944.71 Hz; (f) 1075.80 Hz
Fig. 5. Resonance mode: (a) 25.05 Hz; (b) 68.53 Hz; (c) 420.72 Hz; (d) 622.76 Hz; (e) 944.71 Hz; (f) 1075.80 Hz.
图 6 隔声峰处振动模式图 (a) 25.10 Hz; (b) 67.43 Hz; (c) 415.49 Hz; (d) 626.30 Hz; (e) 952.81 Hz; (f) 1080.08 Hz
Fig. 6. Vibration mode diagrams at sound insulation peak: (a) 25.10 Hz; (b) 67.43 Hz; (c) 415.49 Hz; (d) 626.30 Hz; (e) 952.81 Hz; (f) 1080.08 Hz.
图 7 Helmholtz腔(a)及其等价电路模型(b)
Fig. 7. Helmholtz cavity (a) and its equivalent circuit model
图 8 薄膜底面Helmholtz腔(a)及其等价电路模型(b)
Fig. 8. Helmholtz cavity with thin film bottom (a) and its equivalent circuit model.
图 10 实验示意图 (a), (b)样件实物图; (c)实验装置
Fig. 10. Experimental schematic diagrams: (a), (b) Sample structure; (c) experimental facility.
图 11 实验测得的传输损失曲线与数值计算结果的对比
Fig. 11. Comparison between experimentally measured transmission loss curve and the results obtained by the finite element method.
图 12 (a)透射系数; (b)反射系数
Fig. 12. (a) Transmission coefficient; (b) reflection coefficient.
图 13 等效参数 (a)等效密度; (b)等效模量
Fig. 13. Effective parameters: (a) Effective mass density; (b) effective modulus.
图 15 (a)偏心质量单元与中心质量单元的传输损失曲线; (b)当 l 值不同时, 超材料的传输损失曲线
Fig. 15. (a) Comparison of transmission loss between eccentric mass unit and central mass unit; (b) transmission loss curves when l is different.
图 16 振动模式图 (a) 28.03 Hz; (b) 61.27 Hz; (c) 71.29 Hz; (d) 328.22 Hz; (e) 396.30 Hz; (f) 466.81 Hz
Fig. 16. Vibration mode: (a) 28.03 Hz; (b) 61.27 Hz; (c) 71.29 Hz; (d) 328.22 Hz; (e) 396.30 Hz; (f) 466.81 Hz.
图 17 中心质量单元设计时, 68.83 Hz共振频率所对应共振模态图
Fig. 17. Resonance modal diagram with the resonance frequency of 68.83 Hz when the mass unit is at the center.
图 18 实验验证 (a)样件图; (b)传输损失曲线
Fig. 18. Experimental verification: (a) Sample structure; (b) transmission loss curves.
表 1 材料参数
Table 1. Material parameters.
Material ρ/kg·m–3 E/1010 Pa Possion rate Tungsten 19100 35.41 0.35 Silastic 1300 1.175 × 10–5 0.469 Steel 7780 21.06 0.3 
下载: 导出CSV
-
[1] William B A, Lisa M M, Kelsey B, Stephen B, John L A 2019 Environ. Sci. Technol. 53 7126
Google Scholar
[2] 周榕 2017 硕士学位论文 (南京: 江苏大学)
Zhou Y 2017 M. S. Thesis (Nanjing: Jiangsu University) (in Chinese)
[3] Wu J H, Ma F Y, Zhang S W, Shen L 2006 J. Mech. Eng. 52 68
[4] 丁昌林, 董仪宝, 赵晓鹏 2018 67 194301
Ding C L, Dong Y B, Zhao X P 2018 Acta Phys. Sin. 67 194301
[5] Lee S H, Park C M, Seo Y M, Wang Z G, Kim C K 2010 Phys. Rev. Lett. 104 054301
Google Scholar
[6] 沈惠杰, 郁殿龙, 汤智胤, 苏永生, 李雁飞, 刘江伟 2019 68 144301
Shen H J, Yu D L, Tang Z Y, Su Y S, Li Y F, Liu J W 2019 Acta Phys. Sin. 68 144301
[7] Chen H J, Zhai S L, Ding C L, Liu S, Luo C R, Zhao X P 2015 J. Appl. Phys. 118 094901
Google Scholar
[8] Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Sheng P 2012 Nat. Commun. 3 756
Google Scholar
[9] Nemat-Nasser S, Willis J R, Srivastava A, Amirkhizi A V 2011 Phys. Rev. B 83 104103
Google Scholar
[10] 丁昌林, 赵晓鹏 2009 58 6351
Google Scholar
Ding C L, Zhao X P 2009 Acta Phys. Sin. 58 6351
Google Scholar
[11] Liu Z, Zhang X X, Chan C T, Sheng P 2000 Science 289 1734
Google Scholar
[12] 贺子厚, 赵静波, 姚宏, 蒋娟娜, 张帅, 陈鑫 2018 硅酸盐学报 47 983
He Z H, Zhao J B, Yao H, Jiang J N, Zhang S Chen X 2018 J. Chin. Ceramic Soc. 47 983
[13] 高南沙, 侯宏 2018 材料导报 32 322
Google Scholar
Gao N S, Hou H 2018 Mater. Rev. 32 322
Google Scholar
[14] 王莎, 林书玉 2019 68 024303
Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
[15] 刘娇, 侯志林, 傅秀军 2015 64 154302
Liu J, Hou Z L, Fu X J 2015 Acta Phys. Sin. 64 154302
[16] Cheng Y, Xu J Y, Liu X J 2008 Appl. Phys. Lett. 92 051913
Google Scholar
[17] 贾晓珍 2018 硕士学位论文 (西安: 陕西师范大学)
Jia X Z 2018 M. S. Thesis (Xi′an: Shaanxi Normal Univer-sity) (in Chinese)
[18] Chen Y, Huang G, Zhou X, Hu G, Sun C 2014 J. Acoust. Soc. Am. 136 969
Google Scholar
[19] Fang N, Xi D J, Xu J Y, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nature Mater. 5 452
Google Scholar
[20] 姜久龙, 姚宏, 杜军, 赵静波, 邓涛 2017 66 064301
Jiang J L, Yao H, Du J, Zhao J B, Deng T 2017 Acta Phys. Sin. 66 064301
[21] Naify C J, Chang C M, Mcknight G, Nutt S 2011 J. Appl. Phys. 110 751
[22] 梅军, 马冠聪, 杨旻, 杨志宇, 温维佳, 沈平 2012 物理 41 425
Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Shen P 2012 Physics 41 425
[23] Cheng Y, Zhou C, Yuan B G, Wu D J, Wei Q, Liu X J 2015 Nature Mater. 14 1013
Google Scholar
[24] 周榕, 吴卫国, 闻轶凡 2017 声学技术 36 297
Zhou Y, Wu W G, Wen Y F 2017 Tech. Acoust. 36 297
[25] Abbad A 2016 SAE International 9th International Styrian Noise, Vibration & Harshness Congress Warrendale, United States, June 22, 2016 p2011
[26] Long H, Cheng Y, Liu X 2018 Sci. Rep. 8 15678
Google Scholar
[27] 陈鑫, 姚宏, 赵静波, 张帅, 贺子厚, 蒋娟娜 2019 68 084302
Chen X, Yao H, Zhao J B, Zhang S, He Z H, Jiang J N 2019 Acta Phys. Sin. 68 084302
[28] 杜功焕, 朱哲民, 龚秀芬 2012 声学基础 (南京: 南京大学出版社) 第84页
Du G H, Zhu Z M, Gong X F 2012 Acoustic Basis (Nanjing: Nanjing University Press) p84
[29] Fokin V, Ambati M, Sun C, Zhang X 2007 Phys. Rev. B 76 144302
Google Scholar
[30] 贺子厚, 赵静波, 姚宏, 张帅, 蒋娟娜, 陈鑫 2019 68 134302
Google Scholar
He Z H, Zhao J B, Yao H, Zhang S, Jiang J N, Chen X 2019 Acta Phys. Sin. 68 134302
Google Scholar
下载:
计量
- 文章访问数: 11378
- PDF下载量: 254
- 被引次数: 0
