-
本文采用粒子模拟方法, 针对长脉冲激光在非均匀等离子体中的传输过程, 特别是在1/4临界密度附近, 等离子体中受激散射的非线性演化现象, 进行了细致的模拟研究. 研究结果表明: 在1/4临界面附近所产生的受激拉曼散射不稳定性, 其散射光在等离子体中被捕获, 并在该区域形成电磁孤子. 电磁孤子的振幅随着不稳定性的发展而提高, 并由此而产生一个有质动力场驱动周围的电子运动, 离子随后被电荷分离场加速, 最终形成准中性的密度坑. 在单个密度坑形成后, 由于该密度坑周围等离子体密度和温度产生了变化, 使得等离子体中逐渐形成更多的密度坑. 这些密度坑将等离子体分割成不连续的密度分布, 而这种密度分布最终明显地抑制了受激拉曼散射和受激布里渊散射不稳定性的发展.Based on particle-in-cell simulations, the propagation of intense long pulse lasers in non-uniform plasma, and particularly, the formation of plasma density cavities caused by the nonlinear evolution of stimulated Raman scattering (SRS) near the quarter critical density, and its effects on parametric instabilities have been studied. It is found that the stimulated Raman scattering instability developed near the quarter critical density leads to the trapping of scattered light and subsequent formation of a local electromagnetic solitary wave. Its amplitude increases with the development of the SRS instability, which pushes surrounding electrons and ions to form a quasi-neutral density cavity. When the first density cavity is formed, the plasma density evolves in such a way that more density cavities are formed during the laser interaction and subsequently the plasma is split into a few discontinuous portions. This new density profile finally tends to suppress the development of both SRS and the stimulated Brillouin scattering (SBS) instabilities considerably.
-
Keywords:
- stimulated Raman scattering /
- electromagnetic soliton /
- laser transmission /
- particle-in-cell simulation
[1] Kruer W 1988 The Physics of Laser Plasma Interactions (New York: Addison-Wesley) p74
[2] Kaw P K 2017 Rev. Mod. Plasma Phys. 1 2
Google Scholar
[3] Cheung P Y, Wong A Y, Darrow C B, Qian S Z 1982 Phys. Rev. Lett. 48 1348
Google Scholar
[4] Borghesi M, Bulanov S, Campbell D H, Clarke R J, Esirkepov T Zh, Galimberti M, Gizzi L A, MacKinnon A J, Naumova N M, Pegoraro F, Ruhl H, Schiavi A, Willi O 2002 Phys. Rev. Lett. 88 135002
Google Scholar
[5] Langdon A B, Lasinski B F 1983 Phys. Fluids 26 582
Google Scholar
[6] Weber S, Riconda C, Tikhonchuk V 2005 Phys. Rev. Lett. 94 055005
Google Scholar
[7] Klimo O, Weber S, Tikhonchuk V T, Limpouch J 2010 Plasma Phys. Control. Fusion 52 055013
Google Scholar
[8] Zhao Y, Sheng Z M, Weng S M, Ji S Z, Zhu J Q 2019 High Power Laser Sci. Eng. 7 e20
Google Scholar
[9] Klimo O, Tikhonchuk V T 2013 Plasma Phys. Control. Fusion 55 095002
Google Scholar
[10] Eliasson B 2013 Mod. Phys. Lett. B 27 1330005
[11] Esirkepov T, Nishihara K, Bulanov S V, Pegoraro F 2002 Phys. Rev. Lett. 89 275002
Google Scholar
[12] 盛政明, 张杰, 余玮 2003 52 125
Google Scholar
Sheng Z M, Zhang J, Yu W 2003 Acta Phys. Sin. 52 125
Google Scholar
[13] Sheng Z M, Zhang J, Umstadter D 2003 Appl. Phys. B 77 673
[14] Yu L L, Sheng Z M, Zhang J 2009 J. Opt. Soc. Am. B 26 2095
Google Scholar
[15] Xiao C Z, Liu Z J, Wu D, Zheng C Y, He X T 2015 Phys. Plasmas 22 052121
Google Scholar
[16] Craxton R S, Anderson K S, Boehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty P W, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[17] Kaw P K, Kruer W L, Liu C S, Nishikawa K 1976 Advances in Plasma Physics (Vol. 6) (New York: John Wiley and Sons, Inc.)
[18] Liu C S, Tripathi V K, Eliasson B 2019 High-Power Laser-Plasma Interaction (Cambridge: Cambridge University Press)
[19] Pesme D, Laval G, Pellat R 1973 Phys. Rev. Lett. 31 203
Google Scholar
[20] Wang Y X, Wang Q, Zheng C Y, Liu Z J, Liu C S, He X T 2018 Phys. Plasmas 25 100702
Google Scholar
[21] Rosenbluth M N 1972 Phys. Rev. Lett. 29 565
Google Scholar
[22] Liu C S, Rosenbluth M N, White R B 1974 Phys. Fluids 17 1211
Google Scholar
[23] Zakharov V E 1972 Sov. Phys. JETP 35 908
[24] Zhao Y, Yu L L, Weng S M, Ren C, Liu C S, Sheng Z M 2017 Phys. Plasmas 24 092116
Google Scholar
[25] Brady C 2014 Users Manual for the EPOCH PIC Codes (Coventry: University of Warwick) pp12－50
[26] Naumova N M, Bulanov S V, Esirkepov T Zh, Farina D, Nishihara K, Pegoraro F, Ruhl H, Sakharov A S 2001 Phys. Rev. Lett. 87 185004
Google Scholar
[27] Esirkepov T Zh, Kamenets F F 1999 JETP Lett. 68 36
[28] White R, Kaw P, Pesme D, Rosenbluth M N, Laval G, Huff R, Varma R 1974 Nucl. Fusion 14 45
Google Scholar
[29] Zhao Y, Zheng J, Chen M, Yu L L, Weng S M, Ren C, Liu C S, Sheng Z M 2014 Phys. Plasmas 21 112114
Google Scholar
[30] DuBois D F, Forslund D W 1974 Phys. Rev. Lett. 33 1013
Google Scholar
[31] Sheng Z M, Nishihara K, Honda T, Sentoku Y, Mima K, Bulanov S V 2001 Phys. Rev. E 64 066409
Google Scholar
-
图 1 (a)随时间变化的离子密度分布; (b) 2100T0时刻的离子密度分布
Fig. 1. (a) Temporal and spatial variation of ion density distribution; (b) the ion density distribution at 2100T0. The red dotted line marks the density cavity with the width of 2λ0.
图 2 (a)归一化电场Ey的时空演化图, 其中的归一化量纲El为入射激光的电场强度; (b) 0−2000T0, 200−400 μm等离子体中的电场Ey在k – ω空间中的分布; (c) 2000T0−4000T0, 200−400 μm等离子体中的电场Ey在k – ω空间中的分布
Fig. 2. (a) Spatio-temporal evolution of the electric field Ey, Ey is normalized to El, which is the electric field intensity of incident laser; (b) distribution of electric field in (k, ω) space corresponding to the time window [0−2000]T0 and the space window [200−400] μm; (c) distribution of electric field in (k, ω) space corresponding to the time window [2000−4000]T0 and the space window [200−400] μm.
图 3 (a)在不同的初始电子温度下, 1/4临界密度处等离子体密度坑的产生时间对比; (b)在不同的初始离子温度下, 1/4临界密度处等离子体密度坑的产生时间对比
Fig. 3. (a) Comparison of the generation time of plasma density cavity with different initial electron temperatures at quarter critical density; (b) comparison of the generation time of plasma density cavity with different initial ion temperatures at quarter critical density.
图 4 (a)随时空变化的离子密度分布; (b)密度坑产生后, 在3200T0时刻, 密度坑附近的离子被加速到较高的能量
Fig. 4. (a) Temporal and spatial variation of ion density distribution; (b) after the formation of density cavities, the ions near the density cavities have been accelerated to a higher energy at the moment of 3200T0.
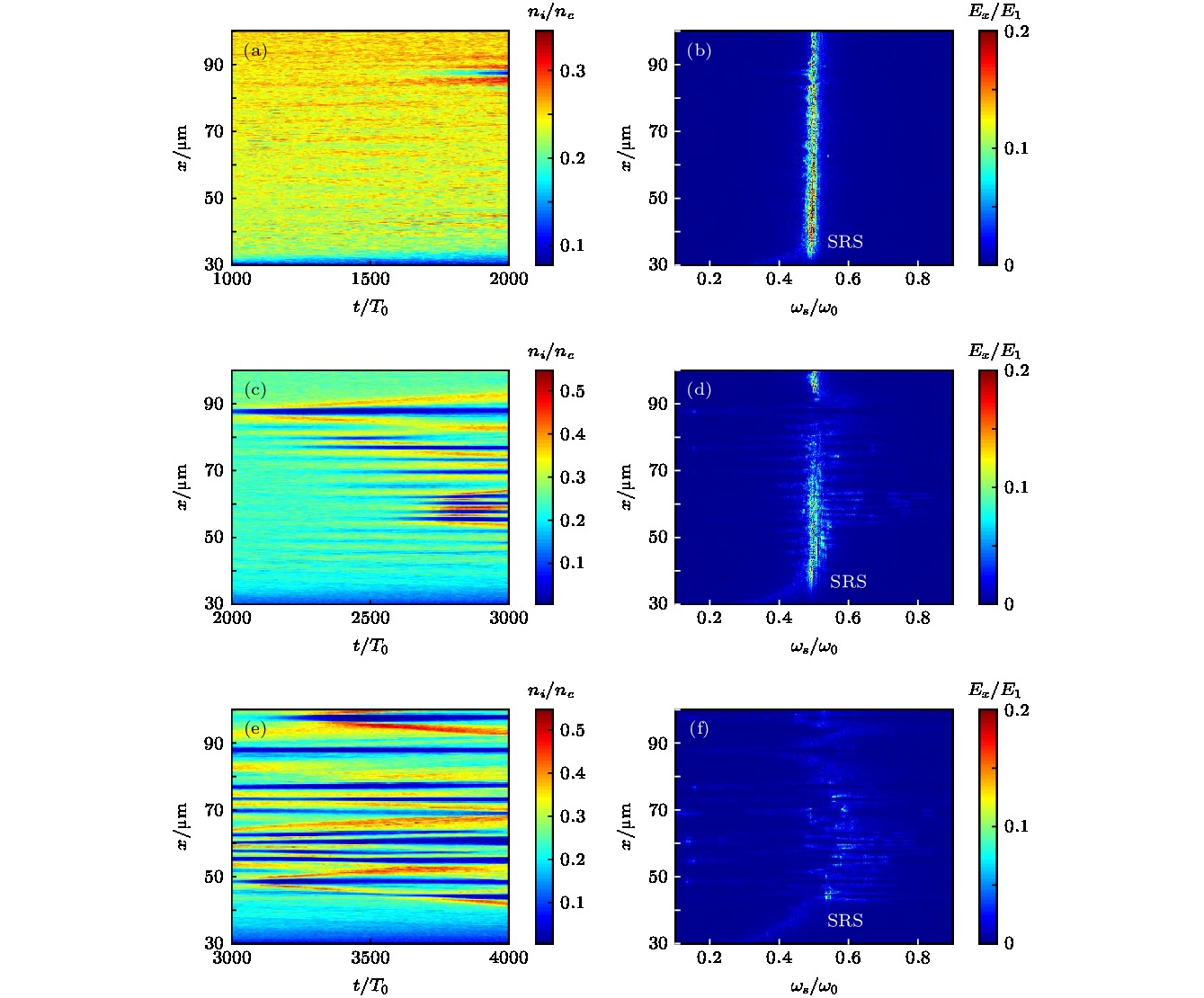
图 5 (a), (c), (e)不同时间段中的离子密度在x – t空间中的分布; (b), (d), (f)不同时间段中的纵向电场Ex在x – ω空间中的分布; 这些离子密度以及纵向电场的分布, 分别反映了不稳定区域或激光等离子体不稳定性的发展情况
Fig. 5. (a), (c), (e) Temporal and spatial variation of ion density distribution in different time windows; (b), (d), (f) the longitudinal field Ex in (x, ω) space. The ion and Ex distribution represent the development of instability regions and parametric instability, respectively.
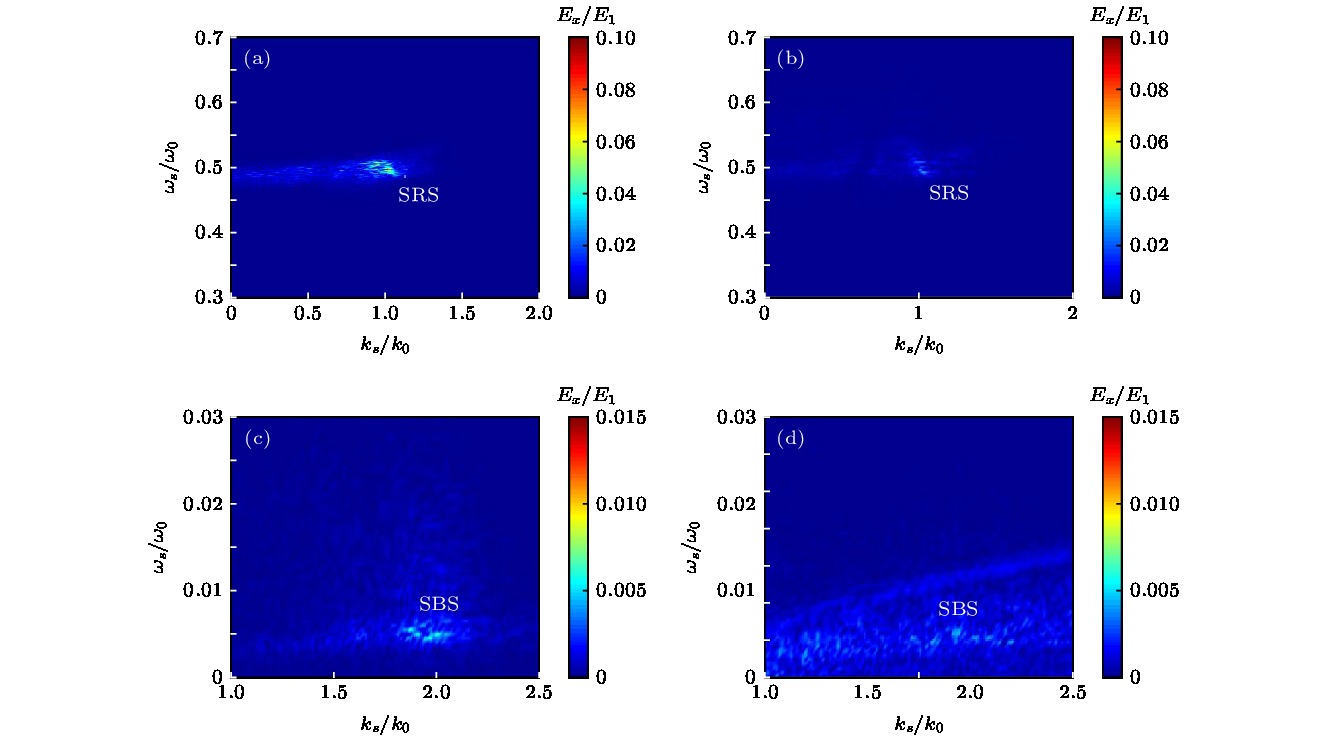
图 6 (a), (c) 0−2000T0纵场Ex在k-ω空间的分布; (b), (d) 2000T0−4000T0纵场Ex在k – ω空间的分布, 相应频率与波矢的纵场Ex, 分别对应了SBS和SRS不稳定性的发展
Fig. 6. (a), (c) The Ex distribution in (k, ω) space corresponding to the time window [0−2000]T0; (b), (d) the Ex distribution in (k, ω) space corresponding to the time window [2000T0−4000]T0. The longitudinal field Ex represents the development of SRS and SBS instabilities in the different time windows, respectively.
图 7 (a)左行波在频率空间中随时间的变化; (b) SRS的份额随时间的变化; (c) SBS的份额随时间的变化
Fig. 7. (a) The temporal evolution of left traveling wave in frequency space; (b) the temporal evolution of SRS; (c) the temporal evolution of SBS.
-
[1] Kruer W 1988 The Physics of Laser Plasma Interactions (New York: Addison-Wesley) p74
[2] Kaw P K 2017 Rev. Mod. Plasma Phys. 1 2
Google Scholar
[3] Cheung P Y, Wong A Y, Darrow C B, Qian S Z 1982 Phys. Rev. Lett. 48 1348
Google Scholar
[4] Borghesi M, Bulanov S, Campbell D H, Clarke R J, Esirkepov T Zh, Galimberti M, Gizzi L A, MacKinnon A J, Naumova N M, Pegoraro F, Ruhl H, Schiavi A, Willi O 2002 Phys. Rev. Lett. 88 135002
Google Scholar
[5] Langdon A B, Lasinski B F 1983 Phys. Fluids 26 582
Google Scholar
[6] Weber S, Riconda C, Tikhonchuk V 2005 Phys. Rev. Lett. 94 055005
Google Scholar
[7] Klimo O, Weber S, Tikhonchuk V T, Limpouch J 2010 Plasma Phys. Control. Fusion 52 055013
Google Scholar
[8] Zhao Y, Sheng Z M, Weng S M, Ji S Z, Zhu J Q 2019 High Power Laser Sci. Eng. 7 e20
Google Scholar
[9] Klimo O, Tikhonchuk V T 2013 Plasma Phys. Control. Fusion 55 095002
Google Scholar
[10] Eliasson B 2013 Mod. Phys. Lett. B 27 1330005
[11] Esirkepov T, Nishihara K, Bulanov S V, Pegoraro F 2002 Phys. Rev. Lett. 89 275002
Google Scholar
[12] 盛政明, 张杰, 余玮 2003 52 125
Google Scholar
Sheng Z M, Zhang J, Yu W 2003 Acta Phys. Sin. 52 125
Google Scholar
[13] Sheng Z M, Zhang J, Umstadter D 2003 Appl. Phys. B 77 673
[14] Yu L L, Sheng Z M, Zhang J 2009 J. Opt. Soc. Am. B 26 2095
Google Scholar
[15] Xiao C Z, Liu Z J, Wu D, Zheng C Y, He X T 2015 Phys. Plasmas 22 052121
Google Scholar
[16] Craxton R S, Anderson K S, Boehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty P W, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[17] Kaw P K, Kruer W L, Liu C S, Nishikawa K 1976 Advances in Plasma Physics (Vol. 6) (New York: John Wiley and Sons, Inc.)
[18] Liu C S, Tripathi V K, Eliasson B 2019 High-Power Laser-Plasma Interaction (Cambridge: Cambridge University Press)
[19] Pesme D, Laval G, Pellat R 1973 Phys. Rev. Lett. 31 203
Google Scholar
[20] Wang Y X, Wang Q, Zheng C Y, Liu Z J, Liu C S, He X T 2018 Phys. Plasmas 25 100702
Google Scholar
[21] Rosenbluth M N 1972 Phys. Rev. Lett. 29 565
Google Scholar
[22] Liu C S, Rosenbluth M N, White R B 1974 Phys. Fluids 17 1211
Google Scholar
[23] Zakharov V E 1972 Sov. Phys. JETP 35 908
[24] Zhao Y, Yu L L, Weng S M, Ren C, Liu C S, Sheng Z M 2017 Phys. Plasmas 24 092116
Google Scholar
[25] Brady C 2014 Users Manual for the EPOCH PIC Codes (Coventry: University of Warwick) pp12－50
[26] Naumova N M, Bulanov S V, Esirkepov T Zh, Farina D, Nishihara K, Pegoraro F, Ruhl H, Sakharov A S 2001 Phys. Rev. Lett. 87 185004
Google Scholar
[27] Esirkepov T Zh, Kamenets F F 1999 JETP Lett. 68 36
[28] White R, Kaw P, Pesme D, Rosenbluth M N, Laval G, Huff R, Varma R 1974 Nucl. Fusion 14 45
Google Scholar
[29] Zhao Y, Zheng J, Chen M, Yu L L, Weng S M, Ren C, Liu C S, Sheng Z M 2014 Phys. Plasmas 21 112114
Google Scholar
[30] DuBois D F, Forslund D W 1974 Phys. Rev. Lett. 33 1013
Google Scholar
[31] Sheng Z M, Nishihara K, Honda T, Sentoku Y, Mima K, Bulanov S V 2001 Phys. Rev. E 64 066409
Google Scholar
下载:
计量
- 文章访问数: 9345
- PDF下载量: 79
- 被引次数: 0
