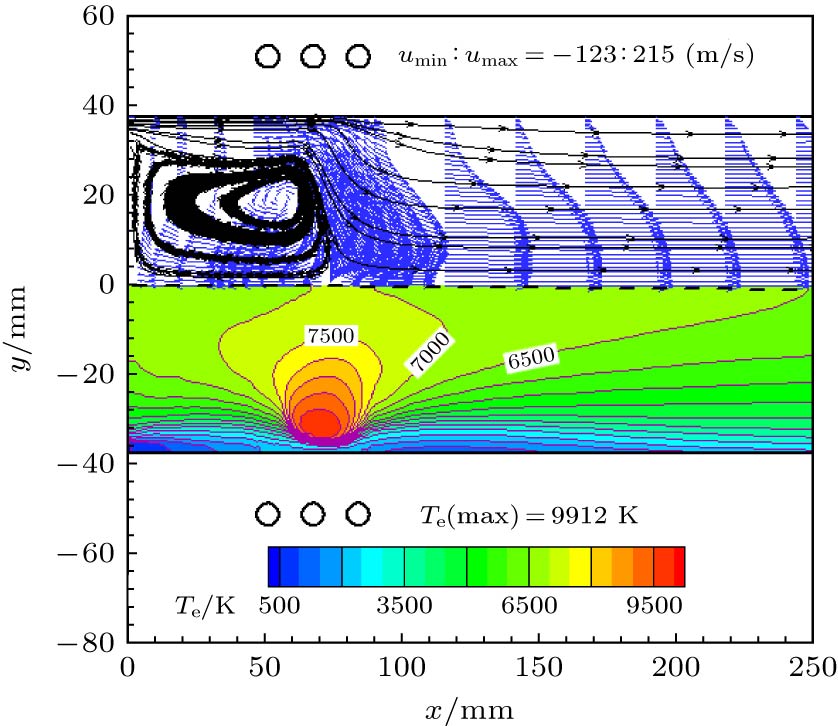
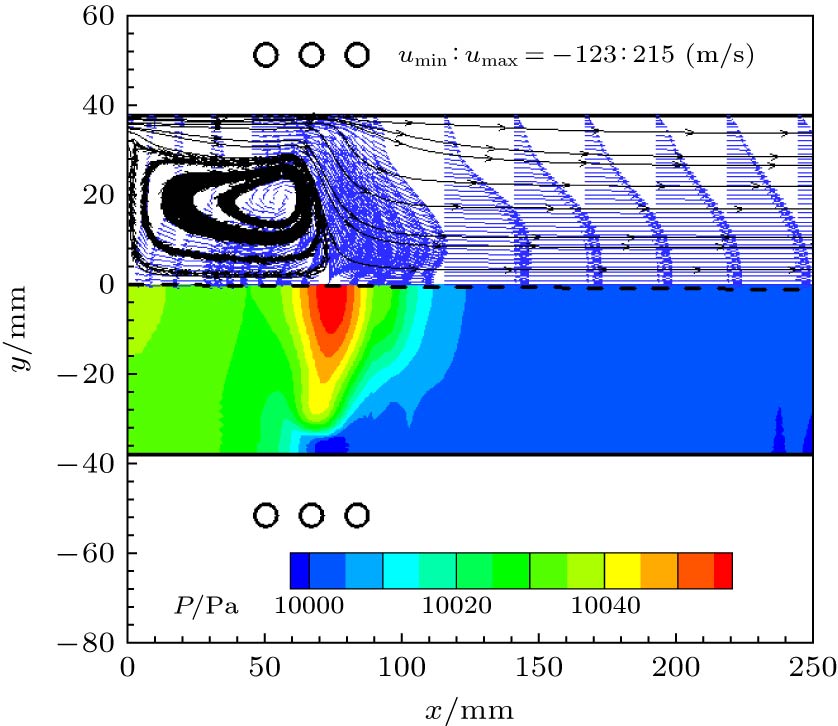
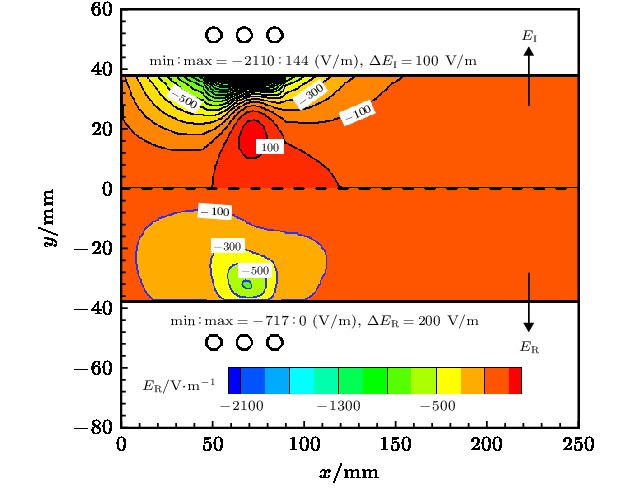
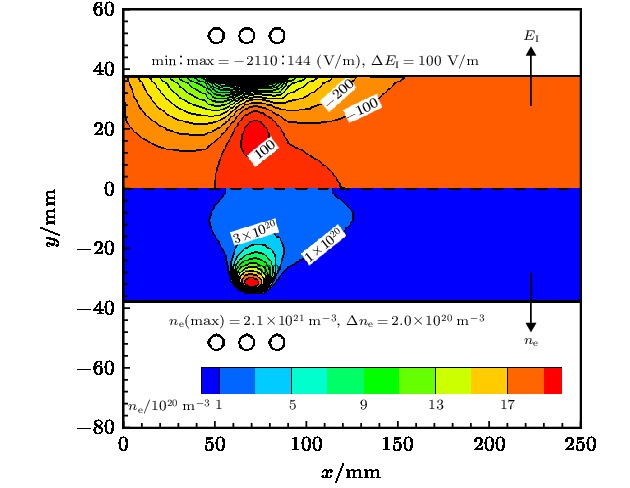
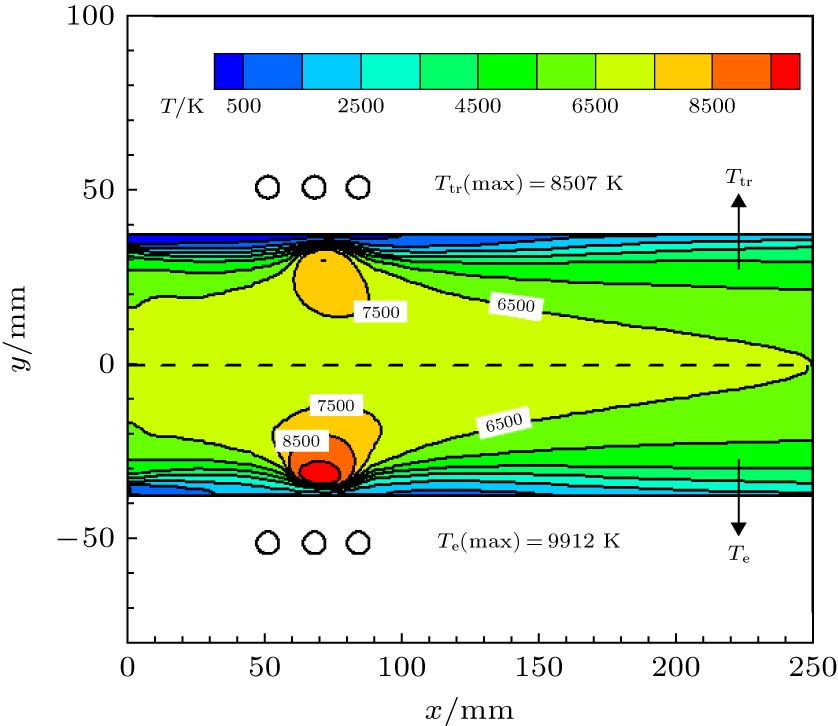
-
以航天领域中研究再入飞行器热防护系统的感应耦合等离子体(inductively coupled plasma, ICP)风洞为研究对象, 通过流场-电磁场-化学场-热力场-湍流场多场耦合求解研究ICP风洞流场与电磁场的分布特性及其相互作用机理. 数值模拟中, 基于热化学非平衡等离子体磁流体动力学模型准确模拟了空气ICP的高频放电、焦耳加热、能量转化、粒子内能交换等过程, 通过多物理场耦合计算模拟得到了100 kW级ICP风洞内空气等离子体的电子温度、粒子数密度、洛伦兹力、焦耳加热率、速度、压强、电场强度的分布规律. 研究结果表明: 在感应线圈区靠近等离子体炬壁附近, 等离子体流动处于热力学非平衡状态; 洛伦兹力对感应线圈区空气粒子的动量传递和电子热运动起着控制作用.In this paper, the inductively coupled plasma (ICP) wind tunnel, which is widely used in the development of thermal protection system for reentry vehicle in the aerospace field, is studied. The distribution properties and the interaction mechanism of the flow field and electromagnetic field are investigated by numerically solving the multi-physics fields coupling among the flow field, electromagnetic field, thermodynamic field and turbulent field. In the numerical simulation, the thermochemical non-equilibrium plasma magneto-hydrodynamic model is used to accurately simulate the high-frequency discharge, Joule heating, energy conversion, and internal energy exchange of air ICP. Finally, the distribution of electron temperature, particle number density, Lorentz force, Joule heating rate, velocity, pressure and electric field strength of air plasma are obtained through the multi-physics field coupling calculation. The results show that the plasma flow is in a thermodynamic non-equilibrium state near the torch wall in the induction coil region and that the Lorentz force plays an important role in controlling the momentum transfer. A strong eddy flow occurs between the inlet and the second turn of the inductive coil. The eddy flow has a close relationship with the negative pressure gradient and the electromagnetic heating phenomenon in the induction coil region. The radial Lorentz force is always negative. This indicates that the free electrons are generated near the wall due to the fact that the skin effect are always subjected to a force making them move to the central axis of the ICP torch. The maximum value of the radial Lorentz force is 3.95 times higher than that of the axial Lorentz. This indicates that the momentum transfer is predominantly radial. The Joule heating effect of the air particles is also affected by the radial Lorentz force. The maximum value of EI is 2.9 times larger than the real part of electric field, ER. The positive EI is generated by the free electrons inside the plasma. The number density of free electrons reaches a maximum value at a distance of 5.5 mm far from the inner wall surface of the torch below the second induction coil. 91% of N2 are dissociated into atomic N near the central axis. The maximum electron and translational temperature simulated in this paper are 9921 K and 8507 K, respectively.
-
Keywords:
- inductively coupled plasma /
- electromagnetic and flow fields /
- nonequilibrium /
- numerical simulation
[1] Suzuki T, Fujita K, Ando K, Sakai T 2008 J. Thermophys. Heat Tr. 22 382
Google Scholar
[2] Suzuki T, Fujita K, Sakai T 2010 J. Thermophys. Heat Tr. 24 589
Google Scholar
[3] Yamada K, Miyatani S, Maeno H, Abe T 2013 Proceedings of 57th Space Sciences and Technology Conference Tottori, Japan, October 9−11, 2013 p2
[4] 熊举坤, 黄海涛, 2011 化工环保 31 119
Google Scholar
Xiong J K, Huang H T 2011 Environ. Prot. Chem. Indus. 31 119
Google Scholar
[5] 朱海龙, 叶高英, 程昌明, 杨发展, 童洪辉 2014 稀有金属材料与工程 43 2810
Zhu H L, Ye G Y, Cheng C M, Yang F Z, Tong H H 2014 Rare Metal Mat. Eng. 43 2810
[6] Watanabe T, Okumiya H 2004 Sci. Technol. Adv. Mater. 5 639
Google Scholar
[7] Miyatani S, 2014 Proceedings of the 58th Space Science and Technology Union Symposium Nagasaki, Japan, November 11−12, 2014 p2
[8] Reed T B 1961 J. Appl. Phys. 32 821
Google Scholar
[9] Mostaghimi J, Proulx P, Boulos M I 1987 J. Appl. Phys. 61 1753
Google Scholar
[10] Lei F, Li X, Liu Y, Liu D, Yang M, Yu Y 2018 AIP Adv. 8 015003
Google Scholar
[11] Yu M, Takahashi Y, Kihara H, Abe K, Yamada K, Abe T 2014 Plasma Sci. Technol. 16 930
Google Scholar
[12] 魏小龙, 徐浩军, 李建海, 林敏, 宋慧敏 2015 64 175201
Google Scholar
Wei X L, Xu H J, Li J H, Lin M, Song H M 2015 Acta Phys. Sin 64 175201
Google Scholar
[13] Xin Q, Su X, Alavi S, Wang B, Mostaghimi J 2018 Appl. Therm. Eng. 128 785
Google Scholar
[14] Morsli M E, Proulx P, Gravelle D 2011 Plasma Sources Sci. Technol. 20 015016
Google Scholar
[15] Wang Y N, Hou L J, Wang X 2002 Phys. Rev. Lett. 89 155001
Google Scholar
[16] Gao F, Li X, Zhao S, Wang Y 2012 Chin. Phys. B 21 075203
Google Scholar
[17] Yu M, Yamada K, Takahashi Y, Liu K, Zhao T 2016 Phys. Plasmas 23 123523
Google Scholar
[18] 朱海龙, 童洪辉, 杨发展, 程昌明, 叶高英 2013 高电压技术 39 1621
Google Scholar
Zhu H L, Tong H H, Yang F Z, Cheng C M, Ye G Y 2013 High Volt. Eng. 39 1621
Google Scholar
[19] Barnes R M, Nikdel S 1976 J. Appl. Phys. 47 3929
Google Scholar
[20] Mostaghimi J, Boulos M I 1989 Plasma Chem. Plasma Proc. 9 25
Google Scholar
[21] Punjabi S B, Joshi N K, Mangalvedekar H A, Lande B K, Das A K, Kothari D C 2012 Phys. Plasmas 19 012108
Google Scholar
[22] Punjabi S, Barve D, Joshi N, Das A, Kothari D, Ganguli A, Sahasrabhude S, Joshi J 2019 Processes 7 133
Google Scholar
[23] Mostaghimi J, Boulos M I 1990 J. Appl. Phys. 68 2643
Google Scholar
[24] Stewart R A, Vitello P, Graves D B 1994 J. Vac. Sci. Technol. B 12 478
Google Scholar
[25] Munafò A, Alfuhaid S A, Cambier J L, Panesi M 2015 J. Appl. Phys. 118 133303
Google Scholar
[26] Zhang W, Lani A, Panesi M 2016 Phys. Plasmas 23 073512
Google Scholar
[27] Degrez G, Abeele D V, Barbante P, Bottin B 2004 Int. J. Numer. Method H. 14 538
Google Scholar
[28] Sumi T, Fujita K, Kurotaki T, Ito T, Mizuno M, Ishida K 2005 Trans. Japan Soc. Aero. Space Sci. 48 40
Google Scholar
[29] Morsli M E, Proulx P 2007 J. Phys. D: Appl. Phys. 40 4810
Google Scholar
[30] Yu M, Yamada K, Liu K, Zhao T 2019 AIP Adv. 9 015120
Google Scholar
[31] Yu M, Liu K, Zhao T, Zhang Y 2016 J. Korean Phys. Soc. 69 1537
Google Scholar
[32] Yu M, Kihara H, Abe K I, Takahashi Y 2015 J. Korean Phys. Soc. 66 1833
Google Scholar
[33] Dunn M G, Kang S W 1973 Theoretical and Experimental Studies of Reentry Plasmas (Washionton DC: National Aeronautics and Space Administration) pp55−58
[34] Morsli M E, Proulx P 2007 J. Phys. D: Appl. Phys. 40 380
Google Scholar
[35] Park C, Jaffe R L, Partridge H 2001 J. Thermophys. Heat Tr. 15 76
Google Scholar
[36] Lenzner S, Auweter-Kurtz M, Heiermann J, Sleziona P 2000 J. Thermophys. Heat Tr. 14 388
Google Scholar
[37] Fujita K, Mizuno M, Ishida K, Ito T 2008 J. Thermophys. Heat Tr. 22 685
Google Scholar
[38] Yos J M 1963 Transport Properties of Nitrogen, Hydrogen, Oxygen, and Air to 30000 K (Ohio, America: National Aeronautics and Space Administration) pp49−92
[39] Gupta R N, Yos J M, Thompson R A, Lee K P 1990 A Review of Reaction Rates and Thermodynamic and Transport Properties for an 11-species Air Model for Chemical and Thermal Nonequilibrium Calculations to 30000 K (Verginia, America: National Aeronautics and Space Administration) pp3−69
[40] Curtiss C F, Hirschfelder J O 1949 J. Chem. Phys. 17 550
Google Scholar
[41] Devoto R S 1967 Phys. Fluids 10 2105
Google Scholar
[42] Ghorui S, Das A K 2013 Phys. Plasmas 20 093504
Google Scholar
[43] Laricchiuta A, Bruno D, Capitelli M, Catalfamo C, Celiberto R, Colonna G, Diomede P, Giordano D, Gorse C, Longo S, Pagano D, Pirani F 2009 Eur. Phys. J. D 54 607
Google Scholar
[44] Park C 1990 Nonequilibrium Hypersonic Aerothermodynamics (New York: Wiley) p120
[45] Park C 2004 J. Thermophys. Heat Tr. 18 527
Google Scholar
[46] Millikan R C, White D R 1963 J. Chem. Phys. 39 3209
Google Scholar
[47] Lazdinis S, Petrie S L 1974 Phys. Fluids 17 1539
Google Scholar
[48] Park C 1984 Proceedings of the 19th Thermophysics Conference Snowmass, Colorado, America, June 25−28, 1984 pp3, 4
[49] Vincenti W G, Kruger C H 1965 Introduction to Physical Gas Dynamics (Malabar: Krieger)
[50] Kim M, Gülhan A, Boyd I D 2012 J. Thermophys. Heat Tr. 26 244
Google Scholar
[51] Bourdon A, Vervisch P 1997 Phys. Rev. E 55 4634
Google Scholar
[52] Appleton J, Bray K 1964 J. Fluid Mech. 20 659
Google Scholar
[53] Gnoffo P A, Gupta R N, Shinn J L 1989 Conservation Equations and Physical Models for Hypersonic Air Flows in Thermal and Chemical Nonequilibrium (Hampton, America: National Aeronautics and Space Administration) pp10−12
[54] Abe K, Kondoh T, Nagano Y 1994 Int. J. Heat Mass Trans. 37 139
Google Scholar
-
图 2 ICP炬计算网格和几何结构 (a) 电磁场与流场计算网格; (b) 等离子体炬几何结构
Fig. 2. Computational mesh and geometry of the inductively coupled plasma torch: (a) Computational mesh of electromagnetic- and flow-field; (b) geometric construction of the ICP torch.
图 3 等离子体炬内气体流线和速度矢量(上半部分)以及电子温度云图(下半部分)分布
Fig. 3. Distributions of streamlines and velocity vector (upper), and electron temperature (lower) in the torch.
图 4 等离子体流线(上半部分)和压力云图(下半部分)分布
Fig. 4. Distributions of streamlines (upper) and pressure contour (lower).
图 5 轴向洛伦兹力(上半部分)和径向洛伦兹力(下半部分)的分布
Fig. 5. Distributions of axial Lorentz force (upper) and radial Lorentz force (lower).
图 6 径向洛伦兹力(上半部分)和焦耳加热率(下半部分)的分布
Fig. 6. Distributions of Joule heating rate(lower) and radial Lorentz force (upper)
图 7 电场强度分布(虚部EI (上半部分)实部ER(下半部分))
Fig. 7. Distribution of electric-field intensity (imaginary part EI (upper) and real part ER (lower)).
图 8 电场强度Ei(上)和电子数密度ne(下)的分布
Fig. 8. Distribution of electric field intensity EI (upper) and electron number density ne (lower).
图 9 感应线圈中心(x = 68 mm)空气粒子径向摩尔分数分布
Fig. 9. Mole fraction of air species along the radial direction at the coil center x = 68 mm.
图 10 等离子体炬内平动温度(上半部分)和电子温度(下半部分)分布云图
Fig. 10. Distributions of translational (upper) and electronic temperatures (lower) in the torch.
表 1 空气化学反应模型
Table 1. Chemical reaction model of air.
r 反应物 生成物 Tf Tb Cr n θr 文献 离解/复合反应
(S1 = N2, O2, NO;
S2 = N, O; S3 = N2,
O2; S4 = NO, N, O)1—3 N2 + S1 $ \rightleftharpoons $ N + N + S1 $\sqrt {{T_{{\rm{tr}}}}{T_{{\rm{vib}}}}} $ ${T_{{\rm{tr}}}}$ 7.0 × 1021 –1.60 113200 [35] 4—5 N2 + S2 $ \rightleftharpoons $ N + N + S2 $\sqrt {{T_{{\rm{tr}}}}{T_{{\rm{vib}}}}} $ ${T_{{\rm{tr}}}}$ 3.0 × 1022 –1.60 113200 [35] 6—8 O2 + S1 $ \rightleftharpoons $ O + O + S1 $\sqrt {{T_{{\rm{tr}}}}{T_{{\rm{vib}}}}} $ ${T_{{\rm{tr}}}}$ 2.0 × 1021 –1.50 59500 [35] 9—10 O2 + S2 $ \rightleftharpoons $ O + O + S2 $\sqrt {{T_{{\rm{tr}}}}{T_{{\rm{vib}}}}} $ ${T_{{\rm{tr}}}}$ 1.0 × 1022 –1.50 59500 [35] 11—12 NO + S3 $ \rightleftharpoons $ N + O + S3 $\sqrt {{T_{{\rm{tr}}}}{T_{{\rm{vib}}}}} $ ${T_{{\rm{tr}}}}$ 5.0 × 1015 0.00 75500 [35] 13—15 NO + S4 $ \rightleftharpoons $ N + O + S4 ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 1.1 × 1017 0.00 75500 [35] 泽尔多维奇反应 16 N2 + O $ \rightleftharpoons $ NO + N ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 6.4 × 1017 –1.00 38400 [35] 17 NO + O $ \rightleftharpoons $ N + O2 ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 8.4 × 1012 0.00 19450 [35] 电量交换反应 18 N2 + N+ $ \rightleftharpoons $ N2+ + N ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 1.0 × 1012 0.50 12200 [35] 19 O2+ + O $ \rightleftharpoons $ O+ + O2 ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 4.0 × 1012 –0.09 18000 [35] 20 NO+ + O $ \rightleftharpoons $ NO + O+ ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 3.63 × 1015 –0.60 13000 [33] 21 O+ + N2 $ \rightleftharpoons $ N2+ + O ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 9.1 × 1011 0.36 22800 [35] 22 NO+ + O2 $ \rightleftharpoons $ O2+ + NO ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 2.4 × 1013 0.41 32600 [35] 23 NO+ + N $ \rightleftharpoons $ NO + N+ ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 1.0 × 1019 –0.93 61000 [33] 24 NO+ + O $ \rightleftharpoons $ N+ + O2 ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 1.0 × 1012 0.50 77200 [35] 副电离反应 25 N + N $ \rightleftharpoons $ N2+ + e– ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 4.4 × 107 1.50 67500 [35] 26 O + O $ \rightleftharpoons $ O2+ + e– ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 7.1 × 102 2.70 80600 [35] 27 N + O $ \rightleftharpoons $ NO+ + e– ${T_{{\rm{tr}}}}$ ${T_{{\rm{tr}}}}$ 8.8 × 108 1.00 31900 [35] 28 O2 + N2 $ \rightleftharpoons $ NO + NO+ + e– $\sqrt {{T_{\rm{e}}}{T_{{\rm{vib}}}}} $ ${T_{\rm{e}}}$ 1.38 × 1020 –1.84 141000 [33] 29 N2 + NO $ \rightleftharpoons $ N2 + NO+ + e– $\sqrt {{T_{\rm{e}}}{T_{{\rm{vib}}}}} $ ${T_{\rm{e}}}$ 2.20 × 1015 –0.35 108000 [33] 30 O2 + NO $ \rightleftharpoons $ O2 + NO+ + e– $\sqrt {{T_{\rm{e}}}{T_{{\rm{vib}}}}} $ ${T_{\rm{e}}}$ 8.80 × 1016 –0.35 108000 [33] 电子碰撞电离反应 31 N + e– $ \rightleftharpoons $ N+ + e– + e– ${T_{\rm{e}}}$ ${T_{\rm{e}}}$ 2.5 × 1034 –3.82 168600 [35] 32 O + e– $ \rightleftharpoons $ O+ + e– + e– ${T_{\rm{e}}}$ ${T_{\rm{e}}}$ 3.9 × 1033 –3.78 158500 [35] 
下载: 导出CSV
-
[1] Suzuki T, Fujita K, Ando K, Sakai T 2008 J. Thermophys. Heat Tr. 22 382
Google Scholar
[2] Suzuki T, Fujita K, Sakai T 2010 J. Thermophys. Heat Tr. 24 589
Google Scholar
[3] Yamada K, Miyatani S, Maeno H, Abe T 2013 Proceedings of 57th Space Sciences and Technology Conference Tottori, Japan, October 9−11, 2013 p2
[4] 熊举坤, 黄海涛, 2011 化工环保 31 119
Google Scholar
Xiong J K, Huang H T 2011 Environ. Prot. Chem. Indus. 31 119
Google Scholar
[5] 朱海龙, 叶高英, 程昌明, 杨发展, 童洪辉 2014 稀有金属材料与工程 43 2810
Zhu H L, Ye G Y, Cheng C M, Yang F Z, Tong H H 2014 Rare Metal Mat. Eng. 43 2810
[6] Watanabe T, Okumiya H 2004 Sci. Technol. Adv. Mater. 5 639
Google Scholar
[7] Miyatani S, 2014 Proceedings of the 58th Space Science and Technology Union Symposium Nagasaki, Japan, November 11−12, 2014 p2
[8] Reed T B 1961 J. Appl. Phys. 32 821
Google Scholar
[9] Mostaghimi J, Proulx P, Boulos M I 1987 J. Appl. Phys. 61 1753
Google Scholar
[10] Lei F, Li X, Liu Y, Liu D, Yang M, Yu Y 2018 AIP Adv. 8 015003
Google Scholar
[11] Yu M, Takahashi Y, Kihara H, Abe K, Yamada K, Abe T 2014 Plasma Sci. Technol. 16 930
Google Scholar
[12] 魏小龙, 徐浩军, 李建海, 林敏, 宋慧敏 2015 64 175201
Google Scholar
Wei X L, Xu H J, Li J H, Lin M, Song H M 2015 Acta Phys. Sin 64 175201
Google Scholar
[13] Xin Q, Su X, Alavi S, Wang B, Mostaghimi J 2018 Appl. Therm. Eng. 128 785
Google Scholar
[14] Morsli M E, Proulx P, Gravelle D 2011 Plasma Sources Sci. Technol. 20 015016
Google Scholar
[15] Wang Y N, Hou L J, Wang X 2002 Phys. Rev. Lett. 89 155001
Google Scholar
[16] Gao F, Li X, Zhao S, Wang Y 2012 Chin. Phys. B 21 075203
Google Scholar
[17] Yu M, Yamada K, Takahashi Y, Liu K, Zhao T 2016 Phys. Plasmas 23 123523
Google Scholar
[18] 朱海龙, 童洪辉, 杨发展, 程昌明, 叶高英 2013 高电压技术 39 1621
Google Scholar
Zhu H L, Tong H H, Yang F Z, Cheng C M, Ye G Y 2013 High Volt. Eng. 39 1621
Google Scholar
[19] Barnes R M, Nikdel S 1976 J. Appl. Phys. 47 3929
Google Scholar
[20] Mostaghimi J, Boulos M I 1989 Plasma Chem. Plasma Proc. 9 25
Google Scholar
[21] Punjabi S B, Joshi N K, Mangalvedekar H A, Lande B K, Das A K, Kothari D C 2012 Phys. Plasmas 19 012108
Google Scholar
[22] Punjabi S, Barve D, Joshi N, Das A, Kothari D, Ganguli A, Sahasrabhude S, Joshi J 2019 Processes 7 133
Google Scholar
[23] Mostaghimi J, Boulos M I 1990 J. Appl. Phys. 68 2643
Google Scholar
[24] Stewart R A, Vitello P, Graves D B 1994 J. Vac. Sci. Technol. B 12 478
Google Scholar
[25] Munafò A, Alfuhaid S A, Cambier J L, Panesi M 2015 J. Appl. Phys. 118 133303
Google Scholar
[26] Zhang W, Lani A, Panesi M 2016 Phys. Plasmas 23 073512
Google Scholar
[27] Degrez G, Abeele D V, Barbante P, Bottin B 2004 Int. J. Numer. Method H. 14 538
Google Scholar
[28] Sumi T, Fujita K, Kurotaki T, Ito T, Mizuno M, Ishida K 2005 Trans. Japan Soc. Aero. Space Sci. 48 40
Google Scholar
[29] Morsli M E, Proulx P 2007 J. Phys. D: Appl. Phys. 40 4810
Google Scholar
[30] Yu M, Yamada K, Liu K, Zhao T 2019 AIP Adv. 9 015120
Google Scholar
[31] Yu M, Liu K, Zhao T, Zhang Y 2016 J. Korean Phys. Soc. 69 1537
Google Scholar
[32] Yu M, Kihara H, Abe K I, Takahashi Y 2015 J. Korean Phys. Soc. 66 1833
Google Scholar
[33] Dunn M G, Kang S W 1973 Theoretical and Experimental Studies of Reentry Plasmas (Washionton DC: National Aeronautics and Space Administration) pp55−58
[34] Morsli M E, Proulx P 2007 J. Phys. D: Appl. Phys. 40 380
Google Scholar
[35] Park C, Jaffe R L, Partridge H 2001 J. Thermophys. Heat Tr. 15 76
Google Scholar
[36] Lenzner S, Auweter-Kurtz M, Heiermann J, Sleziona P 2000 J. Thermophys. Heat Tr. 14 388
Google Scholar
[37] Fujita K, Mizuno M, Ishida K, Ito T 2008 J. Thermophys. Heat Tr. 22 685
Google Scholar
[38] Yos J M 1963 Transport Properties of Nitrogen, Hydrogen, Oxygen, and Air to 30000 K (Ohio, America: National Aeronautics and Space Administration) pp49−92
[39] Gupta R N, Yos J M, Thompson R A, Lee K P 1990 A Review of Reaction Rates and Thermodynamic and Transport Properties for an 11-species Air Model for Chemical and Thermal Nonequilibrium Calculations to 30000 K (Verginia, America: National Aeronautics and Space Administration) pp3−69
[40] Curtiss C F, Hirschfelder J O 1949 J. Chem. Phys. 17 550
Google Scholar
[41] Devoto R S 1967 Phys. Fluids 10 2105
Google Scholar
[42] Ghorui S, Das A K 2013 Phys. Plasmas 20 093504
Google Scholar
[43] Laricchiuta A, Bruno D, Capitelli M, Catalfamo C, Celiberto R, Colonna G, Diomede P, Giordano D, Gorse C, Longo S, Pagano D, Pirani F 2009 Eur. Phys. J. D 54 607
Google Scholar
[44] Park C 1990 Nonequilibrium Hypersonic Aerothermodynamics (New York: Wiley) p120
[45] Park C 2004 J. Thermophys. Heat Tr. 18 527
Google Scholar
[46] Millikan R C, White D R 1963 J. Chem. Phys. 39 3209
Google Scholar
[47] Lazdinis S, Petrie S L 1974 Phys. Fluids 17 1539
Google Scholar
[48] Park C 1984 Proceedings of the 19th Thermophysics Conference Snowmass, Colorado, America, June 25−28, 1984 pp3, 4
[49] Vincenti W G, Kruger C H 1965 Introduction to Physical Gas Dynamics (Malabar: Krieger)
[50] Kim M, Gülhan A, Boyd I D 2012 J. Thermophys. Heat Tr. 26 244
Google Scholar
[51] Bourdon A, Vervisch P 1997 Phys. Rev. E 55 4634
Google Scholar
[52] Appleton J, Bray K 1964 J. Fluid Mech. 20 659
Google Scholar
[53] Gnoffo P A, Gupta R N, Shinn J L 1989 Conservation Equations and Physical Models for Hypersonic Air Flows in Thermal and Chemical Nonequilibrium (Hampton, America: National Aeronautics and Space Administration) pp10−12
[54] Abe K, Kondoh T, Nagano Y 1994 Int. J. Heat Mass Trans. 37 139
Google Scholar
下载:
计量
- 文章访问数: 11763
- PDF下载量: 131
- 被引次数: 0
