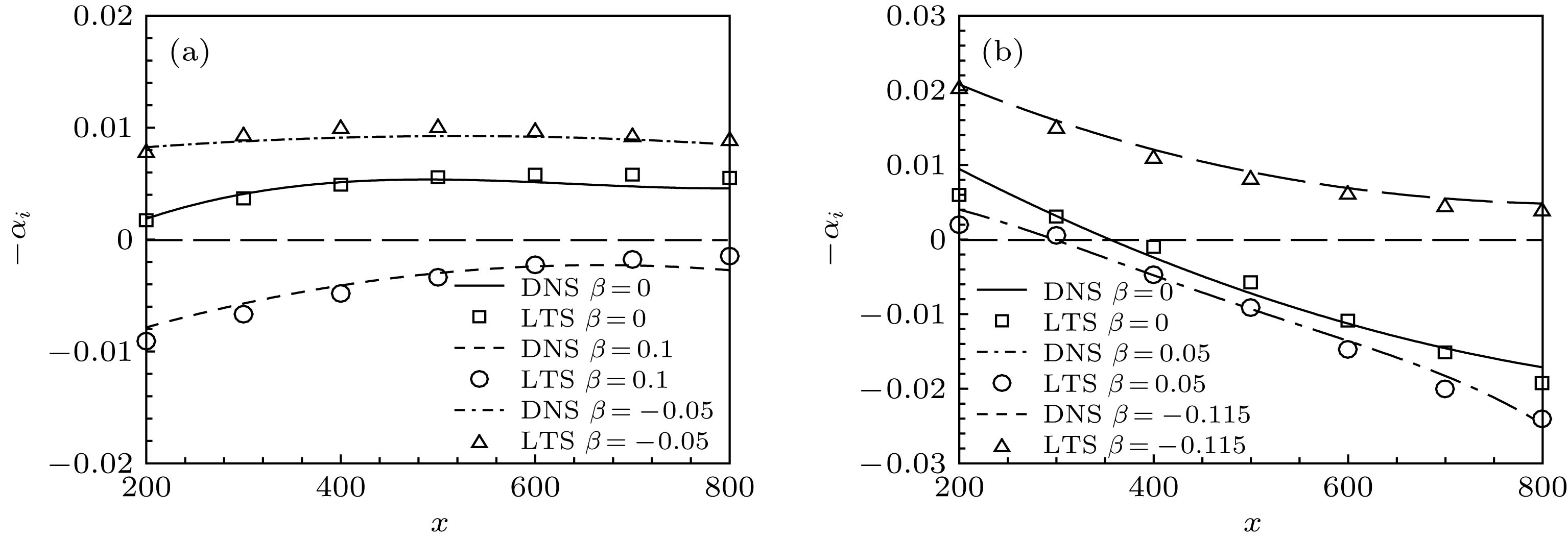
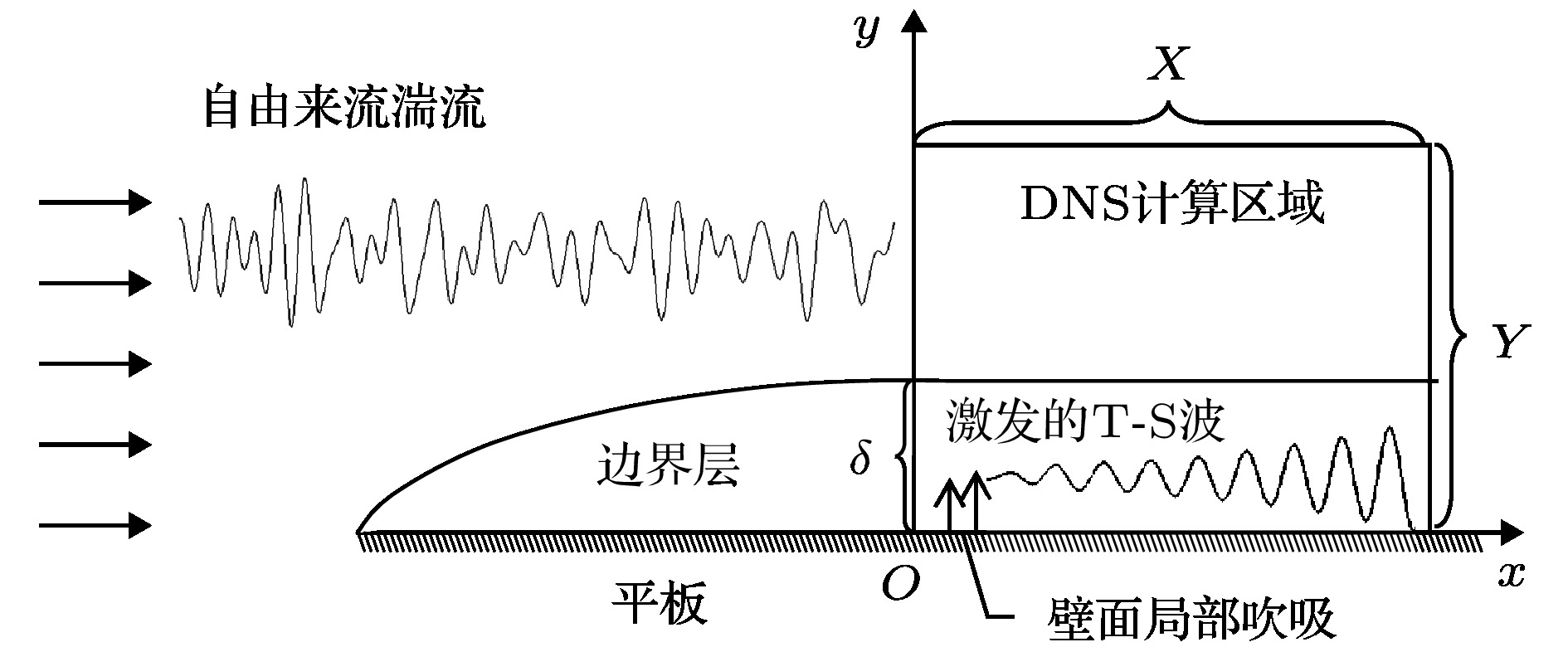
-
边界层感受性是层流向湍流转捩的初始阶段, 是实现边界层转捩预测和控制的关键环节. 研究结果表明, 边界层感受性问题不仅受到不同自由来流扰动条件, 壁面局部粗糙和局部吹吸的几何大小、形状和位置等参数的影响之外, 还受到一个重要参数压力梯度的作用. 因此, 本文数值研究在自由来流湍流分别与壁面局部吹入和吸出相互作用下压力梯度在激发边界层感受性过程起什么样的关键性作用, 从而揭示不同压力梯度对壁面局部吹入或吸出边界层内被激发出T-S波波包以及T-S波波包向前传播群速度的影响; 分别讨论逆压力梯度、顺压力梯度对边界层内被激发出的T-S波模态是起到加速增长的作用还是遏制增长的作用; 详细分析不同压力梯度对边界层内被激发出的T-S波的幅值、增长率、波长或波数、相速度以及特征形状函数的影响等. 这一问题的深入研究将为工程实践中各种叶片流体机械的设计和性能改善提供理论参考.Boundary-layer receptivity is the initial stage of the laminar-turbulent transition process, and plays a key role in predicting and controlling the transition. The present researches indicate that the boundary-layer receptivity is affected not only by the different sorts of free-stream disturbances or the size, shape and position of the wall localized roughness and blowing/suction, but also by the pressure gradient. Therefore, the local receptivity under the interaction between the free-stream turbulence and localized wall blowing/suction in the pressure-gradient boundary layer is studied in the present work, thus revealing the effect of the pressure gradient on the receptive process and the group speeds of the excited T-S wave packets under the interaction of the free-stream turbulence with localized wall blowing/suction in the boundary layer. High-order finite difference scheme is utilized to discretize the incompressible perturbation Navier-Stokes equation. A modified fourth-order Runge-Kutta scheme is used for time integration. The compact difference scheme based on non-uniform meshes is applied to the spatial discretization. The convective term is discretized by the fifth-order upwind compact scheme. The pressure gradient term is discretized by the sixth-order symmetric compact scheme. The viscosity term is discretized by the fifth-order symmetric compact scheme. Besides, the pressure Poisson equation is solved by the fourth-order scheme on the non-uniform meshes. The favorable or adverse pressure gradient promotes or suppresses the receptivity triggered by the interaction between free-stream turbulence and blowing/suction. And the blowing always induces a stronger receptivity than the suction in the same intensity. The initial amplitude of the T-S wave and wave packet excited in the adverse-pressure-gradient boundary layer are two orders larger than those excited in the favorable-pressure-gradient boundary layer. It is analyzed in detail that the favorable and adverse pressure gradient play a promoting or suppressing role in the growth of the excited T-S wave. Then the influences of the pressure gradient on the amplitudes, growth rates, wave numbers, phase speeds and shape functions of the excited T-S waves are investigated. The intensive research on receptivity in the pressure-gradient boundary layers provides a reference for designing the turbine machinery blades in the practical engineering.
-
Keywords:
- receptivity /
- pressure gradient /
- boundary-layer
[1] Goldstein M E 1983 J. Fluid. Mech. 127 59
Google Scholar
[2] Ruban A I 1984 Fluid Dynam. 19 709
[3] 陆昌根, 沈露予 2015 65 194701
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 65 194701
Google Scholar
[4] Shen L, Lu C, Zhu X 2019 Appl. Math. Mech. 40 851
Google Scholar
[5] Goldstein M E 1985 J. Fluid. Mech. 154 509
Google Scholar
[6] Saric W S, Hoos J A, Radeztsky R H 1991 Proceedings of the Symposium and Joint Fluids Engineering Conference, 1st Portland, U.S.A, June 23−27, 1991 p17
[7] Wiegel M, Wlezien R 1993 AIAA P. 3280
[8] Dietz A J 1999 J. Fluid. Mech. 378 291
Google Scholar
[9] Dietz A J 1998 AIAA J. 36 1171
Google Scholar
[10] Dietz A J 1996 AIAA P. 2083
[11] Wu X 2001 J. Fluid. Mech. 449 373
Google Scholar
[12] Wu X 2001 J. Fluid. Mech. 431 91
Google Scholar
[13] Shen L, Lu C 2016 Appl. Math. Mech. 37 929
Google Scholar
[14] Shen L, Lu C 2016 Appl. Math. Mech. 37 349
Google Scholar
[15] Würz W, Herr S, Wörner A, Rist U 2003 J. Fluid. Mech. 478 135
Google Scholar
[16] Shen L, Lu C 2018 Adv. Appl. Math. Mech. 10 735
Google Scholar
[17] 陆昌根, 沈露予 2015 64 224702
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 64 224702
Google Scholar
[18] Johnson M W, Pinarbasi 2014 Flow Turbul. Combu. 93 1
Google Scholar
[19] Jacobs R G 2001 J. Fluid. Mech. 428 185
Google Scholar
-
图 2 在压力梯度(a) βH = 0.1, (b) βH = 0和(c) βH = –0.05情况下壁面局部吹入边界层内被激发出T-S波波包沿流向呈现增长的演化趋势
Fig. 2. The streamwise evolutions of the excited T-S waves under the localized suction in the pressure-gradient boundary layers of (a) βH = 0.1, (b) βH = 0 and (c) βH = –0.05.
图 3 局部吹入和吸出边界层内被激发出T-S波包初始幅值AR与压力梯度的关系 (a) 吹入强度; (b) 吸出强度
Fig. 3. The relationships between the initial amplitudes of the excited T-S waves AR and the pressure-gradients in the localized blowing and suction boundary layers: (a) Blowing intensity; (b) suction intensity
图 4 不同压力梯度对壁面局部吹入边界层内被激发出的T-S波沿x向发展的影响 (a) F = 40; (b) F = 80
Fig. 4. The effect of different pressure gradients on x-direction evolutions of the excited T-S waves in the localized blowing boundary layers. (a) F = 40; (b) F = 80
图 5 壁面局部吹入边界层内被激发出T-S波的幅值AT-S沿x向的演化(t = 2400) (a) F = 40; (b) F = 80
Fig. 5. The x-direction evolutions of the amplitude of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.
图 6 壁面局部吹入边界层内被激发出T-S波的增长率(–αi)沿x向的演化(t = 2400) (a) F = 40; (b) F = 80
Fig. 6. The x-direction evolutions of the growth rate (–αi) of the excited T-S waves in the local blowing boundary layers (t = 2400): (a) F = 40; (b) F = 80.
图 7 在不同压力梯度情况下壁面局部吹入和吸出边界层内被激发出T-S波波包的初始幅值AR与局部吹吸强度q之间的关系
Fig. 7. The relationships between the initial amplitudes of the excited T-S waves AR and the localized blowing/suction intensity q in different pressure boundary layers
图 8 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的幅值沿y向演变的影响(x = 300)
Fig. 8. The effects of different pressure gradients on y-direction amplitude profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).
图 9 压力梯度对壁面局部吹入边界层内被激发出T-S波的特征形状函数的相位沿y向演变的影响(x = 300)
Fig. 9. The effects of different pressure gradients on y-direction phase profiles of the shape functions of the excited T-S waves in localized blowing boundary layers (x = 300).
表 1 压力梯度对边界层内被激发出T-S波波包向前传播的群速度(Cg)的影响
Table 1. The group speeds (Cg) of the excited T-S wave packets in the pressure-gradient boundary layers.
βH 0.3 0.1 0.05 0 –0.05 –0.1 Cg (吹入) 0.358 0.348 0.343 0.336 0.333 0.331 Cg (吸出) 0.356 0.347 0.341 0.334 0.332 0.329 
下载: 导出CSV
表 2 压力梯度边界层被激发出的T-S波的流向波数和相速度(αr, C)
Table 2. The streamwise wave numbers and phase speeds (αr, C) of the excited T-S wave packets in the pressure-gradient boundary layers.
βH –0.1 –0.05 0 0.05 0.1 F = 30(吹) (0.0977, 0.3071) (0.0960, 0.3125) (0.0949, 0.3161) (0.0934, 0.3212) (0.0915, 0.3279) F = 30(吸) (0.0984, 0.3049) (0.0967, 0.3102) (0.0956, 0.3138) (0.0943, 0.3181) (0.0923, 0.3250) F = 40(吹) (0.1262, 0.3169) (0.1251, 0.3197) (0.1240, 0.3226) (0.1218, 0.3284) (0.1204, 0.3322) F = 40(吸) (0.1269, 0.3152) (0.1257, 0.3182) (0.1248, 0.3205) (0.1226, 0.3263) (0.1210, 0.3306) F = 50(吹) (0.1533, 0.3262) (0.1522, 0.3285) (0.1514, 0.3303) (0.1489, 0.3357) (0.1470, 0.3401) F = 50(吸) (0.1541, 0.3245) (0.1531, 0.3266) (0.1521, 0.3287) (0.1497, 0.3340) (0.1477, 0.3385) F = 60(吹) (0.1792, 0.3348) (0.1784, 0.3363) (0.1772, 0.3386) (0.1755, 0.3419) (0.1735, 0.3458) F = 60(吸) (0.1799, 0.3335) (0.1792, 0.3348) (0.1780, 0.3371) (0.1763, 0.3403) (0.1744, 0.3440) F = 70(吹) (0.2047, 0.3419) (0.2036, 0.3438) (0.2020, 0.3465) (0.2004, 0.3493) (0.1985, 0.3526) F = 70(吸) (0.2055, 0.3406) (0.2043, 0.3426) (0.2028, 0.3451) (0.2012, 0.3479) (0.1993, 0.3512) F = 80(吹) (0.2287, 0.3498) (0.2279, 0.3510) (0.2267, 0.3529) (0.2249, 0.3557) (0.2234, 0.3581) F = 80(吸) (0.2295, 0.3486) (0.2286, 0.3500) (0.2276, 0.3515) (0.2261, 0.3538) (0.2244, 0.3565)
下载: 导出CSV
-
[1] Goldstein M E 1983 J. Fluid. Mech. 127 59
Google Scholar
[2] Ruban A I 1984 Fluid Dynam. 19 709
[3] 陆昌根, 沈露予 2015 65 194701
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 65 194701
Google Scholar
[4] Shen L, Lu C, Zhu X 2019 Appl. Math. Mech. 40 851
Google Scholar
[5] Goldstein M E 1985 J. Fluid. Mech. 154 509
Google Scholar
[6] Saric W S, Hoos J A, Radeztsky R H 1991 Proceedings of the Symposium and Joint Fluids Engineering Conference, 1st Portland, U.S.A, June 23−27, 1991 p17
[7] Wiegel M, Wlezien R 1993 AIAA P. 3280
[8] Dietz A J 1999 J. Fluid. Mech. 378 291
Google Scholar
[9] Dietz A J 1998 AIAA J. 36 1171
Google Scholar
[10] Dietz A J 1996 AIAA P. 2083
[11] Wu X 2001 J. Fluid. Mech. 449 373
Google Scholar
[12] Wu X 2001 J. Fluid. Mech. 431 91
Google Scholar
[13] Shen L, Lu C 2016 Appl. Math. Mech. 37 929
Google Scholar
[14] Shen L, Lu C 2016 Appl. Math. Mech. 37 349
Google Scholar
[15] Würz W, Herr S, Wörner A, Rist U 2003 J. Fluid. Mech. 478 135
Google Scholar
[16] Shen L, Lu C 2018 Adv. Appl. Math. Mech. 10 735
Google Scholar
[17] 陆昌根, 沈露予 2015 64 224702
Google Scholar
Lu C G, Shen L Y 2015 Acta Phys. Sin. 64 224702
Google Scholar
[18] Johnson M W, Pinarbasi 2014 Flow Turbul. Combu. 93 1
Google Scholar
[19] Jacobs R G 2001 J. Fluid. Mech. 428 185
Google Scholar
下载:
计量
- 文章访问数: 7725
- PDF下载量: 73
- 被引次数: 0
