液滴撞击液膜的穿越模式及运动特性

杨亚晶; 梅晨曦; 章旭东; 魏衍举; 刘圣华

doi:10.7498/aps.68.20190604

摘要

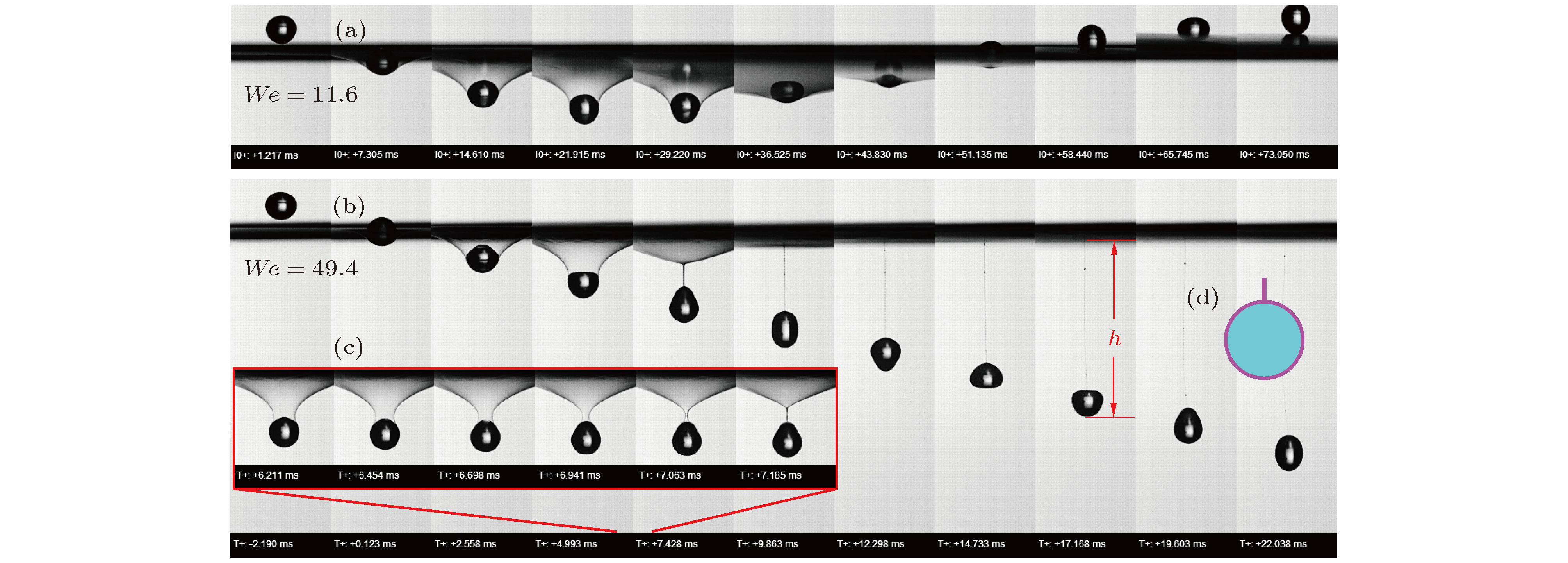
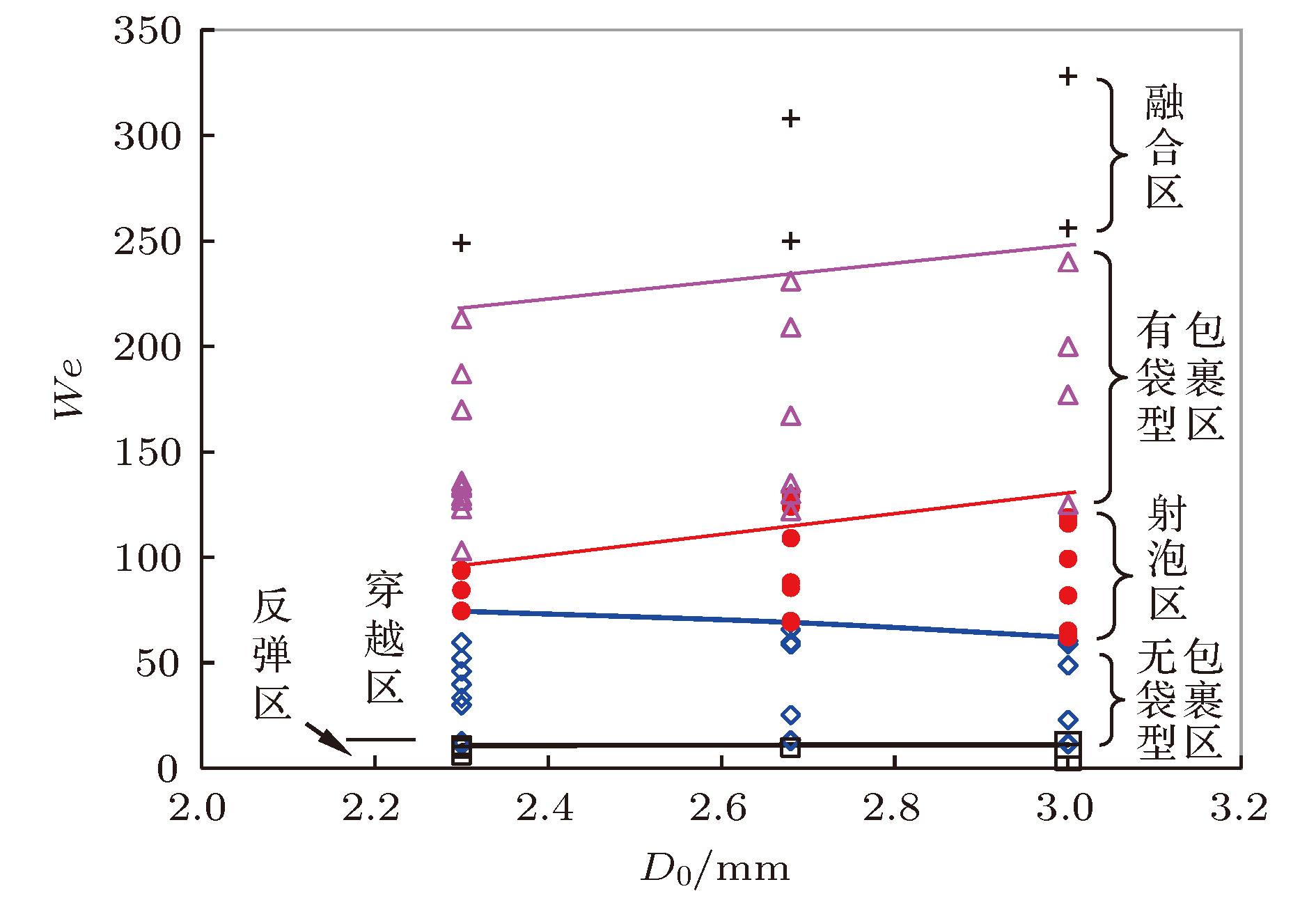
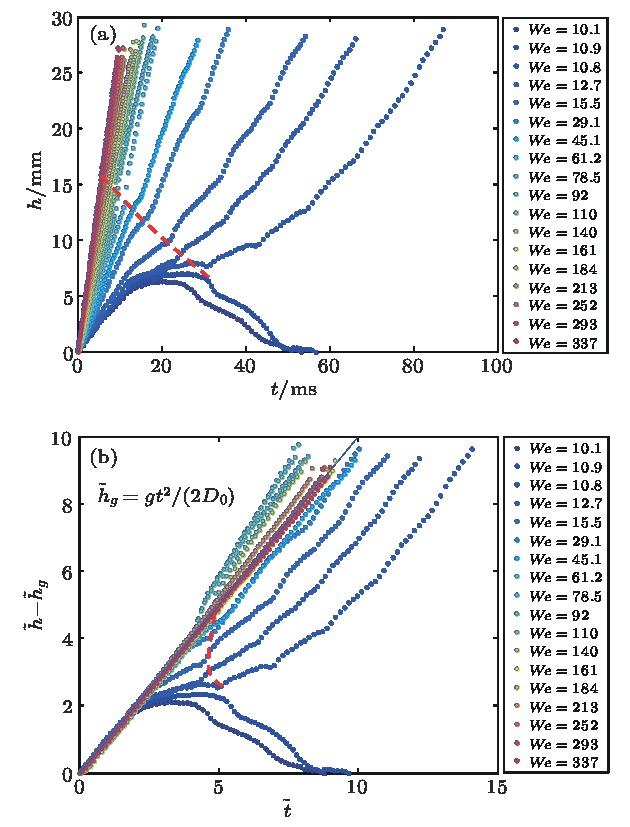
液滴撞击液膜是自然界中广泛存在的一种有趣的物理现象, 如雨滴撞击水坑中的雨泡, 啤酒穿过而不破坏杯中泡沫等, 科学家对此现象进行了一些研究, 但对其相互作用机理仍然认识不足. 本文利用高速摄像机记录液滴撞击肥皂膜的瞬态过程, 研究了不同韦伯数(We ∈ (10.8, 350))下液滴与液膜的相互作用过程、穿越模式及运动特性. 研究结果表明, 随着We的增加, 液滴从反弹过渡到穿越(临界We = 10.8), 穿越后, 根据液膜与液滴的作用形式, 又可细分为无袋型包裹、射泡、有袋型包裹和融合等四种不同穿越模式. 穿越后的液滴可形成“液滴-气垫-液膜”型复合液滴(We ∈ (120, 240))和表皮为微米厚溶液层的单相液滴(We ∈ (240, 350)). 根据气垫层厚度不同, 无袋型复合型液滴的表观表面张力为最外层液膜之表面张力, 而有袋型复合液滴则为3个气液界面的表面张力之和. 复合型液滴外层包膜可能破裂、剥落并产生射泡现象, 该现象发生在一定的We数区间内(We ∈ (60, 120)), 且该区间随着液滴直径的增加而增大. We数越大, 液滴穿越液膜过程中的速度损失越小, 液滴位移曲线越靠近理论曲线.

关键词:

液滴 /
液膜 /
撞击 /
穿越模式 /
射泡

Abstract

Droplet passing through a film is a ubiquitous phenomenon in nature, such as a rain drop impacting on a rain bubble in paddle and pouring beer onto the beer foam, etc. This phenomenon has not been sufficiently investigated and many interfacial interaction mechanisms are still unknown. In this paper, the passing modes and the kinematics of a droplet impacting on a soap film are studied with the help of a high-speed cameral. The impacting Weber number of the droplet varies from 10 to more than 350. The droplet position and velocity are extracted from the video by a self-designed Matlab codes. Experimental results show that the droplet may pass through the soap film in five modes, i.e., bouncing, bagless packaging, package peeling, bag packaging, and instaneous coalescence. A " drop-cushion-shell”-type compound droplet can be formatted in bag-[We ∈ (10.8, 60)] and bagless [We ∈ (120, 240)] packaging mode, while in the package peeling [We ∈ (60, 120)] and coalescence [We ∈ (240, 350)] mode it will form single phase droplets, however, with the surface coated with a soap solution layer (original soap film). Although compound droplets have three surfaces, i.e., the droplet’s original surface and the inner and outer surface of the soap film, the apparent surface tension for the bagless-packed droplet is just that of the soap solution, while for the bag-packed droplet it is the sum of the three surface tensions. The outer shell of the compound droplet may peel off and eject a bubble when the Weber number is in the certain range (We ∈ (60, 120) for droplet with D₀ = 3.0 mm), the lower limit decreases and the upper limit increases with the increase of the initial diameter of the droplets and thus expands the bubble-shooting range. The droplet performs a free fall motion, however, it is interfered by the soap film. The droplet can be stopped and rebounded when We < 10.8, and penetrate the film and start another free fall when We > 10.8. The velocity loss before and after the penetration decrease with impact velocity increasing, hence the motion of the higher We droplet is less retarded by the soap film, the motion curve approaches to the free fall curve. The approaching is not a linear but an accelerating behavior.

Keywords:

作者及机构信息

1.
西安交通大学航天学院, 机械结构强度与振动国家重点实验室, 西安　710049

2.
西安交通大学能源与动力工程学院, 西安　710049

通信作者: 魏衍举, weiyanju@xjtu.edu.cn

基金项目: 国家自然科学基金(批准号: 51576159)、国家自然科学基金重大研究计划(批准号: 91741110)、陕西省重点研发计划(批准号: 2019ZDLGY15-10)和陕西省交通新能源开发应用与汽车节能重点实验室(长安大学)开放基金(批准号: 300102229513)资助的课题.

Authors and contacts

1.
State Key Laboratory for Strength and Vibration of Machanical Structures, School of Aerospace Engineering, Xi’an Jiaotong University, Xi’an 710049, China

2.
School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an 710049, China

Corresponding author: Wei Yan-Ju, weiyanju@xjtu.edu.cn

Funds: Project Supported by the National Nature Science Foundation of China (Grant No. 51576159), the Major Research Plan of the National Natural Science Foundation of China (Grant No. 91741110), the Key R&D Program of Shaanxi Province, China (Grant No. 2019ZDLGY15-10), and Key Laboratory of Shaanxi Province for Development and Application of New Transportation Energy (Chang’an University) Open Funding Program (Grant No. 300102229513).

文章全文 : translate this paragraph

参考文献

[1]	Bartolo D, Jossereand C, Bonn D 2006 Phys. Rev. Lett. 96 124501 Google Scholar
[2]	Xu W, Leeladhar R, Kang Y T, Choi C H 2013 Langmuir 29 6032
[3]	Pan K L, Hung C Y 2010 Colloid Interface Sci. 352 186
[4]	Thoraval M J, Takehara K, Etoh T G, Thoroddsen S 2013 J. Fluid Mech. 724 234
[5]	Hu H B, Huang S H, Chen L B 2013 Chin. Phys. B 22 84702 Google Scholar
[6]	Pearson T, Maynes D, Webb B W 2012 Exp. Fluids 53 603
[7]	Aziz D S, Chandra S 2000 Int. J. Heat Mass Tran. 43 2841
[8]	Tran T, de Maleprade H, Sun C, Lohse D 2013 J. Fluid Mech. 726 R3 Google Scholar
[9]	Josserand C, Zaleski S 2003 Phys. Fluids 15 1650 Google Scholar
[10]	Eggers J, Fontelos M A, Josserand C, Zaleski S 2010 Phys. Fluids 22 062101 Google Scholar
[11]	Kim I, Wu X L 2010 Phys. Rev. E 82 026313 Google Scholar
[12]	Yarin A L 2006 Annu. Rev. Fluid Mech. 38 159
[13]	Fell D, Sokuler M, Lembach A, Eibach T F, Liu C J, Bonaccurso E, Auernhammer G K, Butt H J 2013 Colloid Polym. Sci. 291 1963 Google Scholar
[14]	Gilet T, Bush J W M 2009 J. Fluid Mech. 625 167 Google Scholar
[15]	Courbin L, Stone H A 2006 Phys. Fluids 18 91105 Google Scholar
[16]	Bai L, Xu W, Wu P F, Lin W J, Li C, Xu D L 2016 Colloids Surf. A 509 334 Google Scholar
[17]	Kim P G, Stone H A 2008 Europhys. Lett. 83 54001 Google Scholar
[18]	Dorbolo S, Caps H, Vandewalle N 2003 New J. Phys. 5 161 Google Scholar
[19]	Dorbolo S, Reyssat E, Vandewalle N 2005 Europhys. Lett. 69 966 Google Scholar
[20]	Thoroddsen S T, Takehara K, Etoh T G 2005 J. Fluid Mech. 530 295 Google Scholar
[21]	Hicks P D, Purvis R 2011 Phys. Fluids 23 062104 Google Scholar
[22]	Tang X Y, Saha A, Law C K, Sun C 2019 Phys. Fluids 31 013304 Google Scholar

施引文献

图 1 液滴撞击肥皂膜实验台架示意图

Fig. 1. Schematic diagram of the experimental platform.

下载: 全尺寸图片幻灯片

图 2 液滴的反弹与穿越

Fig. 2. Rebounding and penetration of droplets.

下载: 全尺寸图片幻灯片

图 3 穿越后复合液滴(D₀ = 3.0 mm)的直径振荡曲线与振荡周期　(a)液滴振荡; (b)振荡周期实验值与理论曲线对比

Fig. 3. Droplet (D₀ = 3.0 mm) oscillation phenomenon and its oscillation periods: (a) Droplet oscillation; (b) comparison of the experimental and theoretical oscillation periods.

下载: 全尺寸图片幻灯片

图 4 液滴包膜的剥落与射泡现象

Fig. 4. Shell peeling and bubble shooting.

下载: 全尺寸图片幻灯片

图 5 厚气垫层复合液滴的形成

Fig. 5. Formation of compound droplet with thick air cushion.

下载: 全尺寸图片幻灯片

图 6 液滴与液膜融合穿越现象

Fig. 6. Penetration by instant coalescence of droplet with film.

下载: 全尺寸图片幻灯片

图 7 不同We数下液滴穿越模式分布图

Fig. 7. Distribution of passing modes under various Weber numbers.

下载: 全尺寸图片幻灯片

图 8 液滴前锋的绝对位移与无量纲位移特性曲线(虚线为液膜液滴的分离时刻与分离高度)　(a)绝对位移; (b)无量纲位移

Fig. 8. Absolute and dimensionless displacements of the droplet front, the dashed line shows the departure height and time of the droplet and film: (a) Absolute displacement curves; (b) dimensionless displacement curves.

下载: 全尺寸图片幻灯片

map

[1]	Bartolo D, Jossereand C, Bonn D 2006 Phys. Rev. Lett. 96 124501 Google Scholar
[2]	Xu W, Leeladhar R, Kang Y T, Choi C H 2013 Langmuir 29 6032
[3]	Pan K L, Hung C Y 2010 Colloid Interface Sci. 352 186
[4]	Thoraval M J, Takehara K, Etoh T G, Thoroddsen S 2013 J. Fluid Mech. 724 234
[5]	Hu H B, Huang S H, Chen L B 2013 Chin. Phys. B 22 84702 Google Scholar
[6]	Pearson T, Maynes D, Webb B W 2012 Exp. Fluids 53 603
[7]	Aziz D S, Chandra S 2000 Int. J. Heat Mass Tran. 43 2841
[8]	Tran T, de Maleprade H, Sun C, Lohse D 2013 J. Fluid Mech. 726 R3 Google Scholar
[9]	Josserand C, Zaleski S 2003 Phys. Fluids 15 1650 Google Scholar
[10]	Eggers J, Fontelos M A, Josserand C, Zaleski S 2010 Phys. Fluids 22 062101 Google Scholar
[11]	Kim I, Wu X L 2010 Phys. Rev. E 82 026313 Google Scholar
[12]	Yarin A L 2006 Annu. Rev. Fluid Mech. 38 159
[13]	Fell D, Sokuler M, Lembach A, Eibach T F, Liu C J, Bonaccurso E, Auernhammer G K, Butt H J 2013 Colloid Polym. Sci. 291 1963 Google Scholar
[14]	Gilet T, Bush J W M 2009 J. Fluid Mech. 625 167 Google Scholar
[15]	Courbin L, Stone H A 2006 Phys. Fluids 18 91105 Google Scholar
[16]	Bai L, Xu W, Wu P F, Lin W J, Li C, Xu D L 2016 Colloids Surf. A 509 334 Google Scholar
[17]	Kim P G, Stone H A 2008 Europhys. Lett. 83 54001 Google Scholar
[18]	Dorbolo S, Caps H, Vandewalle N 2003 New J. Phys. 5 161 Google Scholar
[19]	Dorbolo S, Reyssat E, Vandewalle N 2005 Europhys. Lett. 69 966 Google Scholar
[20]	Thoroddsen S T, Takehara K, Etoh T G 2005 J. Fluid Mech. 530 295 Google Scholar
[21]	Hicks P D, Purvis R 2011 Phys. Fluids 23 062104 Google Scholar
[22]	Tang X Y, Saha A, Law C K, Sun C 2019 Phys. Fluids 31 013304 Google Scholar

[1]	刘贺, 杨亚晶, 唐玉凝, 魏衍举. 声致液滴失稳动力学研究. , 2024, 73(20): 204204. doi: 10.7498/aps.73.20240965
[2]	冯山青, 龚路远, 权生林, 郭亚丽, 沈胜强. 纳米液滴撞击高温平板壁的分子动力学模拟. , 2024, 73(10): 103106. doi: 10.7498/aps.73.20240034
[3]	董攀, 田昌, 李杰, 王韬, 于海涛, 苏明旭, 何佳龙, 石金水. 基于Mie散射在线测量真空弧放电液滴方法探索. , 2023, 72(8): 084203. doi: 10.7498/aps.72.20222406
[4]	彭家略, 郭浩, 尤天涯, 纪献兵, 徐进良. 液滴碰撞Janus颗粒球表面的行为特征. , 2021, 70(4): 044701. doi: 10.7498/aps.70.20201358
[5]	潘伶, 张昊, 林国斌. 纳米液滴撞击柱状固体表面动态行为的分子动力学模拟. , 2021, 70(13): 134704. doi: 10.7498/aps.70.20210094
[6]	魏衍举, 张洁, 邓胜才, 张亚杰, 杨亚晶, 刘圣华, 陈昊. 超声悬浮甲醇液滴的热诱导雾化现象. , 2020, 69(18): 184702. doi: 10.7498/aps.69.20200562
[7]	唐鹏博, 王关晴, 王路, 石中玉, 李源, 徐江荣. 单液滴正碰球面动态行为特性实验研究. , 2020, 69(2): 024702. doi: 10.7498/aps.69.20191141
[8]	黄虎, 洪宁, 梁宏, 施保昌, 柴振华. 液滴撞击液膜过程的格子Boltzmann方法模拟. , 2016, 65(8): 084702. doi: 10.7498/aps.65.084702
[9]	王松岭, 刘梅, 王思思, 吴正人. 随时间变化的非平整壁面对液膜表面波演化特性的影响. , 2015, 64(1): 014701. doi: 10.7498/aps.64.014701
[10]	郭亚丽, 魏兰, 沈胜强, 陈桂影. 双液滴撞击平面液膜的流动与传热特性. , 2014, 63(9): 094702. doi: 10.7498/aps.63.094702
[11]	张文彬, 廖龙光, 于同旭, 纪爱玲. 溶液液滴蒸发变干的环状沉积. , 2013, 62(19): 196102. doi: 10.7498/aps.62.196102
[12]	何峰, 王志军, 黄义辉, 叶鹏, 王锦程. 存在液膜的毛细蒸发过程研究. , 2013, 62(24): 246401. doi: 10.7498/aps.62.246401
[13]	李大鸣, 王志超, 白玲, 王笑. 液滴撞击孔口附近壁面运动过程的模拟研究. , 2013, 62(19): 194704. doi: 10.7498/aps.62.194704
[14]	梁刚涛, 郭亚丽, 沈胜强. 液滴撞击液膜的射流与水花形成机理分析. , 2013, 62(2): 024705. doi: 10.7498/aps.62.024705
[15]	马理强, 常建忠, 刘汉涛, 刘谋斌. 液滴溅落问题的光滑粒子动力学模拟. , 2012, 61(5): 054701. doi: 10.7498/aps.61.054701
[16]	张明焜, 陈硕, 尚智. 带凹槽的微通道中液滴运动数值模拟. , 2012, 61(3): 034701. doi: 10.7498/aps.61.034701
[17]	马理强, 刘谋斌, 常建忠, 苏铁熊, 刘汉涛. 液滴冲击液膜问题的光滑粒子动力学模拟. , 2012, 61(24): 244701. doi: 10.7498/aps.61.244701
[18]	毕菲菲, 郭亚丽, 沈胜强, 陈觉先, 李熠桥. 液滴撞击固体表面铺展特性的实验研究. , 2012, 61(18): 184702. doi: 10.7498/aps.61.184702
[19]	石自媛, 胡国辉, 周哲玮. 润湿性梯度驱动液滴运动的格子Boltzmann模拟. , 2010, 59(4): 2595-2600. doi: 10.7498/aps.59.2595
[20]	郭加宏, 戴世强, 代钦. 液滴冲击液膜过程实验研究. , 2010, 59(4): 2601-2609. doi: 10.7498/aps.59.2601

计量

文章访问数: 11698
PDF下载量: 169
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

液滴撞击液膜的穿越模式及运动特性