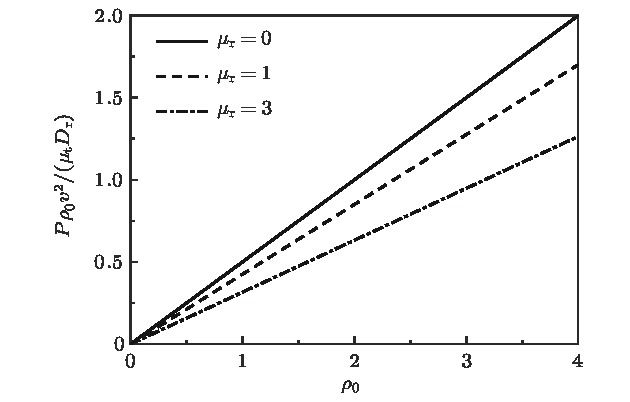
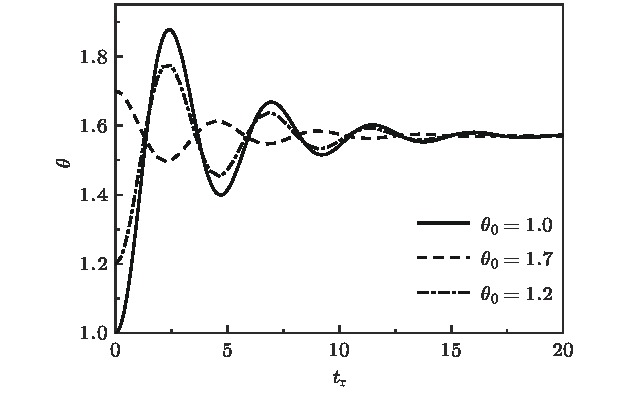
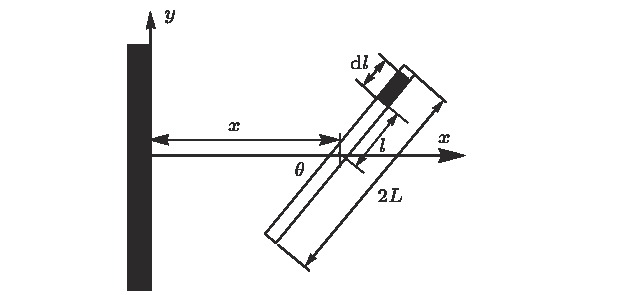
-
自驱动粒子系统由可以从环境获取能量并转化为主动运动的粒子组成, 与经典的被动粒子系统有显著的区别. 对于这样的主动系统, 是否存在经典的物态方程这一问题引起了广泛的关注. 最近的研究以谐振子势场中的主动系统为模型, 研究了物态方程的适定性. 与之不同, 本文探讨了封闭空间的主动粒子系统, 在墙壁与粒子间存在双电层相互作用下, 系统物态方程存在的条件及具体形式. 结果表明, 壁面压强与主动粒子的形状有关, 当有墙壁施加力矩于主动粒子时, 在力矩作用下粒子趋向转向平行于壁面的平衡态, 而壁面-粒子相互作用强度增加使平行取向的趋势增强, 从而使系统压强降低. 此时压强和壁面的关联意味着主动系统没有通用的物态方程. 同时讨论了在壁面-粒子相互作用强度极小或极大的情况下压强的形式, 通过定义有效温度, 给出了主动系统与理想气体类似的物态方程. 此外研究发现, 对于不同粒子, 其形状偏离转动对称性的程度是影响主动粒子压强的关键因素. 该结果对当前主动系统热力学性质的研究提供了一定的参考, 并为更复杂的相互作用势下研究主动系统的热力学性质提供了基础.Self-driven particle systems consist of particles that can extract energy from the environment and transform into active motion, and thus are significantly different from the classical passive particle systems. For such an active system, the question of whether there is a classical equation of state (EOS) has caused spreading concern. Recent studies analyzed the validity of the EOS of an active system under the harmonic potential (Solon et. al, 2015 Nature Physics, 11 673). In contrast, this paper explores the conditions for and the specific forms of the EOS of an active system under electric double-layer interaction between the wall and the particles. The results show that the wall pressure is related to the shape of the active particles. When a wall exerts a moment on the active particles, the particles orientation turns to the equilibrium state parallel to the wall surface under the action of the moment, and the increase of the wall-particle interaction strength enhances the parallel-orientation trend, which reduces the system pressure. The association of pressure and wall means that the active system does not have a general equation of state. In the case where the wall-particle interaction intensity is extremely small or extremely large, by defining the effective temperature, the active system has an equation of state similar to that of the ideal gas. In addition, it is found that the extent of the shape of particles deviating from the rotational symmetry is a key factor affecting the pressure of active particles. The research results provide a reference for the study of the current active system equilibrium properties, and provide a basis for studying the thermodynamic properties of active systems under more complex interaction potentials.
-
Keywords:
- active matter /
- equation of state /
- electric double layer interaction /
- pressure
[1] Paxton W F, Kistler K C, Olmeda C C, Ayusman, Angelo S K, Cao Y Y, Mallouk T E, Lammert P E, Crespi V H 2004 J. Am. Chem. Soc. 126 3424
Google Scholar
[2] Deseigne J, Leonard S, Dauchot O, Chate H 2012 Soft Matter 8 5629
Google Scholar
[3] Martin A 2008 Biotechniques 44 564
Google Scholar
[4] Tim S, Chen D T N, Stephen J D, Michael H, Zvonimir D 2012 Nature 491 431
Google Scholar
[5] Scot K C, James L M 2000 Nature 407 1026
Google Scholar
[6] Karsten K, Jülicher F 2000 Phys. Rev. Lett. 85 1778
Google Scholar
[7] Grimm V, Revilla E, Berger U, Jeltsch F, Mooij W, Steven F, Hans-Hermann T, Jacob W, Thorsten W, Donald L D 2005 Science 310 987
Google Scholar
[8] Gregoire G, Chate H 2004 Phys. Rev. Lett. 92 025702
Google Scholar
[9] Lifshitz E M, Pitaevskii L P 1999 Physical Kinetics (Beijing: Beijing World Publishing Corporation) pp89− 92
[10] Loi D, Mossa S, Cugliandolo L F 2008 Phys. Rev. E 77 051111
Google Scholar
[11] Shen T, Wolynes P G 2005 Phys. Rev. E 72 041927
Google Scholar
[12] Wang S, Wolynes P G 2011 Proc. Natl. Acad. Sci. USA 108 15184
Google Scholar
[13] Solon A P, Stenhammar J, Wittkowski R, Kardar M, Kafri Y, Cates M E, Tailleur J 2015 Phys. Rev. Lett. 114 198301
Google Scholar
[14] Takatori S C, Yan W, Brandy J F 2014 Phys. Rev. Lett. 113 028103
Google Scholar
[15] Yang X B, Manning L M, Marchetti M C 2014 Soft Matter 10 6477
Google Scholar
[16] Takatori S C, Dier R D, Vermant J, Brady J F 2016 Nat. Commun. 7 10694
Google Scholar
[17] Ginot F, Theurkauff I, Levis D, Ybert C, Bocquet L, Berthier L, Cottin-Bizonne C 2015 Phys. Rev. X 5 011004
[18] Foss D R, Brandy J F 2000 J. Rheol. 44 629
Google Scholar
[19] Liu C L, Fu X F, Liu L Z, Ren X J, Chau Carlos K L, Li S H, Xiang L, Zeng H L, Chen G H, Tang L H, Lenz P, Cui X D, Huang W, Hwa T, Huang J D 2011 Science 334 238
Google Scholar
[20] Baskaran A, Marchetti M C 2008 Phys. Rev. Lett. 101 268101
Google Scholar
[21] Solon A P, Fily Y, Baskaran A, Cates M E, Kafri Y, Kardar M, Tailleur J 2015 Nat. Phys. 11 673
Google Scholar
[22] Junot G, Briand G, Ledesma-Alonso R, Dauchot O 2017 Phys. Rev. Lett. 119 028002
Google Scholar
[23] 伊斯雷尔奇维利 著 (王晓琳, 唐元晖, 卢滇南 译) 2011 分子间力和表面力 (北京: 科学出版社) 第280−286页
Israelachvili (translated by Wang X L, Tang Y H, Lu D N) 2011 Intermolecular and Surface Forces (Beijing: Science Press) pp282−286 (in Chinese)
[24] 徐锡申, 张万箱等 1986 实用物态方程理论导引 (北京: 科学出版社) 第87−90页
Xu X S, Zhang W X, et al 1986 Theorey of Practical Equation of State (Beijing: Science Press) pp87−90 (in Chineses)
[25] Fily Y, Marchetti M 2012 Phys. Rev. Lett. 108 235702
Google Scholar
[26] Tailleur J, Cates M 2008 Phys. Rev. Lett. 100 218103
Google Scholar
[27] Palacci J, Cottin-Bizonne C, Ybert C, Bocquet L 2010 Phys. Rev. Lett. 105 088304
Google Scholar
[28] Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T 2013 Phys. Rev. Lett. 110 238301
Google Scholar
[29] Marchetti M, Joanny J, Ramaswamy S, Liverpool T, Prost J, Rao M, Simha R 2013 Rev. Mod. Phys. 85 1143
Google Scholar
[30] Bechinger C, Leonardo R D, Lowen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[31] Saragosti J, Silberzan P, Buguin A 2012 Plos One 7 35412
Google Scholar
[32] Alexandre S P, Fily Y, Baskaran A, Cates M E, Kafri Y, Kardar M, Tailleur J 2015 Nat. Phys. 11 673 (Supplementary information)
[33] Ho C C, Keller A, Odell J A, Ottewill R H 1993 Colloid Polym. Sci. 271 469
Google Scholar
[34] Han Y, Alsayed A M, Nobili M, Zhang J, Lubensky T C, Yodh A G 2006 Science 314 626
Google Scholar
-
图 1 主动系统粒子示意图, 粒子质心距离壁面水平距离为x, 粒子长度为2L, 取向角为θ
Fig. 1. Schematic diagram of the active particle, the horizonal distance between the wall and the centroid of the particle is x, the length of the particle is 2L and the orienting angle is θ.
图 2 等效压强随约化相互作用强度Zr的变化
Fig. 2. Effective pressure as the function of reduced interaction intensity.
图 3 等效压强随主动粒子约化长度Lr的变化
Fig. 3. Effective pressure as the function of reduced length of active particle.
图 4 力矩和压强随三种粒子结构常数的变化
Fig. 4. The variations of the torques and the pressures as a function of structure constants of the three kinds of particle.
图 5 对于不同的转动迁移率, 压强随粒子数密度的变化
Fig. 5. The variations of pressures as a function of particle number density for different rotational mobilities.
图 6 对于不同的初始角坐标, 粒子取向角随时间的演化, 约化阻尼系数αr = 0.5
Fig. 6. For different initial angular coordinates, the evolutions of orienting angles. Reduced damping coefficient αr = 0.5.
表 1 不同类型主动系统粒子运动参数取值说明
Table 1. Description of particle motion parameters of different types of active systems.
下载: 导出CSV
-
[1] Paxton W F, Kistler K C, Olmeda C C, Ayusman, Angelo S K, Cao Y Y, Mallouk T E, Lammert P E, Crespi V H 2004 J. Am. Chem. Soc. 126 3424
Google Scholar
[2] Deseigne J, Leonard S, Dauchot O, Chate H 2012 Soft Matter 8 5629
Google Scholar
[3] Martin A 2008 Biotechniques 44 564
Google Scholar
[4] Tim S, Chen D T N, Stephen J D, Michael H, Zvonimir D 2012 Nature 491 431
Google Scholar
[5] Scot K C, James L M 2000 Nature 407 1026
Google Scholar
[6] Karsten K, Jülicher F 2000 Phys. Rev. Lett. 85 1778
Google Scholar
[7] Grimm V, Revilla E, Berger U, Jeltsch F, Mooij W, Steven F, Hans-Hermann T, Jacob W, Thorsten W, Donald L D 2005 Science 310 987
Google Scholar
[8] Gregoire G, Chate H 2004 Phys. Rev. Lett. 92 025702
Google Scholar
[9] Lifshitz E M, Pitaevskii L P 1999 Physical Kinetics (Beijing: Beijing World Publishing Corporation) pp89− 92
[10] Loi D, Mossa S, Cugliandolo L F 2008 Phys. Rev. E 77 051111
Google Scholar
[11] Shen T, Wolynes P G 2005 Phys. Rev. E 72 041927
Google Scholar
[12] Wang S, Wolynes P G 2011 Proc. Natl. Acad. Sci. USA 108 15184
Google Scholar
[13] Solon A P, Stenhammar J, Wittkowski R, Kardar M, Kafri Y, Cates M E, Tailleur J 2015 Phys. Rev. Lett. 114 198301
Google Scholar
[14] Takatori S C, Yan W, Brandy J F 2014 Phys. Rev. Lett. 113 028103
Google Scholar
[15] Yang X B, Manning L M, Marchetti M C 2014 Soft Matter 10 6477
Google Scholar
[16] Takatori S C, Dier R D, Vermant J, Brady J F 2016 Nat. Commun. 7 10694
Google Scholar
[17] Ginot F, Theurkauff I, Levis D, Ybert C, Bocquet L, Berthier L, Cottin-Bizonne C 2015 Phys. Rev. X 5 011004
[18] Foss D R, Brandy J F 2000 J. Rheol. 44 629
Google Scholar
[19] Liu C L, Fu X F, Liu L Z, Ren X J, Chau Carlos K L, Li S H, Xiang L, Zeng H L, Chen G H, Tang L H, Lenz P, Cui X D, Huang W, Hwa T, Huang J D 2011 Science 334 238
Google Scholar
[20] Baskaran A, Marchetti M C 2008 Phys. Rev. Lett. 101 268101
Google Scholar
[21] Solon A P, Fily Y, Baskaran A, Cates M E, Kafri Y, Kardar M, Tailleur J 2015 Nat. Phys. 11 673
Google Scholar
[22] Junot G, Briand G, Ledesma-Alonso R, Dauchot O 2017 Phys. Rev. Lett. 119 028002
Google Scholar
[23] 伊斯雷尔奇维利 著 (王晓琳, 唐元晖, 卢滇南 译) 2011 分子间力和表面力 (北京: 科学出版社) 第280−286页
Israelachvili (translated by Wang X L, Tang Y H, Lu D N) 2011 Intermolecular and Surface Forces (Beijing: Science Press) pp282−286 (in Chinese)
[24] 徐锡申, 张万箱等 1986 实用物态方程理论导引 (北京: 科学出版社) 第87−90页
Xu X S, Zhang W X, et al 1986 Theorey of Practical Equation of State (Beijing: Science Press) pp87−90 (in Chineses)
[25] Fily Y, Marchetti M 2012 Phys. Rev. Lett. 108 235702
Google Scholar
[26] Tailleur J, Cates M 2008 Phys. Rev. Lett. 100 218103
Google Scholar
[27] Palacci J, Cottin-Bizonne C, Ybert C, Bocquet L 2010 Phys. Rev. Lett. 105 088304
Google Scholar
[28] Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T 2013 Phys. Rev. Lett. 110 238301
Google Scholar
[29] Marchetti M, Joanny J, Ramaswamy S, Liverpool T, Prost J, Rao M, Simha R 2013 Rev. Mod. Phys. 85 1143
Google Scholar
[30] Bechinger C, Leonardo R D, Lowen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[31] Saragosti J, Silberzan P, Buguin A 2012 Plos One 7 35412
Google Scholar
[32] Alexandre S P, Fily Y, Baskaran A, Cates M E, Kafri Y, Kardar M, Tailleur J 2015 Nat. Phys. 11 673 (Supplementary information)
[33] Ho C C, Keller A, Odell J A, Ottewill R H 1993 Colloid Polym. Sci. 271 469
Google Scholar
[34] Han Y, Alsayed A M, Nobili M, Zhang J, Lubensky T C, Yodh A G 2006 Science 314 626
Google Scholar
下载:
计量
- 文章访问数: 6988
- PDF下载量: 39
- 被引次数: 0
