化学复合率对激发赤道等离子体泡影响的数值模拟

姜春华; 赵正予

doi:10.7498/aps.68.20190173

摘要

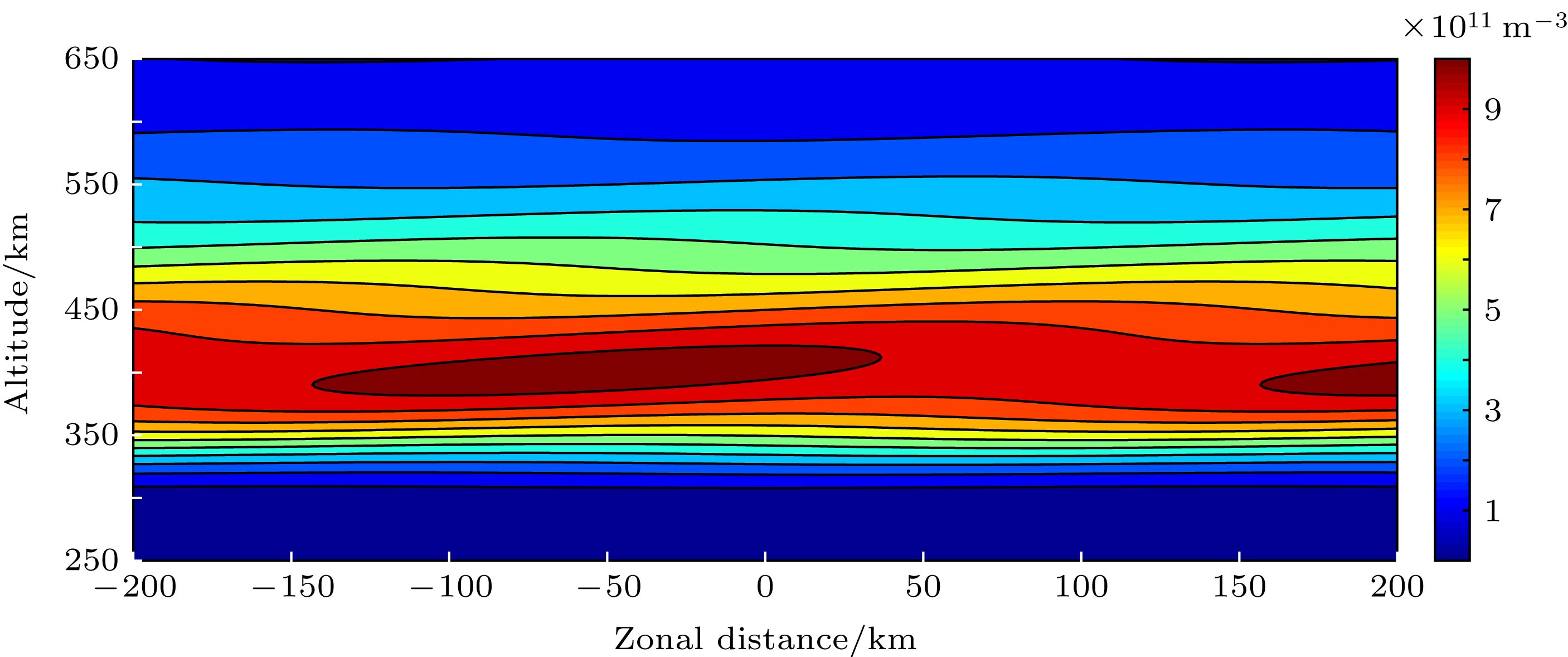
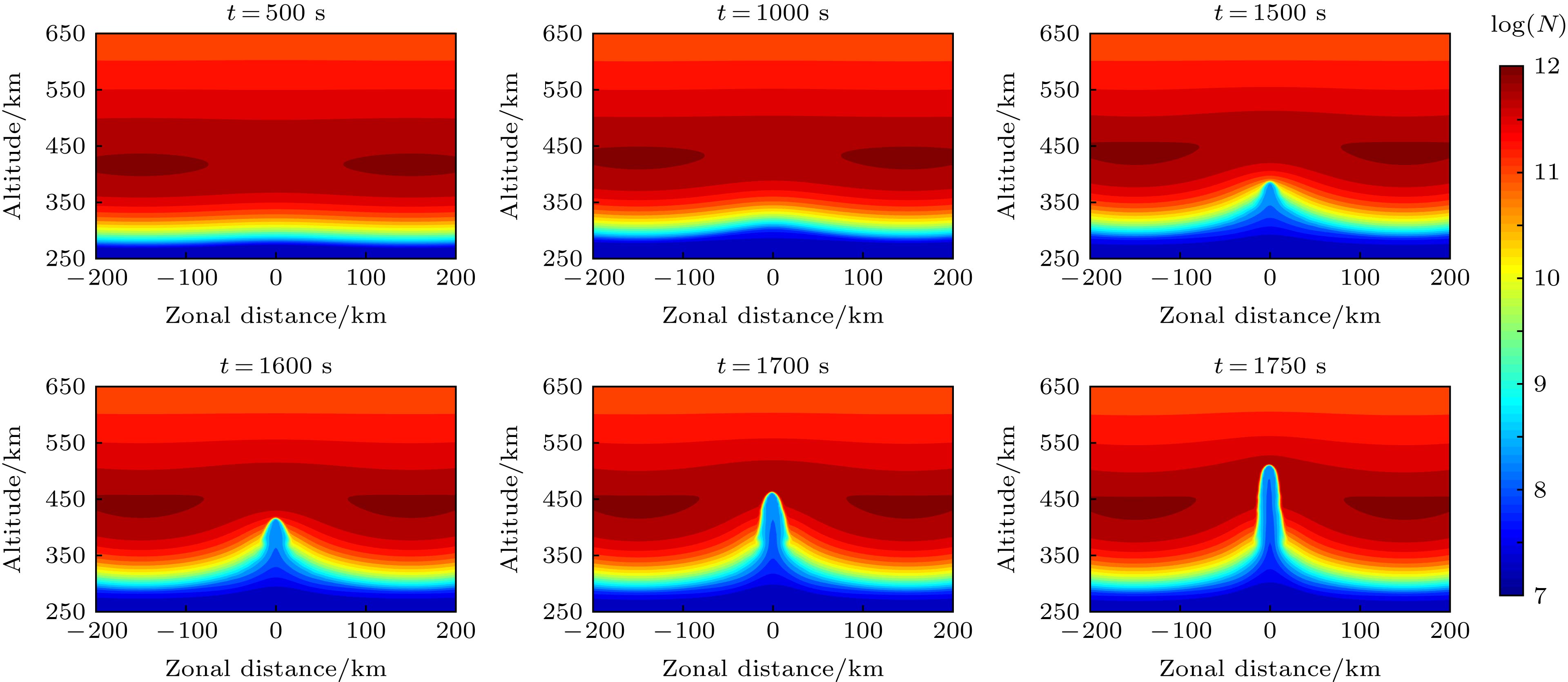
本文模拟研究了背景电离层在一维和二维扰动下产生等离子体泡的过程, 在模拟过程中引入行进式电离层扰动(traveling ionosphere disturbances, TIDs)模型激发生成电子密度的二维扰动, 同时通过改变化学复合率来研究不同复合率对等离子体泡结构形态的影响. 模拟结果表明, 复合率对等离子体泡的生成速度有较大影响, 复合率越大, 激发等离子体泡所需时间越长. 另外, 在二维扰动情况下电离层生成等离子体泡的速度要比一维扰动情况下的速度慢. 在一维扰动情况下, 不同复合率对等离子体泡结构形态影响不大, 而在TIDs激发的等离子体泡中, 不同复合率对等离子体泡的结构形态有较大影响. 在较小复合率的情况下, TIDs激发的等离子体泡可以产生分叉结构, 并伴有大量小尺度的等离子体泡结构, 同时模拟结果存在等离子体泡底部收缩现象. 模拟结果还表明, 当存在大量小尺度等离子体泡时, 单个等离子体泡周围的极化电场方向在非线性的演化过程中可能会发生变化, 因此并不是所有底部等离子体泡都能够抬升到电离层顶部, 只有其周围极化电场方向一直是东向的等离子体泡, 才能够进一步抬升到电离层顶部.

关键词:

Abstract

Plasma bubbles in the ionosphere have a significant effect on radio wave communication and navigation. Under the worst condition, it will fail to function the systems relying on the ionosphere. On the other hand, the physical mechanisms of evolution and diurnal variations of the plasma bubbles in the ionosphere are still unclear. Therefore, it is still worthy to simulate the plasma bubbles in the ionosphere for radio wave propagation and science. In this study, the equatorial plasma bubbles induced by one- and two- dimensional disturbance in the ionosphere are simulated, where traveling ionospheric disturbance (TID) is used to produce the two-dimensional disturbance in the ionosphere. The dispersion relationship of gravity wave is used to represent the corresponding wavelength of TID in this study. More importantly, we investigate the effect of recombination rate on the development of plasma bubbles by numerical simulation. The simulation results show that the recombination rate of the plasma in the ionosphere has a significant effect on the development of plasma bubbles. The greater the recombination rate, the more time it takes to produce the plasma bubbles. For one-dimensional disturbance in the ionosphere, there is no significant effect in the structure of plasma bubbles for the recombination rate of the plasma. However, the recombination rate plays a significant effect on the structure of plasma bubbles induced by TID. When the recombination rate is less in numerical simulation, the complex structure including bifurcation, plume-like structures, and pinching of plasma bubbles can occur in the development of bubbles. In contrast, the structure of plasma bubbles is simpler when the recombination rate is greater in simulation. As a result, the recombination rate of the plasma is a significant factor for simulating the plasma bubbles in the ionosphere. The greater recombination rate can result in the slowing down of equatorial plasma bubbles and the simplifying the structure of the bubbles as well. In addition, it is found that not all of plasma bubbles at the bottom of the ionosphere can grow to the top of the ionosphere when many bubbles occur on the bottom side. The direction of the polarization electric field near the bubbles can be changed in the non-linear development of the bubbles. Therefore, only the bubbles where the polarization electric field is always eastward can develop to the topside.

Keywords:

作者及机构信息

武汉大学电子信息学院, 武汉　430072

通信作者: 姜春华, chuajiang@whu.edu.cn

基金项目: 国家自然科学基金青年科学基金(批准号: 41604133)资助的课题

Authors and contacts

School of Electronic Information, Wuhan University, Wuhan 430072, China

Corresponding author: Jiang Chun-Hua, chuajiang@whu.edu.cn

Funds: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 41604133)

文章全文 : translate this paragraph

参考文献

[1]	Dungey J W 1956 J. Atmos. Terr. Phys. 9 304 Google Scholar
[2]	Abdu M A 2001 J. Atmos. Terr. Phys. 63 869 Google Scholar
[3]	Tsunoda R T, Yamamoto M, Tsugawa T, Hoang T L, Ram S T, Thampi S V, Chau H D, Nagatsuma T 2011 Geophys. Res. Lett. 38 L20102 Google Scholar
[4]	Sekar R, Suhasini R, Raghavarao R 1994 J. Geophys. Res. 99 2205 Google Scholar
[5]	Huang C S, Kelley M C 1996 J. Geophys. Res. Space Physics 101 303 Google Scholar
[6]	Hysell D L, Kelley M C, Swartz W E, Woodman R F 1990 J. Geophys. Res. Space Physics 95 17253 Google Scholar
[7]	Huang C S, Kelley M C 1996 J. Geophys. Res. Space Physics 101 293 Google Scholar
[8]	Scannapieco A J, Ossakow S L 1976 Geophys. Res. Lett. 3 451 Google Scholar
[9]	Zalesak S T, Ossakow S L 1980 J. Geophys. Res. 85 2131 Google Scholar
[10]	Zalesak S T, Ossakow S L, Chaturvedi P K 1982 J. Geophys. Res. 87 151 Google Scholar
[11]	谢红, 肖佐 1993 地球 36 18 Google Scholar Xie H, Xiao Z 1993 Chinese J. Geophys. 36 18 Google Scholar
[12]	高泽, 方涵先, 汪四成, 杨升高 2017 地球 60 470 Google Scholar Gao Z, Fang H X, Wang S C, Yang S G 2017 Chinese J. Geophys. 60 470 Google Scholar
[13]	Huba J D, Joyce G, Krall J 2008 Geophys. Res. Lett. 35 10102 Google Scholar
[14]	Yokoyama T, Shinagawa H, Jin H 2014 J. Geophys. Res. Space Physics 119 10474
[15]	Yokoyama T 2017 Prog. in Earth and Planet. Sci. 4 37 Google Scholar
[16]	Krall J, Huba J D, Ossakow S L, Joyce G, Makela J J, Miller E S, Kelley M C 2011 Geophys. Res. Lett. 38 L08103
[17]	Krall J, Huba J D, Fritts D C 2013 Geophys. Res. Lett. 40 661 Google Scholar
[18]	Hines C O 1960 Can. J. Phys. 38 1441 Google Scholar
[19]	Alfonsi L, Spogli L, Pezzopane M, Romano V, Zuccheretti E, De Franceschi G, Cabrera M A, Ezquer R G 2013 J. Geophys. Res. Space Physics 118 4483 Google Scholar
[20]	Jiang C, Yang G, Deng C, Zhou C, Zhu P, Yokoyama T, Song H, Lan T, Ni B, Zhao Z, Zhang Y 2015 J. Geophys. Res. Space Physics 120 10979 Google Scholar
[21]	Jiang C, Yang G, Liu J, Zhao Z 2019 J. Geophys. Res. Space Physics 124 1317 Google Scholar
[22]	Sultan P J 1996 J. Geophys. Res. 101 26875 Google Scholar
[23]	Kelley M C 2009 Introduction to Spatial Econometrics (2nd ed.), (Amsterdams: Elsevier) p 99
[24]	Lanchester B S, Nygren T, Jarvis M J, Edwards R 1993 Ann. Geophys. 11 925
[25]	Miyoshi Y, Jin H, Fujiwara H, Shinagawa H 2018 J. Geophys. Res. Space Physics 123 2141
[26]	Abdu M A, Batista I S, Kantor I J, Sobral J H A 1982 J. Atmos. Terr. Phys. 44 759 Google Scholar
[27]	Fukumitsu K, Yabe T, Ogata Y, Oami T, Ohkubo T 2015 J. Comput. Phys. 286 62 Google Scholar
[28]	Yokoyama T, Jin H, Shinagawa H 2015 J. Geophys. Res. Space Physics 120 8810 Google Scholar

施引文献

图 1 水平东向电场值随高度的变化

Fig. 1. Altitudinal variation of eastward electrical field in the simulation.

下载: 全尺寸图片幻灯片

图 2 背景电离层电子密度剖面

Fig. 2. Electron density profile in the background ionos phere.

下载: 全尺寸图片幻灯片

图 3 存在TIDs(波长为300 km, 周期为40 min)扰动的背景电离层

Fig. 3. Background ionosphere with TIDs (horizontal wavelength is 300 km and period is 40 min).

下载: 全尺寸图片幻灯片

图 4 $\alpha = 1$时一维正弦扰动产生等离子体泡的发展过程

Fig. 4. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 1$.

下载: 全尺寸图片幻灯片

图 6 $\alpha = 0.01$时一维正弦扰动产生等离子体泡的发展过程

Fig. 6. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 0.01$.

下载: 全尺寸图片幻灯片

图 5 $\alpha = 0.1$时一维正弦扰动产生等离子体泡的发展过程

Fig. 5. Evolution of plasma bubbles caused by one dimensional disturbance with $\alpha = 0.1$.

下载: 全尺寸图片幻灯片

图 7 $\alpha = 1$时TIDs产生等离子体泡的发展过程

Fig. 7. Evolution of plasma bubbles caused by TIDs with $\alpha = 1$.

下载: 全尺寸图片幻灯片

图 8 $\alpha = 0.1$时TIDs产生等离子体泡的发展过程

Fig. 8. Evolution of plasma bubbles caused by TIDs with $\alpha = 0.1$.

下载: 全尺寸图片幻灯片

图 9 $\alpha = 0.01$时TIDs产生等离子体泡的发展过程

Fig. 9. Evolution of plasma bubbles caused by TIDs with $\alpha = 0.01$.

下载: 全尺寸图片幻灯片

图 10 $\alpha = 0$时TIDs产生等离子体泡的发展过程

Fig. 10. Evolution of plasma bubbles caused by TIDs with $\alpha = 0$.

下载: 全尺寸图片幻灯片

map

[1]	Dungey J W 1956 J. Atmos. Terr. Phys. 9 304 Google Scholar
[2]	Abdu M A 2001 J. Atmos. Terr. Phys. 63 869 Google Scholar
[3]	Tsunoda R T, Yamamoto M, Tsugawa T, Hoang T L, Ram S T, Thampi S V, Chau H D, Nagatsuma T 2011 Geophys. Res. Lett. 38 L20102 Google Scholar
[4]	Sekar R, Suhasini R, Raghavarao R 1994 J. Geophys. Res. 99 2205 Google Scholar
[5]	Huang C S, Kelley M C 1996 J. Geophys. Res. Space Physics 101 303 Google Scholar
[6]	Hysell D L, Kelley M C, Swartz W E, Woodman R F 1990 J. Geophys. Res. Space Physics 95 17253 Google Scholar
[7]	Huang C S, Kelley M C 1996 J. Geophys. Res. Space Physics 101 293 Google Scholar
[8]	Scannapieco A J, Ossakow S L 1976 Geophys. Res. Lett. 3 451 Google Scholar
[9]	Zalesak S T, Ossakow S L 1980 J. Geophys. Res. 85 2131 Google Scholar
[10]	Zalesak S T, Ossakow S L, Chaturvedi P K 1982 J. Geophys. Res. 87 151 Google Scholar
[11]	谢红, 肖佐 1993 地球 36 18 Google Scholar Xie H, Xiao Z 1993 Chinese J. Geophys. 36 18 Google Scholar
[12]	高泽, 方涵先, 汪四成, 杨升高 2017 地球 60 470 Google Scholar Gao Z, Fang H X, Wang S C, Yang S G 2017 Chinese J. Geophys. 60 470 Google Scholar
[13]	Huba J D, Joyce G, Krall J 2008 Geophys. Res. Lett. 35 10102 Google Scholar
[14]	Yokoyama T, Shinagawa H, Jin H 2014 J. Geophys. Res. Space Physics 119 10474
[15]	Yokoyama T 2017 Prog. in Earth and Planet. Sci. 4 37 Google Scholar
[16]	Krall J, Huba J D, Ossakow S L, Joyce G, Makela J J, Miller E S, Kelley M C 2011 Geophys. Res. Lett. 38 L08103
[17]	Krall J, Huba J D, Fritts D C 2013 Geophys. Res. Lett. 40 661 Google Scholar
[18]	Hines C O 1960 Can. J. Phys. 38 1441 Google Scholar
[19]	Alfonsi L, Spogli L, Pezzopane M, Romano V, Zuccheretti E, De Franceschi G, Cabrera M A, Ezquer R G 2013 J. Geophys. Res. Space Physics 118 4483 Google Scholar
[20]	Jiang C, Yang G, Deng C, Zhou C, Zhu P, Yokoyama T, Song H, Lan T, Ni B, Zhao Z, Zhang Y 2015 J. Geophys. Res. Space Physics 120 10979 Google Scholar
[21]	Jiang C, Yang G, Liu J, Zhao Z 2019 J. Geophys. Res. Space Physics 124 1317 Google Scholar
[22]	Sultan P J 1996 J. Geophys. Res. 101 26875 Google Scholar
[23]	Kelley M C 2009 Introduction to Spatial Econometrics (2nd ed.), (Amsterdams: Elsevier) p 99
[24]	Lanchester B S, Nygren T, Jarvis M J, Edwards R 1993 Ann. Geophys. 11 925
[25]	Miyoshi Y, Jin H, Fujiwara H, Shinagawa H 2018 J. Geophys. Res. Space Physics 123 2141
[26]	Abdu M A, Batista I S, Kantor I J, Sobral J H A 1982 J. Atmos. Terr. Phys. 44 759 Google Scholar
[27]	Fukumitsu K, Yabe T, Ogata Y, Oami T, Ohkubo T 2015 J. Comput. Phys. 286 62 Google Scholar
[28]	Yokoyama T, Jin H, Shinagawa H 2015 J. Geophys. Res. Space Physics 120 8810 Google Scholar

[1]	于博文, 何孝天, 徐进良. 超临界CO₂池式传热流固耦合传热特性数值模拟. , 2024, 73(10): 104401. doi: 10.7498/aps.73.20231953
[2]	牛越, 包为民, 李小平, 刘彦明, 刘东林. 大功率热平衡感应耦合等离子体数值模拟及实验研究. , 2021, 70(9): 095204. doi: 10.7498/aps.70.20201610
[3]	陈国华, 石科军, 储进科, 吴昊, 周池楼, 肖舒. 环形磁场金属等离子体源冷却流场的数值模拟与优化. , 2021, 70(7): 075203. doi: 10.7498/aps.70.20201368
[4]	丁明松, 江涛, 董维中, 高铁锁, 刘庆宗, 傅杨奥骁. 热化学模型对高超声速磁流体控制数值模拟影响分析. , 2019, 68(17): 174702. doi: 10.7498/aps.68.20190378
[5]	喻明浩. 非平衡感应耦合等离子体流场与电磁场作用机理的数值模拟. , 2019, 68(18): 185202. doi: 10.7498/aps.68.20190865
[6]	成玉国, 夏广庆. 感应式脉冲推力器中等离子体加速数值研究. , 2017, 66(7): 075204. doi: 10.7498/aps.66.075204
[7]	危卫, 张力元, 顾兆林. 工业中粉体颗粒的荷电机理及数值模拟方法. , 2015, 64(16): 168301. doi: 10.7498/aps.64.168301
[8]	蒋勇, 贺少勃, 袁晓东, 王海军, 廖威, 吕海兵, 刘春明, 向霞, 邱荣, 杨永佳, 郑万国, 祖小涛. CO2激光光栅式扫描修复熔石英表面缺陷的实验研究与数值模拟. , 2014, 63(6): 068105. doi: 10.7498/aps.63.068105
[9]	高启, 张传飞, 周林, 李正宏, 吴泽清, 雷雨, 章春来, 祖小涛. Z箍缩Al等离子体X特征辐射谱线数值模拟及考虑叠加效应后的修正. , 2014, 63(12): 125202. doi: 10.7498/aps.63.125202
[10]	靳冬欢, 刘文广, 陈星, 陆启生, 赵伊君. 三股互击式喷注器及燃烧室流场的数值模拟. , 2012, 61(6): 064206. doi: 10.7498/aps.61.064206
[11]	欧阳建明, 邵福球, 邹德滨. 大气等离子体中负氧离子产生和演化过程数值模拟. , 2011, 60(11): 110209. doi: 10.7498/aps.60.110209
[12]	庞学霞, 邓泽超, 贾鹏英, 梁伟华. 大气等离子体中氮氧化物粒子行为的数值模拟. , 2011, 60(12): 125201. doi: 10.7498/aps.60.125201
[13]	邓峰, 赵正予, 石润, 张援农. 中低纬电离层加热大尺度场向不均匀体的二维数值模拟. , 2009, 58(10): 7382-7391. doi: 10.7498/aps.58.7382
[14]	欧阳建明, 邵福球, 林明东. 含氧等离子体中臭氧形成过程数值模拟. , 2008, 57(5): 3293-3297. doi: 10.7498/aps.57.3293
[15]	庞学霞, 邓泽超, 董丽芳. 不同电离度下大气等离子体粒子行为的数值模拟. , 2008, 57(8): 5081-5088. doi: 10.7498/aps.57.5081
[16]	郭文琼, 周晓军, 张雄军, 隋展, 吴登生. 等离子体电极普克尔盒电光开关单脉冲过程数值模拟. , 2006, 55(7): 3519-3523. doi: 10.7498/aps.55.3519
[17]	欧阳建明, 邵福球, 王龙, 房同珍, 刘建全. 一维大气等离子体化学过程数值模拟. , 2006, 55(9): 4974-4979. doi: 10.7498/aps.55.4974
[18]	段耀勇, 郭永辉, 王文生, 邱爱慈. 钨丝阵等离子体Z箍缩的数值模拟. , 2004, 53(8): 2654-2660. doi: 10.7498/aps.53.2654
[19]	袁行球, 李　辉, 赵太泽, 王　飞, 郭文康, 须　平. 超音速等离子体炬的数值模拟. , 2004, 53(3): 788-792. doi: 10.7498/aps.53.788
[20]	于艳梅, 杨根仓, 赵达文, 吕衣礼, A. KARMA, C. BECKERMANN. 过冷熔体中枝晶生长的相场法数值模拟. , 2001, 50(12): 2423-2428. doi: 10.7498/aps.50.2423

计量

文章访问数: 8235
PDF下载量: 67
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

化学复合率对激发赤道等离子体泡影响的数值模拟