分子动力学中的几何相位

杨欢; 郑雨军

doi:10.7498/aps.74.20250388

摘要

分子的几何相位效应, 也称为分子Aharonov-Bohm效应, 源于对势能面锥形交叉结构的研究. 在核构型空间环绕锥形交叉点时, 绝热的电子波函数会获得π的相位, 导致其符号反转; 而核的波函数也需相应地改变符号, 保持总波函数的单值性. 该相位与锥形交叉结构拓扑相关, 只有适当地引入分子几何相位才能在绝热表象下准确地描述量子体系的动力学行为. 在透热表象下, 可以隐式地处理几何相位效应以及核-电子的非绝热耦合问题. 本文基于几何相位的量子动力学方法, 设计了一种可以直接提取分子动力学中几何相位的方法. 该相位不同于由锥形交叉拓扑结构导致的量子化的π相位, 它是连续变化的, 是量子体系在投影希尔伯特空间演化时, 几何相位的一种规范不变的表示. 本文的研究为探索分子几何相位及其效应开辟了一个新视角, 并有望为实验研究分子动力学中的几何相位提供一个可能的观测量.

关键词:

Abstract

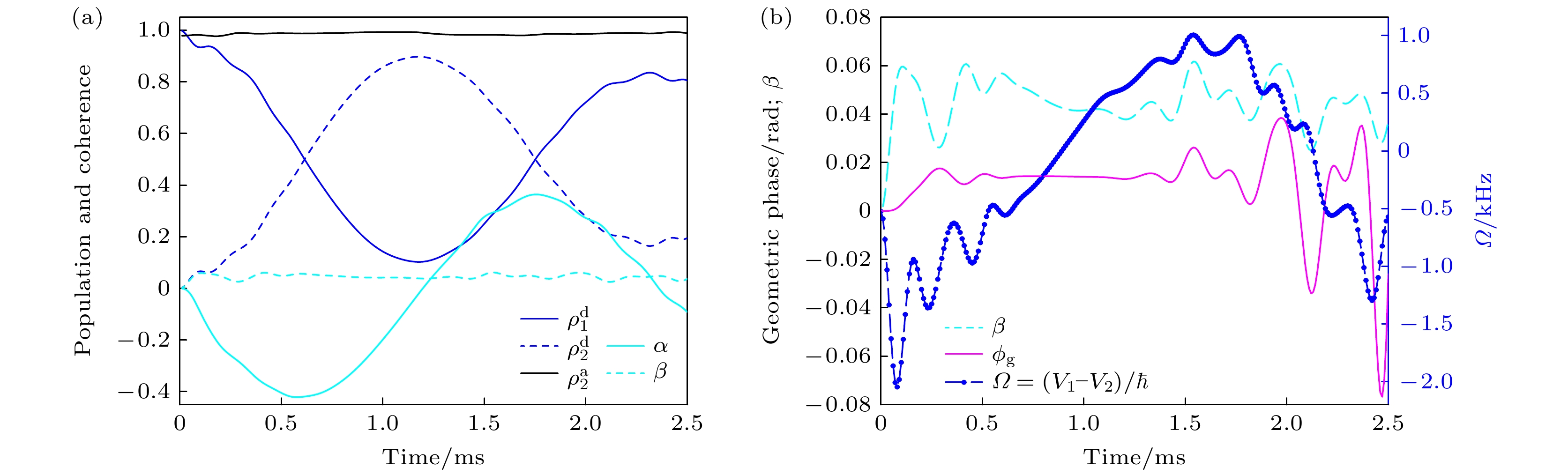
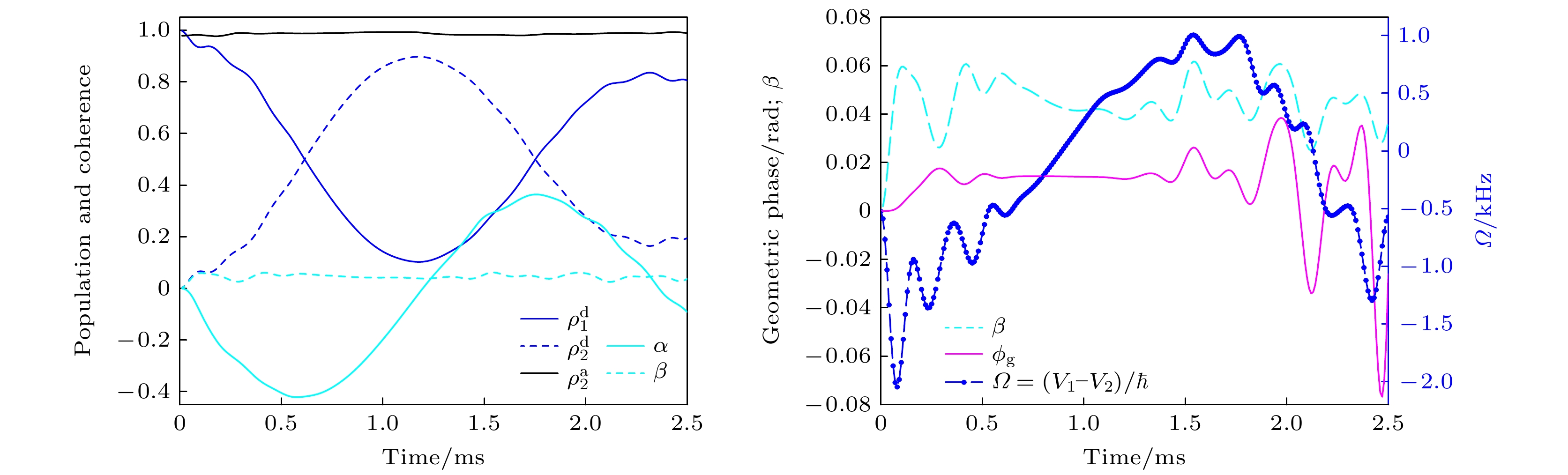
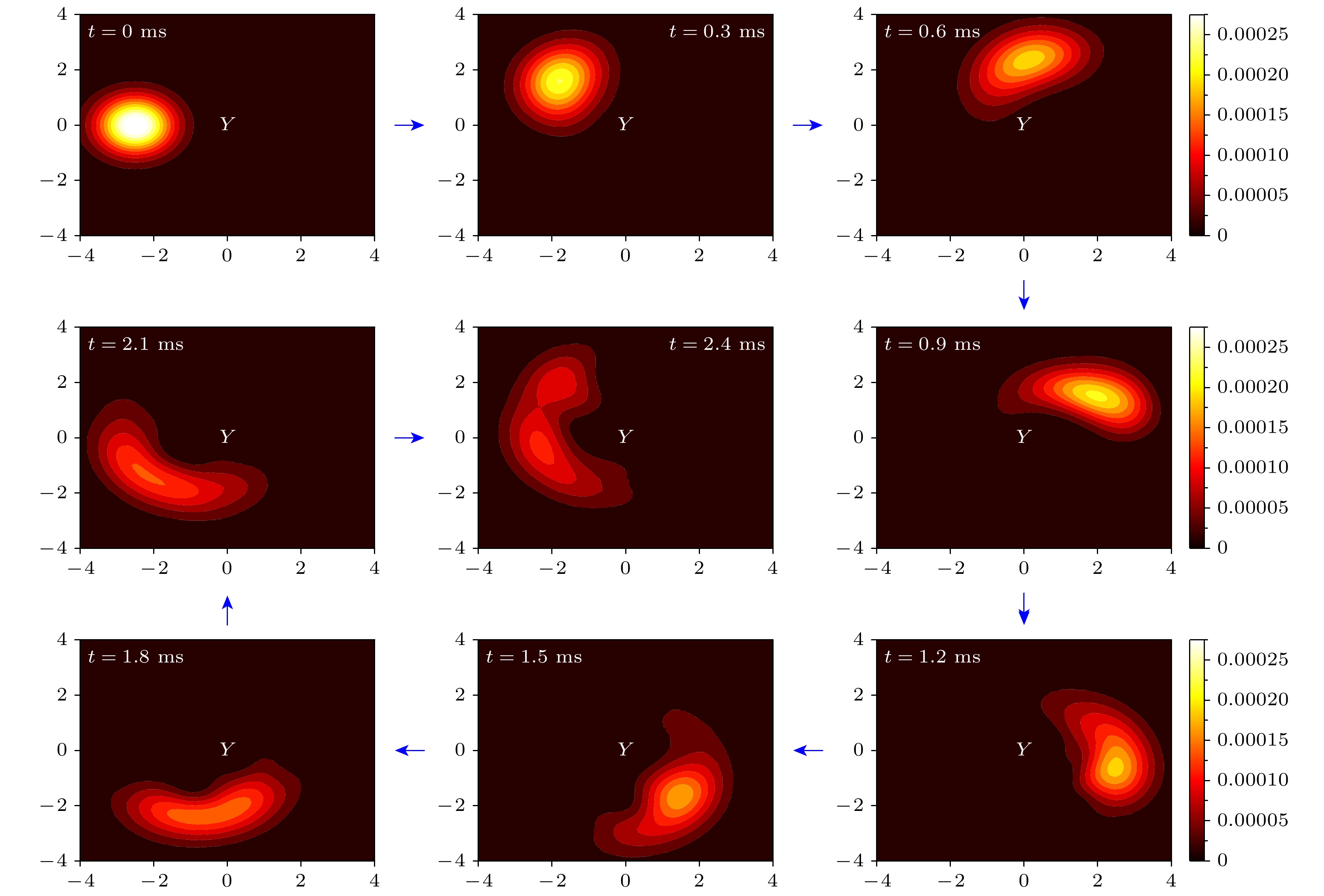
The geometric phase effect of molecules, also known as the molecular Aharonov-Bohm effect, arises from the study of the conical intersections of potential energy surfaces. When encircling a conical intersection in the nuclear configuration space, the adiabatic electronic wave function acquires a π phase, leading to a change in sign. Consequently, the nuclear wave function must also change its sign to maintain the single-valued nature of the total wave function. This phase is topologically related to the conical intersection structure. Only by appropriately introducing the molecular geometric phase can the quantum dynamical behavior in the adiabatic representation be accurately described. In the diabatic representation, both the geometric phase effects and the non-adiabatic couplings between nuclei and electrons can be implicitly handled.In this paper, according to the quantum kinematic approach to the geometric phase, we propose a method for directly extracting the geometric phase in molecular dynamics. To demonstrate the unique features of this method, we adopt the $E \otimes e $ Jahn-Teller model, which is a standard model that includes a cone intersection point. This model comprises two diabatic electronic states coupled with two vibrational modes. The initial wave function is designed in such a way that it can circumnavigate the conical intersection in an almost adiabatic manner within approximately 2.4 ms. Subsequently, the quantum kinematic approach is utilized to extract the geometric phase during the evolution. In contrast to the typical topological effect of a quantized geometric phase of π, this extracted geometric phase in this case varies in a continuous manner. When a quantum system performs a path in its projected Hilbert space, it is a representation-independent and gauge-invariant formula of the geometric phase. This research provides a new perspective for exploring molecular geometric phases and the geometric phase effects. It may also provide a possible observable for experimentally studying geometric phases in molecular dynamics.

Keywords:

作者及机构信息

杨欢,
郑雨军

山东大学物理学院, 济南　250100

通信作者: 郑雨军, yzheng@sdu.edu.cn

基金项目: 国家自然科学基金重点项目 (批准号: 12234013) 和国家自然科学基金 (批准号: 12374268) 资助的课题.

Authors and contacts

School of Physics, Shandong University, Jinan 250100, China

Corresponding author: ZHENG Yujun, yzheng@sdu.edu.cn

Funds: Project supported by the Key Program of the National Natural Science Foundation of China (Grant No. 12234013) and the National Natural Science Foundation of China (Grant No. 12374268).

文章全文

参考文献

[1]	Pancharatnam S 1956 Proc. Indian Acad. Sci. A 44 247 Google Scholar
[2]	Berry M V 1984 Proc. R. Soc. London, Ser. A 392 45 Google Scholar
[3]	Simon B 1983 Phys. Rev. Lett. 51 2167 Google Scholar
[4]	Aharonov Y, Anandan J 1987 Phys. Rev. Lett. 58 1593 Google Scholar
[5]	Samuel J, Bhandari R 1988 Phys. Rev. Lett. 60 2339 Google Scholar
[6]	Garrison J C, Wright E M 1988 Phys. Lett. A 128 177 Google Scholar
[7]	Cui X D, Zheng Y 2012 Phys. Rev. A 86 247 Google Scholar
[8]	Cui X D, Zheng Y 2014 Sci. Rep. 4 5813 Google Scholar
[9]	Cui X D, Zheng Y 2015 J. Chem. Phys. 142 214311 Google Scholar
[10]	Zhou Y, Wu Z H, Ge M L 1999 Chin. Phys. Lett. 16 316 Google Scholar
[11]	Wang L C, Yan J Y, Yi X X 2010 Chin. Phys. B 19 040512 Google Scholar
[12]	饶黄云, 刘义保, 江燕燕, 郭立平, 王资生 2012 61 020302 Google Scholar Rao H Y, Liu Y B, Jiang Y Y, Guo L P, Wang Z S 2012 Acta Phys. Sin. 61 020302 Google Scholar
[13]	王子, 任捷 2021 70 230503 Google Scholar Wang Z, Ren J 2021 Acta Phys. Sin. 70 230503 Google Scholar
[14]	孙舒宁, 郑雨军 2021 科学通报 66 1946 Google Scholar Sun S N, Zheng Y J 2021 Chin. Sci. Bull. 66 1946 Google Scholar
[15]	Liu W, Wang T, Li W 2023 Chin. Phys. B 32 050311 Google Scholar
[16]	Herzberg G, Longuet-Higgins H C 1963 Discuss. Faraday Soc. 35 77 Google Scholar
[17]	Requist R, Tandetzky F, Gross E K U 2016 Phys. Rev. A 93 042108 Google Scholar
[18]	Mead C A 1980 Chem. Phys. 49 23 Google Scholar
[19]	Juanes-Marcos J C, Althorpe S C, Wrede E 2005 Science 309 1227 Google Scholar
[20]	Kendrick B K, Hazra J, Balakrishnan N 2015 Nat. Commun. 6 7918 Google Scholar
[21]	Wang J, Xie C, Hu X, Guo H, Xie D 2024 J. Phys. Chem. Lett. 4237 Google Scholar
[22]	Li S, Huang J, Lu Z, Shu Y, Chen W, Yuan D, Wang T, Fu B, Zhang Z, Wang X, Zhang D H, Yang X 2024 Nat. Commun. 15 1698 Google Scholar
[23]	Xie C, Ma J, Zhu X, Yarkony D R, Xie D, Guo H 2016 J. Am. Chem. Soc. 138 7828 Google Scholar
[24]	Kendrick B 1997 Phys. Rev. Lett. 79 2431 Google Scholar
[25]	Babikov D, Kendrick B K, Zhang P, Morokuma K 2005 J. Chem. Phys. 122 044315 Google Scholar
[26]	Mead C A, Truhlar D G 1979 J. Chem. Phys. 70 2284 Google Scholar
[27]	Kendrick B, Mead C A 1995 J. Chem. Phys. 102 4160 Google Scholar
[28]	Aharonov Y, Bohm D 1959 Phys. Rev. 115 485 Google Scholar
[29]	Xie C, Malbon C L, Yarkony D R, Guo H 2017 J. Chem. Phys. 147 044109 Google Scholar
[30]	Yuan D, Guan Y, Chen W, Zhao H, Yu S, Luo C, Tan Y, Xie T, Wang X, Sun Z, Zhang D H, Yang X 2018 Science 362 1289 Google Scholar
[31]	He H, Xu H, Chen L, Xie P, Yin S 2023 J. Phys. Chem. A 127 9966 Google Scholar
[32]	Min S K, Abedi A, Kim K S, Gross E K U 2014 Phys. Rev. Lett. 113 263004 Google Scholar
[33]	Ibele L M, Sangiogo Gil E, Curchod B F E, Agostini F 2023 J. Phys. Chem. Lett. 14 11625 Google Scholar
[34]	Li Y, Wang Z, Li C 2024 J. Phys. Condens. Matter 36 465201 Google Scholar
[35]	Martinazzo R, Burghardt I 2024 Phys. Rev. Lett. 132 243002 Google Scholar
[36]	Leek P J, Fink J M, Blais A, Bianchetti R, Göppl M, Gambetta J M, Schuster D I, Frunzio L, Schoelkopf R J, Wallraff A 2007 Science 318 1889 Google Scholar
[37]	Zhou H, Li Z K, Wang H Y, Chen H W, Peng X H, Du J F 2016 Chin. Phys. Lett. 33 060301 Google Scholar
[38]	Arai K, Lee J, Belthangady C, Glenn D R, Zhang H, Walsworth R L 2018 Nat. Commun. 9 4996 Google Scholar
[39]	宋睿睿, 邓钦玲, 周绍林 2022 71 029101 Google Scholar Song R R, Deng Q L, Zhou S L 2022 Acta Phys. Sin. 71 029101 Google Scholar
[40]	Mukunda N, Simon R 1993 Ann. Phys. 228 205 Google Scholar
[41]	Yang H, Zheng Y 2024 J. Phys. Chem. A 128 9519 Google Scholar
[42]	Longuet-Higgins H C, Öpik U, Pryce M H L, Sack R A 1958 Proc. R. Soc. London, Ser. A 244 1 Google Scholar
[43]	Schön J, Köppel H 1995 J. Chem. Phys. 103 9292 Google Scholar
[44]	Requist R, Proetto C R, Gross E K U 2017 Phys. Rev. A 96 062503 Google Scholar
[45]	Ribeiro R F, Joel Y Z 2018 J. Phys. Chem. Lett. 9 242 Google Scholar
[46]	Valahu C H, Olaya-Agudelo V C, MacDonell R J, Navickas T, Rao A D, Millican M J, Pérez-Sánchez J B, Yuen-Zhou J, Biercuk M J, Hempel C, Tan T R, Kassal I 2023 Nat. Chem. 15 1503 Google Scholar
[47]	Martinazzo R, Burghardt I 2024 J. Phys. Chem. Lett. 15 10416 Google Scholar
[48]	Martens C C 2016 J. Phys. Chem. Lett. 7 2610 Google Scholar

施引文献

图 1 核波函数总的概率密度随时间的演化

Fig. 1. Evolution of total nuclear density versus time.

下载: 全尺寸图片幻灯片

图 2 布居、相干(a)以及几何相位(b)随时间的演化

Fig. 2. Evolution of population, coherence (a) and geometric phase (b) versus time.

下载: 全尺寸图片幻灯片

map

[1]	Pancharatnam S 1956 Proc. Indian Acad. Sci. A 44 247 Google Scholar
[2]	Berry M V 1984 Proc. R. Soc. London, Ser. A 392 45 Google Scholar
[3]	Simon B 1983 Phys. Rev. Lett. 51 2167 Google Scholar
[4]	Aharonov Y, Anandan J 1987 Phys. Rev. Lett. 58 1593 Google Scholar
[5]	Samuel J, Bhandari R 1988 Phys. Rev. Lett. 60 2339 Google Scholar
[6]	Garrison J C, Wright E M 1988 Phys. Lett. A 128 177 Google Scholar
[7]	Cui X D, Zheng Y 2012 Phys. Rev. A 86 247 Google Scholar
[8]	Cui X D, Zheng Y 2014 Sci. Rep. 4 5813 Google Scholar
[9]	Cui X D, Zheng Y 2015 J. Chem. Phys. 142 214311 Google Scholar
[10]	Zhou Y, Wu Z H, Ge M L 1999 Chin. Phys. Lett. 16 316 Google Scholar
[11]	Wang L C, Yan J Y, Yi X X 2010 Chin. Phys. B 19 040512 Google Scholar
[12]	饶黄云, 刘义保, 江燕燕, 郭立平, 王资生 2012 61 020302 Google Scholar Rao H Y, Liu Y B, Jiang Y Y, Guo L P, Wang Z S 2012 Acta Phys. Sin. 61 020302 Google Scholar
[13]	王子, 任捷 2021 70 230503 Google Scholar Wang Z, Ren J 2021 Acta Phys. Sin. 70 230503 Google Scholar
[14]	孙舒宁, 郑雨军 2021 科学通报 66 1946 Google Scholar Sun S N, Zheng Y J 2021 Chin. Sci. Bull. 66 1946 Google Scholar
[15]	Liu W, Wang T, Li W 2023 Chin. Phys. B 32 050311 Google Scholar
[16]	Herzberg G, Longuet-Higgins H C 1963 Discuss. Faraday Soc. 35 77 Google Scholar
[17]	Requist R, Tandetzky F, Gross E K U 2016 Phys. Rev. A 93 042108 Google Scholar
[18]	Mead C A 1980 Chem. Phys. 49 23 Google Scholar
[19]	Juanes-Marcos J C, Althorpe S C, Wrede E 2005 Science 309 1227 Google Scholar
[20]	Kendrick B K, Hazra J, Balakrishnan N 2015 Nat. Commun. 6 7918 Google Scholar
[21]	Wang J, Xie C, Hu X, Guo H, Xie D 2024 J. Phys. Chem. Lett. 4237 Google Scholar
[22]	Li S, Huang J, Lu Z, Shu Y, Chen W, Yuan D, Wang T, Fu B, Zhang Z, Wang X, Zhang D H, Yang X 2024 Nat. Commun. 15 1698 Google Scholar
[23]	Xie C, Ma J, Zhu X, Yarkony D R, Xie D, Guo H 2016 J. Am. Chem. Soc. 138 7828 Google Scholar
[24]	Kendrick B 1997 Phys. Rev. Lett. 79 2431 Google Scholar
[25]	Babikov D, Kendrick B K, Zhang P, Morokuma K 2005 J. Chem. Phys. 122 044315 Google Scholar
[26]	Mead C A, Truhlar D G 1979 J. Chem. Phys. 70 2284 Google Scholar
[27]	Kendrick B, Mead C A 1995 J. Chem. Phys. 102 4160 Google Scholar
[28]	Aharonov Y, Bohm D 1959 Phys. Rev. 115 485 Google Scholar
[29]	Xie C, Malbon C L, Yarkony D R, Guo H 2017 J. Chem. Phys. 147 044109 Google Scholar
[30]	Yuan D, Guan Y, Chen W, Zhao H, Yu S, Luo C, Tan Y, Xie T, Wang X, Sun Z, Zhang D H, Yang X 2018 Science 362 1289 Google Scholar
[31]	He H, Xu H, Chen L, Xie P, Yin S 2023 J. Phys. Chem. A 127 9966 Google Scholar
[32]	Min S K, Abedi A, Kim K S, Gross E K U 2014 Phys. Rev. Lett. 113 263004 Google Scholar
[33]	Ibele L M, Sangiogo Gil E, Curchod B F E, Agostini F 2023 J. Phys. Chem. Lett. 14 11625 Google Scholar
[34]	Li Y, Wang Z, Li C 2024 J. Phys. Condens. Matter 36 465201 Google Scholar
[35]	Martinazzo R, Burghardt I 2024 Phys. Rev. Lett. 132 243002 Google Scholar
[36]	Leek P J, Fink J M, Blais A, Bianchetti R, Göppl M, Gambetta J M, Schuster D I, Frunzio L, Schoelkopf R J, Wallraff A 2007 Science 318 1889 Google Scholar
[37]	Zhou H, Li Z K, Wang H Y, Chen H W, Peng X H, Du J F 2016 Chin. Phys. Lett. 33 060301 Google Scholar
[38]	Arai K, Lee J, Belthangady C, Glenn D R, Zhang H, Walsworth R L 2018 Nat. Commun. 9 4996 Google Scholar
[39]	宋睿睿, 邓钦玲, 周绍林 2022 71 029101 Google Scholar Song R R, Deng Q L, Zhou S L 2022 Acta Phys. Sin. 71 029101 Google Scholar
[40]	Mukunda N, Simon R 1993 Ann. Phys. 228 205 Google Scholar
[41]	Yang H, Zheng Y 2024 J. Phys. Chem. A 128 9519 Google Scholar
[42]	Longuet-Higgins H C, Öpik U, Pryce M H L, Sack R A 1958 Proc. R. Soc. London, Ser. A 244 1 Google Scholar
[43]	Schön J, Köppel H 1995 J. Chem. Phys. 103 9292 Google Scholar
[44]	Requist R, Proetto C R, Gross E K U 2017 Phys. Rev. A 96 062503 Google Scholar
[45]	Ribeiro R F, Joel Y Z 2018 J. Phys. Chem. Lett. 9 242 Google Scholar
[46]	Valahu C H, Olaya-Agudelo V C, MacDonell R J, Navickas T, Rao A D, Millican M J, Pérez-Sánchez J B, Yuen-Zhou J, Biercuk M J, Hempel C, Tan T R, Kassal I 2023 Nat. Chem. 15 1503 Google Scholar
[47]	Martinazzo R, Burghardt I 2024 J. Phys. Chem. Lett. 15 10416 Google Scholar
[48]	Martens C C 2016 J. Phys. Chem. Lett. 7 2610 Google Scholar

计量

文章访问数: 4561
PDF下载量: 107
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

分子动力学中的几何相位