-
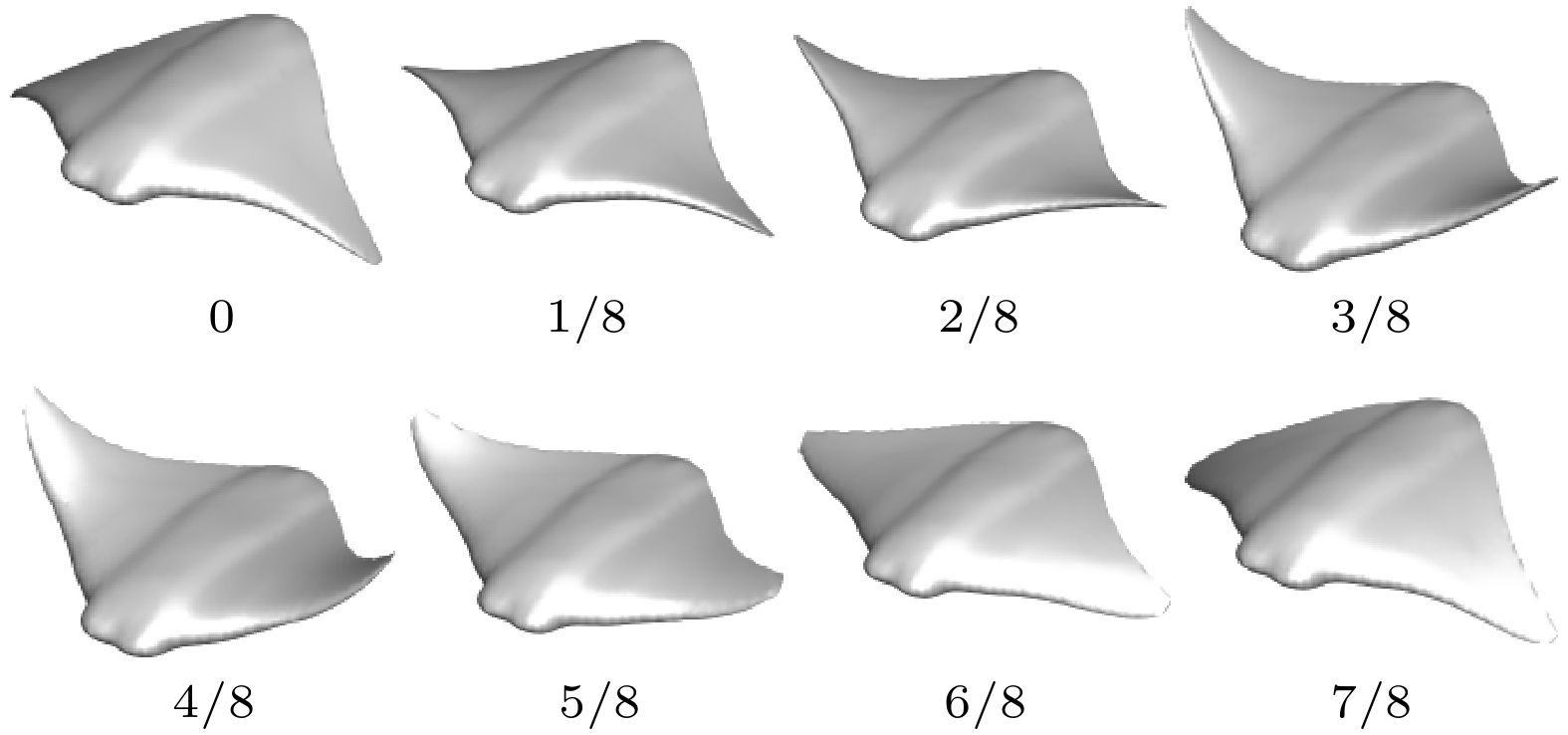
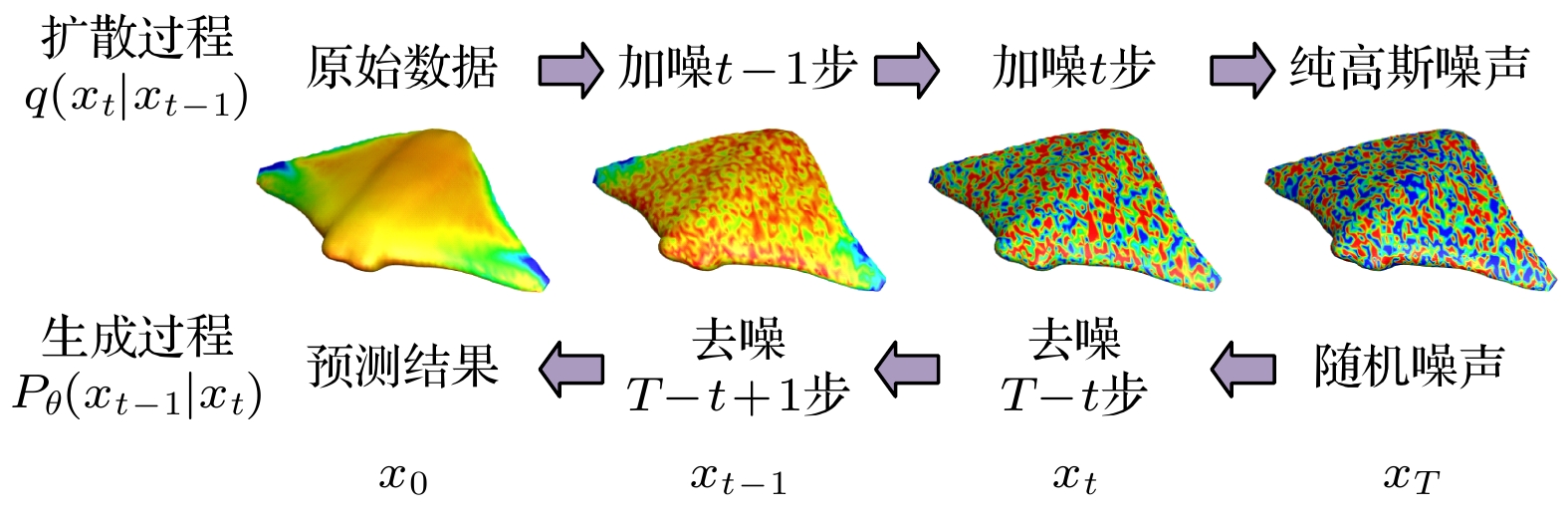
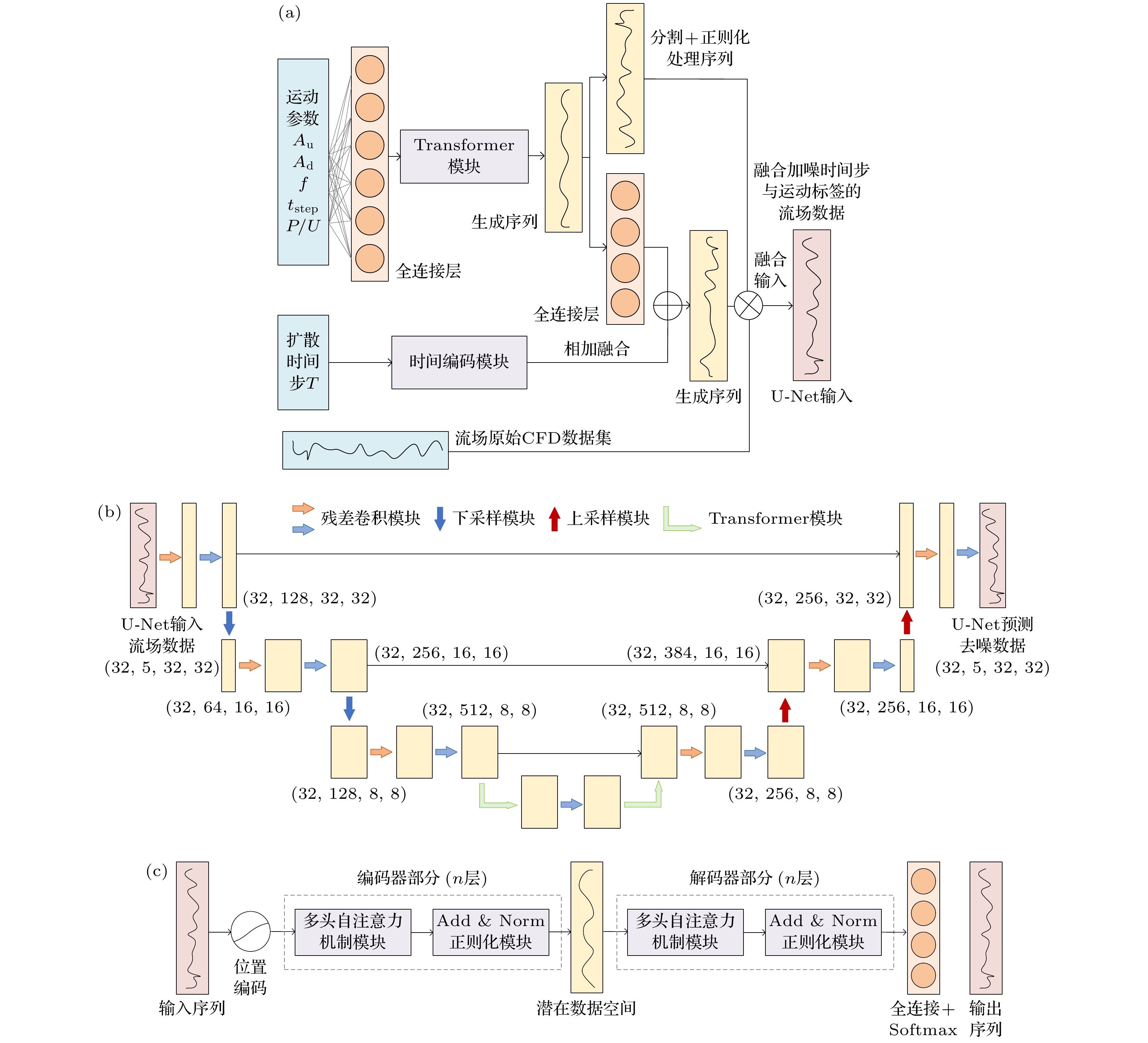
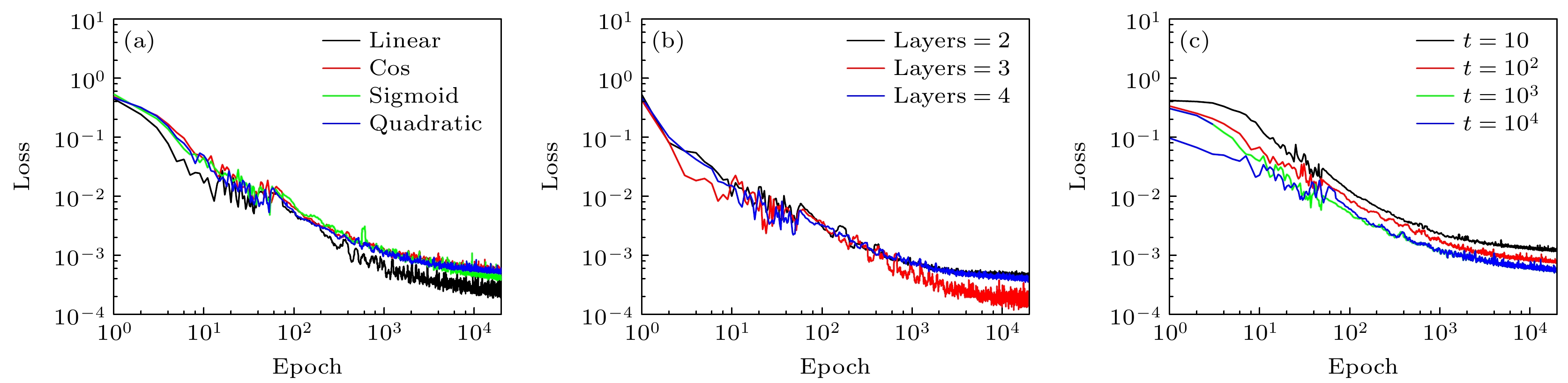
为解决传统数值模拟方法在蝠鲼三维柔性大变形流场仿真中计算资源与时间上的局限性, 本文提出一种基于去噪概率扩散模型的生成式人工智能方法(surf-DDPM), 通过输入运动参数变量组, 预测蝠鲼表面流场. 首先, 采用浸入边界法和球函数气体动理学格式(IB-SGKS)建立蝠鲼扑动模态的数值计算方法, 获取了在0.3—0.9 Hz频率和0.1—0.6倍体长幅值条件下共180组非定常流场数据集. 其次, 构建了噪声扩散过程的马尔科夫链和去噪生成过程的神经网络模型, 并将运动参数与扩散时间步标签嵌入网络, 完成模型训练. 最后, 验证了神经网络超参数对模型预测的影响, 并可视化了未参与训练的多扑动姿态压力场和速度场预测结果, 进行预报结果准确性、不确定度与预测效率量化分析. 结果显示, 该模型实现了具有大跨度高维上采样特征的蝠鲼表面流场数据的快速准确预测, 预报结果全部位于95%置信区间内, 单工况预测相较CFD方法效率提升99.97%.The manta ray is a large marine species, which has the ability of gliding efficiently and flapping rapidly. It can autonomously switch between various motion modes, such as gliding, flapping, and group swimming, based on ocean currents and seabed conditions. To address the computational resource and time constraints of traditional numerical simulation methods in modeling the manta ray’s three-dimensional (3D) large-deformation flow field, this study proposes a novel generative artificial intelligence approach based on a denoising probabilistic diffusion model (surf-DDPM). This method predicts the surface flow field of the manta ray by inputting a set of motion parameter variables. Initially, we establish a numerical simulation method for the manta ray’s flapping mode by using the immersed boundary method and the spherical function gas kinetic scheme (IB-SGKS), generating an unsteady flow dataset comprising 180 sets under frequency conditions of 0.3–0.9 Hz and amplitude conditions of 0.1–0.6 body lengths. Data augmentation is then performed. Subsequently, a Markov chain for the noise diffusion process and a neural network model for the denoising generation process are constructed. A pretrained neural network embeds the motion parameters and diffusion time step labels into the flow field data, which are then fed into a U-Net for model training. Notably, a transformer network is incorporated into the U-Net architecture to enable the handling of long-sequence data. Finally, we examine the influence of neural network hyperparameters on model performance and visualize the predicted pressure and velocity fields for multi-flapping postures that were not included in the training set, followed by a quantitative analysis of prediction accuracy, uncertainty, and efficiency. The results demonstrate that the proposed model achieves fast and accurate predictions of the manta ray’s surface flow field, characterized by extensive high-dimensional upsampling. The minimum PSNR value and SSIM value of the predictions are 35.931 dB and 0.9524, respectively, with all data falling within the 95% prediction interval. Compared with CFD simulations, the single-condition simulations by using AI model show that the prediction efficiency is enhanced by 99.97%.
-
Keywords:
- manta rays /
- fluid mechanics /
- artificial intelligence /
- flow field prediction
[1] 王亮 2007 博士学位论文 (南京: 河海大学)
Wang L 2007 Ph. D. Dissertation (Nanjing: Hehai University
[2] Asada T, Furuhashi H 2024 Ocean Eng. 308 118261
 Google Scholar
Google Scholar
[3] Xing C, Yin Z, Xu H, Cao Y, Qu Y, Huang Q 2024 Ocean Eng. 312 119039
 Google Scholar
Google Scholar
[4] Bao T, Cao Y, Cao Y H, Lu Y, Pan G, Huang Q G 2024 Ocean Eng. 309 118377
 Google Scholar
Google Scholar
[5] Dong H, Bozkurttas M, Mittal R, Madden P, Laude G V 2010 J. Fluid Mech. 645 34
 Google Scholar
Google Scholar
[6] Huang Z, Menzer A, Guo J, Dong H 2024 Bioinspir Biomim 19 026004
 Google Scholar
Google Scholar
[7] Wang S, Gao P, Huang Q G, Pan G, Tian X 2024 Ocean Eng. 294 116799
 Google Scholar
Google Scholar
[8] Gao P C, Song B, Huang Q G, Tian X S, Pan G, Chu Y, Bai J Y 2024 Ocean Eng. 313 119415
 Google Scholar
Google Scholar
[9] Gao P C, Huang Q G, Pan G, Cao Y, Luo Y 2023 Ocean Eng. 278 114389
 Google Scholar
Google Scholar
[10] Miyanawala T P, Li Y, Law Y Z 2024 Ocean Eng. 306 118003
 Google Scholar
Google Scholar
[11] Li G, Zhu H, Jian H 2023 J. Hydrol. 625 130025
 Google Scholar
Google Scholar
[12] 战庆亮, 葛耀君, 白春锦 2022 71 074701
 Google Scholar
Google Scholar
Zhan Q L, Ge Y J, Bai C J 2022 Acta Phys. Sin. 71 074701
 Google Scholar
Google Scholar
[13] Wang Z, Zhang W 2023 Phys. Fluids 35 025124
 Google Scholar
Google Scholar
[14] Qiu C C, Huang Q G, Pan G 2023 Phys. Fluids 35 017132
 Google Scholar
Google Scholar
[15] Xia Y, Li T, Wang Q, Yue J, Peng B, Yi X 2024 Phys. Fluids 36 103313
 Google Scholar
Google Scholar
[16] Li R, Song B, Chen Y 2024 Ocean Eng. 304 117857
 Google Scholar
Google Scholar
[17] Caraccio P, Marseglia G, Lauria A 2024 Phys. Fluids 36 107120
 Google Scholar
Google Scholar
[18] Qiu C C, Huang Q G, Pan G 2023 Ocean Eng. 281 114555
 Google Scholar
Google Scholar
[19] Gao H, Gao L, Shi Z, Sun D, Sun X 2024 Aerosp. Sci. Technol. 147 108977
 Google Scholar
Google Scholar
[20] Lin H, Jiang X, Deng X 2024 Thinking Skills and Creativity 54 101649
 Google Scholar
Google Scholar
[21] Kartashov N, Vlassis N N 2024 arXiv: 2409.14473 [cs.CE]
[22] Torem N, Ronen R, Schechner Y Y, Elad M 2023 Proceedings of the IEEE/CVF International Conference on Computer Vision Paris, France, October 2–6, 2023 p3810
[23] Ho J, Jain A, Abbeel P 2020 Adv. Neural Inf. Process. Syst. 33 6840
 Google Scholar
Google Scholar
[24] Rombach R, Blattmann A, Loren D, Esser P, Ommer B 2022 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition New Orleans, LA, June 18–24, 2022 p10674
[25] Song J, Meng C, Ermon S 2020 arXiv: 2010.02502 [cs.LG]
[26] Nichol A, Dhariwal P, Ramesh A, Shyam P, Mishkin P, McGrew B 2021 arXiv: 2112.10741 [cs.CV]
[27] Huang L, Zheng C, Chen Y 2024 Phys. Fluids 36 095113
 Google Scholar
Google Scholar
[28] Rybchuk A, Hassanaly M, Hamilton N 2023 Phys. Fluids 35 126604
 Google Scholar
Google Scholar
[29] Gao P C, Tian X, Huang Q G 2024 Phys. Fluids 36 011902
 Google Scholar
Google Scholar
[30] Gao P C, Huang Q G, Pan G 2023 Phys. Fluids 35 061909
 Google Scholar
Google Scholar
[31] 张栋 2020 博士学位论文 (西安: 西北工业大学)
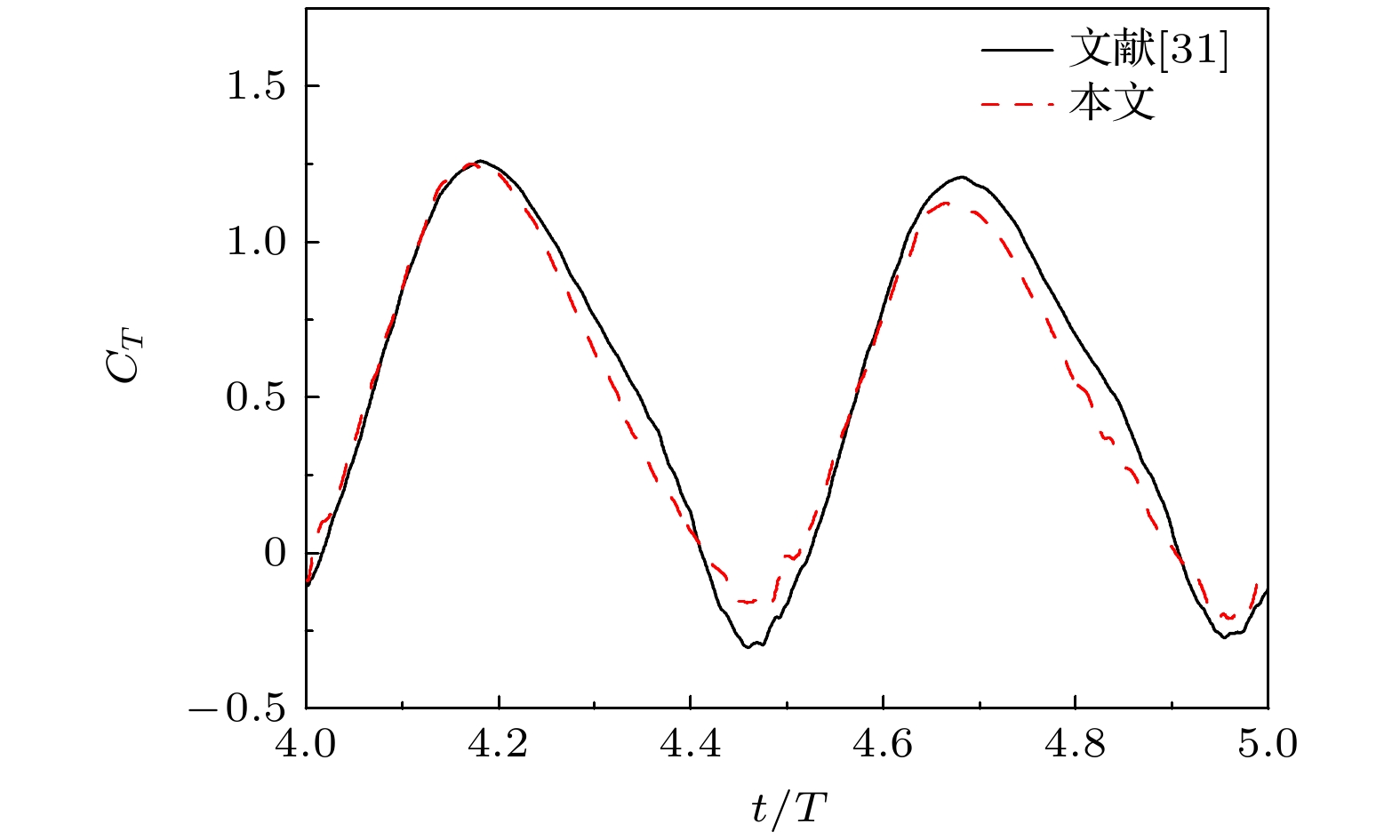
Zhang D 2020 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University
-
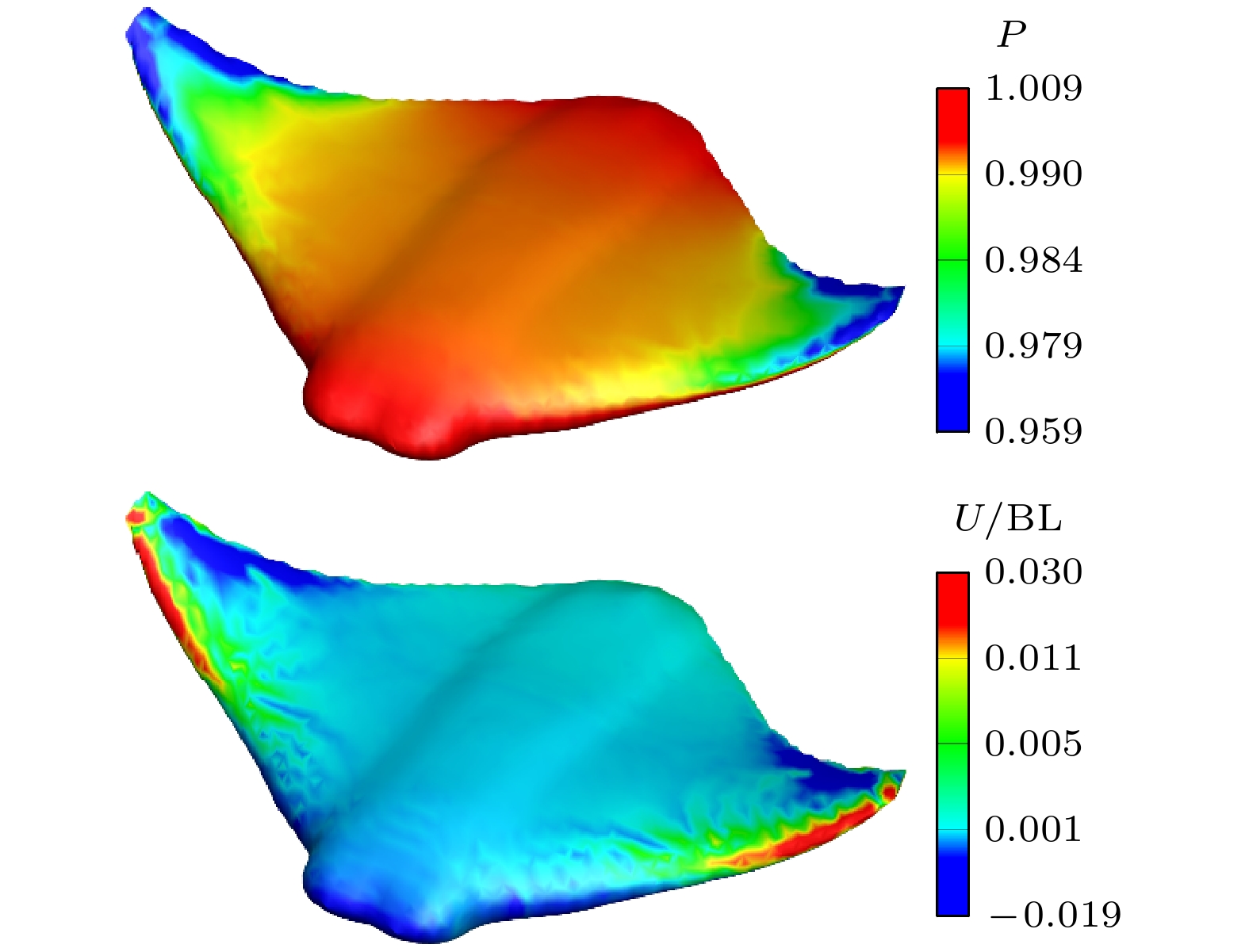
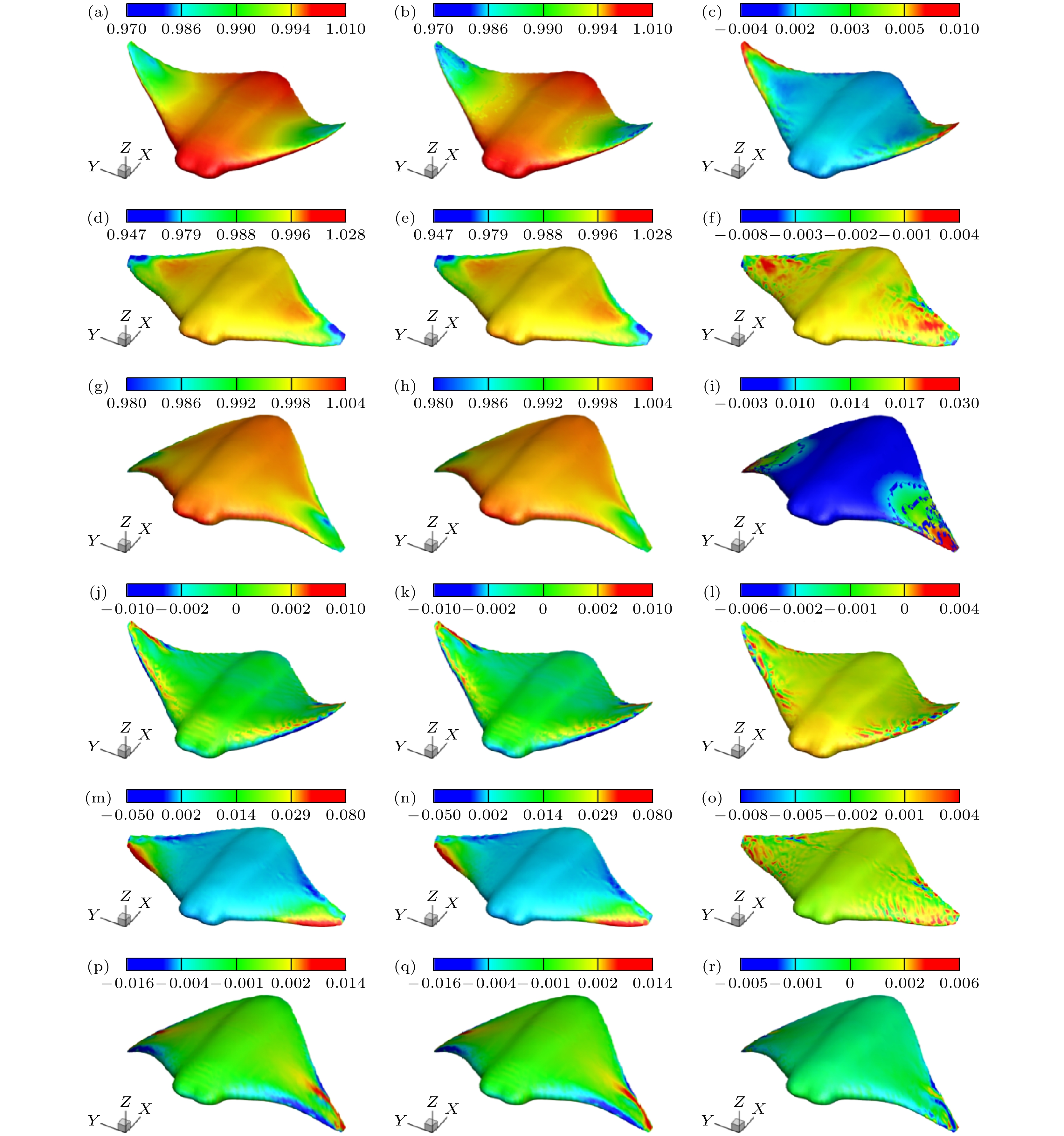
图 10 内插测试工况压力与速度场预测结果与误差 (a), (d), (g)压力场CFD计算真值; (b), (e), (h) surf-DDPM人工智能模型预测结果; (c), (f), (i)预测值误差云图; (j), (m), (p)速度场CFD计算真值; (k), (n), (q) surf-DDPM人工智能模型预测结果; (l), (o), (r)预测值误差云图
Fig. 10. Predicted results and errors of surface pressure and velocity fields for the interpolation test case: (a), (d), (g) True values of dynamic pressure field from CFD simulations; (b), (e), (h) pressure field predicted by surf-DDPM AI model; (c), (f), (i) absolute error contour of pressure field; (j), (m), (p) true values of velocity flow field from CFD simulations; (k), (n), (q) velocity field predicted by surf-DDPM AI model; (l), (o), (r) absolute error contour of velocity field.
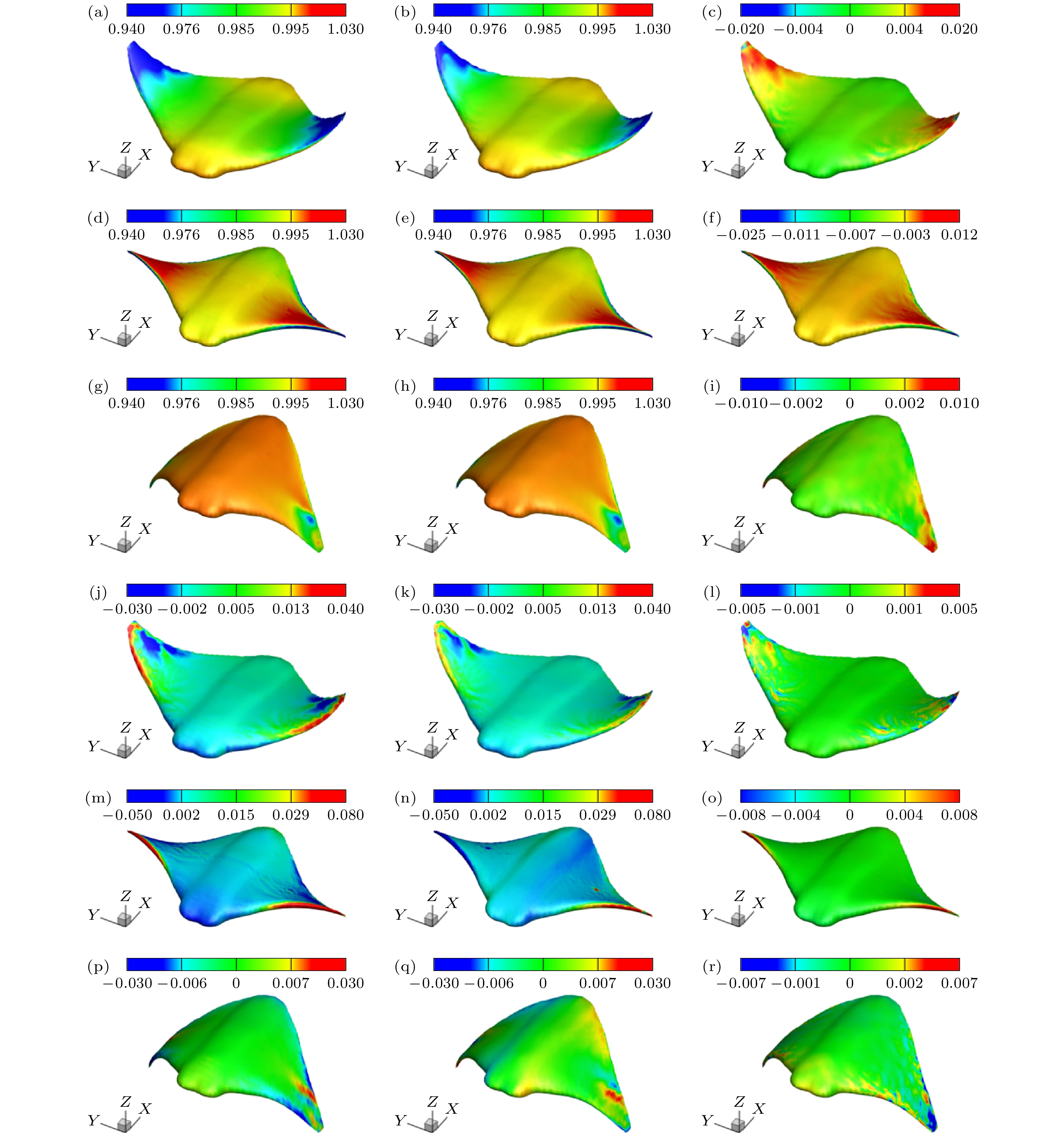
图 11 外推测试工况压力场与速度场预测结果与误差 (a), (d), (g)压力场CFD计算真值; (b), (e), (h) surf-DDPM人工智能模型预测结果; (c), (f), (i)预测值误差云图; (j), (m), (p)速度场CFD计算真值; (k), (n), (q) surf-DDPM人工智能模型预测结果; (l), (o), (r)预测值误差云图
Fig. 11. Prediction results and errors of pressure and velocity fields in extrapolation test cases: (a), (d), (g) True values ofdynamic pressure field from CFD simulations; (b), (e), (h) pressure field predicted by surf-DDPM AI model; (c), (f), (i) absoluteer-ror contour of pressure field; (j), (m), (p) true values of velocity flow field from CFD simulations; (k), (n), (q) velocity fieldpre-dicted by surf-DDPM AI model; (l), (o), (r) absolute error contour of velocity field.
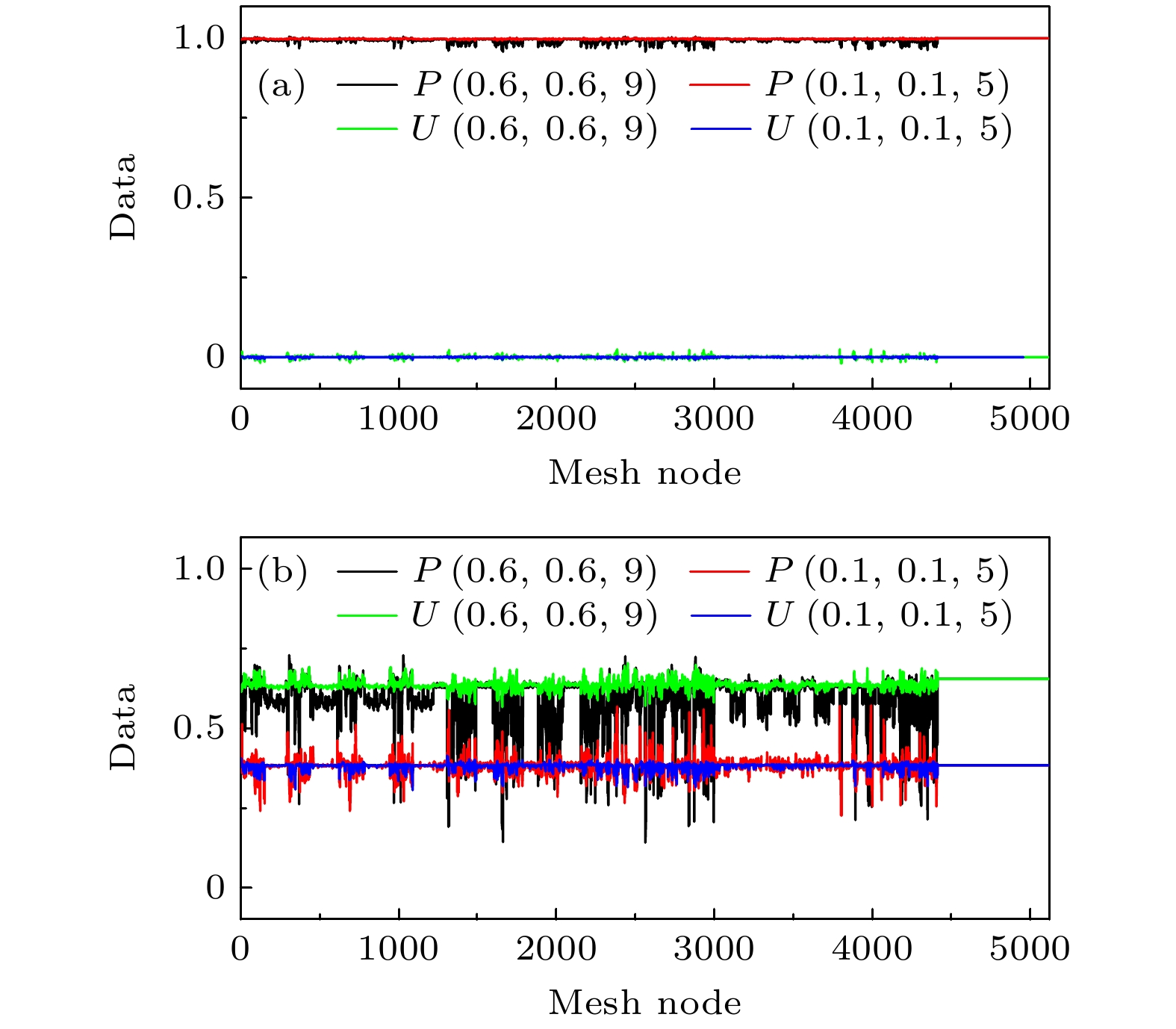
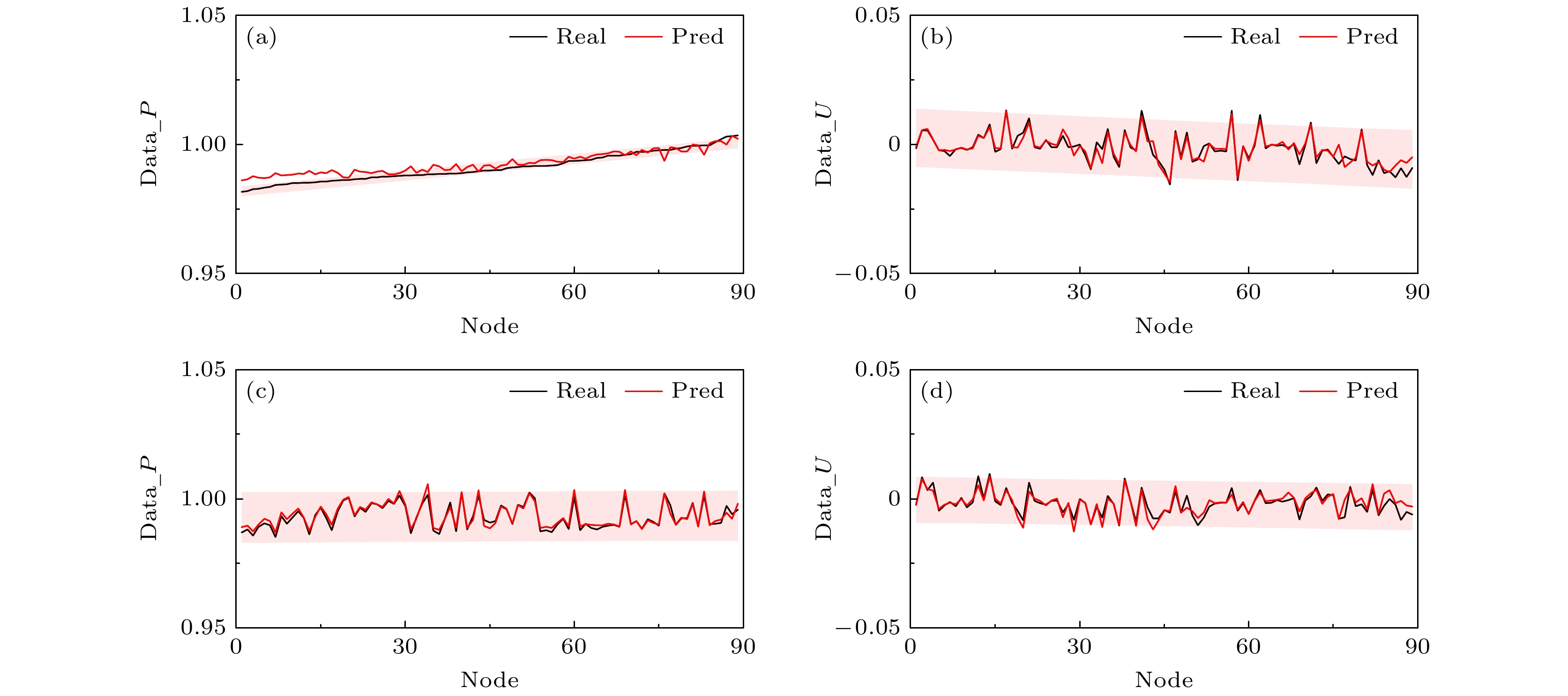
图 12 翼尖位置网格节点流场预测结果95%置信区间 (a) d1姿态压力场; (b) d1姿态速度场; (c) d3姿态压力场; (d) d3姿态速度场
Fig. 12. 95% Prediction intervals for flow field predictions at wingtip locations: (a) Dynamic pressure field for d1 configuration; (b) velocity field for d1 configuration; (c) dynamic pressure field for d3 configuration; (d) velocity field for d3 configuration.
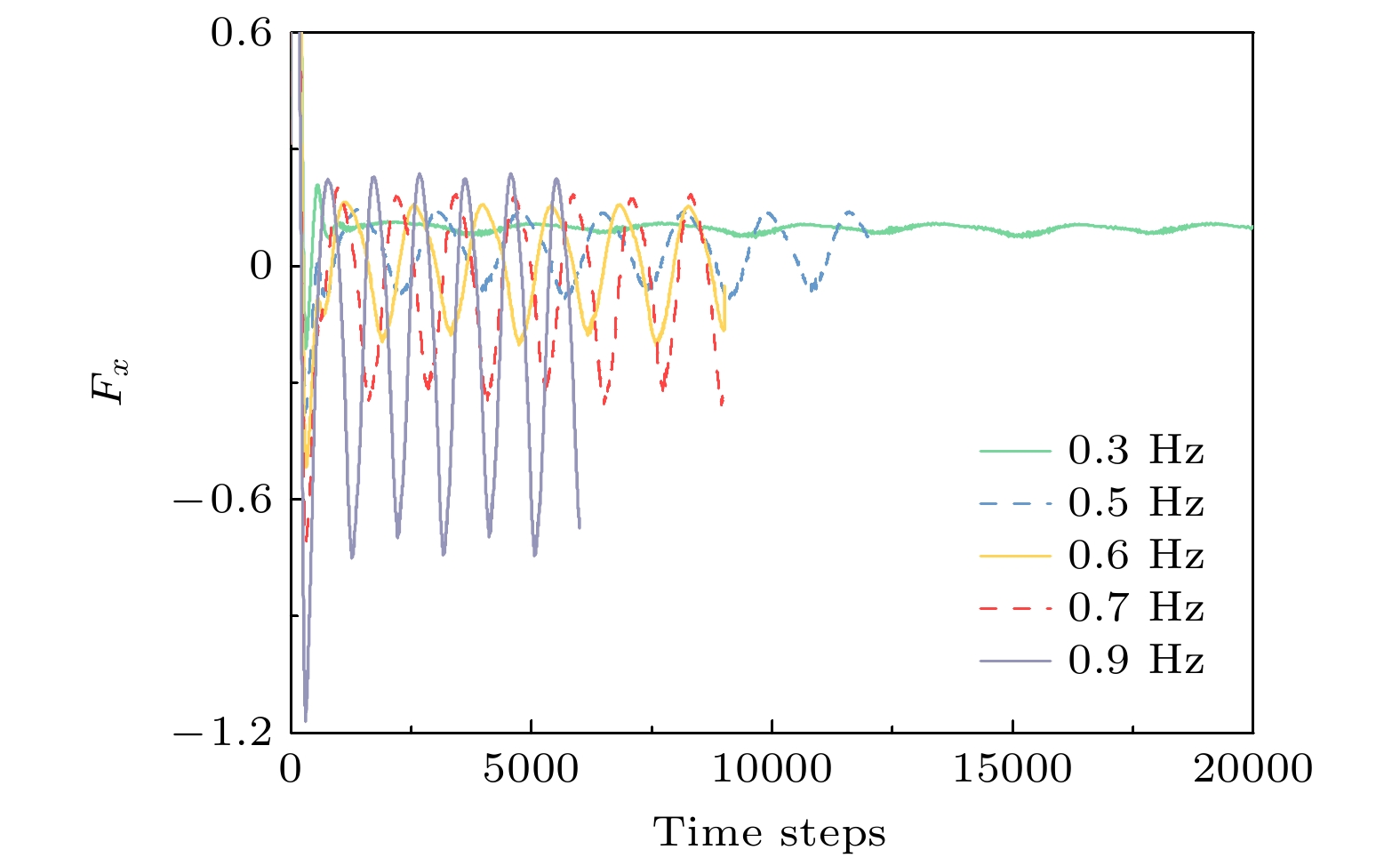
表 1 不同扑动频率对应数据提取起始与间隔时间步
Table 1. Starting times and interval steps for data extraction at different flapping frequencies.
扑动频率/Hz 起始时间步 间隔时间步 0.3 11390 57 0.5 6838 35 0.6 5698 29 0.7 4884 25 0.9 3799 19 表 2 流场预测结果准确性定量分析
Table 2. Quantitative analysis of accuracy in flow field predictions.
预测结果 内插测试工况 外推测试工况 RMSE PSNR/dB SSIM RMSE PSNR/dB SSIM d1-P 0.0224 37.031 0.9679 0.0263 36.085 0.9598 d2-P 0.0122 38.203 0.9754 0.0233 36.556 0.9624 d3-P 0.0214 37.486 0.9688 0.0208 36.387 0.9533 d1-U 0.0245 36.475 0.9613 0.0272 35.902 0.9587 d2-U 0.0146 38.811 0.9813 0.0261 35.241 0.9496 d3-U 0.0250 35.931 0.9524 0.0301 35.158 0.9571 表 3 CFD与人工智能方法预测流场效率对比
Table 3. Comparison of flow field prediction efficiency between CFD and surf-DDPM methods.
扑动频率/Hz CFD/核时 AI训练/卡时 AI预测/s 0.3 120 24 30 0.5 72 0.6 60 0.7 48 0.9 36 -
[1] 王亮 2007 博士学位论文 (南京: 河海大学)
Wang L 2007 Ph. D. Dissertation (Nanjing: Hehai University
[2] Asada T, Furuhashi H 2024 Ocean Eng. 308 118261
 Google Scholar
Google Scholar
[3] Xing C, Yin Z, Xu H, Cao Y, Qu Y, Huang Q 2024 Ocean Eng. 312 119039
 Google Scholar
Google Scholar
[4] Bao T, Cao Y, Cao Y H, Lu Y, Pan G, Huang Q G 2024 Ocean Eng. 309 118377
 Google Scholar
Google Scholar
[5] Dong H, Bozkurttas M, Mittal R, Madden P, Laude G V 2010 J. Fluid Mech. 645 34
 Google Scholar
Google Scholar
[6] Huang Z, Menzer A, Guo J, Dong H 2024 Bioinspir Biomim 19 026004
 Google Scholar
Google Scholar
[7] Wang S, Gao P, Huang Q G, Pan G, Tian X 2024 Ocean Eng. 294 116799
 Google Scholar
Google Scholar
[8] Gao P C, Song B, Huang Q G, Tian X S, Pan G, Chu Y, Bai J Y 2024 Ocean Eng. 313 119415
 Google Scholar
Google Scholar
[9] Gao P C, Huang Q G, Pan G, Cao Y, Luo Y 2023 Ocean Eng. 278 114389
 Google Scholar
Google Scholar
[10] Miyanawala T P, Li Y, Law Y Z 2024 Ocean Eng. 306 118003
 Google Scholar
Google Scholar
[11] Li G, Zhu H, Jian H 2023 J. Hydrol. 625 130025
 Google Scholar
Google Scholar
[12] 战庆亮, 葛耀君, 白春锦 2022 71 074701
 Google Scholar
Google Scholar
Zhan Q L, Ge Y J, Bai C J 2022 Acta Phys. Sin. 71 074701
 Google Scholar
Google Scholar
[13] Wang Z, Zhang W 2023 Phys. Fluids 35 025124
 Google Scholar
Google Scholar
[14] Qiu C C, Huang Q G, Pan G 2023 Phys. Fluids 35 017132
 Google Scholar
Google Scholar
[15] Xia Y, Li T, Wang Q, Yue J, Peng B, Yi X 2024 Phys. Fluids 36 103313
 Google Scholar
Google Scholar
[16] Li R, Song B, Chen Y 2024 Ocean Eng. 304 117857
 Google Scholar
Google Scholar
[17] Caraccio P, Marseglia G, Lauria A 2024 Phys. Fluids 36 107120
 Google Scholar
Google Scholar
[18] Qiu C C, Huang Q G, Pan G 2023 Ocean Eng. 281 114555
 Google Scholar
Google Scholar
[19] Gao H, Gao L, Shi Z, Sun D, Sun X 2024 Aerosp. Sci. Technol. 147 108977
 Google Scholar
Google Scholar
[20] Lin H, Jiang X, Deng X 2024 Thinking Skills and Creativity 54 101649
 Google Scholar
Google Scholar
[21] Kartashov N, Vlassis N N 2024 arXiv: 2409.14473 [cs.CE]
[22] Torem N, Ronen R, Schechner Y Y, Elad M 2023 Proceedings of the IEEE/CVF International Conference on Computer Vision Paris, France, October 2–6, 2023 p3810
[23] Ho J, Jain A, Abbeel P 2020 Adv. Neural Inf. Process. Syst. 33 6840
 Google Scholar
Google Scholar
[24] Rombach R, Blattmann A, Loren D, Esser P, Ommer B 2022 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition New Orleans, LA, June 18–24, 2022 p10674
[25] Song J, Meng C, Ermon S 2020 arXiv: 2010.02502 [cs.LG]
[26] Nichol A, Dhariwal P, Ramesh A, Shyam P, Mishkin P, McGrew B 2021 arXiv: 2112.10741 [cs.CV]
[27] Huang L, Zheng C, Chen Y 2024 Phys. Fluids 36 095113
 Google Scholar
Google Scholar
[28] Rybchuk A, Hassanaly M, Hamilton N 2023 Phys. Fluids 35 126604
 Google Scholar
Google Scholar
[29] Gao P C, Tian X, Huang Q G 2024 Phys. Fluids 36 011902
 Google Scholar
Google Scholar
[30] Gao P C, Huang Q G, Pan G 2023 Phys. Fluids 35 061909
 Google Scholar
Google Scholar
[31] 张栋 2020 博士学位论文 (西安: 西北工业大学)
Zhang D 2020 Ph. D. Dissertation (Xi’an: Northwestern Polytechnical University
计量
- 文章访问数: 981
- PDF下载量: 41
- 被引次数: 0













 下载:
下载: