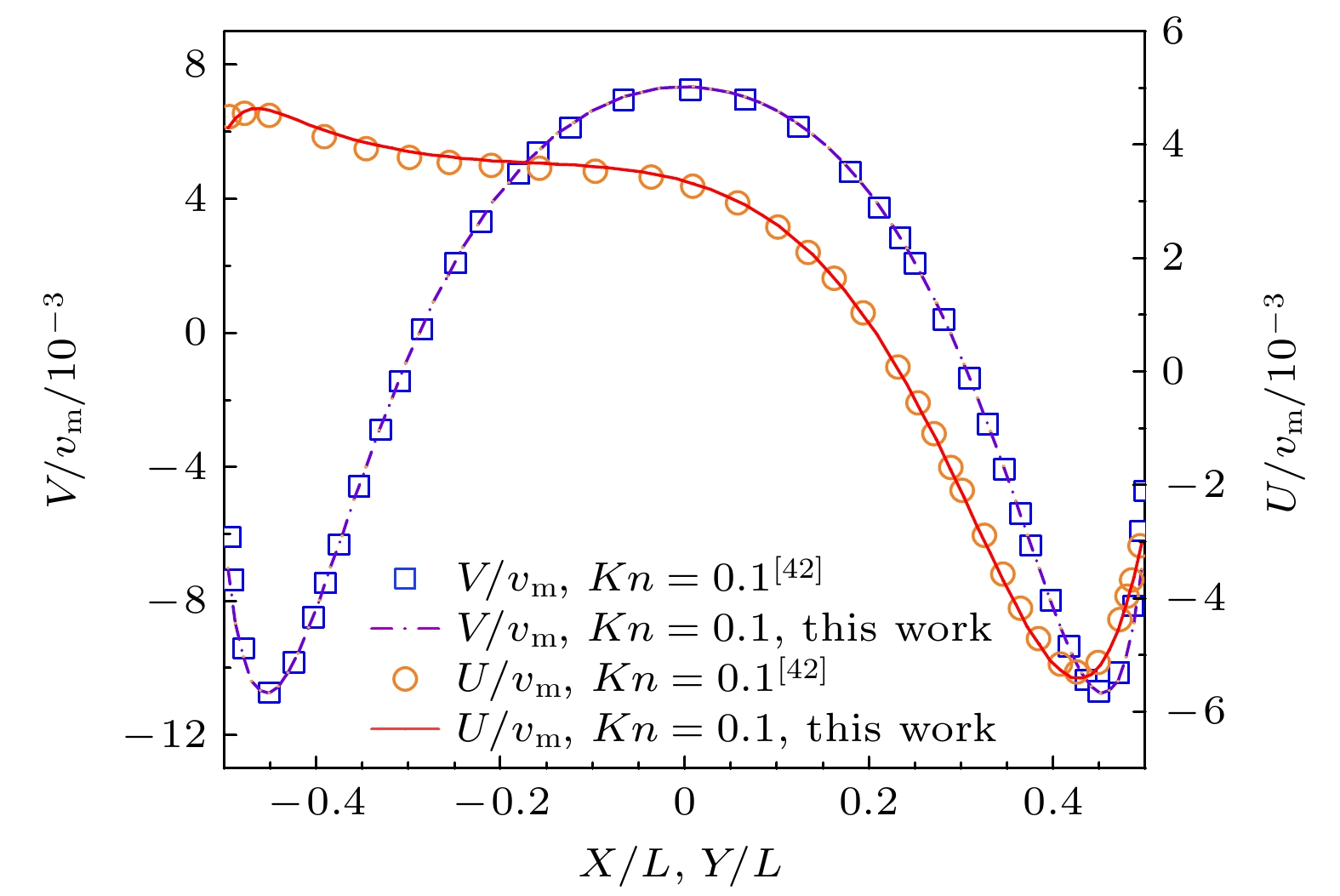
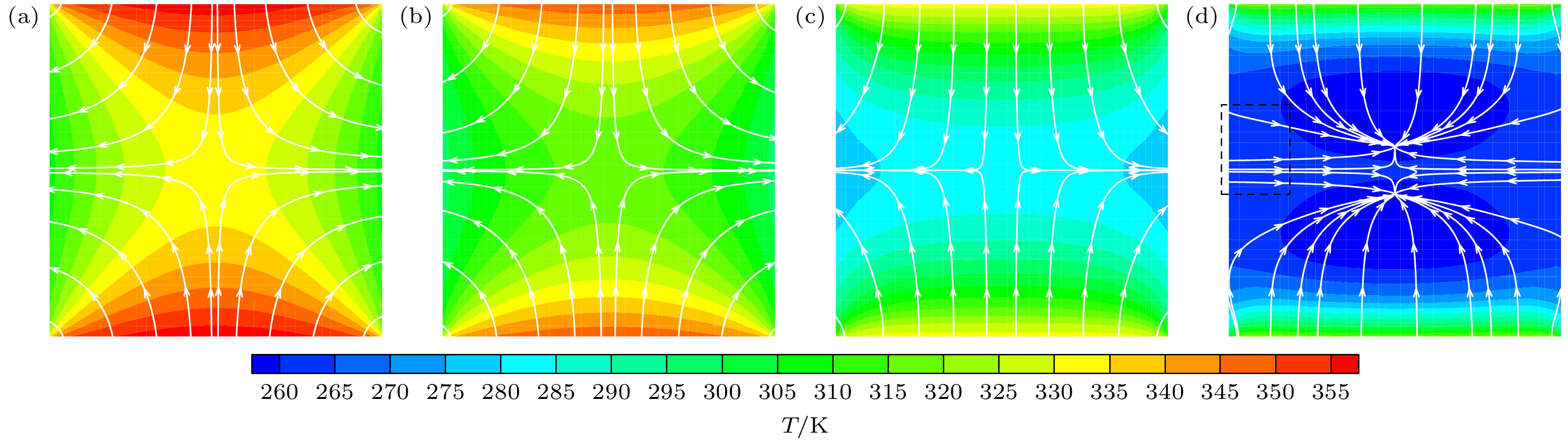
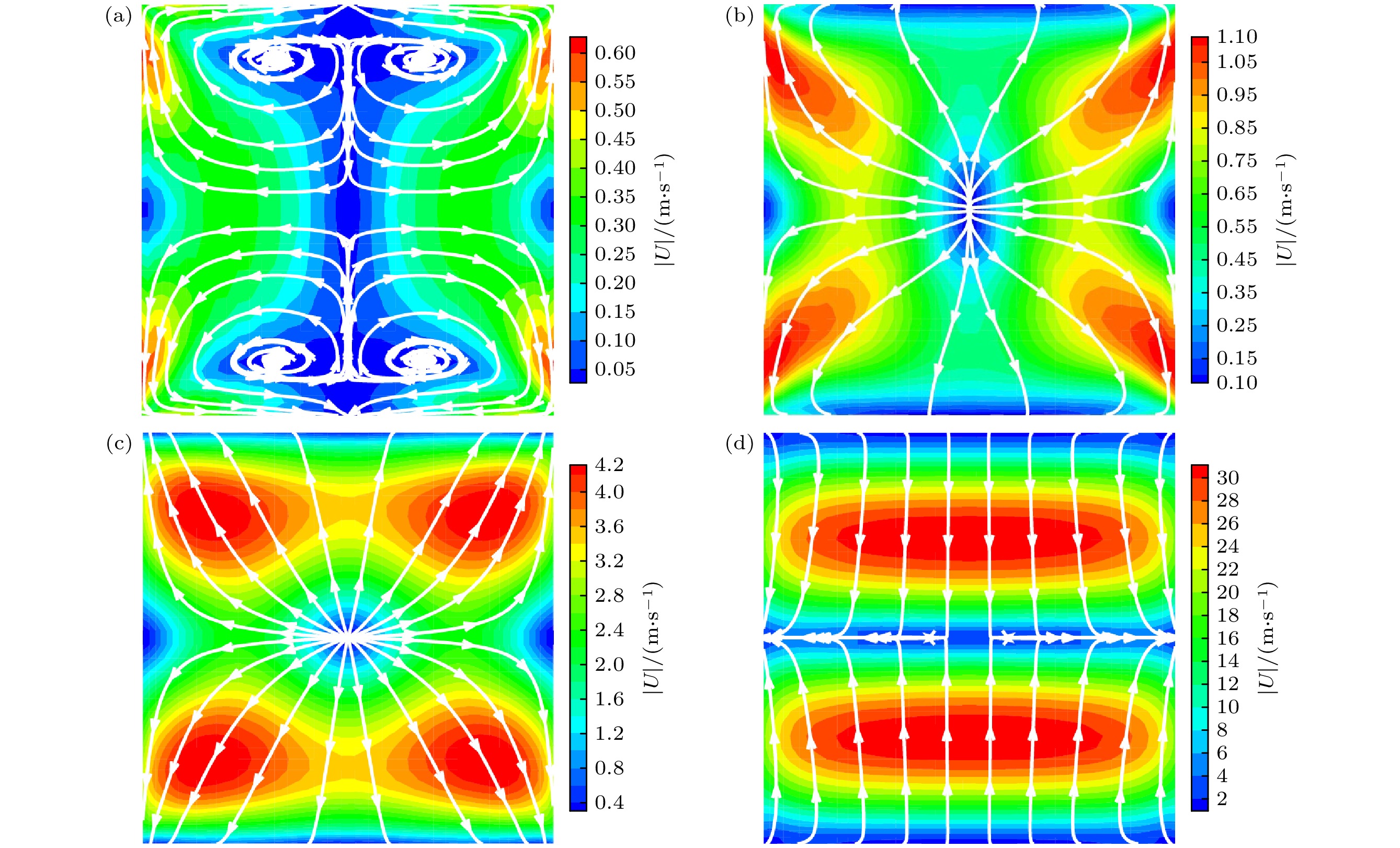
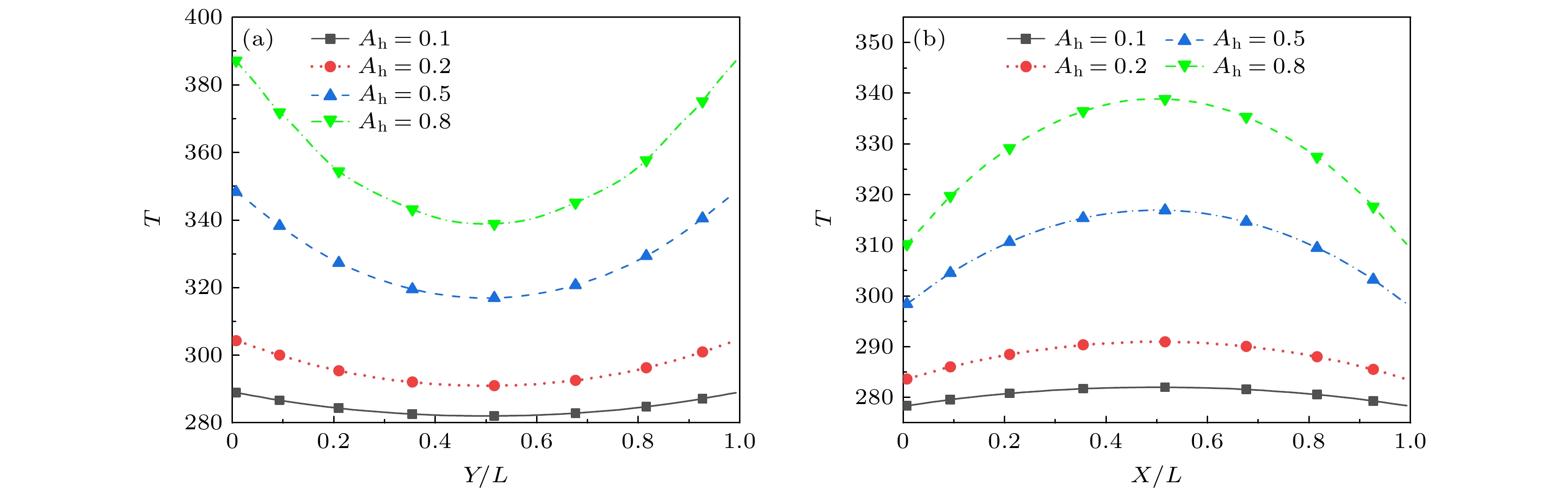
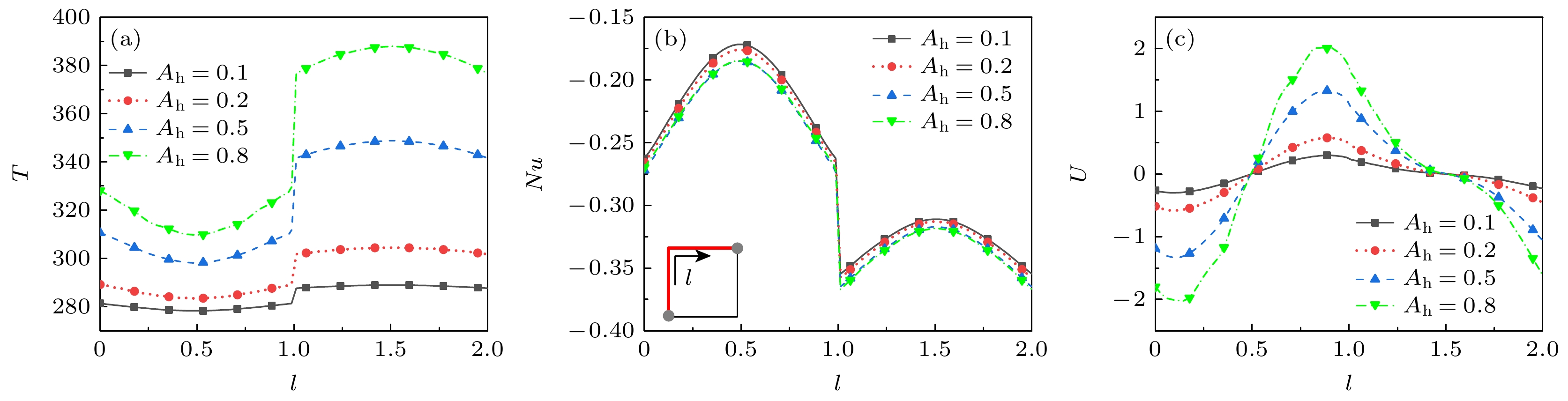
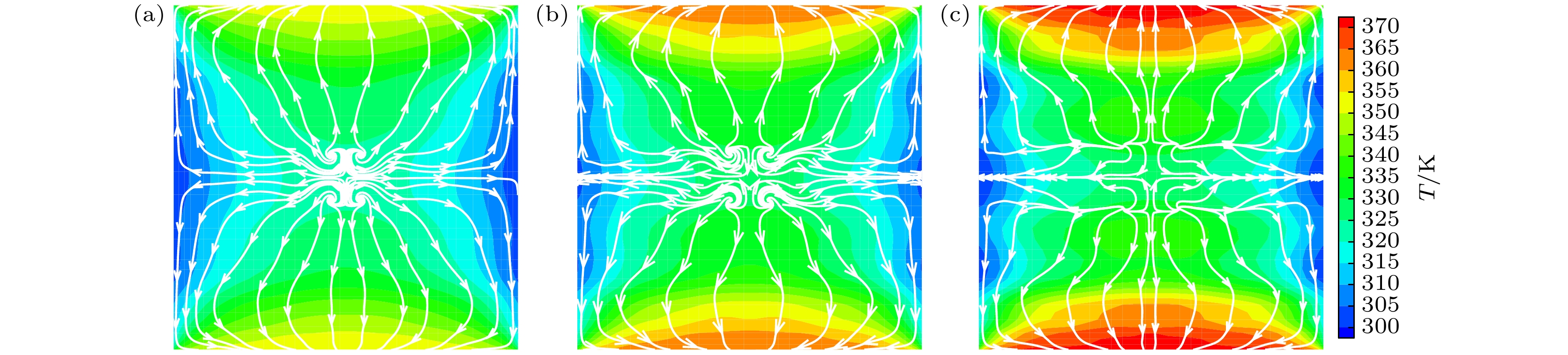
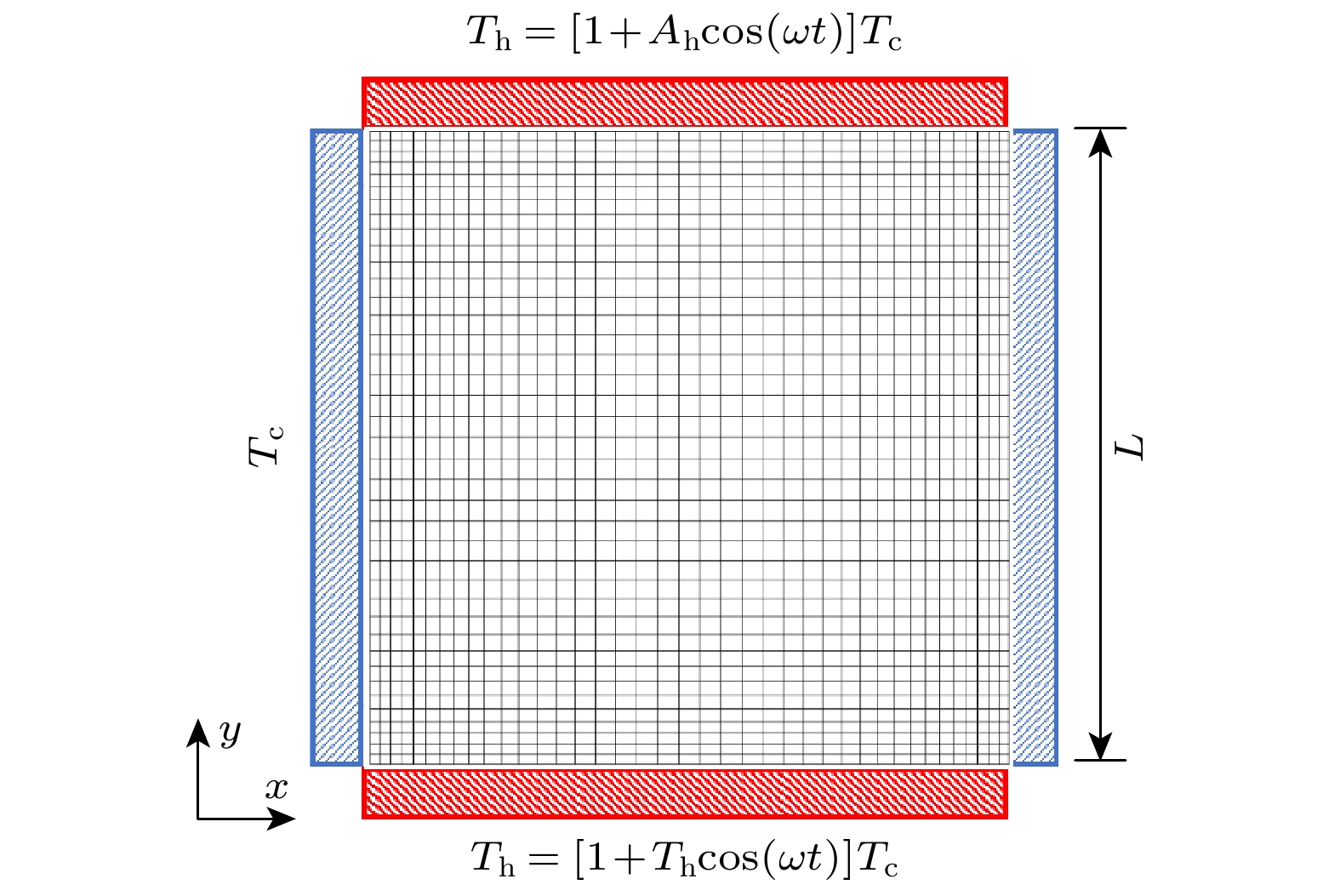
-
为考察壁面温度变化对受限空间内稀薄气体流动与传热特性的影响, 采用离散气体动理学格式(DUGKS)模拟研究了方腔内的热蠕流动. 腔体四周为静止漫反射恒温壁面, 上、下壁温度则随时间周期性变化. 模拟的参数范围如下: 变温频率0.5 ≤ St ≤ 5.0、变温振幅0.1 ≤ Ah ≤ 0.8和克努森数0.01 ≤ Kn ≤ 10. 数值结果表明: 方腔内气体流动与传热特性呈现周期性变化, 且不会出现反傅里叶热传递. 变温频率、振幅和克努森数的提高均可增强腔内热蠕流动强度, 且变温壁面附近速度滑移和温度跳跃增大. St和Kn的增大导致出现传热滞后现象, 壁面换热能力减弱. 特别地, 当St = 0.5较小时腔内观察到复杂涡流结构; St = 5.0时气体由变温壁面向腔体水平中心线均匀流动, 涡流消失的同时左、右壁面中点附近由吸热区转变为放热区. Ah增大时腔内温度场和速度场结构变化不大, 而壁面传热强度减小.In order to examine the influence of wall temperature change on the flow and heat transfer properties of rarefied gas in restricted space, the discrete unified gas kinetic scheme (DUGKS) is used to simulate the thermal creep flows in a square cavity. All the boundaries of the cavity are stationary diffuse reflection walls. The temperature of left wall and right wall are lower, and the temperature of the upper wall and the lower wall are both subjected to periodic variation. The simulation parameters considered in the present work are set as follows: the Knudsen number Kn is in a range 0.01–10, temperature change frequency St in a range of 0.5–5, and temperature change amplitude Ah in a range of 0.1–0.8. The results indicate that the velocity field and temperature field in the cavity exhibit periodic variations. No inverse Fourier heat transfer phenomenon is observed within the parameter ranges studied. The intensity of the thermal creep flow can be increased by increasing the frequency, temperature, and the Knudsen number. This can also raise the temperature jump and velocity slip close to the temperature change walls. Heat transfer lag and a reduction in the heat transfer capability of the wall are caused by increasing St and Kn. When St is small, say, St = 0.5, a complex vortex structure is seen in the cavity. As the value of St rises to 5, the vortex disappears, the gas travels from the variable temperature wall to the horizontal centerline of cavity, and the region close to the middle of the left wall and right wall changes from an endothermic zone to an exothermic zone. Furthermore, the temperature field and velocity field inside the cavity hardly change, but the degree of heat transfer on the wall decreases with the increase of Ah. The main results are shown in the figure attached below. This work provides helpful recommendations for designing the MEMS devices by using pulsed heating.
-
Keywords:
- thermal creep flows /
- discrete unified gas kinetic scheme /
- thermally induced oscillating flow /
- diffuse boundary
-
图 1 变温壁面驱动方腔流动示意图
Fig. 1. Schematic diagram of the flow of a variable temperature wall driven cavity.
图 3 通过左侧一级主涡中心的水平和竖直线上的U和V速度分布
Fig. 3. U and V velocity distribution in horizontal and vertical lines through the center of the primary vortex on the left.
图 4 Kn = 1, Ah = 0.5, t = 0时, 不同St下方腔内温度场和热流线 (a) St = 0.5; (b) St = 1.0; (c) St = 2.0; (d) St = 5.0
Fig. 4. Temperature field and thermal flow lines in different cavities under different St when Kn = 1, Ah = 0.5 and t = 0: (a) St = 0.5; (b) St = 1.0; (c) St = 2.0; (d) St = 5.0.
图 5 Kn = 1, Ah = 0.5, t = 0时不同频率St下中心线上的温度分布 (a)竖直中心线X/L = 0.5; (b): 水平中心线Y/L = 0.5
Fig. 5. Temperature distribution on the centerline at different frequencies St when Kn = 1, Ah = 0.5 and t = 0: (a) Vertical centerline X/L = 0.5; (b) horizontal centerline Y/L = 0.5.
图 6 Kn = 1, Ah = 0.5, t = 0时不同频率St下方腔内速度云图和流线 (a) St = 0.5; (b) St = 1.0; (c) St = 2.0; (d) St = 5.0
Fig. 6. Intracavity velocity contours and streamlines below St at different frequencies when Kn = 1, Ah = 0.5 and t = 0: (a) St = 0.5; (b) St = 1.0; (c) St = 2.0; (d) St = 5.0.
图 7 Kn = 1, Ah = 0.5, t = 0时不同St时左、上壁面处气体温度T、努塞尔数Nu和速度U分布
Fig. 7. Distributions of gas temperature T, Nusselt number Nu and velocity U on the left and upper walls at different St when Kn = 1, Ah = 0.5 and t = 0.
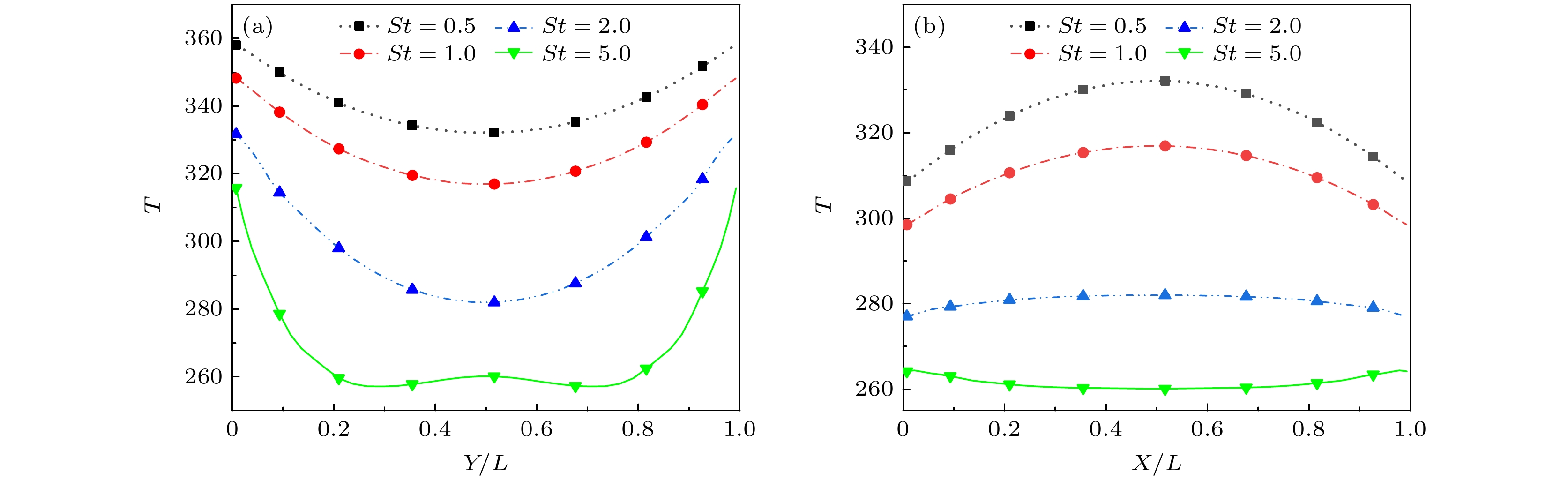
图 8 Ah = 0.5, t = 0时不同参数在不同St和Kn下的变化 (a)左壁面中点温度Tcy; (b)上壁面中点温度Tcx; (c)左壁面中点努塞尔数Nucy; (d)左壁面下半部分平均速度$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $
Fig. 8. Variations of different parameters under different St and Kn when Ah = 0.5 and t = 0: (a) Temperature of the midpoint of the left wall Tcy; (b) temperature of the midpoint of the upper wall Tcx; (c) Nussel number of the midpoint of the left wall Nucy; (d) the average velocity of the lower half of the left wall $ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $ .
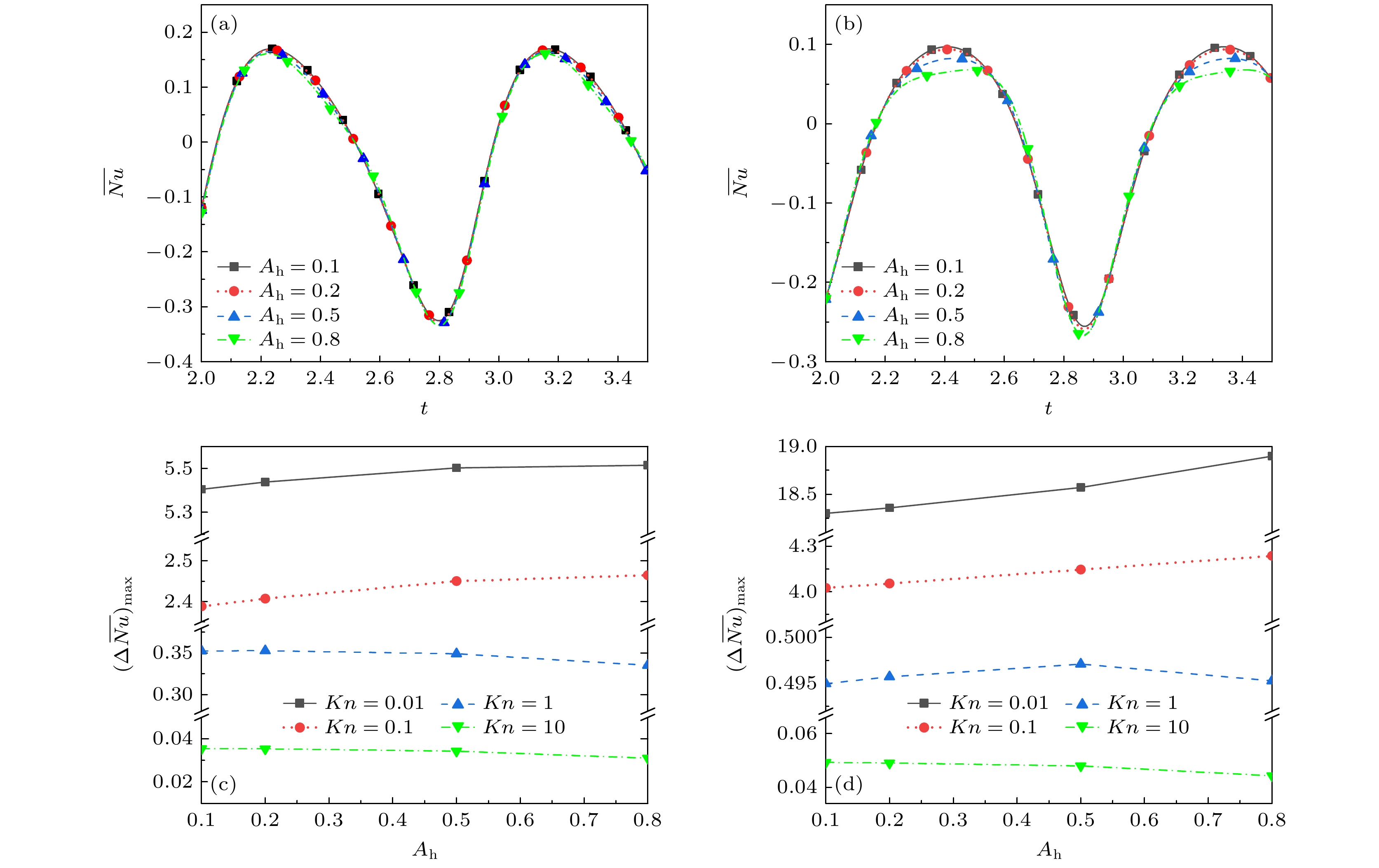
图 9 不同St和Kn下, 壁面平均努塞尔数$\overline{Nu} $的时间历程及$\overline{Nu} $的极差$ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $ (a), (c) Y = 0, 下壁面; (b), (d) X = 0, 左壁面
Fig. 9. The time history of the average Nussel number $\overline{Nu} $and the range $ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $of $\overline{Nu} $on the wall under different St and Kn: (a), (c) Lower wall surface, Y = 0; (b), (d) left wall, X = 0.
图 10 Ah = 0.2, Kn = 1, St = 1.0, t = 0时方腔内的温度场和热流线(a)、速度场和流线(b)
Fig. 10. Temperature field and thermal streamlines (a), velocity field and streamlines (b) in a square cavity at Kn = 1, St = 1.0, Ah = 0.2 and t = 0.
图 11 Kn = 1, St = 1.0, t = 0时不同振幅Ah的中心线上温度分布 (a)竖直中心线X/L = 0.5; (b)水平中心线Y/L = 0.5
Fig. 11. Temperature distribution on the centerline of Ah with different amplitudes when Kn = 1, St = 1.0 and t = 0: (a) Vertical centerline X/L = 0.5; (b) horizontal centerline Y/L = 0.5.
图 12 Kn = 1, St = 1.0, t = 0时不同Ah时左、上壁面处气体温度T, 努塞尔数Nu和速度U分布
Fig. 12. Distribution of gas temperature T, Nusselt number Nu and velocity U on the left and upper wall surfaces at different Ah when Kn = 1, St = 1.0 and t = 0.
图 13 St = 1.0, t = 0时, 不同参数在不同Ah和Kn下的变化 (a)左壁面中点温度Tcy; (b)上壁面中点温度Tcx; (c)左壁面中点努塞尔数Nucy; (d)左下半壁面平均速度$ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $
Fig. 13. Variations of different parameters under different Ah and Kn when St = 1.0 and t = 0: (a) The midpoint temperature of the left wall Tcy; (b) temperature of the midpoint of the upper wall Tcx; (c) Nusselt number of the left wall midpoint Nucy; (d) the average velocity of the lower left half of the wall $ {\overline{U}}_{{\mathrm{z}}{\mathrm{x}}} $.
图 14 Kn = 10, St = 1.0, t = 0时, 不同Ah下方腔内温度云图和流线 (a) Ah = 0.6; (b) Ah = 0.7; (c) Ah = 0.8
Fig. 14. Temperature cloud maps and streamlines in the cavity with different Ah values at Kn = 10, St = 1.0, and t = 0: (a) Ah = 0.6; (b) Ah = 0.7; (c) Ah = 0.8.
图 15 St = 1.0时不同Ah和Kn下, 壁面平均努塞尔数$\overline{Nu} $的时间历程及$\overline{Nu} $的极差$ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $. (a), (c) X = 0, 左壁面; (b), (d) Y= 0, 下壁面
Fig. 15. The time history of the average Nussel number $\overline{Nu} $ and the range $ {\left(\Delta\overline{Nu}\right)}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $of $\overline{Nu} $ on the wall under different Ah and Kn when St = 1.0: (a), (c) Left wall, X = 0; (b), (d) lower wall surface, Y= 0.
-
[1] 沈青 2006 力学进展 36 142
Google Scholar
Shen Q 2006 Adv. Mech. 36 142
Google Scholar
[2] Frangi A, Frezzotti A, Lorenzani S 2007 Comput. Struct. 85 810
Google Scholar
[3] 梅涛, 陈占秀, 杨历, 朱洪漫, 苗瑞灿 2020 69 224701
Mei T, Chen Z X, Yang L, Zhu H M, Miao R C Acta Phys. Sin. 69 224701
[4] Ramadan K M, Qisieh O, Tlili I 2022 Proc. Inst. Mech. Eng. Part C 236 5033
Google Scholar
[5] Mousivand M, Roohi E 2022 Phys. Fluids 34 052002
Google Scholar
[6] Lan J, Xie J, Ye J, Peng W Z, Jiao X Y 2022 Int. J. Hydrogen Energy 47 19206
Google Scholar
[7] 韩峰, 王晓伟, 张文青, 张世伟, 张志军 2023 真空科学与技术学报 43 238
Hang F, Wang X W, Zhang W Q, Zhang S W, Zhang Z J 2023 J. Vac. Sci. Technol. 43 238
[8] 王晓伟, 张志军, 张文青, 苏天一, 张世伟 2020真空与低温 26 73
Wang X W, Zhang Z J, Zhang W Q, Su T Y, Zhang S W 2020 Vac. Cryogen
[9] Wu L, Zhang Y H, Li Z H 2017 Sci. Sin. phys. Mech. As. 47 070004
Google Scholar
[10] Tsimpoukis A, Vasileiadis N, Tatsios G, Valougeorgis D 2019 Phys. Fluids 31 067108
Google Scholar
[11] Taassob A, Kamali R, Bordbar A 2018 Vacuum 151 197
Google Scholar
[12] Nabapure D 2021 J. Comput. Sci. Neth. 49 101276.
Google Scholar
[13] Wu L, Reese J M, Zhang Y 2014 J. Fluid Mech. 748 350
Google Scholar
[14] Ogata Y, Kawaguchi T 2011 J. Fluid Sci. Technol. 6 215
Google Scholar
[15] Palharini R C, Scanlon T J, White C 2018 Comput. Fluids 165 173
Google Scholar
[16] Yang W Q, Tang S, Yang H 2019 Appl. Sci. 9 2733
Google Scholar
[17] 单小东, 王沫然 2013 工程热 34 2159
Shan X D, Wang M R 2013 J. Eng. Thermophys. 34 2159
[18] 张帅, 方蜀州, 许阳 2021 推进技术 42 2002
Zhang S, Fang S Z, Xu Y 2021 J. Propul. Technol. 42 2002
[19] Zhang J, Yao S Q, Fei F, Ghalambaz M, Wen D S 2020 Phys. Fluids 32 102001
Google Scholar
[20] Moghadam E Y, Roohi E, Esfahani J A 2014 Vacuum 109 333
Google Scholar
[21] Yamaguchi H, Perrier P, Ho M T, Méolans J G, Niimi T, Graur I 2016 J. Fluid Mech. 795 690
Google Scholar
[22] Barbera E, Brini F 2018 Europhys. Lett. 120 34001
[23] Akhlaghi H, Roohi E, Stefanov S 2018 Sci. Rep. 8 13533
Google Scholar
[24] Han Y L 2010 Fluid Dyn. Res. 42 045505
Google Scholar
[25] Zhu M B, Roohi E, Ebrahimi A 2023 Phys. Fluids 35 052012
Google Scholar
[26] Roohi E, Shahabi V, Bagherzadeh A 2018 Int. J. Therm. Sci. 125 381
Google Scholar
[27] Wang P, Zhu L H, Su W, Wu L, Zhang Y H 2018 Phys. Rev. E 97 043103
Google Scholar
[28] Zhu L H, Guo Z L, Xu K 2016 Comput. Fluids 127 211
Google Scholar
[29] Wang X W, Su T Y, Zhang W Q, Zhang Z J, Zhang S W 2020 Microsyst. Nanoeng. 6 26
Google Scholar
[30] 张贝豪, 郑林 2020 69 164401
Google Scholar
Zhang B H, Zheng L 2020 Acta Phys. Sin. 69 164401
Google Scholar
[31] Ou Y, Qu F, Wang G Y, Nie M Y, Li Z G, Ou W, Xie C Q 2016 Appl. Phys. Lett. 109 023512
Google Scholar
[32] 万启坤, 张月, 郭照立 2023 计算物理 40 653
Wan Q K, Zhang Y, Guo Z L 2023 J. Chin. J. Comput. Phys. 40 653
[33] Kalempa D, Sharipov F, Silva J C 2019 Vacuum 159 82
Google Scholar
[34] Bargatin I, Kozinsky I, Roukes M L 2007 Appl. Phys. Lett. 90 093116
Google Scholar
[35] Ilic B, Yang Y, Aubin K, Reichenbach R, Krylov S, Craighead H G 2005 Nano Lett. 5 925
Google Scholar
[36] Juvé V, Crut A, Maioli P, Pellarin M, Broyer M, Del Fatti N, Vallée F 2010 Nano Lett. 10 1853
Google Scholar
[37] Guo Z L, Wang R J, Xu K 2015 Phys. Rev. E 91 033313
Google Scholar
[38] 孙喜明, 姚朝晖, 杨京龙 2002 51 1942
Google Scholar
Sun X M, Yao Z H, Yang J L 2002 Acta Phys. Sin. 51 1942
Google Scholar
[39] 孙佳坤, 林传栋, 苏咸利, 谭志城, 陈亚楼, 明平剑 2024 73 110504
Google Scholar
Sun J K, Lin C D, Su X L, Tan Z C, Chen Y L, Ming P J 2024 Acta Phys. Sin. 73 110504
Google Scholar
[40] Huang J C, Xu K, Yu P 2013 Commun. Comput. Phys. 14 1147
Google Scholar
[41] Wang Y, Zhong C W, Liu S 2019 Phys. Rev. E 100 063310
Google Scholar
[42] Zhu L H, Chen S Z, Guo Z L 2017 Comput. Phys. Commun. 213 155
Google Scholar
[43] Vargas M, Tatsios G, Valougeorgis D, Stefanov S 2014 Phys. Fluids 26 057101
Google Scholar
下载:
计量
- 文章访问数: 340
- PDF下载量: 12
- 被引次数: 0
