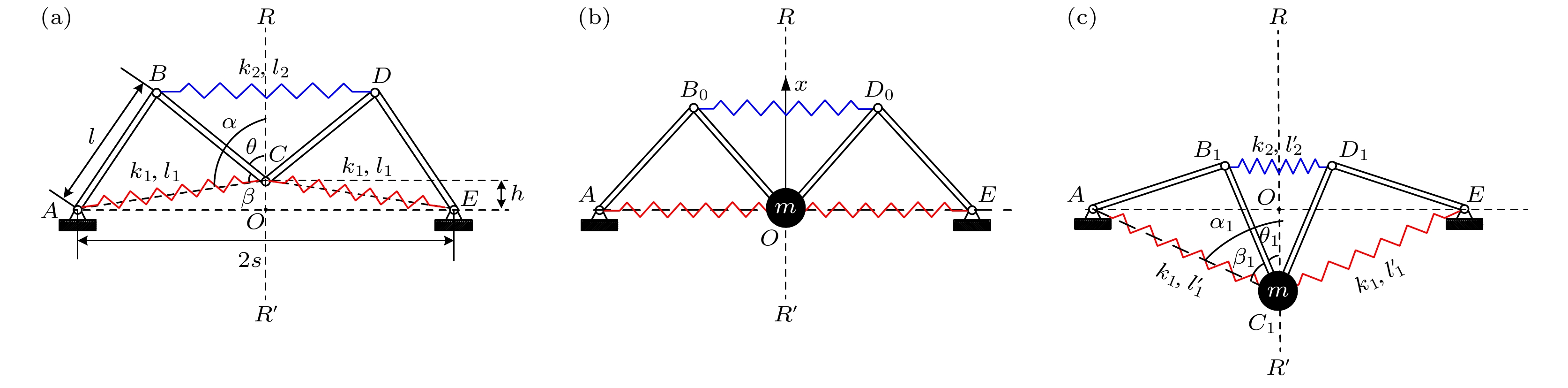
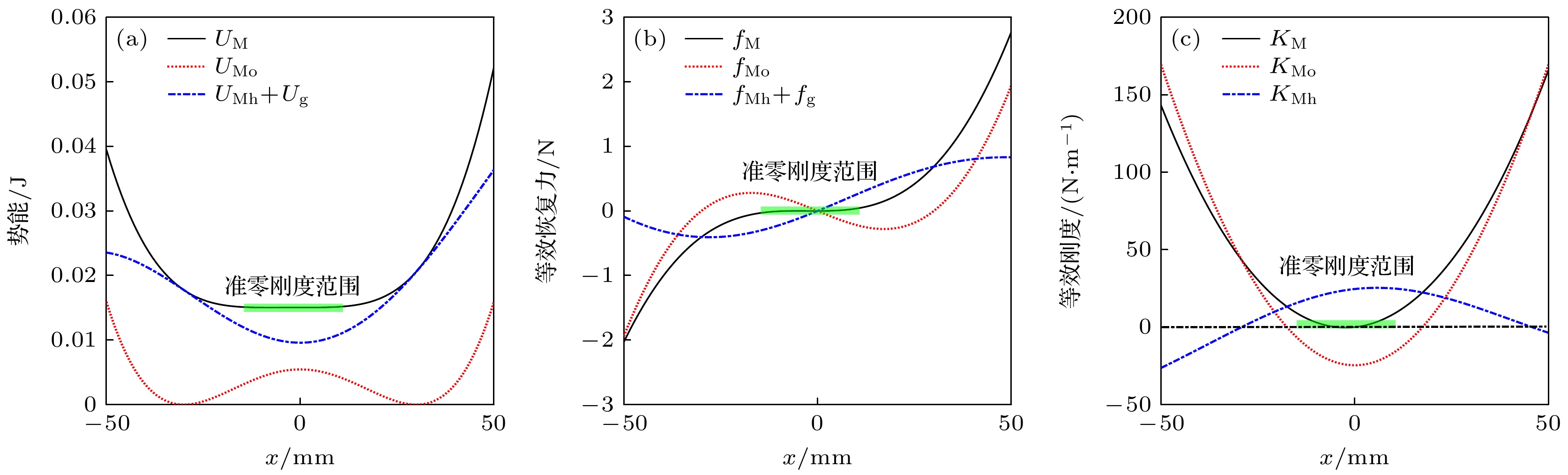
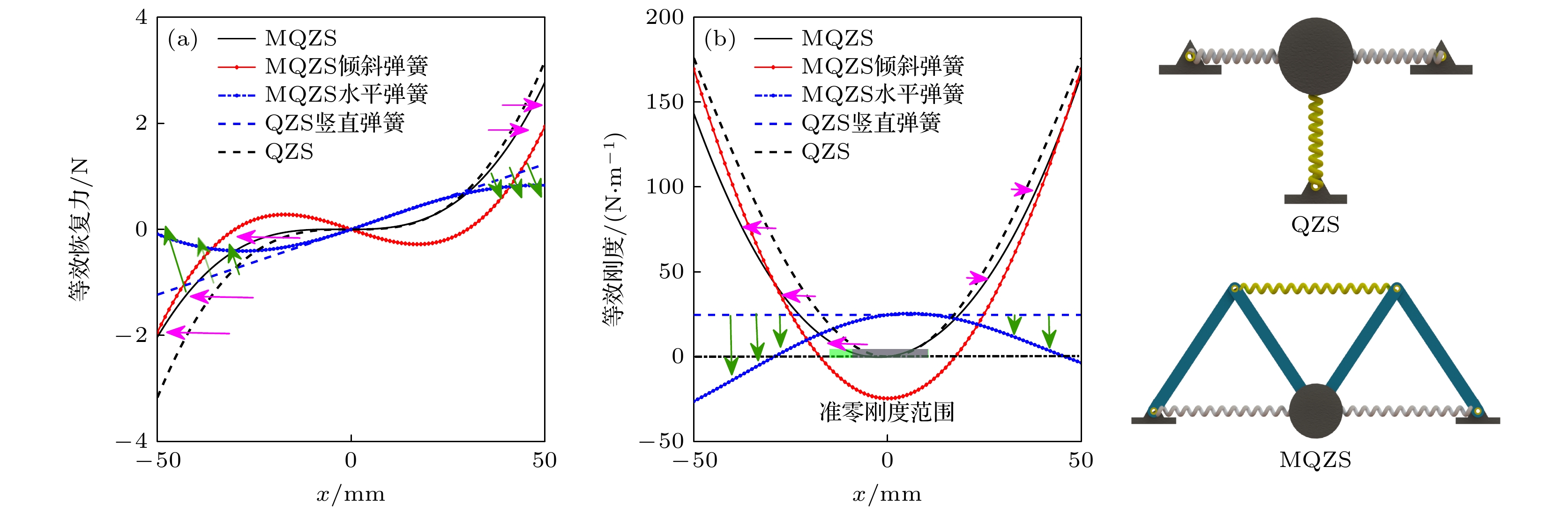
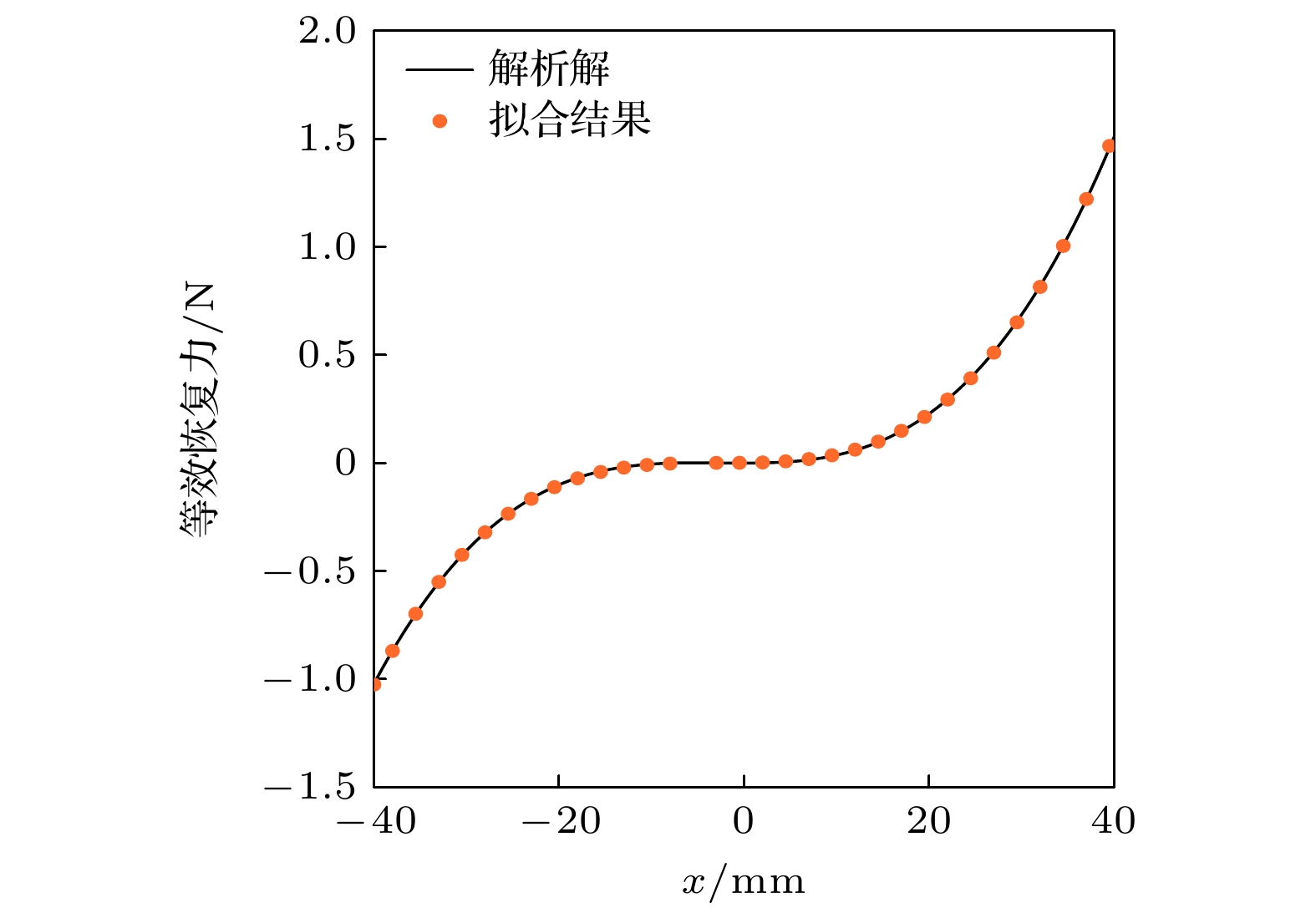
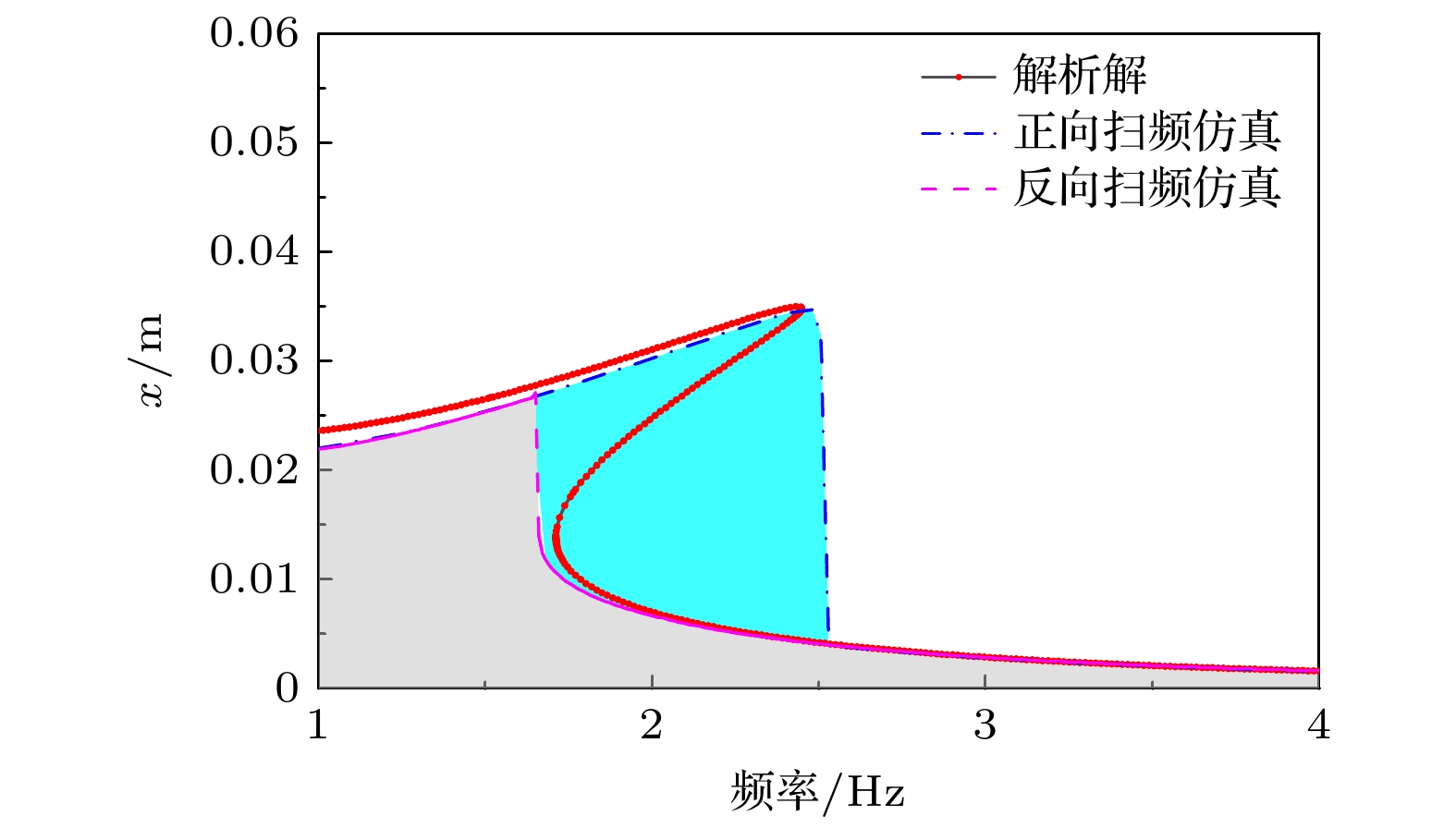
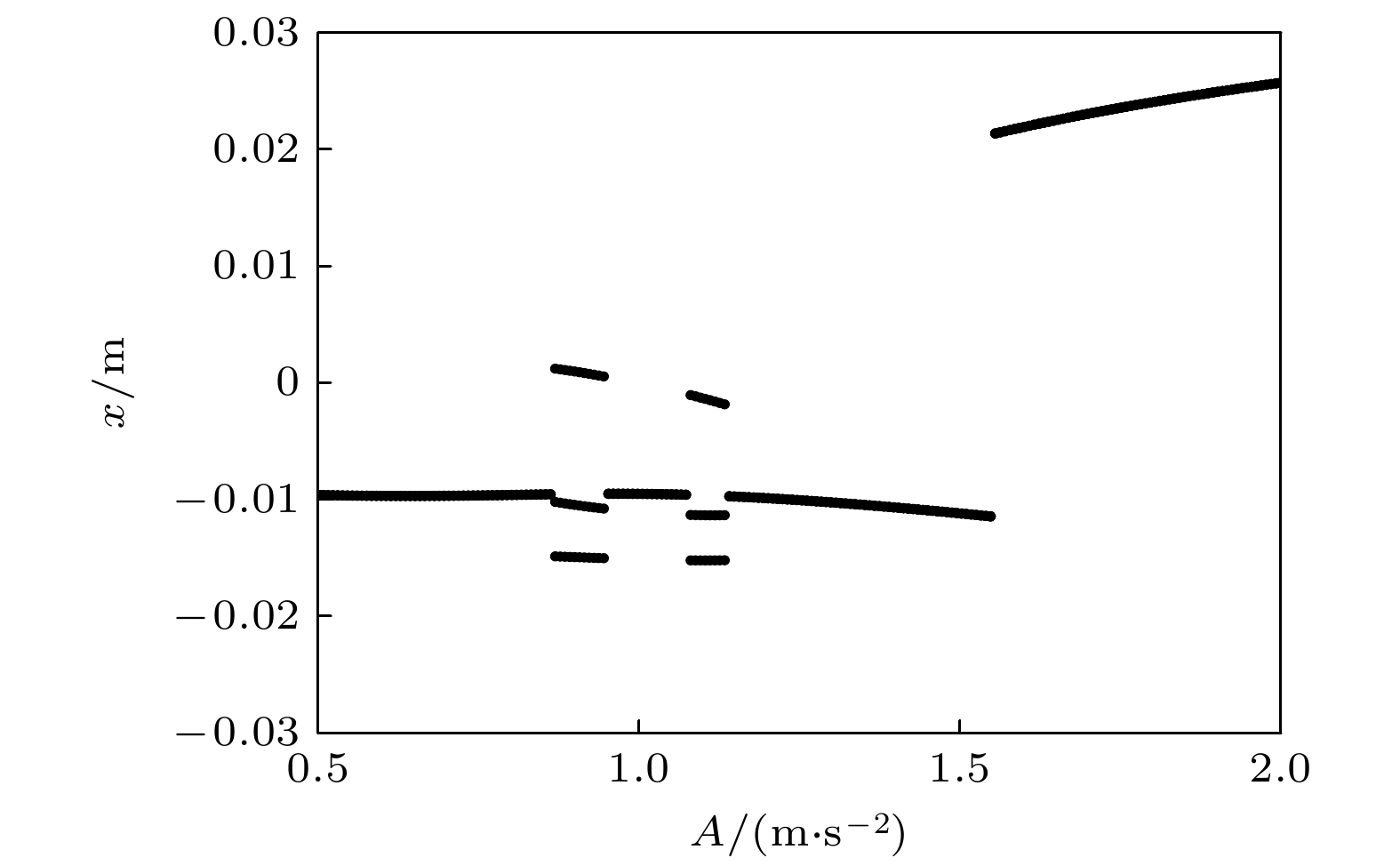
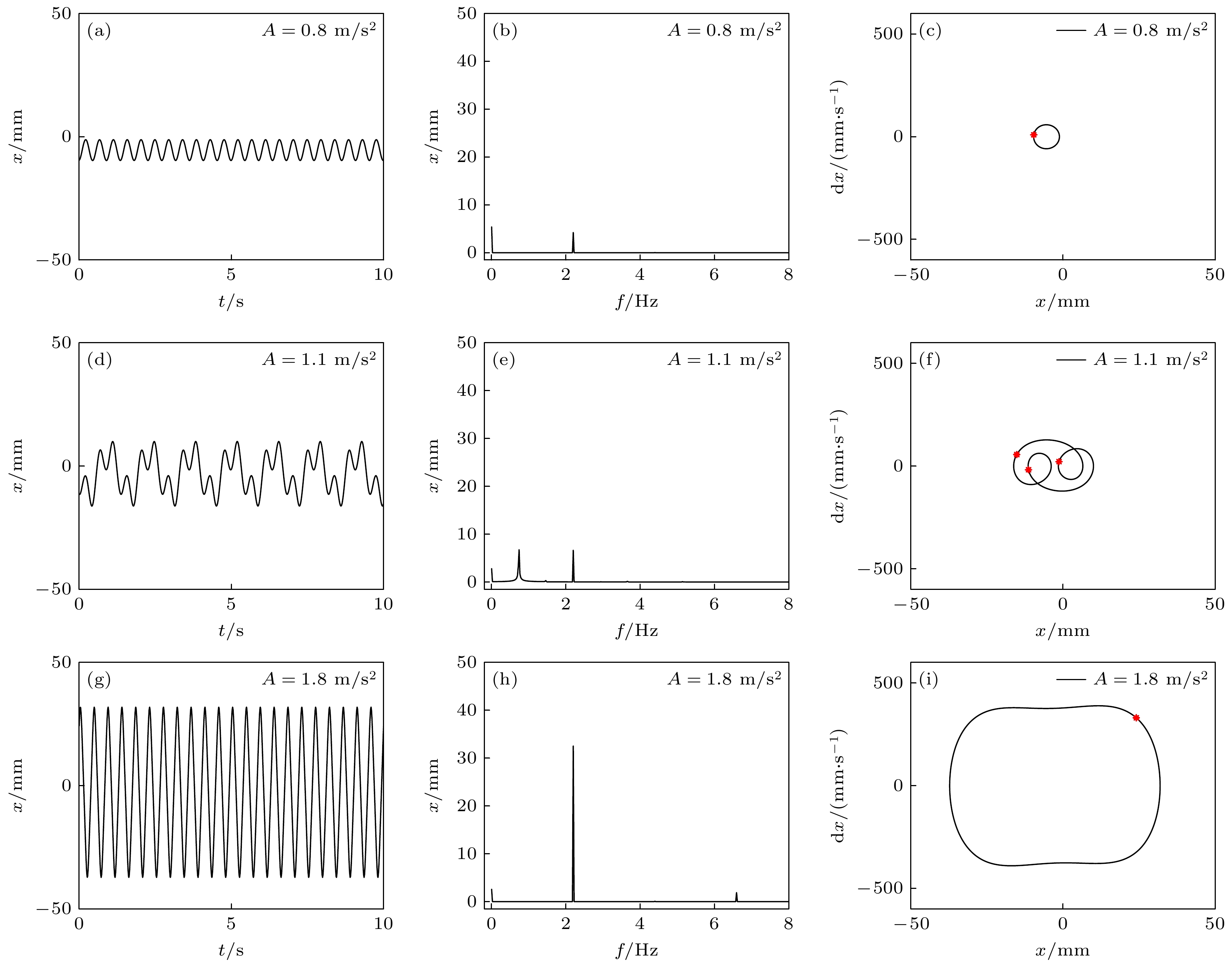
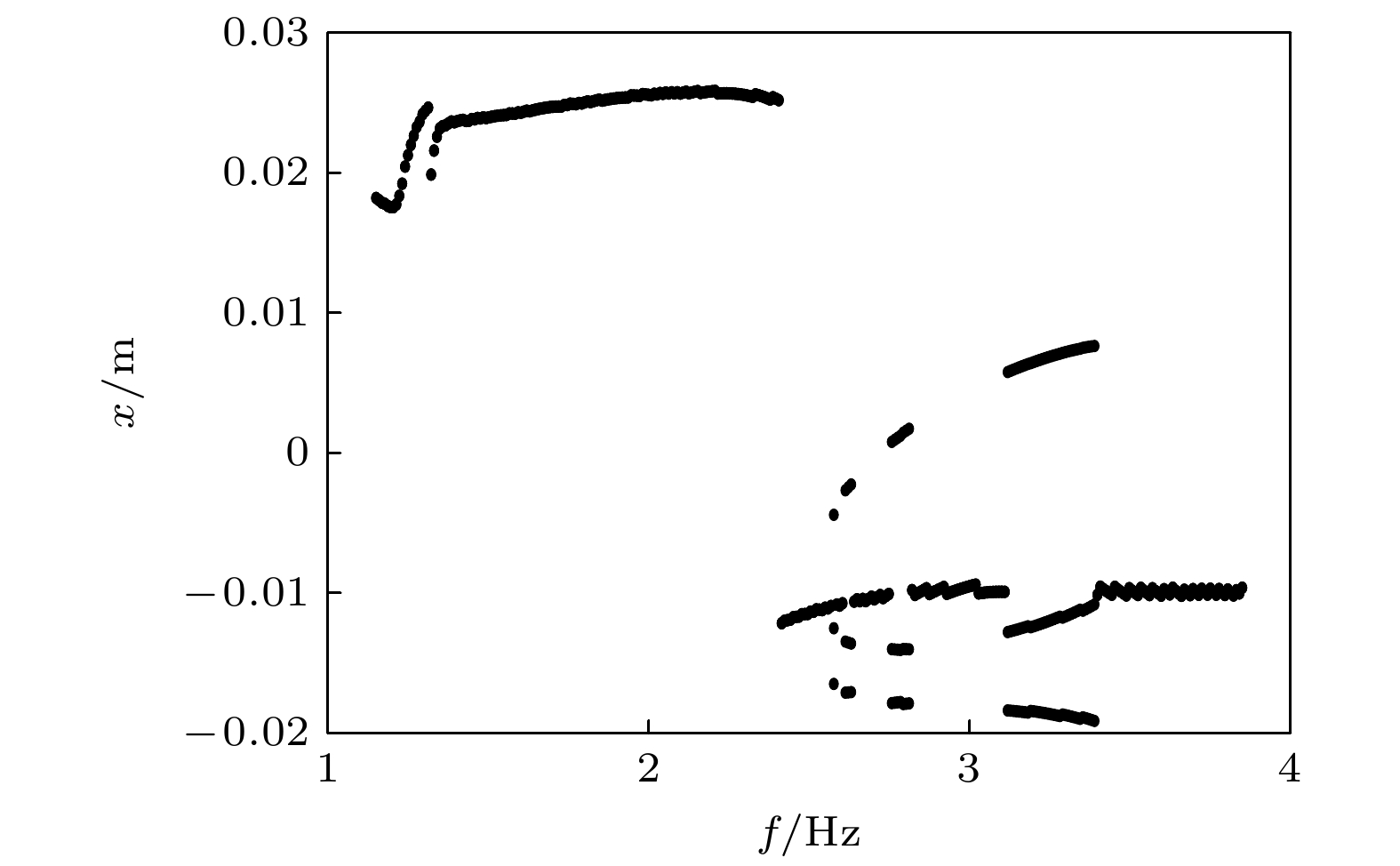
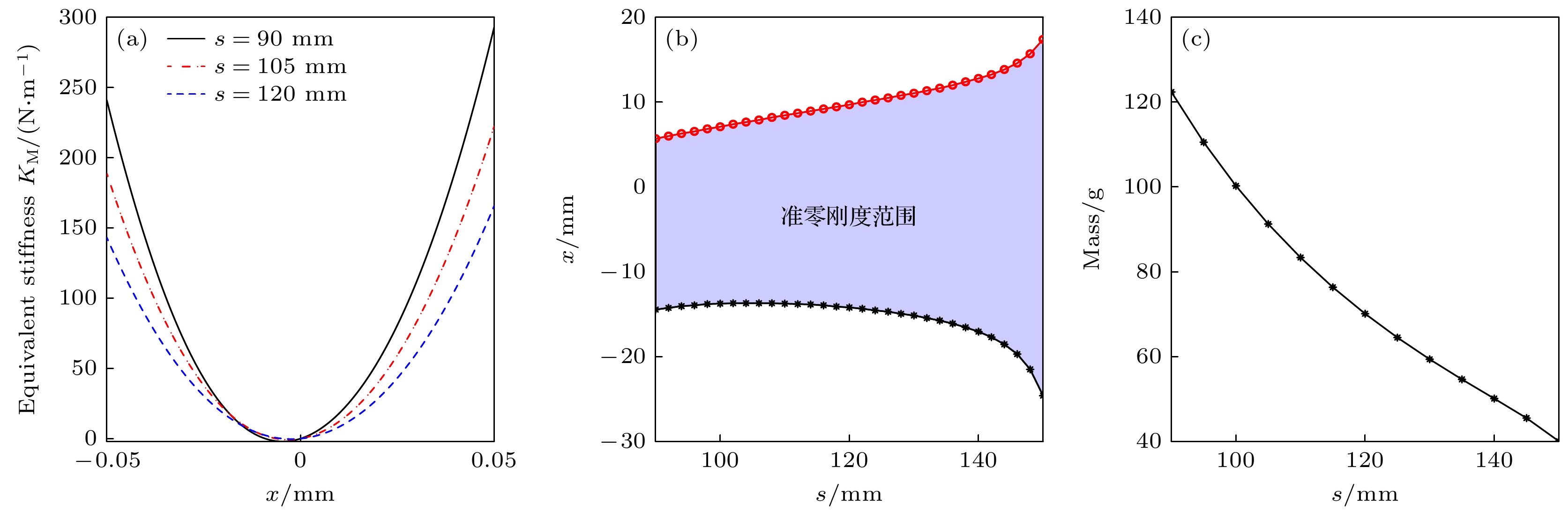
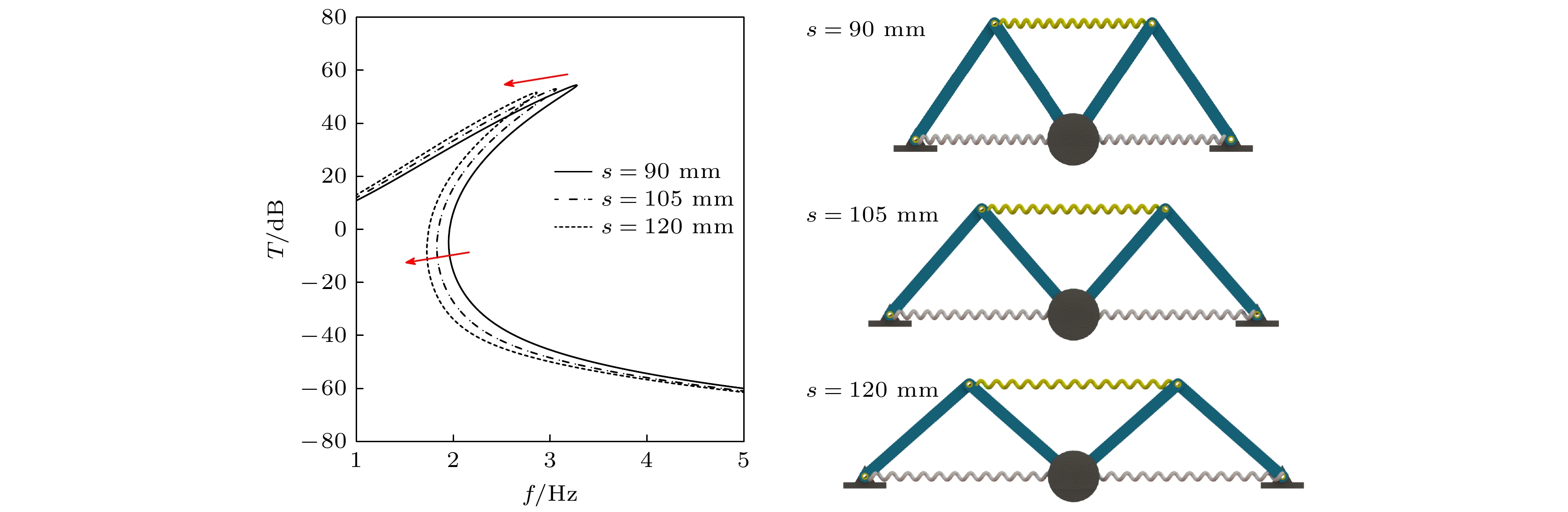
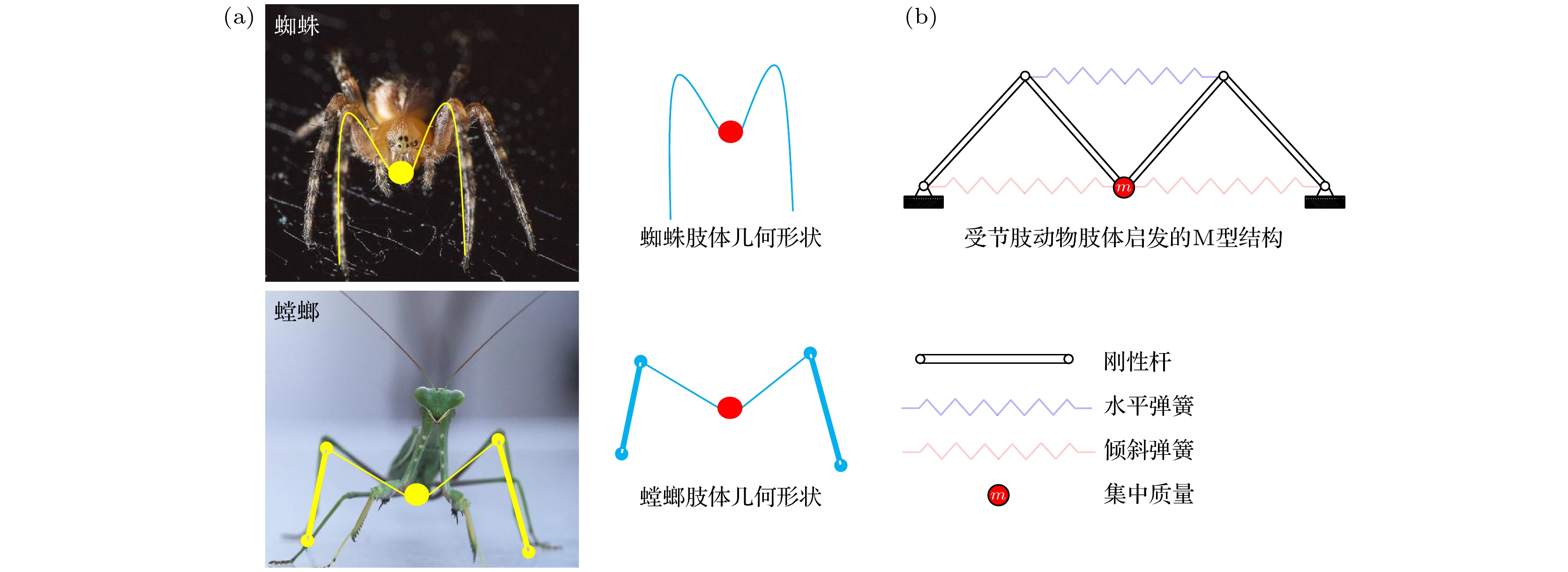
Arthropods, including spiders and mantises, are capable of maintaining their body stability on shaking surfaces, such as spiderwebs or leaves. This impressive stability can be attributed to the specific geometry of their limbs, which exhibit an M-shaped structure. Inspired by this geometry, this paper proposes an arthropod-limb-inspired M-shaped structure for low-frequency vibration isolation. First, the design methodology of the M-shaped quasi-zero-stiffness (QZS) structure is presented. A static analysis of potential energy, restoring force, and equivalent stiffness is conducted. It is revealed that the M-shaped structure enables a horizontal linear spring to generate nonlinear stiffness in the vertical direction. More importantly, this nonlinear stiffness effectively compensates for the negative stiffness in large-displacement responses, thereby achieving a wider quasi-zero-stiffness region compared to the conventional three-spring-based QZS structure. Subsequently, the harmonic balance method was employed to derive approximate analytical solutions for the M-shaped QZS structure, which were well validated through numerical simulation. A comparison between the proposed M-shaped QZS structure and the conventional three-spring-based QZS structure was performed. Results show that the M-shaped QZS structure is advantageous for reducing both the cut-in isolation frequency and the resonance frequency. In particular, under large excitation or small damping conditions, the performance improvement of the M-shaped QZS structure in terms of reducing the resonance frequency and maximum response becomes more pronounced. The underlying mechanism behind this feature is primarily attributed to the expanded QZS region induced by the M-shaped structure. Lastly, since the M-shaped structures vary among different arthropods, the effect of the geometry of M-shaped structures on low-frequency vibration performance was investigated. Interestingly, a trade-off between vibration isolation performance and loading mass was observed. As the M-shaped structure becomes flatter, the QZS region expands, and both the cut-in isolation frequency, the resonance frequency/peak, and the loading mass decrease. This occurs because a flatter M-shaped structure leads to a reduction in the equivalent stiffness generated by the horizontal stiffness. Consequently, while the loading mass capacity decreases, the low-frequency vibration isolation performance is enhanced. This novel finding provides a reasonable explanation for why most arthropods possess many pairs of limbs, allowing the loading mass to be distributed and enabling excellent low-frequency vibration isolation to be achieved simultaneously.