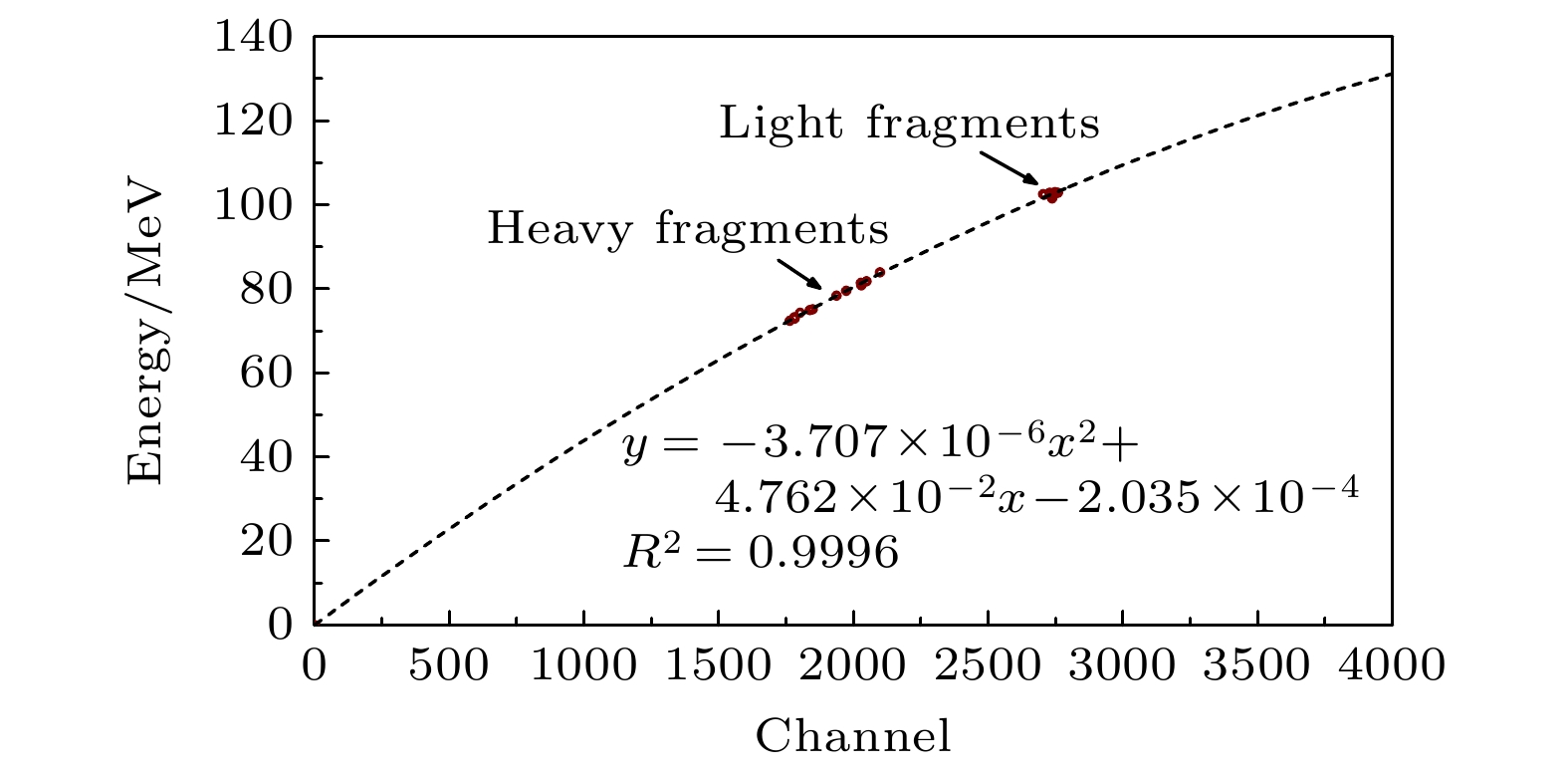
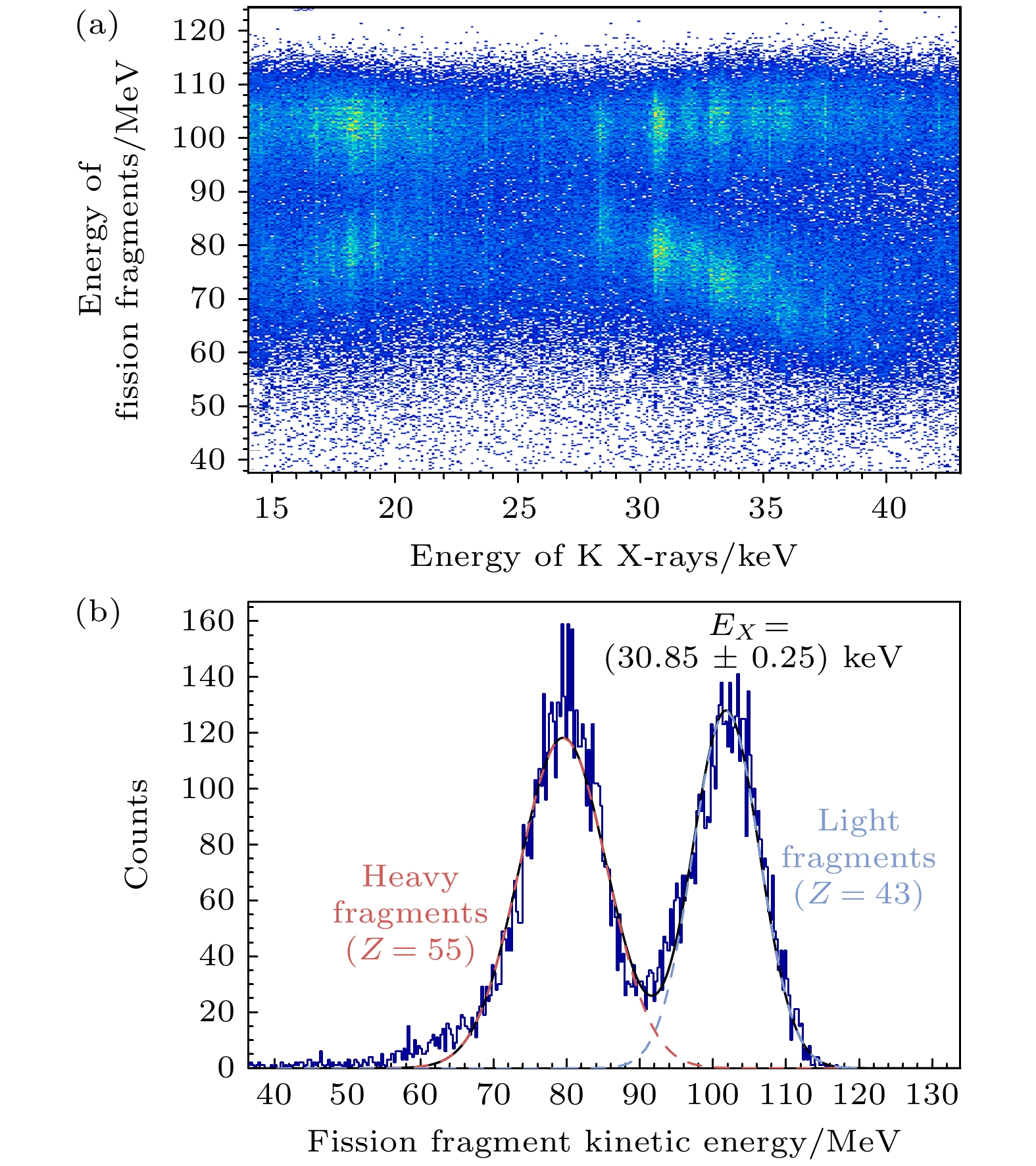
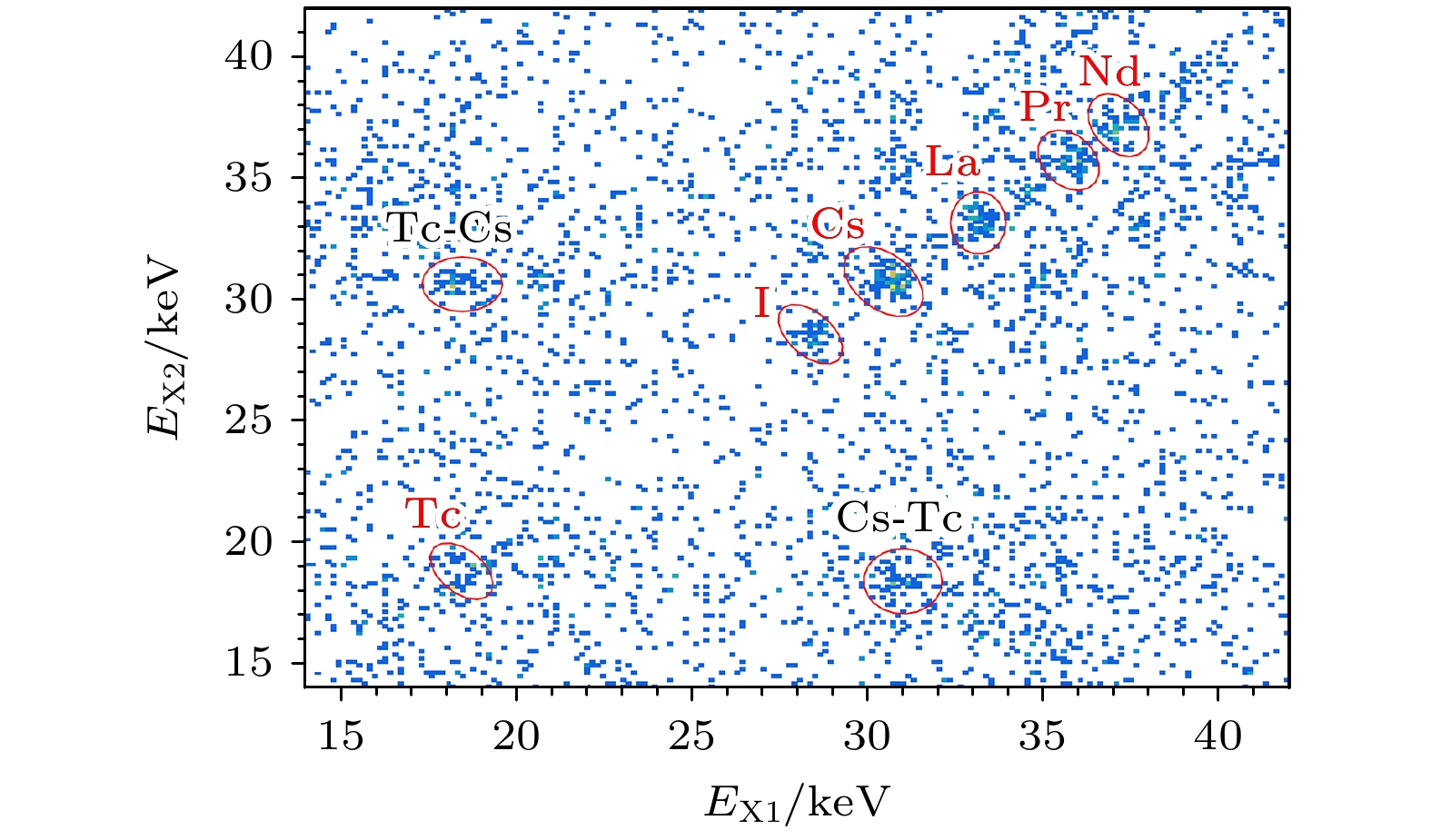
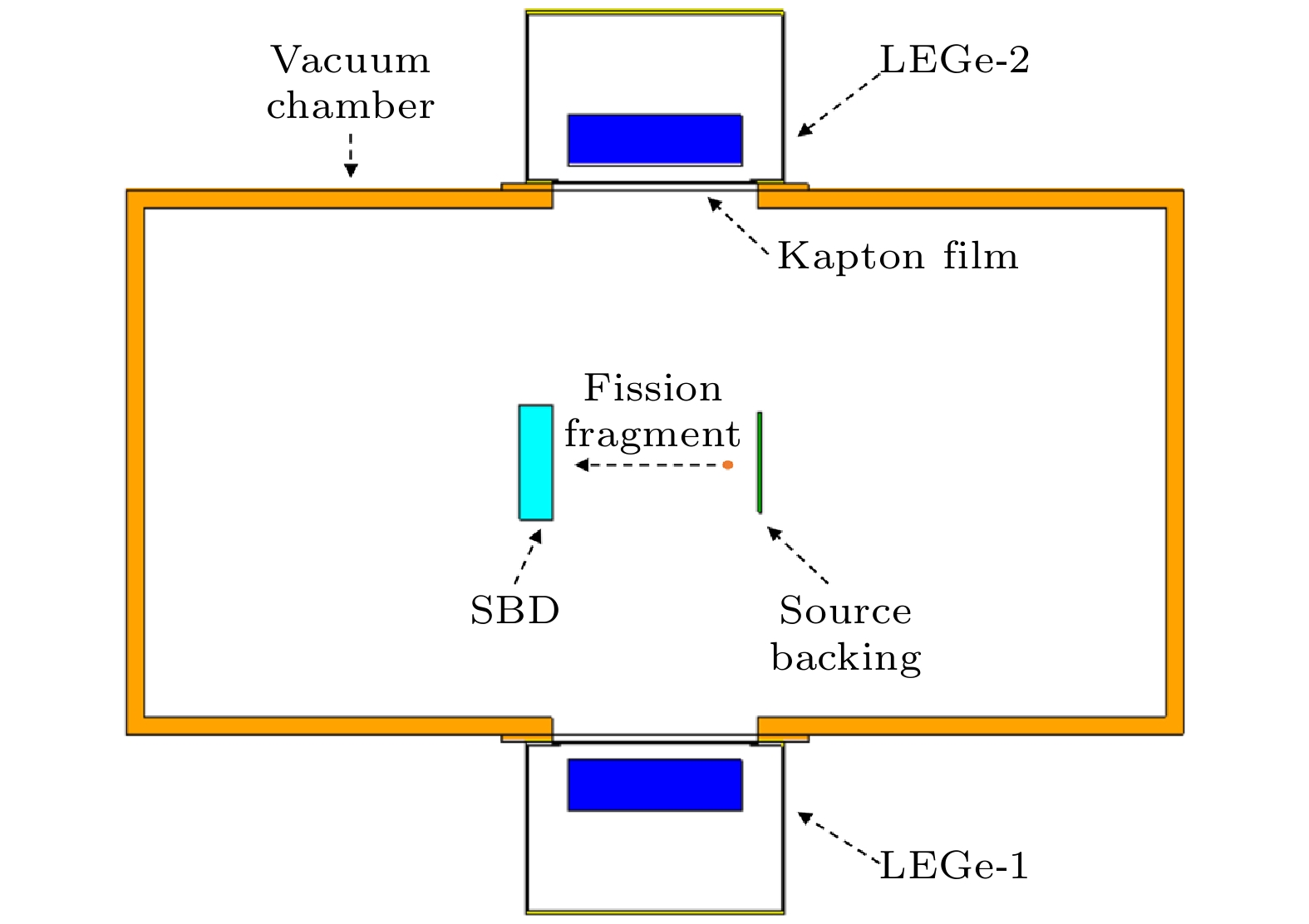
-
原子核裂变后多物理量间的关联测量是认识裂变过程直接有效的实验手段, 然而由于初级裂变产物准确的电荷鉴别仍面临技术困难, 电荷相关的多参数研究相对匮乏. 为此, 通过高分辨的低能高纯锗探测器和金硅面垒探测器开展了252Cf自发裂变的裂变碎片K X射线和动能的符合测量. 利用K X射线可以很好地鉴别电荷数Z = 39—62的裂变碎片, 电荷分辨ΔZ≈0.7, K X射线产额呈现强烈的电荷相关性. 借助K X射线给出了碎片平均动能和平均总动能及其分布宽度随核电荷数的分布, 轻碎片动能分布具有鲜明的奇偶效应, 偶Z碎片的动能比奇Z碎片的高约0.48 MeV; 平均总动能在Z = 52—53处达到峰值, 总动能分布宽度在Z = 56附近呈现凹坑, 这反映了形变壳结构对断点形状的显著影响. 裂变碎片K X射线发射的信息及动能-电荷关系研究可为裂变独立产额测量和裂变理论模型的检验提供必要的参考数据.Experimental study of physical quantities after fission provides crucial insights into the fission process, which is an indispensable way to test the fission theory. The characteristics of primary fission products before beta decay are of great value in unraveling fission kinematics and nuclear energy applications. However, the measurement of the fragment charge has always been challenging. Multi-parameter studies related to nuclear charge remain relatively scarce. The deexcitation of the primary fission products may undergo internal conversion and is often accompanied by characteristic X-ray emissions. Therefore, the correlated measurement of fragment kinetic energy and K X-rays for 252Cf spontaneous fission is conducted. A silicon surface barrier detector is used to measure the fragment kinetic energy, while two low-energy high-pure germanium detectors are utilized for K X-ray measurement. Identification of fission fragments with Z = 39–62 is realized through characteristic K X-rays with a charge resolution of ΔZ ≈ 0.7. Fission fragment K X-ray yields exhibit a strong charge correlation, with an odd-even effect factor of about 13%. Based on K X-rays, the post-neutron-emission average kinetic energy, average total kinetic energy
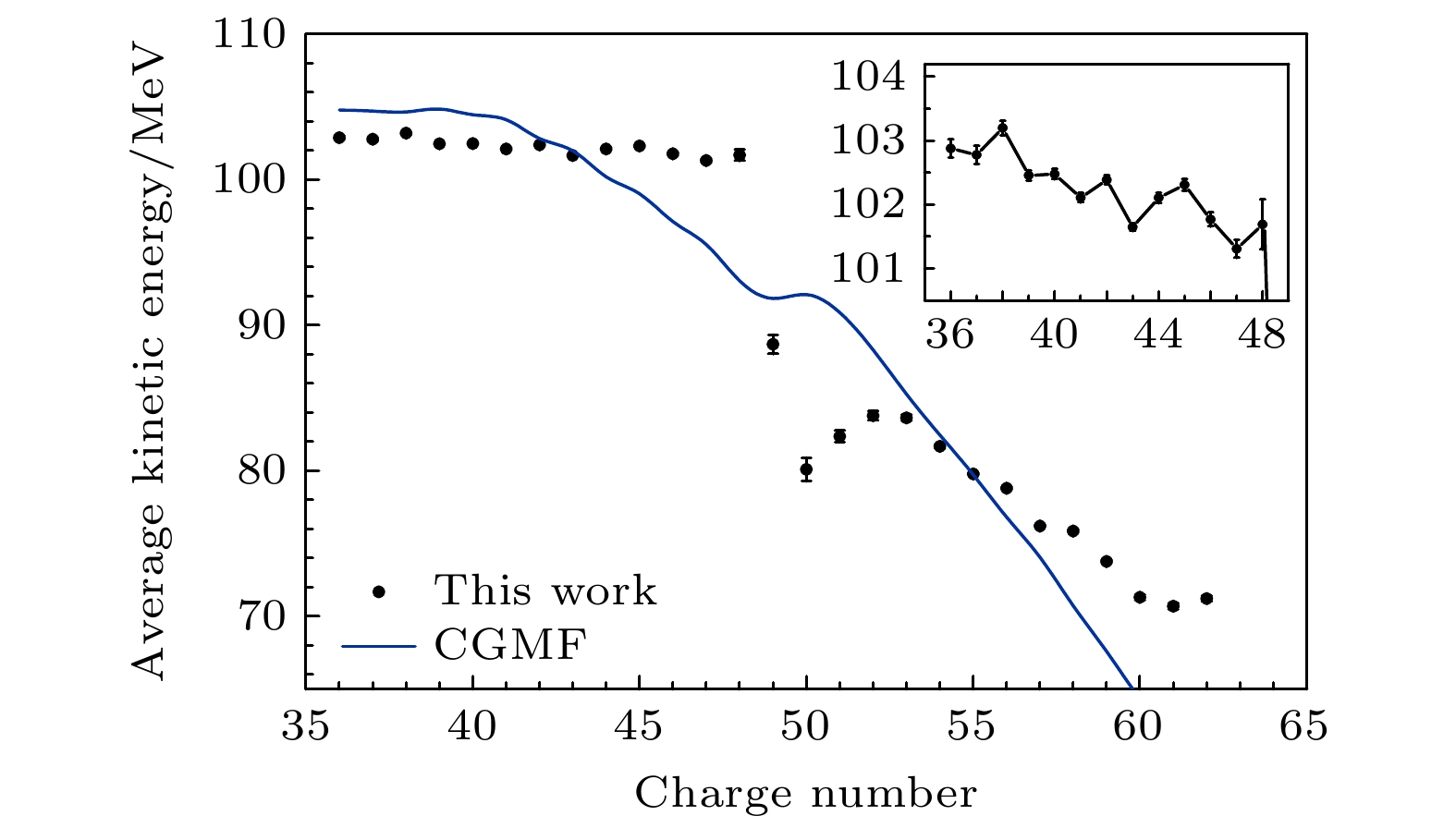
$(\langle \rm TKE\rangle) $ , and its dispersion ($ {\sigma }_{{\mathrm{T}}{\mathrm{K}}{\mathrm{E}}} $ ) of fission fragments are determined each as a function of nuclear charge. The kinetic energy distribution of light fragments shows a pronounced odd-even effect, with even-Z elements exhibiting kinetic energy enhanced by about 0.48 MeV compared with odd-Z fragments. The peak of the$(\langle\rm TKE\rangle) $ distribution is nearly Z = 52–53, while the minimum of the$ {\sigma }_{{\mathrm{T}}{\mathrm{K}}{\mathrm{E}}} $ appears near Z = 56, indicating the significant influence of deformed shells in the highly asymmetric fission region. The post-neutron kinetic energy distribution of fission fragments from 252Cf (sf) is calculated by using the GEF model and CGMF model. The CGMF model effectively reproduces the overall trend of kinetic energy as a function of charge number, while the results of the GEF calculation are systematically higher than the experimental values. Nonetheless, these two phenomenological models make it difficult to quantitatively describe the kinetic energy distribution of fission fragments accurately. In this study, the insights into K X-ray emissions and kinetic energy-nuclear charge relationships provide valuable reference data for independently measuring the fission yields and verifying the theoretical models of fission.-
Keywords:
- fission fragment /
- K X-ray /
- nuclear charge identification /
- fragment kinetic energy
[1] Lemaître J F, Goriely S, Hilaire S, Sida J L 2019 Phys. Rev. C 99 034612
Google Scholar
[2] Talou P, Stetcu I, Jaffke P, Rising M E, Lovell A E, Kawano T 2021 Comput. Phys. Commun. 269 108087
Google Scholar
[3] Scamps G, Simenel C 2018 Nature 564 382
Google Scholar
[4] Caamaño M, Farget F, Delaune O, Schmidt K H, Schmitt C, Audouin L, Bacri C O, Benlliure J, Casarejos E, Derkx X, Fernández-Domínguez B, Gaudefroy L, Golabek C, Jurado B, Lemasson A, Ramos D, Rodríguez-Tajes C, Roger T, Shrivastava A 2015 Phys. Rev. C 92 034606
Google Scholar
[5] Mariolopoulos G, Hamelin C, Blachot J, Bocquet J P, Brissot R, Crançon J, Nifenecker H, Ristori C 1981 Nucl. Phys. A 361 213
Google Scholar
[6] Lang W, Clerc H G, Wohlfarth H, Schrader H, Schmidt K H 1980 Nucl. Phys. A 345 34
Google Scholar
[7] Wang T F, Li G W, Zhu L P, Hen O, Zhang G L, Meng Q H, Wang L M, Han H Y, Xia H H 2017 Phys. Rev. C 96 034611
Google Scholar
[8] Knitter H H, Hambsch F J, Budtz-Jørgensen C 1992 Nucl. Phys. A 536 221
Google Scholar
[9] Boucheneb N, Asghar M, Barreau G, Doan T P, Leroux B, Sicre A, Geltenbort P, Oed A 1991 Nucl. Phys. A 535 77
Google Scholar
[10] Glendenin L E, Griffin H C 1965 Phys. Lett. 15 153
Google Scholar
[11] Kapoor S S, Bowman H R, Thompson S G 1965 Phys. Rev. 140 B1310
Google Scholar
[12] Reisdorf W, Unik J P, Griffin H C, Glendenin L E 1971 Nucl. Phys. A 177 337
Google Scholar
[13] Griffin H C 1990 J. Radioanal. Nucl. Chem. 142 279
Google Scholar
[14] Liu S L, Yang Y, Li X, Jiang W G, Han H Y, Zhang C L 2017 At. Energy Sci. Technol. 51 343 (in chinese) [刘世龙, 杨毅, 李霞, 姜文刚, 韩洪银, 张春利 2017 原子能科学技术 51 343]
Google Scholar
Liu S L, Yang Y, Li X, Jiang W G, Han H Y, Zhang C L 2017 At. Energy Sci. Technol. 51 343 (in chinese)
Google Scholar
[15] Algutifan N J, Sherman S R, Alexander C W 2015 Appl. Radiat. Isot. 96 135
Google Scholar
[16] Bé M M, Chechev V P, Dersch R, Helene O A, Helmer R G, Herman M, Hlaváč S, Marcinkowski A, Molnár G L, Nichols A L, Schönfeld E, Vanin V R, Woods M J 2007 Update of X-ray and Gamma-ray Decay Data Standards for Detector Calibration and Other Applications (Vol. 2) (Vienna: IAEA) p50
[17] Tovesson F, Hambsch F J, Oberstedt S, Bax H 2002 J. Nucl. Sci. Technol. 39 673
[18] Schmitt H W, Kiker W E, Williams C W 1965 Phys. Rev. 137 B837
Google Scholar
[19] Weissenberger E, Geltenbort P, Oed A, Gönnenwein F, Faust H 1986 Nucl. Instrum. Methods A 248 506
Google Scholar
[20] Waldo R W, Karam R A, Meyer R A 1981 Phys. Rev. C 23 1113
Google Scholar
[21] Schmidt K H, Jurado B, Amouroux C, Schmitt C 2016 Nucl. Data Sheets 131 107
Google Scholar
[22] Henschel H, Kohnle A, Hipp H, Gönnenwein G 1981 Nucl. Instrum. Methods 190 125
Google Scholar
[23] Rao M N, Biswas D C, Choudhury R K 1990 Nucl. Instrum. Methods B 51 102
Google Scholar
[24] Brown D A, Chadwick M B, Capote R, et al. 2018 Nucl. Data Sheets 148 1
Google Scholar
[25] Dolce S R, Gibson W M, Thomas T D 1969 Phys. Rev. 180 1177
Google Scholar
[26] Glendenin L E, Unik J P 1965 Phys. Rev. 140 B1301
Google Scholar
[27] Hopkins F F, White J R, Phillips G W, Moore C F, Richard P 1972 Phys. Rev. C 5 1015
Google Scholar
[28] Laurent R S, Phillips G W, Richard P, Moore C F 1971 Phys. Rev. C 4 1948
Google Scholar
[29] Hambsch F J, Oberstedt S 1997 Nucl. Phys. A 617 347
Google Scholar
[30] Böckstiegel C, Steinhäuser S, Schmidt K H, Clerc H G, Grewe A, Heinz A, de Jong M, Junghans A R, Müller J, Voss B 2008 Nucl. Phys. A 802 12
Google Scholar
[31] Chemey A, Pica A, Yao L, Loveland W, Lee H Y, Kuvin S A 2020 Eur. Phys. J. A 56 1
Google Scholar
-
图 1 裂变碎片与X射线符合测量装置示意图
Fig. 1. Schematic view of the experimental setup for fission fragment and X-ray correlated measurement.
图 2 低能高纯锗探测器的探测效率曲线
Fig. 2. Detection efficiency curve for the low energy germanium detector.
图 3 符合测量装置对X射线的绝对探测效率
Fig. 3. Absolute X-ray detection efficiency for the correlated measurement setup.
图 4 252Cf自发裂变的裂变碎片K X射线能谱
Fig. 4. Fission fragment K X-ray energy spectrum for 252Cf (sf).
图 5 金硅面垒半导体探测器对典型裂变碎片的能量响应
Fig. 5. Energy response of the silicon surface barrier detector for typical fission fragments.
图 6 252Cf自发裂变的放中子后裂变碎片能谱
Fig. 6. Kinetic energy distribution of the post-neutron fragment from 252Cf (sf).
图 7 (a)裂变碎片动能与K X射线能量二维谱; (b)依据K X射线能量开窗的碎片动能分布
Fig. 7. (a) Two-dimensional histogram for fission fragment kinetic energies and K X-rays; (b) fission fragment kinetic energy distribution gated by K X-ray energy.
图 8 252Cf自发裂变的K X射线相对产额与电荷数的关系
Fig. 8. K X-ray yields of fission fragments as a function of nuclear charge for 252Cf (sf).
图 9 252Cf自发裂变的平均每碎片K X射线产额与电荷数的关系
Fig. 9. Average K X-rays per fragment as a function of nuclear charge for 252Cf(sf).
图 10 裂变碎片的X射线-X射线二维谱
Fig. 10. Two-dimensional histogram of X-ray-X-ray for fission fragments.
图 11 252Cf自发裂变的放中子后裂变碎片平均动能与电荷的关系
Fig. 11. The post-neutron fragment average kinetic energy as a function of nuclear charge for 252Cf (sf).
图 12 252Cf自发裂变放中子后(a)平均总动能, (b)总动能分布宽度与裂变碎片电荷的关系
Fig. 12. The nuclear charge-dependent of (a) post-neutron TKE and (b) the variance of the TKE distributions for 252Cf (sf).
表 1 252Cf自发裂变的平均动能和平均总动能
Table 1. Average kinetic energy and average total kinetic energy of fission fragments for 252Cf (sf).
下载: 导出CSV
-
[1] Lemaître J F, Goriely S, Hilaire S, Sida J L 2019 Phys. Rev. C 99 034612
Google Scholar
[2] Talou P, Stetcu I, Jaffke P, Rising M E, Lovell A E, Kawano T 2021 Comput. Phys. Commun. 269 108087
Google Scholar
[3] Scamps G, Simenel C 2018 Nature 564 382
Google Scholar
[4] Caamaño M, Farget F, Delaune O, Schmidt K H, Schmitt C, Audouin L, Bacri C O, Benlliure J, Casarejos E, Derkx X, Fernández-Domínguez B, Gaudefroy L, Golabek C, Jurado B, Lemasson A, Ramos D, Rodríguez-Tajes C, Roger T, Shrivastava A 2015 Phys. Rev. C 92 034606
Google Scholar
[5] Mariolopoulos G, Hamelin C, Blachot J, Bocquet J P, Brissot R, Crançon J, Nifenecker H, Ristori C 1981 Nucl. Phys. A 361 213
Google Scholar
[6] Lang W, Clerc H G, Wohlfarth H, Schrader H, Schmidt K H 1980 Nucl. Phys. A 345 34
Google Scholar
[7] Wang T F, Li G W, Zhu L P, Hen O, Zhang G L, Meng Q H, Wang L M, Han H Y, Xia H H 2017 Phys. Rev. C 96 034611
Google Scholar
[8] Knitter H H, Hambsch F J, Budtz-Jørgensen C 1992 Nucl. Phys. A 536 221
Google Scholar
[9] Boucheneb N, Asghar M, Barreau G, Doan T P, Leroux B, Sicre A, Geltenbort P, Oed A 1991 Nucl. Phys. A 535 77
Google Scholar
[10] Glendenin L E, Griffin H C 1965 Phys. Lett. 15 153
Google Scholar
[11] Kapoor S S, Bowman H R, Thompson S G 1965 Phys. Rev. 140 B1310
Google Scholar
[12] Reisdorf W, Unik J P, Griffin H C, Glendenin L E 1971 Nucl. Phys. A 177 337
Google Scholar
[13] Griffin H C 1990 J. Radioanal. Nucl. Chem. 142 279
Google Scholar
[14] Liu S L, Yang Y, Li X, Jiang W G, Han H Y, Zhang C L 2017 At. Energy Sci. Technol. 51 343 (in chinese) [刘世龙, 杨毅, 李霞, 姜文刚, 韩洪银, 张春利 2017 原子能科学技术 51 343]
Google Scholar
Liu S L, Yang Y, Li X, Jiang W G, Han H Y, Zhang C L 2017 At. Energy Sci. Technol. 51 343 (in chinese)
Google Scholar
[15] Algutifan N J, Sherman S R, Alexander C W 2015 Appl. Radiat. Isot. 96 135
Google Scholar
[16] Bé M M, Chechev V P, Dersch R, Helene O A, Helmer R G, Herman M, Hlaváč S, Marcinkowski A, Molnár G L, Nichols A L, Schönfeld E, Vanin V R, Woods M J 2007 Update of X-ray and Gamma-ray Decay Data Standards for Detector Calibration and Other Applications (Vol. 2) (Vienna: IAEA) p50
[17] Tovesson F, Hambsch F J, Oberstedt S, Bax H 2002 J. Nucl. Sci. Technol. 39 673
[18] Schmitt H W, Kiker W E, Williams C W 1965 Phys. Rev. 137 B837
Google Scholar
[19] Weissenberger E, Geltenbort P, Oed A, Gönnenwein F, Faust H 1986 Nucl. Instrum. Methods A 248 506
Google Scholar
[20] Waldo R W, Karam R A, Meyer R A 1981 Phys. Rev. C 23 1113
Google Scholar
[21] Schmidt K H, Jurado B, Amouroux C, Schmitt C 2016 Nucl. Data Sheets 131 107
Google Scholar
[22] Henschel H, Kohnle A, Hipp H, Gönnenwein G 1981 Nucl. Instrum. Methods 190 125
Google Scholar
[23] Rao M N, Biswas D C, Choudhury R K 1990 Nucl. Instrum. Methods B 51 102
Google Scholar
[24] Brown D A, Chadwick M B, Capote R, et al. 2018 Nucl. Data Sheets 148 1
Google Scholar
[25] Dolce S R, Gibson W M, Thomas T D 1969 Phys. Rev. 180 1177
Google Scholar
[26] Glendenin L E, Unik J P 1965 Phys. Rev. 140 B1301
Google Scholar
[27] Hopkins F F, White J R, Phillips G W, Moore C F, Richard P 1972 Phys. Rev. C 5 1015
Google Scholar
[28] Laurent R S, Phillips G W, Richard P, Moore C F 1971 Phys. Rev. C 4 1948
Google Scholar
[29] Hambsch F J, Oberstedt S 1997 Nucl. Phys. A 617 347
Google Scholar
[30] Böckstiegel C, Steinhäuser S, Schmidt K H, Clerc H G, Grewe A, Heinz A, de Jong M, Junghans A R, Müller J, Voss B 2008 Nucl. Phys. A 802 12
Google Scholar
[31] Chemey A, Pica A, Yao L, Loveland W, Lee H Y, Kuvin S A 2020 Eur. Phys. J. A 56 1
Google Scholar
下载:
计量
- 文章访问数: 1328
- PDF下载量: 46
- 被引次数: 0
