哈勃常数危机

蔡荣根; 李理; 王少江

doi:10.7498/aps.72.20231270

摘要

哈勃常数定量刻画了当前宇宙的膨胀速率, 精确测定哈勃常数是现代宇宙学的一个重要科学问题. 近年来, 哈勃常数的局域直接测量值与全局模型拟合值之间出现了越来越严重的偏差, 其中局域直接测量值来自于晚期宇宙的局域距离阶梯测量结果, 而全局模型拟合值来自于早期宇宙的微波背景辐射对宇宙学标准模型的观测限制. 如果该偏差不是由其中任何一种观测手段的观测误差和系统误差所致, 那么很有可能意味着存在超出宇宙学标准模型的新物理. 本文从观测和模型两方面简述该哈勃常数危机问题, 并结合作者近年来对此问题的研究从观测和模型两方面进行展望.

关键词:

Abstract

The Hubble constant quantitatively characterizes the expansion rate of the current Universe, and its precise measurement has become a crucial scientific problem. In recent years, there has been an increasingly serious discrepancy between the local direct measurements of the Hubble constant and the global fitting results, where the local direct measurements come from the local distance ladder measurements of the late universe, and the global fitting results come from fitting the standard model of cosmology to the microwave background radiation from the early universe. If this discrepancy is not caused by the observation error and systematic error of any of the observation methods, it probably means that there is a new physics beyond the existing standard model of cosmology. This article briefly reviews the Hubble constant problem from two aspects with observational and theoretical points of view, and finally provide a perspective view from both observational and theoretical aspects by combining the author’s research on this problem in recent years. The observational review includes cosmological observations from both early Universe (either depending or independent of the CMB measurements) and late Universe (either depending or independent of the distant-ladder measurements), and the theoretical review includes model buildings from modifying both early Universe (either recombination history or expansion history) and late Universe (either homogeneous modifications or inhomogeneous modifications). The final observational perspective includes both local and non-local cosmic variances with their Hubble residual correlated to the matter density contrasts of observer and sample, respectively, and the final theoretical perspective concludes the interacting dark energy model as the most promising candidate for both Hubble tension and S₈ tension, which can be specifically realized in a chameleon dark energy model, pointing to a scale-dependent effective cosmological constant.

Keywords:

作者及机构信息

1.
宁波大学物理科学与技术学院, 宁波　315211

2.
中国科学院理论物理研究所, 北京　100190

3.
中国科学院大学物理科学学院, 北京　100049

4.
中国科学院大学杭州高等研究院, 杭州　310024

通信作者: 王少江, schwang@itp.ac.cn

基金项目: 国家重点研发计划(批准号: 2021YFA0718304, 2021YFC2203004, 2020YFC2201502)和国家自然科学基金(批准号: 12105344, 12235019, 11821505, 11991052, 11947302, 12122513) 资助的课题.

Authors and contacts

1.
School of Physical Science and Technology, Ningbo University, Ningbo 315211, China

2.
Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, China

3.
School of Physical Sciences, University of Chinese Academy of Sciences (UCAS), Beijing 100049, China

4.
Hangzhou Institute for Advanced Study (HIAS), University of Chinese Academy of Sciences (UCAS), Hangzhou 310024, China

Corresponding author: Wang Shao-Jiang, schwang@itp.ac.cn

Funds: Project supported by the National Key Research and Development Program of China (Grant Nos. 2021YFA0718304, 2021YFC2203004, 2020YFC2201502) and the National Natural Science Foundation of China (Grant Nos. 12105344, 12235019, 11821505, 11991052, 11947302, 12122513).

文章全文 : translate this paragraph

参考文献

[1]	Aghanim N, et al. 2020 Astron. Astrophys. 641 A6 [Erratum: 2021 Astron. Astrophys. 652 C4
[2]	Riess A G, et al. 2022 Astrophys. J. Lett. 934 L7 Google Scholar
[3]	Bernal J L, Verde L, Riess A G 2016 JCAP 1610 019 Google Scholar
[4]	Verde L, Treu T, Riess A G 2019 Nat. Astrono. 3 891 Google Scholar
[5]	Knox L, Millea M 2020 Phys. Rev. D 101 043533 Google Scholar
[6]	Riess A G 2019 Nat. Rev. Phys. 2 10 Google Scholar
[7]	Di Valentino E, et al. 2021 Astropart. Phys. 131 102605 Google Scholar
[8]	Di Valentino E, Mena O, Pan S, Visinelli L, Yang W, Melchiorri A, Mota D F, Riess A G, Silk J 2021 Classical Quantum Gravity 38 153001 Google Scholar
[9]	Perivolaropoulos L, Skara F 2022 New Astron. Rev. 95 101659 Google Scholar
[10]	Abdalla E, et al. 2022 JHEAp 34 49 Google Scholar
[11]	Schöneberg N, Franco Abellán G, Pérez Sánchez A, Witte S J, Poulin V, Lesgourgues J 2022 Phys. Rep. 984 1 Google Scholar
[12]	Jedamzik K, Pogosian L, Zhao G B 2021 Commun. Phys. 4 123 Google Scholar
[13]	Cai R G, Guo Z K, Wang S J, Yu W W, Zhou Y 2022 Phys. Rev. D 105 L021301 Google Scholar
[14]	Cai R G, Guo Z K, Wang S J, Yu W W, Zhou Y 2022 Phys. Rev. D 106 063519 Google Scholar
[15]	Hinshaw G, et al. 2013 Astrophys. J. Suppl. 208 19 Google Scholar
[16]	Dutcher D, et al. 2021 Phys. Rev. D 104 022003 Google Scholar
[17]	Aiola S, et al. 2020 JCAP 12 047 Google Scholar
[18]	Birrer S, et al. 2020 Astron. Astrophys. 643 A165 Google Scholar
[19]	Schöneberg N, Lesgourgues J, Hooper D C 2019 JCAP 1910 029 Google Scholar
[20]	Zhang X, Huang Q G 2019 Commun. Theor. Phys. 71 826 Google Scholar
[21]	Alam S, et al. 2021 Phys. Rev. D 103 083533 Google Scholar
[22]	Ivanov M M, Simonović M, Zaldarriaga M 2020 JCAP 05 042 Google Scholar
[23]	Philcox O H E, Ivanov M M, Simonović M, Zaldarriaga M 2020 JCAP 2005 032 Google Scholar
[24]	Zhang P, D’Amico G, Senatore L, Zhao C, Cai Y 2022 JCAP 02 036 Google Scholar
[25]	Pisanti O, Cirillo A, Esposito S, Iocco F, Mangano G, Miele G, Serpico P D 2008 Comput. Phys. Commun. 178 956 Google Scholar
[26]	Pitrou C, Coc A, Uzan J P, Vangioni E 2018 Phys. Rep. 754 1 Google Scholar
[27]	Dhawan S, Brout D, Scolnic D, Goobar A, Riess A G, Miranda V 2020 Astrophys. J. 894 54 Google Scholar
[28]	Freedman W L 2021 Astrophys. J. 919 16 Google Scholar
[29]	Khetan N, et al. 2021 Astron. Astrophys. 647 A72 Google Scholar
[30]	Huang C D, Riess A G, Yuan W, Macri L M, Zakamska N L, Casertano S, Whitelock P A, Hoffmann S L, Filippenko A V, Scolnic D 2020 Astrophys. J. 889 5 Google Scholar
[31]	Wong K C, et al. 2020 Mon. Not. R. Astron. Soc. 498 1420 Google Scholar
[32]	Shajib A J, et al. 2020 Mon. Not. R. Astron. Soc. 494 6072 Google Scholar
[33]	Schutz B F 1986 Nature 323 310 Google Scholar
[34]	Krolak A, Schutz B F 1987 Gen. Rel. Grav. 19 1163 Google Scholar
[35]	Sathyaprakash B S, Schutz B F 2009 Living Rev. Rel. 12 2 Google Scholar
[36]	Abbott B, et al. 2017 Phys. Rev. Lett. 119 161101 Google Scholar
[37]	Abbott B, et al. 2017 Nature 551 85 Google Scholar
[38]	Hotokezaka K, Nakar E, Gottlieb O, Nissanke S, Masuda K, Hallinan G, Mooley K P, Deller A T 2019 Nat. Astron. 3 940 Google Scholar
[39]	Mukherjee S, Lavaux G, Bouchet F R, Jasche J, Wandelt B D, Nissanke S M, Leclercq F, Hotokezaka K 2021 Astron. Astrophys. 646 A65 Google Scholar
[40]	Wang R, Ruan W H, Yang Q, Guo Z K, Cai R G, Hu B 2022 Natl. Sci. Rev. 9 nwab054 Google Scholar
[41]	Guo R Y, Zhang J F, Zhang X 2019 JCAP 02 054 Google Scholar
[42]	Okamatsu F, Sekiguchi T, Takahashi T 2021 Phys. Rev. D 104 023523 Google Scholar
[43]	Jedamzik K, Pogosian L 2020 Phys. Rev. Lett. 125 181302 Google Scholar
[44]	Chiang C T, Slosar A 2018 arXiv: 1811.03624 [astro-ph.CO
[45]	Vachaspati T 2021 Rept. Prog. Phys. 84 074901 Google Scholar
[46]	Thiele L, Guan Y, Hill J C, Kosowsky A, Spergel D N 2021 Phys. Rev. D 104 063535 Google Scholar
[47]	Galli S, Pogosian L, Jedamzik K, Balkenhol L 2022 Phys. Rev. D 105 023513 Google Scholar
[48]	Liu M, Huang Z, Luo X, Miao H, Singh N K, Huang L 2020 Sci. China Phys. Mech. Astron. 63 290405 Google Scholar
[49]	Hart L, Chluba J 2020 Mon. Not. R. Astron. Soc. 493 3255 Google Scholar
[50]	Sekiguchi T, Takahashi T 2021 Phys. Rev. D 103 083507 Google Scholar
[51]	Kreisch C D, Cyr-Racine F Y, Doré O 2020 Phys. Rev. D 101 123505 Google Scholar
[52]	Roy Choudhury S, Hannestad S, Tram T 2021 JCAP 03 084 Google Scholar
[53]	Poulin V, Smith T L, Karwal T, Kamionkowski M 2019 Phys. Rev. Lett. 122 221301 Google Scholar
[54]	Ye G, Piao Y S 2020 Phys. Rev. D 101 083507 Google Scholar
[55]	Cuesta A J, Verde L, Riess A, Jimenez R 2015 Mon. Not. Roy. Astron. Soc. 448 3463 Google Scholar
[56]	Heavens A, Jimenez R, Verde L 2014 Phys. Rev. Lett. 113 241302 Google Scholar
[57]	Aubourg E, et al. 2015 Phys. Rev. D 92 123516 Google Scholar
[58]	Vonlanthen M, Räsänen S, Durrer R 2010 JCAP 1008 023 Google Scholar
[59]	Aylor K, Joy M, Knox L, Millea M, Raghunathan S, Wu W L K 2019 Astrophys. J. 874 4 Google Scholar
[60]	Lemos P, Lee E, Efstathiou G, Gratton S 2019 Mon. Not. R. Astron. Soc. 483 4803 Google Scholar
[61]	Verde L, Bernal J L, Heavens A F, Jimenez R 2017 Mon. Not. R. Astron. Soc. 467 731 Google Scholar
[62]	Alam S, et al. 2017 Mon. Not. R. Astron. Soc. 470 2617 Google Scholar
[63]	Verde L, Bellini E, Pigozzo C, Heavens A F, Jimenez R 2017 JCAP 1704 023 Google Scholar
[64]	Macaulay E, et al. 2019 Mon. Not. R. Astron. Soc. 486 2184 Google Scholar
[65]	Feeney S M, Peiris H V, Williamson A R, Nissanke S M, Mortlock D J, Alsing J, Scolnic D 2019 Phys. Rev. Lett. 122 061105 Google Scholar
[66]	Taubenberger S, Suyu S H, Komatsu E, Jee I, Birrer S, Bonvin V, Courbin F, Rusu C E, Shajib A J, Wong K C 2019 Astron. Astrophys. 628 L7 Google Scholar
[67]	Arendse N, et al. 2020 Astron. Astrophys. 639 A57 Google Scholar
[68]	Zhang X, Huang Q G 2021 Phys. Rev. D 103 043513 Google Scholar
[69]	Mortonson M J, Hu W, Huterer D 2009 Phys. Rev. D 80 067301 Google Scholar
[70]	Benevento G, Hu W, Raveri M 2020 Phys. Rev. D 101 103517 Google Scholar
[71]	Camarena D, Marra V 2021 Mon. Not. R. Astron. Soc. 504 5164 Google Scholar
[72]	Efstathiou G 2021 Mon. Not. R. Astron. Soc. 505 3866 Google Scholar
[73]	Jimenez R, Loeb A 2002 Astrophys. J. 573 37 Google Scholar
[74]	Huang Z 2020 Astrophys. J. Lett. 892 L28 Google Scholar
[75]	Luo X, Huang Z, Qian Q, Huang L 2020 Astrophys. J. 905 53 Google Scholar
[76]	Huang L, Huang Z Q, Huang Z, Li Z Y, Li Z, Zhou H 2021 Res. Astron. Astrophys. 21 277 Google Scholar
[77]	Wang B, Abdalla E, Atrio-Barandela F, Pavon D 2016 Rep. Prog. Phys. 79 096901 Google Scholar
[78]	Di Valentino E, Melchiorri A, Mena O, Vagnozzi S 2020 Phys. Dark Univ. 30 100666 Google Scholar
[79]	Aluri P K, et al. 2023 Classical Quantum Gravity 40 094001 Google Scholar
[80]	Wu X P, Deng Z G, Zou Z L, Fang L Z, Qin B 1995 Astrophys. J. Lett. 448 L65 Google Scholar
[81]	Wu X P, Qin B, Fang L Z 1996 Astrophys. J. 469 48 Google Scholar
[82]	Lavaux G, Hudson M J 2011 Mon. Not. R. Astron. Soc. 416 2840 Google Scholar
[83]	Keenan R C, Barger A J, Cowie L L 2013 Astrophys. J. 775 62 Google Scholar
[84]	Hoscheit B L, Barger A J 2018 Astrophys. J. 854 46 Google Scholar
[85]	Kenworthy W D, Scolnic D, Riess A 2019 Astrophys. J. 875 145 Google Scholar
[86]	Luković V V, Haridasu B S, Vittorio N 2020 Mon. Not. R. Astron. Soc. 491 2075 Google Scholar
[87]	Cai R G, Ding J F, Guo Z K, Wang S J, Yu W W 2021 Phys. Rev. D 103 123539 Google Scholar
[88]	Cai R G, Guo Z K, Li L, Wang S J, Yu W W 2021 Phys. Rev. D 103 121302 Google Scholar
[89]	Yu W W, Li L, Wang S J 2022 arXiv: 2209.14732 [astro-ph.CO
[90]	Kelly P L, Hicken M, Burke D L, Mandel K S, Kirshner R P 2010 Astrophys. J. 715 743 Google Scholar
[91]	Sullivan M, et al. 2010 Mon. Not. R. Astron. Soc. 406 782 Google Scholar
[92]	Lampeitl H, et al. 2010 Astrophys. J. 722 566 Google Scholar
[93]	Gupta R R, et al. 2011 Astrophys. J. 740 92 [Erratum: 2011 Astrophys. J. 741 127
[94]	Johansson J, Thomas D, Pforr J, Maraston C, Nichol R C, Smith M, Lampeitl H, Beifiori A, Gupta R R, Schneider D P 2013 Mon. Not. R. Astron. Soc. 435 1680 Google Scholar
[95]	Childress M J, et al. 2013 Astrophys. J. 770 108 Google Scholar
[96]	Sheth R K, Diaferio A 2001 Mon. Not. R. Astron. Soc. 322 901 Google Scholar
[97]	Turner E L, Cen R, Ostriker J P 1992 Astron. J. 103 1427 Google Scholar
[98]	Camarena D, Marra V 2018 Phys. Rev. D 98 023537 Google Scholar
[99]	Wang Q 2020 Phys. Rev. Lett. 125 051301 Google Scholar

施引文献

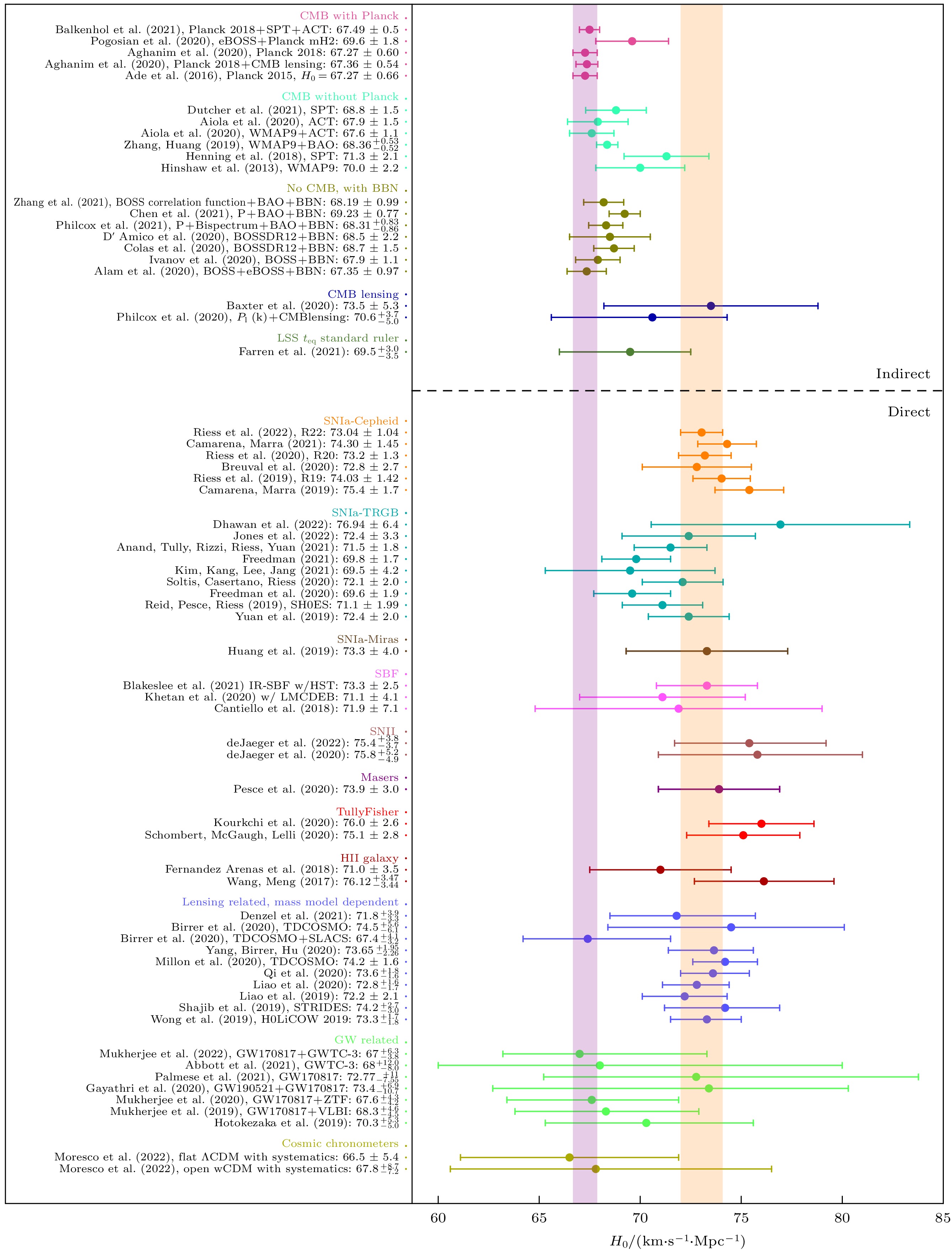
图 1 哈勃常数危机: 来自 CMB-Planck+$ \Lambda{\mathrm{CDM}} $的$ H_0 $限制(蓝色)与来自 SH0ES 合作组距离阶梯 SNe+Cepheid 的$ H_0 $测量(绿色)之间高达将近$ 5\sigma $的偏离. 图片来自文献[2]

Fig. 1. The Hubble-constant tension: The nearly$ 5\sigma $discrepancy between the$ H_0 $constraint (blue) from CMB-Planck+$ \Lambda{\mathrm{CDM}}$ and the$ H_0 $measurement (green) from SH0ES group using the distance ladder SNe+Cepheid. The figure comes from Ref. [2].

下载: 全尺寸图片幻灯片

图 2 哈勃常数危机: 来自早期宇宙的间接拟合和晚期宇宙的直接测量. 图片来自文献[8]

Fig. 2. The Hubble-constant tension: The indirect constraints from fitting the early Universe and direct measurements from the late Universe. The figure comes from Ref. [8].

下载: 全尺寸图片幻灯片

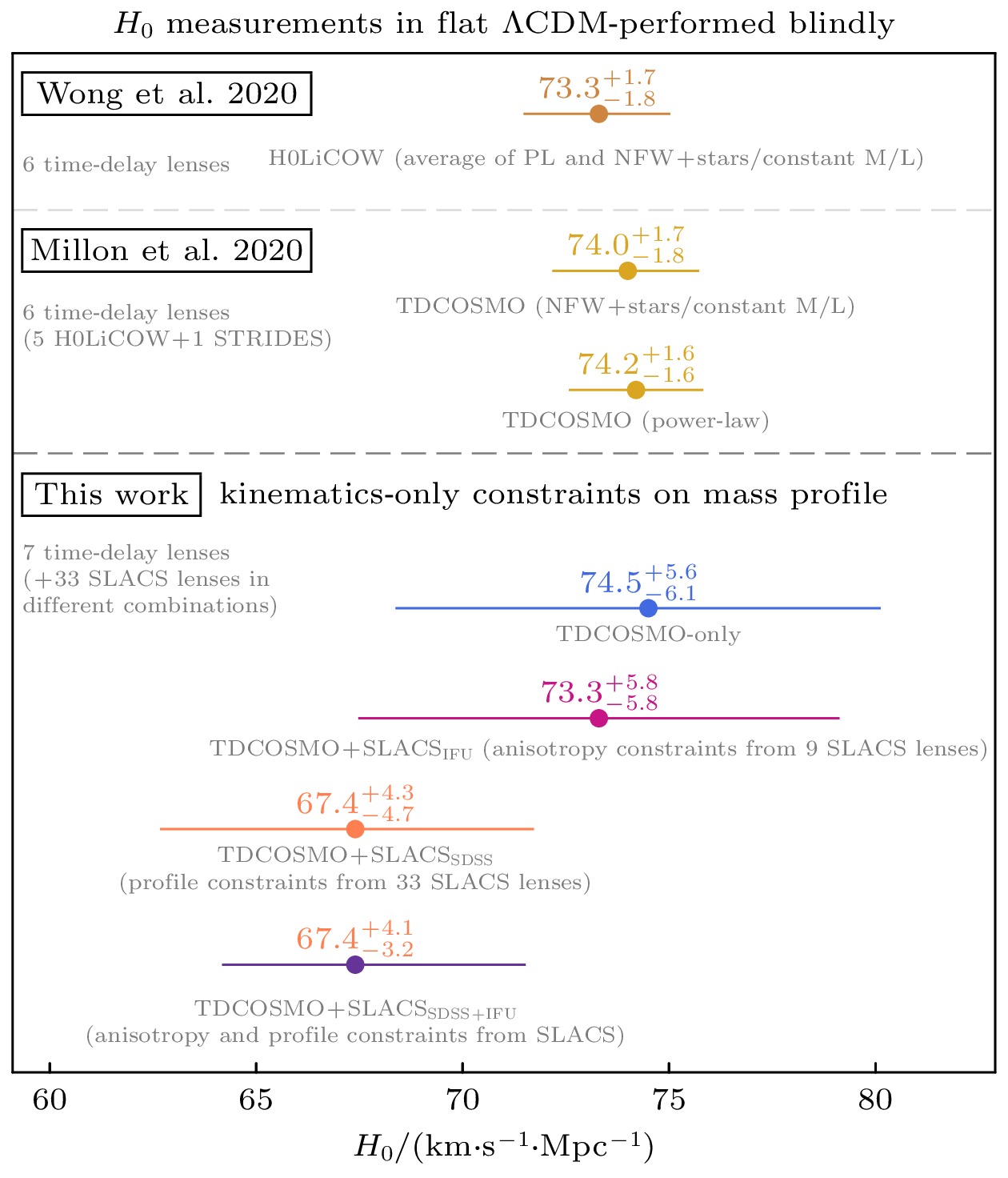
图 3 把BBN与星系BAO(蓝色)和Lyman-$ \alpha $BAO(绿色)结合后给出的限制(红色)与Planck 2018 限制结果(紫色)和SH0ES组测量结果(橙色)的对比. 图片来自文献[18]

Fig. 3. The comparison to the Planck 2018 constraint (purple) and the SH0ES measurement (orange) with respect to the joint constraint (red) from combing BBN with galaxy BAO (blue) and Lyman-$ \alpha $BAO (green). The figure comes from Ref. [18].

下载: 全尺寸图片幻灯片

图 4 SH0ES 合作组采用的三级距离阶梯. 图片来自文献[2]

Fig. 4. The three-rung distance ladder adopted by the SH0ES group. The figure comes from Ref. [2].

下载: 全尺寸图片幻灯片

图 5 来自与距离阶梯无关的强引力透镜时间延迟对哈勃常数测量, 图片来自文献[18]

Fig. 5. The Hubble-constant measurements from strong lensing time delay independent of distance ladders. The figure comes from Ref. [18].

下载: 全尺寸图片幻灯片

图 6 来自 LISA 和太极空间引力波探测器联网的对哈勃常数的暗汽笛限制. 图片来自文献[40]

Fig. 6. The dark siren constraints on the Hubble constant from the LISA-Taiji network. The figure comes from Ref. [40]

下载: 全尺寸图片幻灯片

图 7 星系弱引力透镜观测(左上)、SH0ES组对$ H_0 $的测量(左中)以及重子声学振荡观测(左下)对早期宇宙模型(右)的限制. 图片来自文献[12]

Fig. 7. The constraints (left) on the early-Universe models (right) from the galactic weak lensing observation (left top), the SH0ES measurement on$ H_0 $(left medium), and the BAO observation (left bottom). The figure comes from Ref. [12].

下载: 全尺寸图片幻灯片

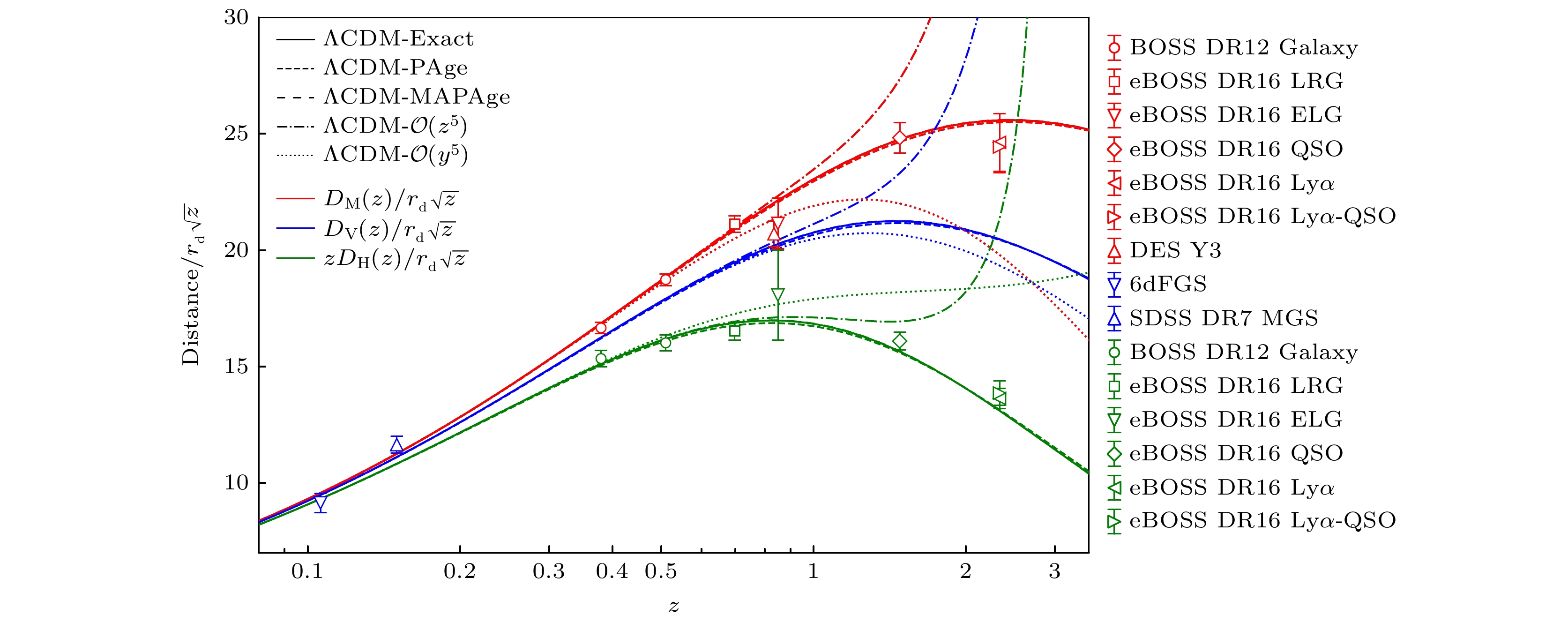
图 8 在$ \Lambda{\mathrm{CDM}} $ 模型及其PAge/MAPAge参数化模型以及按红移$ z $和$ y = 1 - a $的泰勒展开近似下的BAO特征尺度(红、蓝、绿)与BAO观测数据的对比. 图片来自文献[14]

Fig. 8. The comparison of characteristic BAO length scales to the BAO data from the$ \Lambda {\mathrm{CDM}}$ model and its PAge/MAPAge parameterization models as well as its Taylor expansion models in redshift$ z $and$ y=1-a $. The figure comes from Ref. [14].

下载: 全尺寸图片幻灯片

图 9 变色龙暗能量机制示意图　(a) 变色龙暗能量有效势$ V_{\rm{eff}}(\varphi) = V(\varphi) + U(\varphi) $, 其中变色龙场势函数取 Peebles-Ratra 势函数$ V(\varphi) = \alpha\varLambda^4(\varLambda/\varphi)^n $, 变色龙耦合项取伸缩子耦合$ U(\varphi) = \exp(\varphi/\varLambda)\hat{\rho}_{\rm{m}} $. 易见当实线对应的物质密度$ \hat{\rho}_{\rm{m}} $大于虚线对应的物质密度时, 相应地实线在有效势的真空期望值处对应的势函数值(真空能)也大于虚线的情况. (b) 选取 Planck 2018 测量结果(红色)为背景宇宙学, 那么局域物质密度超出(纵轴)对应的局域哈勃常数(横轴)可以拟合 SH0ES 测量结果(蓝色). 图片来自文献[88]

Fig. 9. The illustrative demonstration of the chameleon dark energy model. (a) The effective potential of chameleon dark energy is$ V_{\rm{eff}}(\varphi) = V(\varphi) + U(\varphi) $, where the chameleon potential is of Peebles-Ratra form$ V(\varphi) = \alpha\varLambda^4(\varLambda/\varphi)^n $, and the chameleon coupling is of dilaton form$ U(\varphi) = \exp(\varphi/\varLambda)\hat{\rho}_{\rm{m}} $. It is easy to see that when the solid curve corresponds to higher matter density$ \hat{\rho}_{\rm{m}} $than the dashed curve with lower one, then the potential energy (vacuum energy) at the vacuum expectation value of the effective potential is also higher than the dashed case. (b) Choosing the Planck 2018 result (red) as the background cosmology, then the corresponding local Hubble constant (horizontal axis) from given local matter density contrast (vertical axis) could fit the SH0ES result (blue). The figure comes from Ref. [88].

下载: 全尺寸图片幻灯片

map

[1]	Aghanim N, et al. 2020 Astron. Astrophys. 641 A6 [Erratum: 2021 Astron. Astrophys. 652 C4
[2]	Riess A G, et al. 2022 Astrophys. J. Lett. 934 L7 Google Scholar
[3]	Bernal J L, Verde L, Riess A G 2016 JCAP 1610 019 Google Scholar
[4]	Verde L, Treu T, Riess A G 2019 Nat. Astrono. 3 891 Google Scholar
[5]	Knox L, Millea M 2020 Phys. Rev. D 101 043533 Google Scholar
[6]	Riess A G 2019 Nat. Rev. Phys. 2 10 Google Scholar
[7]	Di Valentino E, et al. 2021 Astropart. Phys. 131 102605 Google Scholar
[8]	Di Valentino E, Mena O, Pan S, Visinelli L, Yang W, Melchiorri A, Mota D F, Riess A G, Silk J 2021 Classical Quantum Gravity 38 153001 Google Scholar
[9]	Perivolaropoulos L, Skara F 2022 New Astron. Rev. 95 101659 Google Scholar
[10]	Abdalla E, et al. 2022 JHEAp 34 49 Google Scholar
[11]	Schöneberg N, Franco Abellán G, Pérez Sánchez A, Witte S J, Poulin V, Lesgourgues J 2022 Phys. Rep. 984 1 Google Scholar
[12]	Jedamzik K, Pogosian L, Zhao G B 2021 Commun. Phys. 4 123 Google Scholar
[13]	Cai R G, Guo Z K, Wang S J, Yu W W, Zhou Y 2022 Phys. Rev. D 105 L021301 Google Scholar
[14]	Cai R G, Guo Z K, Wang S J, Yu W W, Zhou Y 2022 Phys. Rev. D 106 063519 Google Scholar
[15]	Hinshaw G, et al. 2013 Astrophys. J. Suppl. 208 19 Google Scholar
[16]	Dutcher D, et al. 2021 Phys. Rev. D 104 022003 Google Scholar
[17]	Aiola S, et al. 2020 JCAP 12 047 Google Scholar
[18]	Birrer S, et al. 2020 Astron. Astrophys. 643 A165 Google Scholar
[19]	Schöneberg N, Lesgourgues J, Hooper D C 2019 JCAP 1910 029 Google Scholar
[20]	Zhang X, Huang Q G 2019 Commun. Theor. Phys. 71 826 Google Scholar
[21]	Alam S, et al. 2021 Phys. Rev. D 103 083533 Google Scholar
[22]	Ivanov M M, Simonović M, Zaldarriaga M 2020 JCAP 05 042 Google Scholar
[23]	Philcox O H E, Ivanov M M, Simonović M, Zaldarriaga M 2020 JCAP 2005 032 Google Scholar
[24]	Zhang P, D’Amico G, Senatore L, Zhao C, Cai Y 2022 JCAP 02 036 Google Scholar
[25]	Pisanti O, Cirillo A, Esposito S, Iocco F, Mangano G, Miele G, Serpico P D 2008 Comput. Phys. Commun. 178 956 Google Scholar
[26]	Pitrou C, Coc A, Uzan J P, Vangioni E 2018 Phys. Rep. 754 1 Google Scholar
[27]	Dhawan S, Brout D, Scolnic D, Goobar A, Riess A G, Miranda V 2020 Astrophys. J. 894 54 Google Scholar
[28]	Freedman W L 2021 Astrophys. J. 919 16 Google Scholar
[29]	Khetan N, et al. 2021 Astron. Astrophys. 647 A72 Google Scholar
[30]	Huang C D, Riess A G, Yuan W, Macri L M, Zakamska N L, Casertano S, Whitelock P A, Hoffmann S L, Filippenko A V, Scolnic D 2020 Astrophys. J. 889 5 Google Scholar
[31]	Wong K C, et al. 2020 Mon. Not. R. Astron. Soc. 498 1420 Google Scholar
[32]	Shajib A J, et al. 2020 Mon. Not. R. Astron. Soc. 494 6072 Google Scholar
[33]	Schutz B F 1986 Nature 323 310 Google Scholar
[34]	Krolak A, Schutz B F 1987 Gen. Rel. Grav. 19 1163 Google Scholar
[35]	Sathyaprakash B S, Schutz B F 2009 Living Rev. Rel. 12 2 Google Scholar
[36]	Abbott B, et al. 2017 Phys. Rev. Lett. 119 161101 Google Scholar
[37]	Abbott B, et al. 2017 Nature 551 85 Google Scholar
[38]	Hotokezaka K, Nakar E, Gottlieb O, Nissanke S, Masuda K, Hallinan G, Mooley K P, Deller A T 2019 Nat. Astron. 3 940 Google Scholar
[39]	Mukherjee S, Lavaux G, Bouchet F R, Jasche J, Wandelt B D, Nissanke S M, Leclercq F, Hotokezaka K 2021 Astron. Astrophys. 646 A65 Google Scholar
[40]	Wang R, Ruan W H, Yang Q, Guo Z K, Cai R G, Hu B 2022 Natl. Sci. Rev. 9 nwab054 Google Scholar
[41]	Guo R Y, Zhang J F, Zhang X 2019 JCAP 02 054 Google Scholar
[42]	Okamatsu F, Sekiguchi T, Takahashi T 2021 Phys. Rev. D 104 023523 Google Scholar
[43]	Jedamzik K, Pogosian L 2020 Phys. Rev. Lett. 125 181302 Google Scholar
[44]	Chiang C T, Slosar A 2018 arXiv: 1811.03624 [astro-ph.CO
[45]	Vachaspati T 2021 Rept. Prog. Phys. 84 074901 Google Scholar
[46]	Thiele L, Guan Y, Hill J C, Kosowsky A, Spergel D N 2021 Phys. Rev. D 104 063535 Google Scholar
[47]	Galli S, Pogosian L, Jedamzik K, Balkenhol L 2022 Phys. Rev. D 105 023513 Google Scholar
[48]	Liu M, Huang Z, Luo X, Miao H, Singh N K, Huang L 2020 Sci. China Phys. Mech. Astron. 63 290405 Google Scholar
[49]	Hart L, Chluba J 2020 Mon. Not. R. Astron. Soc. 493 3255 Google Scholar
[50]	Sekiguchi T, Takahashi T 2021 Phys. Rev. D 103 083507 Google Scholar
[51]	Kreisch C D, Cyr-Racine F Y, Doré O 2020 Phys. Rev. D 101 123505 Google Scholar
[52]	Roy Choudhury S, Hannestad S, Tram T 2021 JCAP 03 084 Google Scholar
[53]	Poulin V, Smith T L, Karwal T, Kamionkowski M 2019 Phys. Rev. Lett. 122 221301 Google Scholar
[54]	Ye G, Piao Y S 2020 Phys. Rev. D 101 083507 Google Scholar
[55]	Cuesta A J, Verde L, Riess A, Jimenez R 2015 Mon. Not. Roy. Astron. Soc. 448 3463 Google Scholar
[56]	Heavens A, Jimenez R, Verde L 2014 Phys. Rev. Lett. 113 241302 Google Scholar
[57]	Aubourg E, et al. 2015 Phys. Rev. D 92 123516 Google Scholar
[58]	Vonlanthen M, Räsänen S, Durrer R 2010 JCAP 1008 023 Google Scholar
[59]	Aylor K, Joy M, Knox L, Millea M, Raghunathan S, Wu W L K 2019 Astrophys. J. 874 4 Google Scholar
[60]	Lemos P, Lee E, Efstathiou G, Gratton S 2019 Mon. Not. R. Astron. Soc. 483 4803 Google Scholar
[61]	Verde L, Bernal J L, Heavens A F, Jimenez R 2017 Mon. Not. R. Astron. Soc. 467 731 Google Scholar
[62]	Alam S, et al. 2017 Mon. Not. R. Astron. Soc. 470 2617 Google Scholar
[63]	Verde L, Bellini E, Pigozzo C, Heavens A F, Jimenez R 2017 JCAP 1704 023 Google Scholar
[64]	Macaulay E, et al. 2019 Mon. Not. R. Astron. Soc. 486 2184 Google Scholar
[65]	Feeney S M, Peiris H V, Williamson A R, Nissanke S M, Mortlock D J, Alsing J, Scolnic D 2019 Phys. Rev. Lett. 122 061105 Google Scholar
[66]	Taubenberger S, Suyu S H, Komatsu E, Jee I, Birrer S, Bonvin V, Courbin F, Rusu C E, Shajib A J, Wong K C 2019 Astron. Astrophys. 628 L7 Google Scholar
[67]	Arendse N, et al. 2020 Astron. Astrophys. 639 A57 Google Scholar
[68]	Zhang X, Huang Q G 2021 Phys. Rev. D 103 043513 Google Scholar
[69]	Mortonson M J, Hu W, Huterer D 2009 Phys. Rev. D 80 067301 Google Scholar
[70]	Benevento G, Hu W, Raveri M 2020 Phys. Rev. D 101 103517 Google Scholar
[71]	Camarena D, Marra V 2021 Mon. Not. R. Astron. Soc. 504 5164 Google Scholar
[72]	Efstathiou G 2021 Mon. Not. R. Astron. Soc. 505 3866 Google Scholar
[73]	Jimenez R, Loeb A 2002 Astrophys. J. 573 37 Google Scholar
[74]	Huang Z 2020 Astrophys. J. Lett. 892 L28 Google Scholar
[75]	Luo X, Huang Z, Qian Q, Huang L 2020 Astrophys. J. 905 53 Google Scholar
[76]	Huang L, Huang Z Q, Huang Z, Li Z Y, Li Z, Zhou H 2021 Res. Astron. Astrophys. 21 277 Google Scholar
[77]	Wang B, Abdalla E, Atrio-Barandela F, Pavon D 2016 Rep. Prog. Phys. 79 096901 Google Scholar
[78]	Di Valentino E, Melchiorri A, Mena O, Vagnozzi S 2020 Phys. Dark Univ. 30 100666 Google Scholar
[79]	Aluri P K, et al. 2023 Classical Quantum Gravity 40 094001 Google Scholar
[80]	Wu X P, Deng Z G, Zou Z L, Fang L Z, Qin B 1995 Astrophys. J. Lett. 448 L65 Google Scholar
[81]	Wu X P, Qin B, Fang L Z 1996 Astrophys. J. 469 48 Google Scholar
[82]	Lavaux G, Hudson M J 2011 Mon. Not. R. Astron. Soc. 416 2840 Google Scholar
[83]	Keenan R C, Barger A J, Cowie L L 2013 Astrophys. J. 775 62 Google Scholar
[84]	Hoscheit B L, Barger A J 2018 Astrophys. J. 854 46 Google Scholar
[85]	Kenworthy W D, Scolnic D, Riess A 2019 Astrophys. J. 875 145 Google Scholar
[86]	Luković V V, Haridasu B S, Vittorio N 2020 Mon. Not. R. Astron. Soc. 491 2075 Google Scholar
[87]	Cai R G, Ding J F, Guo Z K, Wang S J, Yu W W 2021 Phys. Rev. D 103 123539 Google Scholar
[88]	Cai R G, Guo Z K, Li L, Wang S J, Yu W W 2021 Phys. Rev. D 103 121302 Google Scholar
[89]	Yu W W, Li L, Wang S J 2022 arXiv: 2209.14732 [astro-ph.CO
[90]	Kelly P L, Hicken M, Burke D L, Mandel K S, Kirshner R P 2010 Astrophys. J. 715 743 Google Scholar
[91]	Sullivan M, et al. 2010 Mon. Not. R. Astron. Soc. 406 782 Google Scholar
[92]	Lampeitl H, et al. 2010 Astrophys. J. 722 566 Google Scholar
[93]	Gupta R R, et al. 2011 Astrophys. J. 740 92 [Erratum: 2011 Astrophys. J. 741 127
[94]	Johansson J, Thomas D, Pforr J, Maraston C, Nichol R C, Smith M, Lampeitl H, Beifiori A, Gupta R R, Schneider D P 2013 Mon. Not. R. Astron. Soc. 435 1680 Google Scholar
[95]	Childress M J, et al. 2013 Astrophys. J. 770 108 Google Scholar
[96]	Sheth R K, Diaferio A 2001 Mon. Not. R. Astron. Soc. 322 901 Google Scholar
[97]	Turner E L, Cen R, Ostriker J P 1992 Astron. J. 103 1427 Google Scholar
[98]	Camarena D, Marra V 2018 Phys. Rev. D 98 023537 Google Scholar
[99]	Wang Q 2020 Phys. Rev. Lett. 125 051301 Google Scholar

[1]	要佳敏, 庄伟, 冯金扬, 王启宇, 赵阳, 王少凯, 吴书清, 李天初. 固定相位振动噪声对绝对重力测量的影响. , 2021, 70(21): 219101. doi: 10.7498/aps.70.20210884
[2]	王灿灿. 量子纠缠与宇宙学弗里德曼方程. , 2018, 67(17): 179501. doi: 10.7498/aps.67.20180813
[3]	窦健泰, 高志山, 马骏, 袁操今, 杨忠明. 基于图像信息熵的ptychography轴向距离误差校正. , 2017, 66(16): 164203. doi: 10.7498/aps.66.164203
[4]	易洪, 李松, 马跃, 黄科, 周辉, 史光远. 基于足印探测的激光测高仪在轨标定. , 2017, 66(13): 134206. doi: 10.7498/aps.66.134206
[5]	卢道明. 等距离耦合腔系统中的非局域性. , 2016, 65(10): 100301. doi: 10.7498/aps.65.100301
[6]	司铁岩, 袁军华, 吴艺林, 唐建新. 细菌运动中的物理生物学. , 2016, 65(17): 178703. doi: 10.7498/aps.65.178703
[7]	杨锦辉, 宋君强. 混沌系统模型误差平均绝对误差增长过程研究. , 2012, 61(22): 220510. doi: 10.7498/aps.61.220510
[8]	周庆, 何校栋, 胡月. 用简单物理模型构建通用对称加密系统. , 2011, 60(9): 094701. doi: 10.7498/aps.60.094701
[9]	周庆, 陈钢, 胡月. 一个用简单物理模型构建的加密系统. , 2011, 60(4): 044701. doi: 10.7498/aps.60.044701
[10]	饶云江, 李立, 贾新鸿, 冉曾令, 张田虎. 基于拉曼组合放大的长距离光纤传输系统. , 2010, 59(7): 4682-4686. doi: 10.7498/aps.59.4682
[11]	徐丰, 陆明珠, 万明习, 方飞. 256阵元高强度聚焦超声相控阵系统误差与多焦点模式精确控制. , 2010, 59(2): 1349-1356. doi: 10.7498/aps.59.1349
[12]	钟文镇, 何克晶, 周照耀, 夏伟, 李元元. 粉末材料堆积的物理模型与仿真系统. , 2009, 58(13): 21-S28. doi: 10.7498/aps.58.21
[13]	李琦, 张波, 李肇基. 漂移区表面阶梯掺杂LDMOS的击穿电压模型. , 2008, 57(3): 1891-1896. doi: 10.7498/aps.57.1891
[14]	李琦, 张波, 李肇基. 双面阶梯埋氧层部分SOI高压器件新结构. , 2008, 57(10): 6565-6570. doi: 10.7498/aps.57.6565
[15]	吴亚波, 吕剑波, 李松, 杨秀一. 五维大反弹宇宙学模型的重建及其相关宇宙学量的演化. , 2008, 57(4): 2621-2626. doi: 10.7498/aps.57.2621
[16]	李潇, 刘亮, 张海英, 尹军舰, 李海鸥, 叶甜春, 龚敏. 一种新的磷化铟复合沟道高电子迁移率晶体管小信号物理模型. , 2006, 55(7): 3617-3621. doi: 10.7498/aps.55.3617
[17]	吴光, 周春源, 陈修亮, 韩晓红, 曾和平. 长距离长期稳定的量子密钥分发系统. , 2005, 54(8): 3622-3626. doi: 10.7498/aps.54.3622
[18]	杨祥林, 陈健. 增益噪声对光孤子通信系统码率距离积的限制. , 1993, 42(1): 51-57. doi: 10.7498/aps.42.51
[19]	张裕恒. 在一个磁通量子内dc Josephson电流阶梯或振荡效应的物理本质. , 1984, 33(2): 210-220. doi: 10.7498/aps.33.210
[20]	天体物理组. 试论现代宇宙学的发生和发展. , 1976, 25(4): 273-281. doi: 10.7498/aps.25.273

计量

文章访问数: 5512
PDF下载量: 243
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

哈勃常数危机