-
氘氚聚变产生的高能量α粒子是维持未来托卡马克反应堆等离子体高温的主要加热源, 良好的α粒子约束对于维持稳态燃烧等离子体至关重要. 在持续发生聚变反应的系统中, α粒子远离热平衡, 呈现非麦克斯韦分布. 如果忽略轨道效应, 基于局域库仑碰撞的假设可以得到α粒子的经典慢化分布, 然而由于α粒子存在较大的漂移轨道宽度, 空间输运不容忽视, 为得到更为准确的α粒子分布函数, 需要开展相关的数值计算. 本文使用模拟程序PTC (particle tracer code)在中国聚变工程试验堆(CFETR)不同的放电模式下, 采用粒子轨道跟踪和蒙特卡罗碰撞方法, 对α粒子慢化过程进行了数值模拟, 获得了更为真实的α粒子分布函数, 并将其与经典慢化分布进行了对比. 结果显示分布函数在中等能量附近和经典慢化分布存在较大差异. 进一步的分析表明, 这是由于中等能量下α粒子的较强的径向输运引起的. 本文的研究结果对准确评估α粒子加热背景等离子体的能力具有重要参考价值.The high-energy α particles produced by deuterium-tritium fusion are the primary heating source for maintaining high temperatures in future tokamak plasma. Effective confinement of α particles is crucial for sustaining steady-state burning plasma. The initial energy of α particles is
$ 3.5 {\text{ MeV}} $ . According to theoretical calculations, it takes approximately 1 second to slow down α particles through Coulomb collisions to an energy range similar to the energy range of the background plasma. In the slowing-down process, some α particles may be lost owing to various transport processes. One significant research problem is how to utilize α particles to effectively heat fuel ions so as to sustain fusion reactions in a reactor. Assuming local Coulomb collisions and neglecting orbital effects, a classical slowing-down distribution for α particles can be derived. However, considering the substantial drift orbit width of α particles and the importance of spatial transport, numerical calculations are required to obtain more accurate α particle distribution function. In this study, the particle tracer code (PTC) is used to numerically simulate the slowing-down process of α particles under different scenarios in the Chinese Fusion Engineering Test Reactor (CFETR). By combining particle orbit tracing method with Monte Carlo collision method, a more realistic α particle distribution function can be obtained and compared with the classical slowing-down distribution. The results show significant differences between this distribution function and the classical slowing-down distribution, particularly in the moderate energy range. Further analysis indicates that these disparities are primarily caused by the strong radial transport of α particles at these energy levels. The research findings hold profound implications for the precise evaluating of ability of α particles to heat the background plasma. Understanding and characterizing the behavior of α particles in the slowing-down process and their interaction with the plasma is critical for designing and optimizing future fusion reactors. By attaining a deeper comprehension of the spatial transport and distribution of α particles, it becomes possible to enhance the efficiency of fuel ion heating and sustain fusion reactions more effectively. This study establishes a foundation for subsequent investigations and evaluation of α particles as a highly efficient heating source for fusion plasmas.-
Keywords:
- tokamak /
- α particles /
- slowing-down distribution
[1] Jhang H, Chang C S 1996 Phys. Plasmas 3 3732
Google Scholar
[2] 赵海龙, 肖波, 王刚华, 王强, 章征伟, 孙奇志, 邓建军 2020 69 035203
Google Scholar
Zhao H L, Xiao B, Wang G H, Wang Q, Zhang Z W, Sun Q Z, Deng J J 2020 Acta Phys. Sin. 69 035203
Google Scholar
[3] Wan Y X, Li J G, Liu Y, Wang X L, Chan V, Chen C A, Duan X R, Fu P, Gao X, Feng K M 2017 Nucl. Fusion 57 102009
Google Scholar
[4] 李新霞, 李国壮, 刘洪波 2020 69 145201
Google Scholar
Li X X, Li G Z, Liu H B 2020 Acta Phys. Sin. 69 145201
Google Scholar
[5] Chen J L, Jian X, Chan V S, Li Z Y, Deng Z, Li G Q, Guo W F, Shi N, Chen X 2017 Plasma Phys. Controlled Fusion 59 75005
Google Scholar
[6] 郝保龙, 陈伟, 李国强, 王晓静, 王兆亮, 吴斌, 臧庆, 揭银先, 林晓东, 高翔, CFETR TEAM 2021 70 115201
Google Scholar
Hao B L, Chen W, Li G Q, Wang X J, Wang Z L, Wu B, Zang Q, Jie Y X, Lin X D, Gao X, CFETR T 2021 Acta Phys. Sin. 70 115201
Google Scholar
[7] McKee G R, Fonck R J, Stratton B C, Budny R V, Chang Z, Ramsey A T 1997 Nucl. Fusion 37 501
Google Scholar
[8] Kolesnichenko Y I 1980 Nucl. Fusion 20 727
Google Scholar
[9] Gorelenkov N N, Budny R V, Duong H H, Fisher R K, Medley S S, Petrov M P, Redi M H 1997 Nucl. Fusion 37 1053
Google Scholar
[10] 石黎铭, 吴雪科, 万迪, 李会东, 樊群超, 王中天, 冯灏, 王占辉, 马杰 2019 68 105201
Google Scholar
Shi L M, Wu X K, Wan D, Li H D, Fan Q C, Wang Z T, Feng H, Wang Z H, Ma J 2019 Acta Phys. Sin. 68 105201
Google Scholar
[11] He B, Wang Z G, Wang J G 2018 Phys. Plasmas 25 12704
Google Scholar
[12] Jhang H 2021 Phys. Plasmas 28 94501
Google Scholar
[13] Liberman M A, Velikovich A L 1984 J. Plasma Phys. 31 369
Google Scholar
[14] Hsu C T, Catto P J, Sigmar D J 1990 Phys. Fluids B 2 280
Google Scholar
[15] 陈忠, 赵子甲, 吕中良, 李俊汉, 潘冬梅 2019 68 215201
Google Scholar
Chen Z, Zhao Z J, Lü Z L, Li J H, Pan D M 2019 Acta Phys. Sin. 68 215201
Google Scholar
[16] Moseev D, Salewski M 2019 Phys. Plasmas 26 20901
Google Scholar
[17] Jhang H 1998 Phys. Plasmas 5 4498
Google Scholar
[18] Dai Y Z, Cao J J, Xiang D, Yang J H 2023 Phys. Plasmas 30 42501
Google Scholar
[19] Wilkie G J, Abel I G, Highcock E G, Dorland W 2015 J. Plasma Phys. 81 905810306
Google Scholar
[20] Angioni C, Peeters A G 2008 Phys. Plasmas 15 52307
Google Scholar
[21] Wilkie G J, Abel I G, Landreman M, Dorland W 2016 Phys. Plasmas 23 60703
Google Scholar
[22] Hauff T, Pueschel M J, Dannert T, Jenko F 2009 Phys. Rev. Lett. 102 75004
Google Scholar
[23] Sigmar D, Gormley R, Kamelander G 1993 Nucl. Fusion 33 677
Google Scholar
[24] Pueschel M J, Jenko F, Schneller M, Hauff T, Günter S, Tardini G 2012 Nucl. Fusion 52 103018
Google Scholar
[25] Wang F, Zhao R, Wang Z X, Zhang Y, Lin Z H, Liu S J 2021 Chin. Phys. Lett. 38 55201
Google Scholar
[26] Gaffey Jr J D 1976 J. Plasma Phys. 16 171
[27] Wilkie G J 2018 J. Plasma Phys. 84 745840601
Google Scholar
[28] Team J 1999 Nucl. Fusion 39 1619
Google Scholar
-
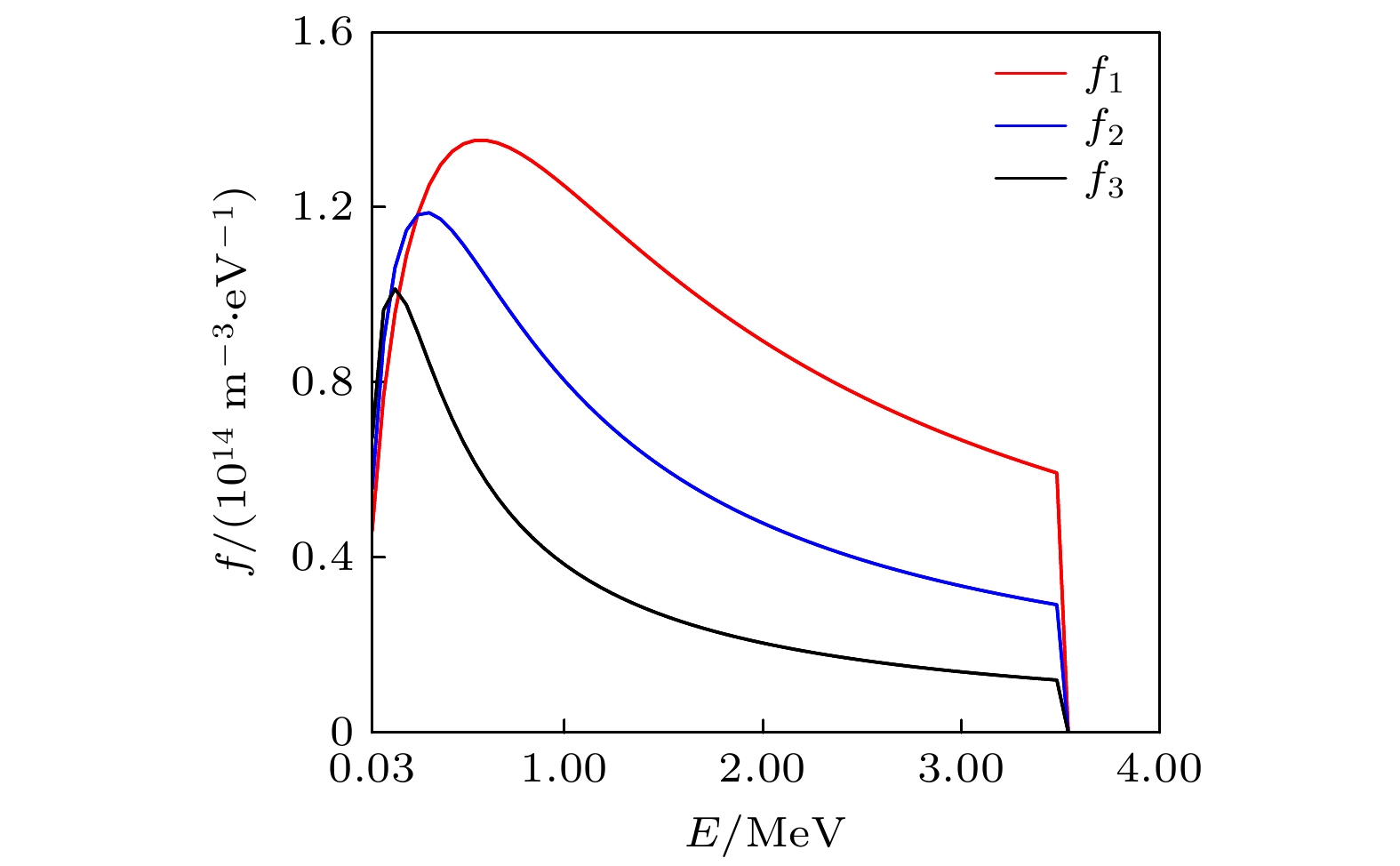
图 1 电子温度分别为27.78, 14.4和6.7 keV, 对应电子密度分别为1.14×1020, 9.34×1019和7.47×1019 m–3参数下得到的经典能量慢化分布
$ {f_1}, {\text{ }}{f_2}, {\text{ }}{f_3} $ Fig. 1. Classical energy slowing-down distributions f1, f2 and f3 obtained for the electron temperatures of 27.78, 14.4 and 6.7 keV, and their corresponding electron densities of 1.14×1020, 9.34×1019 and 7.47×1019 m–3.
图 2 CFETR中的背景等离子体参数 (a) 稳态运行模式下的密度、温度和安全因子剖面; (b) 混杂运行模式下的密度、温度和安全因子剖面
Fig. 2. Background plasma profiles in CFETR: (a) Density, temperature, and safety factor profiles in steady-state scenario; (b) density, temperature and safety factor profiles in hybrid scenario.
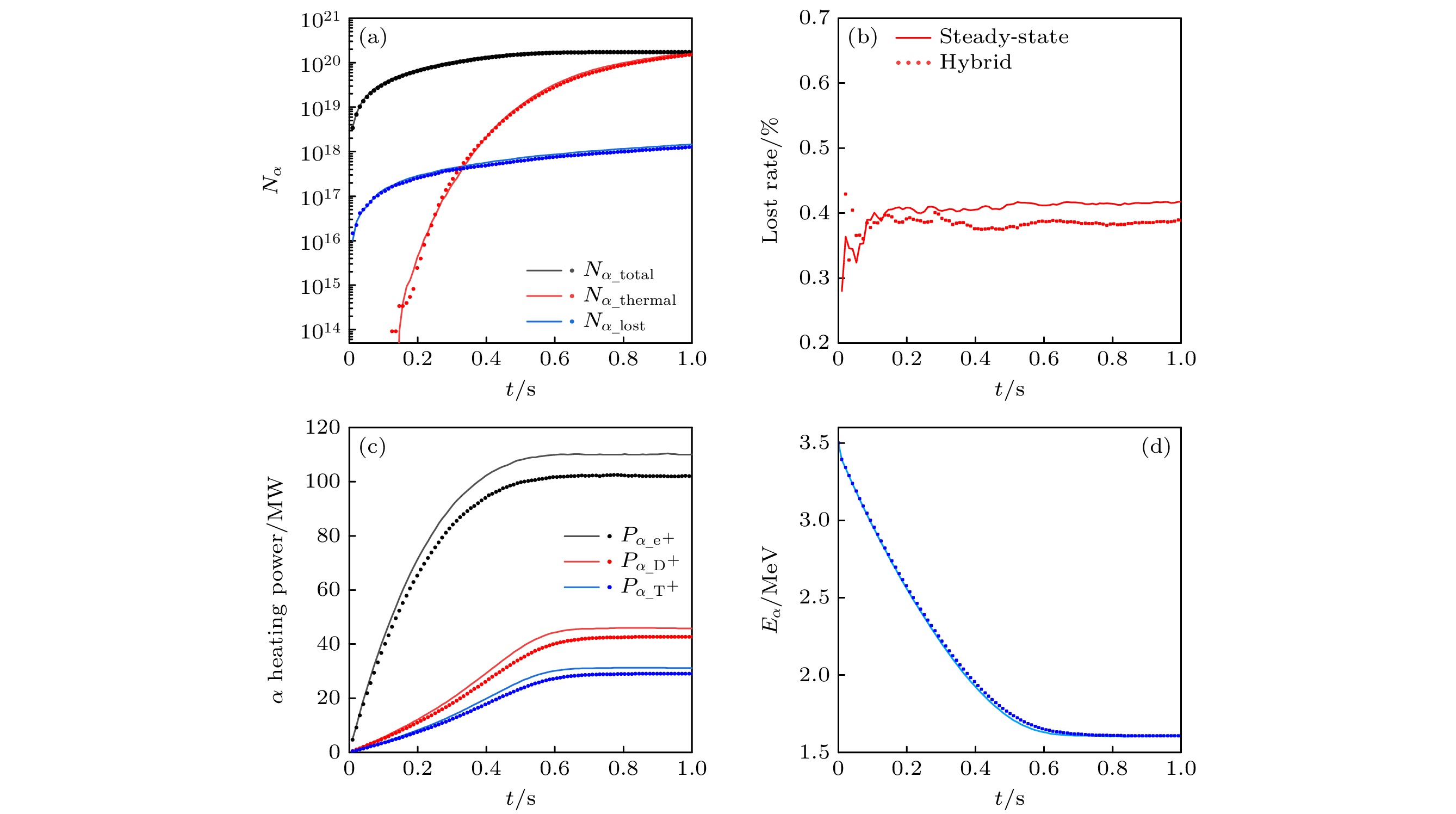
图 3 CFETR稳态运行模式(实线)和混杂运行模式(虚线)下的各个物理量随时间的变化 (a) α粒子数量; (b) α粒子损失率; (c) α粒子对背景等离子体的加热功率; (d) α粒子平均能量
Fig. 3. Time evolution of various physical quantities in CFETR steady-state scenario (solid lines) and hybrid scenario (dashed lines): (a) Number of α particles; (b) loss rate of α particles; (c) heating power of α particles to the background plasma; (d) average energy of α particles.
图 5 稳态时α粒子的密度分布 (a) CFETR稳态运行模式; (b) CFETR混杂运行模式
Fig. 5. The α particle density in steady-state: (a) CFETR steady-state scenario; (b) CFETR Hybrid scenario.
图 6 α粒子分布函数 (a) 能量空间; (b) 归一化极向磁通空间
Fig. 6. The α particle distribution function: (a) Energy space; (b) normalized poloidal magnetic flux space.
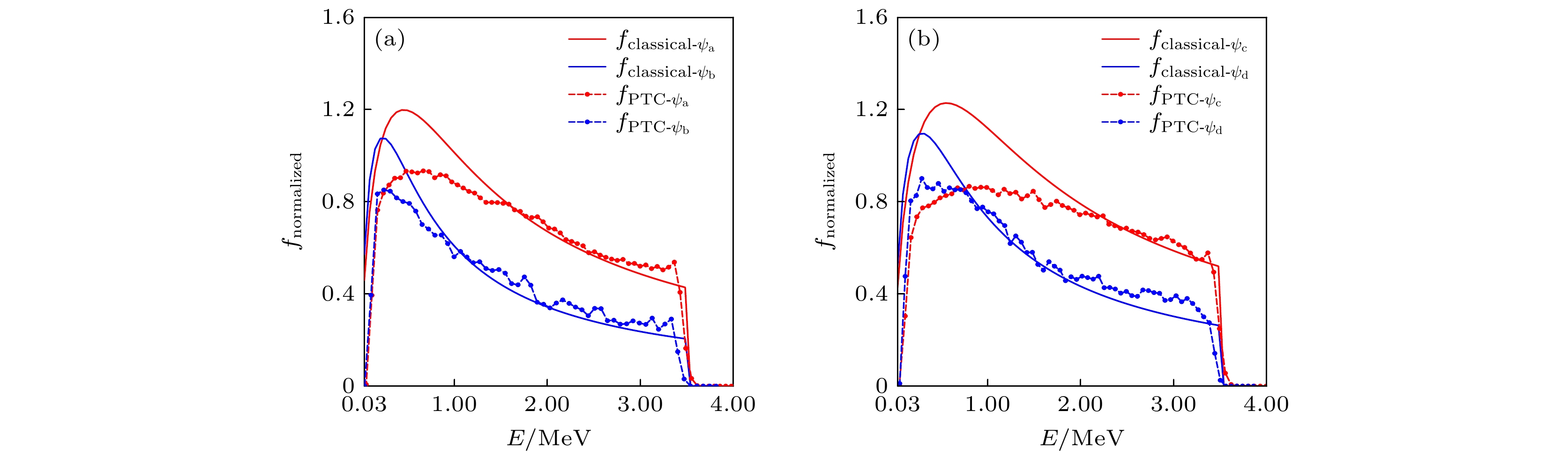
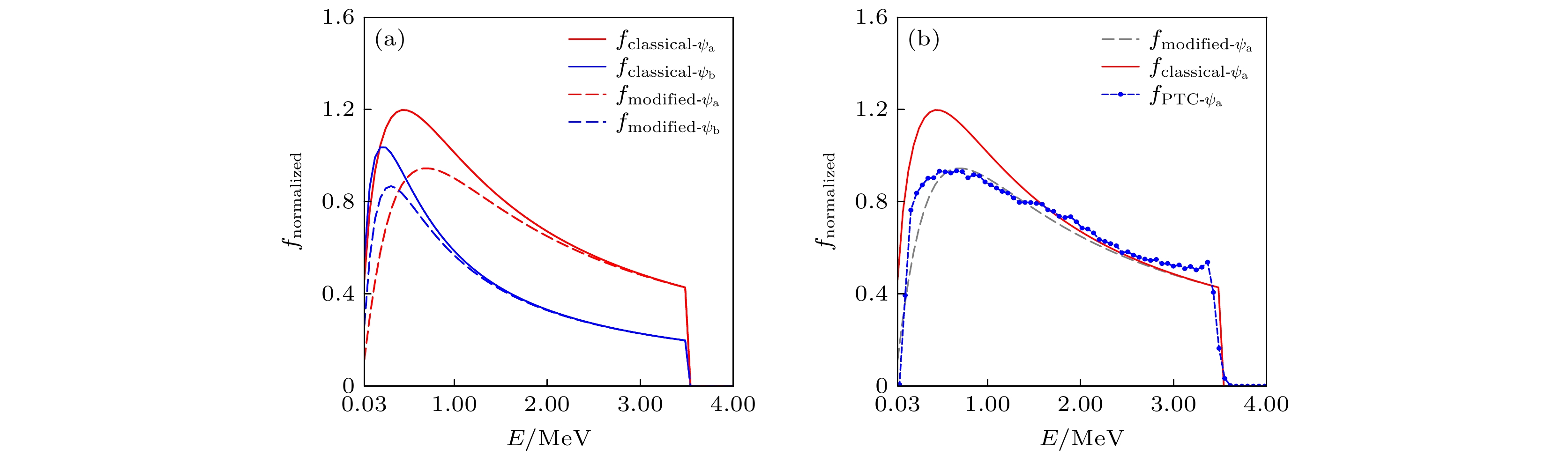
图 7 PTC程序得到的能量慢化分布与理论能量慢化分布的对比 (a) 稳态运行模式下
$ {\psi _{\text{a}}} = 0.1—0.2 $ 和$ {\psi _{\text{b}}} = 0.5\text{—}0.6 $ ; (b) 混杂运行模式下$ {\psi _{\text{c}}} = 0—0.1 $ 和$ {\psi _{\text{d}}} = 0.4—0.5 $ Fig. 7. Comparison between the energy slowing-down distribution obtained by PTC code and the classical energy slowing-down distribution: (a) In steady-state scenario at
$ {\psi _{\text{a}}} = 0.1$ –0.2 and$ {\psi _{\text{b}}} = 0.5$ –0.6 ; (b) in hybrid scenario at$ {\psi _{\text{c}}} = 0 $ –0.1 and$ {\psi _{\text{d}}} = $ $ 0.4$ –0.5.
图 8 稳态运行模式下的慢化分布函数对比 (a)
$ {\psi _{\text{a}}} = 0.1—0.2 $ 和$ {\psi _{\rm{b}}} = 0.5—0.6 $ 下经典慢化分布与修正慢化分布; (b)$ {\psi _{\text{a}}} = $ $ 0.1—0.2 $ 下修正慢化分布、经典慢化分布与PTC模拟的慢化分布Fig. 8. Comparison of slowing-down distribution functions in steady-state scenario: (a) Modified slowing-down distribution and classical slowing-down distribution at
$ {\psi _{\text{a}}} = 0.1-0.2 $ and$ {\psi _{\text{b}}} = 0.5-0.6 $ ; (b) modified slowing-down distribution, classical slowing-down distribution, and PTC slowing-down distribution at$ {\psi _{\text{a}}} = 0.1-0.2 $ . -
[1] Jhang H, Chang C S 1996 Phys. Plasmas 3 3732
Google Scholar
[2] 赵海龙, 肖波, 王刚华, 王强, 章征伟, 孙奇志, 邓建军 2020 69 035203
Google Scholar
Zhao H L, Xiao B, Wang G H, Wang Q, Zhang Z W, Sun Q Z, Deng J J 2020 Acta Phys. Sin. 69 035203
Google Scholar
[3] Wan Y X, Li J G, Liu Y, Wang X L, Chan V, Chen C A, Duan X R, Fu P, Gao X, Feng K M 2017 Nucl. Fusion 57 102009
Google Scholar
[4] 李新霞, 李国壮, 刘洪波 2020 69 145201
Google Scholar
Li X X, Li G Z, Liu H B 2020 Acta Phys. Sin. 69 145201
Google Scholar
[5] Chen J L, Jian X, Chan V S, Li Z Y, Deng Z, Li G Q, Guo W F, Shi N, Chen X 2017 Plasma Phys. Controlled Fusion 59 75005
Google Scholar
[6] 郝保龙, 陈伟, 李国强, 王晓静, 王兆亮, 吴斌, 臧庆, 揭银先, 林晓东, 高翔, CFETR TEAM 2021 70 115201
Google Scholar
Hao B L, Chen W, Li G Q, Wang X J, Wang Z L, Wu B, Zang Q, Jie Y X, Lin X D, Gao X, CFETR T 2021 Acta Phys. Sin. 70 115201
Google Scholar
[7] McKee G R, Fonck R J, Stratton B C, Budny R V, Chang Z, Ramsey A T 1997 Nucl. Fusion 37 501
Google Scholar
[8] Kolesnichenko Y I 1980 Nucl. Fusion 20 727
Google Scholar
[9] Gorelenkov N N, Budny R V, Duong H H, Fisher R K, Medley S S, Petrov M P, Redi M H 1997 Nucl. Fusion 37 1053
Google Scholar
[10] 石黎铭, 吴雪科, 万迪, 李会东, 樊群超, 王中天, 冯灏, 王占辉, 马杰 2019 68 105201
Google Scholar
Shi L M, Wu X K, Wan D, Li H D, Fan Q C, Wang Z T, Feng H, Wang Z H, Ma J 2019 Acta Phys. Sin. 68 105201
Google Scholar
[11] He B, Wang Z G, Wang J G 2018 Phys. Plasmas 25 12704
Google Scholar
[12] Jhang H 2021 Phys. Plasmas 28 94501
Google Scholar
[13] Liberman M A, Velikovich A L 1984 J. Plasma Phys. 31 369
Google Scholar
[14] Hsu C T, Catto P J, Sigmar D J 1990 Phys. Fluids B 2 280
Google Scholar
[15] 陈忠, 赵子甲, 吕中良, 李俊汉, 潘冬梅 2019 68 215201
Google Scholar
Chen Z, Zhao Z J, Lü Z L, Li J H, Pan D M 2019 Acta Phys. Sin. 68 215201
Google Scholar
[16] Moseev D, Salewski M 2019 Phys. Plasmas 26 20901
Google Scholar
[17] Jhang H 1998 Phys. Plasmas 5 4498
Google Scholar
[18] Dai Y Z, Cao J J, Xiang D, Yang J H 2023 Phys. Plasmas 30 42501
Google Scholar
[19] Wilkie G J, Abel I G, Highcock E G, Dorland W 2015 J. Plasma Phys. 81 905810306
Google Scholar
[20] Angioni C, Peeters A G 2008 Phys. Plasmas 15 52307
Google Scholar
[21] Wilkie G J, Abel I G, Landreman M, Dorland W 2016 Phys. Plasmas 23 60703
Google Scholar
[22] Hauff T, Pueschel M J, Dannert T, Jenko F 2009 Phys. Rev. Lett. 102 75004
Google Scholar
[23] Sigmar D, Gormley R, Kamelander G 1993 Nucl. Fusion 33 677
Google Scholar
[24] Pueschel M J, Jenko F, Schneller M, Hauff T, Günter S, Tardini G 2012 Nucl. Fusion 52 103018
Google Scholar
[25] Wang F, Zhao R, Wang Z X, Zhang Y, Lin Z H, Liu S J 2021 Chin. Phys. Lett. 38 55201
Google Scholar
[26] Gaffey Jr J D 1976 J. Plasma Phys. 16 171
[27] Wilkie G J 2018 J. Plasma Phys. 84 745840601
Google Scholar
[28] Team J 1999 Nucl. Fusion 39 1619
Google Scholar
下载:
计量
- 文章访问数: 2632
- PDF下载量: 108
- 被引次数: 0
