-
在二维材料中, 平面六方氮化铝(AlN)对开发电子器件至关重要. 但宽带隙限制了其应用, 为进一步突破性能瓶颈, 本文采用结构搜索的方法找到一种新型孔状皱面的AlN构型, 由于其特殊的孔状构型, 可在孔中引入C, Si原子与碳三角环(TC)形成新型二维X-AlN (X = C, Si, TC)结构, 从而提升其光学与热学性能. 结果表明: 1) 在电子结构方面, 由于X-pz电子的局域性, 费米面附近产生的孤立能带将带隙值从4.12 eV (AlN)分别降至0.65 (C-AlN)和1.85 eV (Si-AlN), 显著改善了AlN的宽带隙. TC-AlN由于碳三角环间C-pz杂化形成离域π键, 使能量降低, 实现了间接带隙到直接带隙的转变. 2) 热输运方面, 与AlN, C/Si-AlN相比, TC-AlN由于碳三角环间强共价键抑制了垂直面内的声子振动, 极大地增强了热导率. 此外, 在X-AlN中施加双轴应变, 热导率出现先上升后下降的异常变化趋势, 这是源于随应变增强的N—N键带来的低非谐性与声子模软化降低群速度之间的竞争. 本工作给出了调控二维AlN性能的新路径, 为提高半导体电子、光学与热学性能提供有力指导.Aluminum nitride (AlN) is of paramount importance in developing electronic devices because of excellent stability and thermal transport performance. However, lack of novel materials which can provide colorful physical and chemical properties seriously hinders further digging out application potential. In this work, we perform an evolutionary structural search based on first-principles calculation and verify the dynamic and thermal dynamic stability of porous buckled AlN and X-AlN (X = C, Si, TC) structural system, which constructs by introducing C, Si atoms and triangular carbon (TC) into the porous vacancy of AlN, by calculating phonon spectra and first-principles molecular dynamic simulations. Structural deformation becomes gradually serious with the increase of structural unit size and significantly influences structural, electronic, and thermal transport properties. Firstly, we point out that a flat energy band appears around the Fermi level in C-AlN and Si-AlN because of weak interatomic interaction between C/Si and the neighbor Al atoms. Unoccupied C-/Si-pz and Al-pz do not form
$ {\rm{\pi }} $ bond and only a localized flat band near Fermi level arises, and thus the absorption peaks of structures are enhanced and the red shift occurs. Bonding state of$ {\rm{\pi }} $ bond from hybridized C-pz orbitals in triangular carbon of TC-AlN lowers the energy of conduction band at K point in the first Brillouin zone and the corresponding antibonding state raises the band at Γ, therefore transition from indirect bandgap of AlN to direct bandgap of TC-AlN appears. Secondly, porous buckled AlN shows the lowest thermal conductivity due to asymmetric Al—N bonds around the porous vacancy and vertically stacked N—N bonds. Introduced C and Si atoms both reduce structural anharmonicity, while the former has a relatively small distortion, and so it has a higher thermal conductivity. Triangular carbon in TC-AlN hinders phonon scattering between FA mode and other phonon modes and has the weakest anharmonicity because of the strongest bond strength, and obtains the highest thermal transport performance. Finally, we unveil the physical mechanism of anomalous thermal conductivity in X-AlN system by modulating the biaxial tensile strain. Enhanced vertical N—N bonds dominate thermal transport due to its weaker anharmonicity with a slightly strain, and when tensile strain is above the 4%, soften phonon modes reduce phonon velocity and thus hinders the thermal transport process. Therefore, occurs the anomalous thermal transport behavior, i.e. thermal conductivity first rises and then drops with applied biaxial strain increasing. Our work paves the way for modulating two-dimensional AlN performance and provides a new insight for designing promising novel two-dimensional semiconductors.-
Keywords:
- two-dimensional semiconductor /
- thermal transport /
- electronic structure /
- biaxial stress-strain
[1] Robinson J A 2018 APL Mater. 6 058202
Google Scholar
[2] Shi L, Xu A, Zhao T 2017 ACS Appl. Mater. Interfaces 9 1987
Google Scholar
[3] Cai Y, Liu Y, Xie Y, Zou Y, Gao C, Zhao Y, Liu S, Xu H, Shi J, Guo S, Sun C 2020 APL Mater. 8 021107
Google Scholar
[4] 叶倩, 沈阳, 袁野, 赵祎峰, 段纯刚 2020 69 217710
Google Scholar
Ye Q, Shen Y, Yuan Y, Zhao Y F, Duan C G 2020 Acta Phys. Sin. 69 217710
Google Scholar
[5] 陈蓉, 王远帆, 王熠欣, 梁前, 谢泉 2022 71 127301
Google Scholar
Chen R, Wang Y F, Wang Y X, Liang Q, Xie Q 2022 Acta Phys. Sin. 71 127301
Google Scholar
[6] Liang H P, Duan Y F 2022 Chin. Phys. B 31 076301
Google Scholar
[7] Lü F, Liang H P, Duan Y F 2023 J. Phys. Chem. Lett. 14 663
Google Scholar
[8] Wan X G, Turner A M, Vishwanath A, Savrasov S Y 2011 Phys. Rev. B 83 205101
Google Scholar
[9] Liang H P, Duan Y F 2021 Nanoscale 13 11994
Google Scholar
[10] Akal L, Kusuki Y, N Shiba, Takayanagi T, Wei Z X 2021 Phys. Rev. Lett. 126 061604
Google Scholar
[11] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A 2004 Science 306 666
Google Scholar
[12] 卢晓波, 张广宇 2015 64 077305
Google Scholar
Lu X B, Zhang G Y 2015 Acta Phys. Sin. 64 077305
Google Scholar
[13] Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43
Google Scholar
[14] Tan X, Xin Z Y, Liu X J, Mu Q G 2013 Adv. Mater. Research 821 841
[15] Shimada K, Sota T, Suzuki K 1998 J. Appl. Phys. 84 4951
Google Scholar
[16] Zhang H, Yu S, Liu F, Wang Z, Lu M, Hu X, Chen Y, Xu X 2017 Sci. Chin. Phys. Mech. Astron. 60 044311
Google Scholar
[17] 冯嘉恒, 唐立丹, 刘邦武, 夏洋, 王冰 2013 62 116302
Google Scholar
Feng J H, Tang L D, Liu B W, Xia Y, Wang B 2013 Acta Phys. Sin. 62 116302
Google Scholar
[18] 林竹, 郭志友, 毕艳君, 董玉成 2009 58 191707
Google Scholar
Lin Z, Guo Z Y, Bi Y Z, Dong Y C 2009 Acta phys. Sin. 58 191707
Google Scholar
[19] 程丽, 王德兴, 张杨, 苏丽萍, 陈淑妍, 王晓峰, 孙鹏, 易重桂 2018 67 047101
Google Scholar
Cheng L, Wang D X, Zhang Y, Su L P, Chen S Y, Wang X F, Sun P, Yi C G 2018 Acta Phys. Sin. 67 047101
Google Scholar
[20] 高小奇, 郭志友, 曹东兴, 张宇飞, 孙慧卿, 邓贝 2010 59 3418
Google Scholar
Gao X Q, Guo Z Y, Cao D X, Zhang Y F, Sun H Q, Deng B 2010 Acta Phys. Sin. 59 3418
Google Scholar
[21] de Almeida Jr E F, de Brito Mota F, de Castilho C M C, Kakanakova-Georgieva A, Gueorguiev G K 2012 Eur. Phys. J. B 85 48
Google Scholar
[22] Jia Y P, Shi Z M, Hou W T, Zang H, Jiang K, Chen Y, Zhang S L, Qi Z B, Wu T, Sun X J, Li D B 2020 Npj 2D Mater. Appl. 4 31
Google Scholar
[23] Gürbüz E, Cahangirov S, Durgun E, Ciraci S 2017 Phys. Rev. B 96 205427
Google Scholar
[24] Zhou R, Liang H P, Duan Y F, Wei S H 2023 J. Phys. Chem. Lett. 14 737
Google Scholar
[25] Sheng X L, Yan Q B, Ye F, Zheng Q R, Su G 2011 Phys. Rev. Lett. 106 155703
Google Scholar
[26] Zhang J, Wang R, Zhu X, Pan A, Han C, Li X, Zhao D, Ma C, Wang Q, Su H, Niu C 2017 Nat. Commun. 8 683
Google Scholar
[27] Liu W H, Luo J W, Li S, Wang L W 2020 Phys. Rev. B 102 184308
Google Scholar
[28] Liang H P, Zhong H Z, Huang S, Duan Y F 2021 J. Phys. Chem. Lett. 12 10975
Google Scholar
[29] Oganov A R, Ma Y, Lyahov A O, Valle M, Gatti C 2010 Rev. Mineral. Geochem. 71 271
Google Scholar
[30] Oganov A R, Lyahov A O, Valle M 2011 Acc. Chem. Res. 44 227
Google Scholar
[31] Oganov A R, Class C W 2006 J. Chem. Phys. 124 244704
Google Scholar
[32] Hohenberg P, Kohn W 1964 Phys. Rev. 136 B864
Google Scholar
[33] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133
Google Scholar
[34] Kresse H, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[35] Kresse H, Hafner J 1994 Phys. Rev. B 49 14251
Google Scholar
[36] Kresse H, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[37] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[38] Heyd J, Scueria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207
Google Scholar
[39] Jia W, Fu J, Cao Z, Wang L, Chi X, Gao W, Wang L W 2013 Comput. Phys. Commun. 251 102
Google Scholar
[40] Jia W, Cao Z, Wang L, Fu J, Chi X, Gao W, Wang L W 2013 Comput. Phys. Commun. 184 9
Google Scholar
[41] Atsush T, Isa T 2015 Scr. Mater. 108 1
Google Scholar
[42] Li W, Carrete J, Katcho N A, Mingo N 2014 Comput. Phys. Commun. 185 1747
Google Scholar
[43] Homayoun J, Bahram A R, Mahdi F 2018 Solid State Commun. 282 21
Google Scholar
[44] 程正富, 郑瑞伦 2016 65 104701
Google Scholar
Cheng Z F, Zheng R L 2016 Acta Phys. Sin. 65 104701
Google Scholar
[45] Lü F, Liang H P, Duan Y F 2023 Phys. Rev. B 107 045422
Google Scholar
[46] Koh Y R, Mamun A, Bin Hoque M S, Liu Z Y, Bai T Y, Hussain K, Liao M E, Li R Y, Gaskins J T, Giri A, Tomko J, Braun J L, Gaevski M, Lee E, Yates L, Goorsky M S, Luo T F, Khan A, Graham S, Hopkins P E 2020 ACS Appl. Mater. Interfaces 12 29443
[47] Mortazavi B, Shahrokhi M, Raeisi M, Zhuang X, Pereira L F C, Rabczuk T 2019 Carbon 149 733
Google Scholar
[48] Lindsay L, Broido D A, Mingo N 2010 Phys. Rev. B 82 115427
Google Scholar
-
图 1 孔状皱面AlN以及由AlN的孔中引入C, Si原子与碳三角环的C-AlN, Si-AlN和TC-AlN的晶格结构
Fig. 1. Lattice structure of porous buckled AlN and AlN-C, AlN-Si and AlN-TC, which construct by introducing C, Si atoms and triangular carbon (TC) in AlN.
图 2 (a) AlN, (b) C-AlN, (c) Si-AlN 与 (d) TC-AlN的电子结构及其态密度. 费米面附近能带的部分电荷分布图插入在电子结构图中
Fig. 2. Electronic structure and density of states of (a) AlN, (b) C-AlN, (c) Si-AlN, and (d) TC-AlN. Partial charge distributions of the band near the Fermi level are inserted in the electronic structures.
图 3 孔状皱面AlN与X-AlN (X = C, Si, TC)的光吸收系数
Fig. 3. Optical absorption coefficients of porous buckled AlN and X-AlN (X = C, Si, TC).
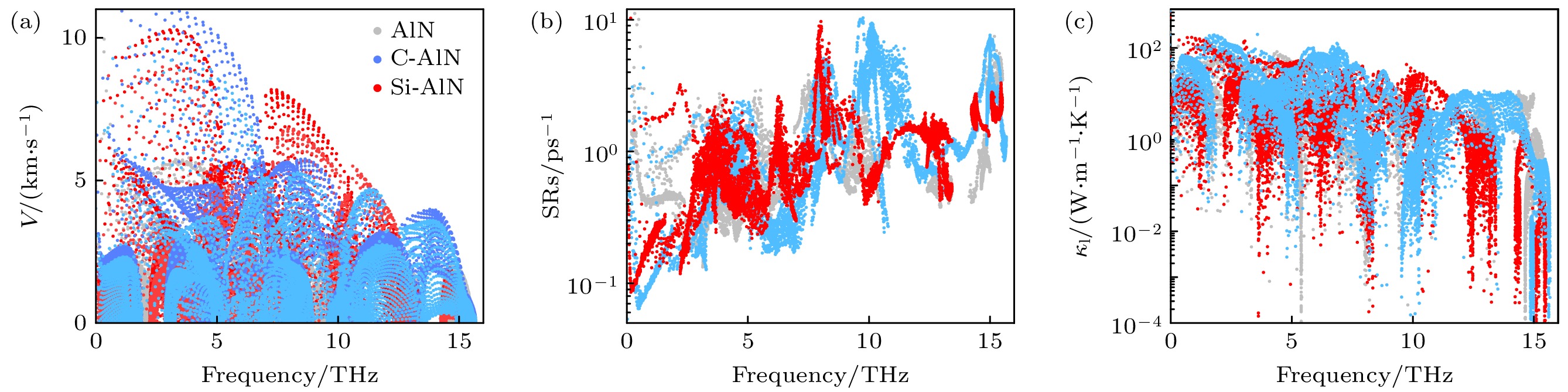
图 4 孔状皱面AlN与X-AlN (X = C, Si, TC)的(a)在300 K下的晶格热导率, (b) 各声子支相对热导贡献, (d) 声子弛豫时间与(e) 声子群速度平方. (c) TC-AlN前九支声子支非谐散射率在第一布里渊区中的分布. 图(a)中的插图为随温度变化的晶格热导率; 图(b)中的插图为TC-AlN声子支的热导贡献
Fig. 4. (a) Lattice thermal conductivity at 300 K, (b) relative thermal conductivity contribution of each phonon branch, (d) phonon relaxation time and (e) square of phonon group velocity for porous buckled AlN and X-AlN (X = C, Si, TC). (c) The distribution of anharmonic scattering rates of the first 9 phonon branches of TC-AlN in the first Brillouin zone. The lattice thermal conductivity versus temperature is inserted in panel (a); the thermal conductivity contribution of each phonon branch of TC-AlN is inserted in panel (b).
图 5 孔状皱面AlN与X-AlN (X = C, Si)随频率变化的(a)声子群速度、(b)非谐散射率和(c)晶格热导率
Fig. 5. (a) Phonon group velocity, (b) anharmonic scattering rates, and (c) lattice thermal conductivity versus frequency for porous buckled AlN and X-AlN (X = C, Si).
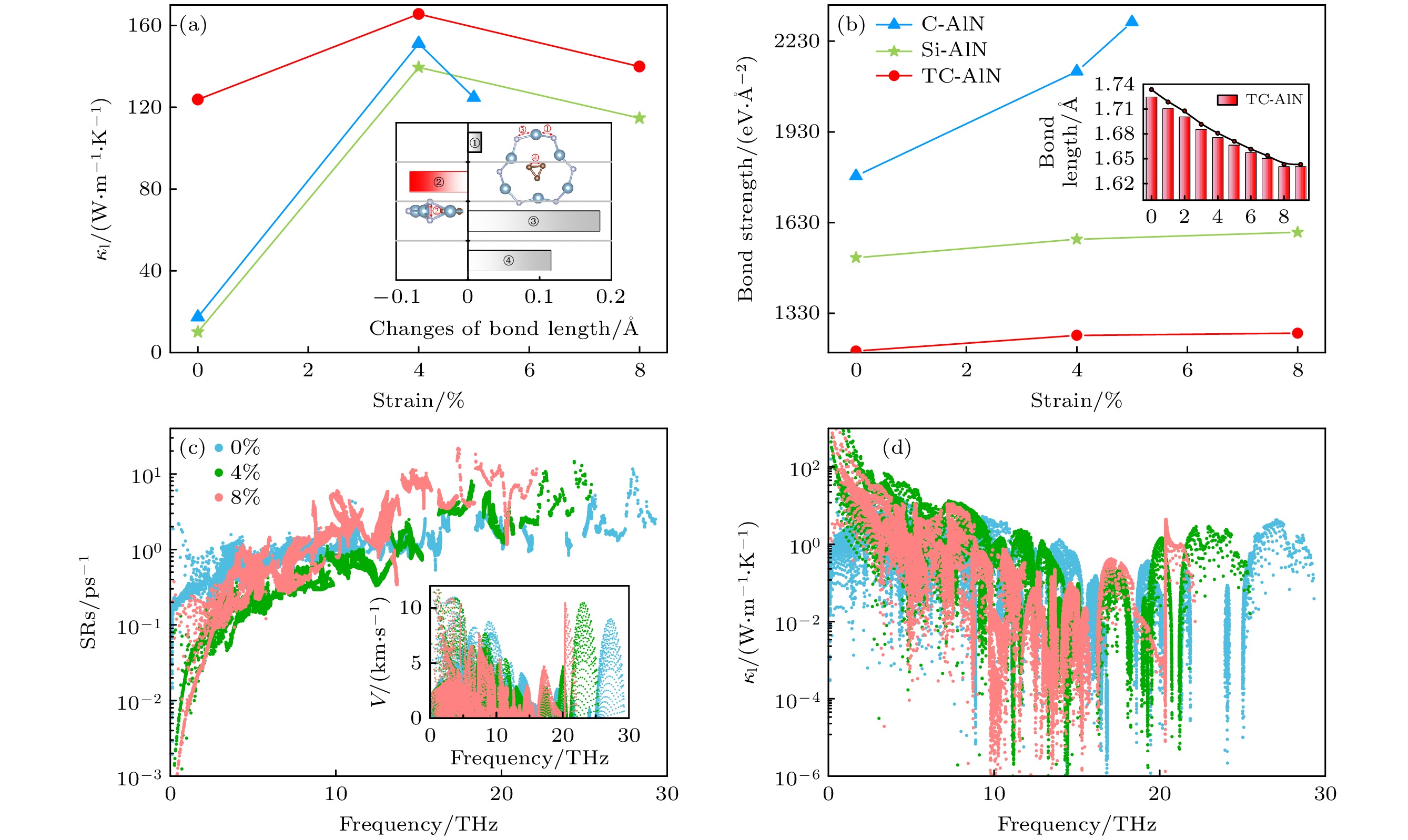
图 6 在不同应变下X-AlN (X = C, Si, TC)的(a) 300 K下晶格热导率、(b) N—N键键强. TC-AlN的(c)非谐散射率与(d)频率变化的晶格热导. 8%应力下N—N键键长改变量、随应力变化的键长与群速度作为插图分别在图(a), 图(b), 图(c) 中
Fig. 6. (a) Lattice thermal conductivity at 300 K and (b) N—N bond strength at different strains for X-AlN (X = C, Si and TC). (c) Anharmonic scattering rates and (d) lattice thermal conductivity distribution versus frequency for TC-AlN. The changes of N—N bond length at 8% strain, bond lengths with variation of strains, and group velocity of TC-AlN as the insets of panels (a), (b), and (c), respectively.
表 1 X-AlN (X = C, Si, TC)的结构参数与电子、结构和热学性质. 其中键角
$ \alpha $ 为孔状空位边缘N—Al—N的角度, 键长为所引入原子X与临近Al成键的键长Table 1. Structural parameters and electronic, structural and thermal properties of X-AlN (X = C, Si, TC). Bond angle
$ \alpha $ locates at the N—Al—N near the porous vacancy, and bond length is the distance between the introduced atoms and the neighbor Al.结构 晶格常数/Å 键角$ \alpha / $(°) 键长/Å 杨氏模量 /(N·m–1) 泊松比 带隙/eV 热导率/(W·m–1·K–1) AlN 5.12 113.90 — 70.57 0.39 4.12/间接 6.86 C-AlN 5.51 122.08 1.94 89.02 0.50 0.65/间接 17.30 Si-AlN 5.89 138.38 2.44 79.28 0.47 1.85/间接 10.08 TC-AlN 6.08 167.63 1.96 90.95 0.41 3.95/直接 123.75 
下载: 导出CSV
-
[1] Robinson J A 2018 APL Mater. 6 058202
Google Scholar
[2] Shi L, Xu A, Zhao T 2017 ACS Appl. Mater. Interfaces 9 1987
Google Scholar
[3] Cai Y, Liu Y, Xie Y, Zou Y, Gao C, Zhao Y, Liu S, Xu H, Shi J, Guo S, Sun C 2020 APL Mater. 8 021107
Google Scholar
[4] 叶倩, 沈阳, 袁野, 赵祎峰, 段纯刚 2020 69 217710
Google Scholar
Ye Q, Shen Y, Yuan Y, Zhao Y F, Duan C G 2020 Acta Phys. Sin. 69 217710
Google Scholar
[5] 陈蓉, 王远帆, 王熠欣, 梁前, 谢泉 2022 71 127301
Google Scholar
Chen R, Wang Y F, Wang Y X, Liang Q, Xie Q 2022 Acta Phys. Sin. 71 127301
Google Scholar
[6] Liang H P, Duan Y F 2022 Chin. Phys. B 31 076301
Google Scholar
[7] Lü F, Liang H P, Duan Y F 2023 J. Phys. Chem. Lett. 14 663
Google Scholar
[8] Wan X G, Turner A M, Vishwanath A, Savrasov S Y 2011 Phys. Rev. B 83 205101
Google Scholar
[9] Liang H P, Duan Y F 2021 Nanoscale 13 11994
Google Scholar
[10] Akal L, Kusuki Y, N Shiba, Takayanagi T, Wei Z X 2021 Phys. Rev. Lett. 126 061604
Google Scholar
[11] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A 2004 Science 306 666
Google Scholar
[12] 卢晓波, 张广宇 2015 64 077305
Google Scholar
Lu X B, Zhang G Y 2015 Acta Phys. Sin. 64 077305
Google Scholar
[13] Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43
Google Scholar
[14] Tan X, Xin Z Y, Liu X J, Mu Q G 2013 Adv. Mater. Research 821 841
[15] Shimada K, Sota T, Suzuki K 1998 J. Appl. Phys. 84 4951
Google Scholar
[16] Zhang H, Yu S, Liu F, Wang Z, Lu M, Hu X, Chen Y, Xu X 2017 Sci. Chin. Phys. Mech. Astron. 60 044311
Google Scholar
[17] 冯嘉恒, 唐立丹, 刘邦武, 夏洋, 王冰 2013 62 116302
Google Scholar
Feng J H, Tang L D, Liu B W, Xia Y, Wang B 2013 Acta Phys. Sin. 62 116302
Google Scholar
[18] 林竹, 郭志友, 毕艳君, 董玉成 2009 58 191707
Google Scholar
Lin Z, Guo Z Y, Bi Y Z, Dong Y C 2009 Acta phys. Sin. 58 191707
Google Scholar
[19] 程丽, 王德兴, 张杨, 苏丽萍, 陈淑妍, 王晓峰, 孙鹏, 易重桂 2018 67 047101
Google Scholar
Cheng L, Wang D X, Zhang Y, Su L P, Chen S Y, Wang X F, Sun P, Yi C G 2018 Acta Phys. Sin. 67 047101
Google Scholar
[20] 高小奇, 郭志友, 曹东兴, 张宇飞, 孙慧卿, 邓贝 2010 59 3418
Google Scholar
Gao X Q, Guo Z Y, Cao D X, Zhang Y F, Sun H Q, Deng B 2010 Acta Phys. Sin. 59 3418
Google Scholar
[21] de Almeida Jr E F, de Brito Mota F, de Castilho C M C, Kakanakova-Georgieva A, Gueorguiev G K 2012 Eur. Phys. J. B 85 48
Google Scholar
[22] Jia Y P, Shi Z M, Hou W T, Zang H, Jiang K, Chen Y, Zhang S L, Qi Z B, Wu T, Sun X J, Li D B 2020 Npj 2D Mater. Appl. 4 31
Google Scholar
[23] Gürbüz E, Cahangirov S, Durgun E, Ciraci S 2017 Phys. Rev. B 96 205427
Google Scholar
[24] Zhou R, Liang H P, Duan Y F, Wei S H 2023 J. Phys. Chem. Lett. 14 737
Google Scholar
[25] Sheng X L, Yan Q B, Ye F, Zheng Q R, Su G 2011 Phys. Rev. Lett. 106 155703
Google Scholar
[26] Zhang J, Wang R, Zhu X, Pan A, Han C, Li X, Zhao D, Ma C, Wang Q, Su H, Niu C 2017 Nat. Commun. 8 683
Google Scholar
[27] Liu W H, Luo J W, Li S, Wang L W 2020 Phys. Rev. B 102 184308
Google Scholar
[28] Liang H P, Zhong H Z, Huang S, Duan Y F 2021 J. Phys. Chem. Lett. 12 10975
Google Scholar
[29] Oganov A R, Ma Y, Lyahov A O, Valle M, Gatti C 2010 Rev. Mineral. Geochem. 71 271
Google Scholar
[30] Oganov A R, Lyahov A O, Valle M 2011 Acc. Chem. Res. 44 227
Google Scholar
[31] Oganov A R, Class C W 2006 J. Chem. Phys. 124 244704
Google Scholar
[32] Hohenberg P, Kohn W 1964 Phys. Rev. 136 B864
Google Scholar
[33] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133
Google Scholar
[34] Kresse H, Hafner J 1993 Phys. Rev. B 47 558
Google Scholar
[35] Kresse H, Hafner J 1994 Phys. Rev. B 49 14251
Google Scholar
[36] Kresse H, Furthmüller J 1996 Phys. Rev. B 54 11169
Google Scholar
[37] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[38] Heyd J, Scueria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207
Google Scholar
[39] Jia W, Fu J, Cao Z, Wang L, Chi X, Gao W, Wang L W 2013 Comput. Phys. Commun. 251 102
Google Scholar
[40] Jia W, Cao Z, Wang L, Fu J, Chi X, Gao W, Wang L W 2013 Comput. Phys. Commun. 184 9
Google Scholar
[41] Atsush T, Isa T 2015 Scr. Mater. 108 1
Google Scholar
[42] Li W, Carrete J, Katcho N A, Mingo N 2014 Comput. Phys. Commun. 185 1747
Google Scholar
[43] Homayoun J, Bahram A R, Mahdi F 2018 Solid State Commun. 282 21
Google Scholar
[44] 程正富, 郑瑞伦 2016 65 104701
Google Scholar
Cheng Z F, Zheng R L 2016 Acta Phys. Sin. 65 104701
Google Scholar
[45] Lü F, Liang H P, Duan Y F 2023 Phys. Rev. B 107 045422
Google Scholar
[46] Koh Y R, Mamun A, Bin Hoque M S, Liu Z Y, Bai T Y, Hussain K, Liao M E, Li R Y, Gaskins J T, Giri A, Tomko J, Braun J L, Gaevski M, Lee E, Yates L, Goorsky M S, Luo T F, Khan A, Graham S, Hopkins P E 2020 ACS Appl. Mater. Interfaces 12 29443
[47] Mortazavi B, Shahrokhi M, Raeisi M, Zhuang X, Pereira L F C, Rabczuk T 2019 Carbon 149 733
Google Scholar
[48] Lindsay L, Broido D A, Mingo N 2010 Phys. Rev. B 82 115427
Google Scholar
下载:
计量
- 文章访问数: 3954
- PDF下载量: 94
- 被引次数: 0
