-
含自由液面的汇流旋涡抽吸演变中存在多相耦合、物质传输、能量剧烈交换等物理过程, 其中所涉及的多相流体耦合输运机理是具有高度非线性特征的复杂动力学问题, 多相黏滞耦合输运动力学建模与数值求解具有较高难度. 针对上述问题, 提出一种含自由液面的汇流旋涡多相耦合输运建模与求解方法. 基于水平集-流体体积耦合(CLSVOF)计算方法, 结合连续表面张力模型和可实现(k-ε)湍流模型, 建立含自由液面的汇流旋涡多相耦合输运动力学模型; 利用一种有效的体积修正方案来计算高速旋转多相流, 保证流场质量守恒和无散度的速度场; 结合相间耦合求解策略对多相流体分布与多相界面进行精确追踪. 基于旋流场多特征物理变量, 得到多相耦合界面动态演变与跨尺度涡团输运规律, 揭示了多相耦合输运过程与压力脉动特性之间的相互作用机理. 研究结果表明: 多相耦合输运过程是流体介质过渡的关键状态, 旋涡微团受到不同时空扰动模式在界面处形成层层螺纹波形; 旋涡多相耦合输运过程随着水口尺度增大而增强, 且耦合能量激波引起非线性压力脉动现象. 研究结果可为旋涡输运机理、涡团跨尺度求解、流型追踪等方面的研究提供有益借鉴.
-
关键词:
- 自由汇流旋涡 /
- 多相耦合输运 /
- 水平集-流体体积耦合方法 /
- 体积修正 /
- 压力脉动
In the evolution of confluence sink vortex with a free surface, there exists some physical processes , such as multiphase coupling, mass transfer, and intensive energy exchange. Here, the transport mechanism of multiphase coupling is a complex dynamic problem with highly nonlinear characteristics. The mechanical modeling and numerical solution of multiphase viscous coupled transport are facing a significant challenge. To address the above problem, a method of modeling and solving multiphase coupling transport of the free sink vortex is proposed. Based on the coupled level set and volume-of-fluid (CLSVOF) method, a multiphase coupling transport model of the free sink vortex is set up with a continuous surface tension model and a realizable (k-ε) turbulence model. By using an effective volumetric correction scheme, the high-speed rotating flow is calculated, and the mass conservation of flow field and the velocity field without divergence are ensured. Then, an interphase coupling solution approach accurately traces the multiphase fluid distribution and multiphase interface. The multiphase coupling interface and cross-scale vortex cluster transport laws are obtained according to the multi-characteristic physical variables. The interaction mechanism between the multiphase coupling transport process and the pressure pulsation characteristics is revealed. The results show that the multiphase coupling transport is the critical state of the fluid medium transition. The vortex microclusters are subjected to different spatiotemporal disturbance modes and form the layered threaded waveforms at the interface. With the increase of the nozzle sizes, the multiphase coupling process is strengthened, and the coupling energy shock causes nonlinear pressure pulsation. This study can offer valuable references to the researches of the vortex transport mechanism, cross-scale solution of vortex cluster, and flow pattern tracking.-
Keywords:
- free sink vortex /
- multiphase coupling transport /
- coupled level set and volume-of-fluid method /
- volume correction /
- pressure pulsation
[1] Li L, Tan D P, Yin Z C, Wang T, Fan X H, Wang R H 2021 Renew. Energ. 175 887
Google Scholar
[2] Tan D P, Li L, Yin Z C, Li D F, Zhu Y L, Zheng S 2021 Int. J. Heat Mass Transfer. 150 119250
Google Scholar
[3] 谭大鹏, 杨涛, 赵军 2016 65 054701
Google Scholar
Tan D P, Tao Y, Zhao J 2016 Acta Phys. Sin. 65 054701
Google Scholar
[4] Li L, Tan D P, Wang T, Yin Z C, Fan X H, Wang R H 2021 Energy 216 119136
Google Scholar
[5] Aboelkassem Y, Georgicis V 2007 J. Fluids Eng. Trans. ASME 129 1073
Google Scholar
[6] Chen Y C, Huang S L, Li Z Y, Chang C C, Chu C C 2013 J. Fluid Mech. 733 134
Google Scholar
[7] Tan Y F, Ni Y S, Wu J F, Li L, Tan D P 2023 Int. J. Adv. Manuf. Technol. DOI: 10.1007/s00170-022-10761-8 (in Press)
[8] Tahershamsi A, Rahimzadeh H, Monshizadeh M, Sarkardeh H 2018 Meccanica 53 3269
Google Scholar
[9] Tan D P, Ni Y S, Zhang L B 2017 J. Iron Steel Res. Int. 24 669
Google Scholar
[10] Morales R D, Dávila–Maldonado O, Calderón I 2013 ISIJ Int. 53 782
Google Scholar
[11] Yang M, Liu S, Xu W H 2020 ACS Omega 5 31332
Google Scholar
[12] Škerlavaj A, Škerget L, Ravnik J 2014 Eng. Appl. Comp. Fluid Mech. 8 193
Google Scholar
[13] Ahn S H, Xiao Y X, Wang Z W, Zhou X Z, Luo Y Y 2017 Renew. Energ. 101 617
Google Scholar
[14] Li L, Qi H, Yin Z C, Li D F, Zhu Z L, Tangwarodomnukun V, Tan D P 2020 Powder Technol. 360 462
Google Scholar
[15] Zheng G A, Gu Z H, Xu W X, Li Q H, Tan Y F, Wang C Y, Li L 2023 Proesses 11 42
Google Scholar
[16] Ling K, Zhang S, Wu P Z, Yang S Y, Tao W Q 2019 Int. J. Heat Mass Transf. 143 118565
Google Scholar
[17] Tan D P, Li L, Zhu Y L, Zheng S, Yin Z C, Li D F 2019 J. Zhejiang Univ.-SCI A 20 61
Google Scholar
[18] 谭大鹏, 计时鸣, 李培玉 2010 中国科学-技术科学 53 2378
Google Scholar
Tan D P, Ji S M, Li P Y 2010 Sci. China-Technol. Sci. 53 2378
Google Scholar
[19] Duan G T, Chen B, Zhang X M, Wang Y C 2017 Comput. Method Appl. Eng. 320 133
Google Scholar
[20] Qian J Y, Zhao L, Li X J, Li Q Q, Jin Z J 2022 J. Zhejiang Univ.-SCI A. 23 783
Google Scholar
[21] Tan D P, Li L, Zhu Y L, Zheng S, Ruan H J, Jiang X Y 2018 IEEE Trans. Ind. Inform. 14 2881
Google Scholar
[22] Wang J X, Gao S B, Tang Z J, Tan D P 2021 J. Intell.Manuf. DOI: 10.1007/s10845-021-01854-4 (in Press)
[23] Tan D P, Zhang L B 2014 Sens. Actuator. B 202 1257
Google Scholar
[24] Pan Y, Ji S M, Tan D P, Cao H Q 2020 Int. J. Manuf. Technol. 109 2587
Google Scholar
[25] Li L, Yang Y S, Xu W X, Lu B, Gu Z H, Yang J G, Tan D P 2021 Appl. Sci. 12 8538
Google Scholar
[26] Yin Z C, Ni Y S, Li L, Wang T, Wu J F, Li Z, Tan D P 2022 J. Zhejiang Univ.-SCI A DOI: 10.1631/jzus.A2200014 (in Press)
[27] Li L, Xu W X, Tan Y F, Yang Y S, Yang J G, Tan D P 2023 Mech. Syst. Signal Process 189 110058
Google Scholar
[28] Gen J Q, Ji S M, Tan D P 2018 J. Adv. Manuf. Technol. 95 1069
Google Scholar
[29] Ruan Y M, Yao Y, Shen S Y, Wang B, Wang B, Zhang J Y, Huang J K 2020 Steel Res. Int. 91 1900616
Google Scholar
[30] Zheng S H Yu Y K, Qiu M Z, Wang L M, Tan D P 2021 Appl. Math. Model. 91 934
Google Scholar
[31] Ge M, Ji S M, Tan D P 2021 J. Adv. Manuf. Technol. 114 3419
Google Scholar
[32] Wang Y Y, Zhang Y L, Tan D P 2021 Chinese J. Mech. Eng. 34 30
Google Scholar
[33] Ahmadi M H B, Yang Z Y 2020 Energy 207 118167
Google Scholar
[34] Kaiser J M J, Adami S, Akhatov I S, Adams N A 2020 Int. J. Heat Mass Transf. 155 119800
Google Scholar
[35] Meng Q F, Wu C Q, Su Y, Li J, Pang J B 2019 J. Clean. Prod. 210 1150
Google Scholar
[36] Deshpande S S, Trujillo M F, Wu X, Chahine G 2012 Int. J. Heat Fluid Flow 34 1
Google Scholar
[37] Yin Z C, Wan Y H, Fang H, Li L, Wang T, Wang Z, Tan DP 2022 Appl. Intel. DOI: 10.1007/s10489-022-04226-4 (in Press)
[38] Wang T, Li L, Yin Z C, Xie Z W, Wu J F, Zhang Y C, Tan D P 2022 P. I. Mech. Eng. C J. Mec. 236 11196
Google Scholar
[39] Li L, Lu J F, Fang H, Yin Z C, Wang T, Wang R H, Fan X H, Zhao L J, Tan D P, Wan Y H 2020 IEEE Access 8 27649
Google Scholar
[40] Park I S, Sohn C H 2011 Int. Commun. Heat Mass Transf. 38 1044
Google Scholar
-
图 1 含自由界面的多相流体示意图
Fig. 1. Schematic diagram of multiphase fluid with a free interface.
图 5 流体力学模型与边界条件 (a) 流体域模型; (b) 区域A的局部视角; (c) 区域B的局部视角; (d) 容器顶部视角. 1-入口壁面; 2-固定壁面; 3-出口壁面
Fig. 5. Fluid dynamic mechanic model and boundary conditions: (a) Fluid-domain model; (b) local view of region A; (c) local view of region B; (d) top view of the container. 1-inlet wall; 2-fixed wall; 3-out wall.
图 6 二维驻波算例验证 (a) 驻波; (b) 表面高度的衰减.
Fig. 6. Validation of the two-dimensional standing wave: (a) Standing wave; (b) decay of the surface elevation.
图 7 旋涡动力学模型验证 (a) 网格无关性; (b) CLSVOF与VOF模型的液位高度验证
Fig. 7. Validation of the vortex dynamic model: (a) Mesh independence; (b) liquid level height validation of the CLSVOF and VOF models.
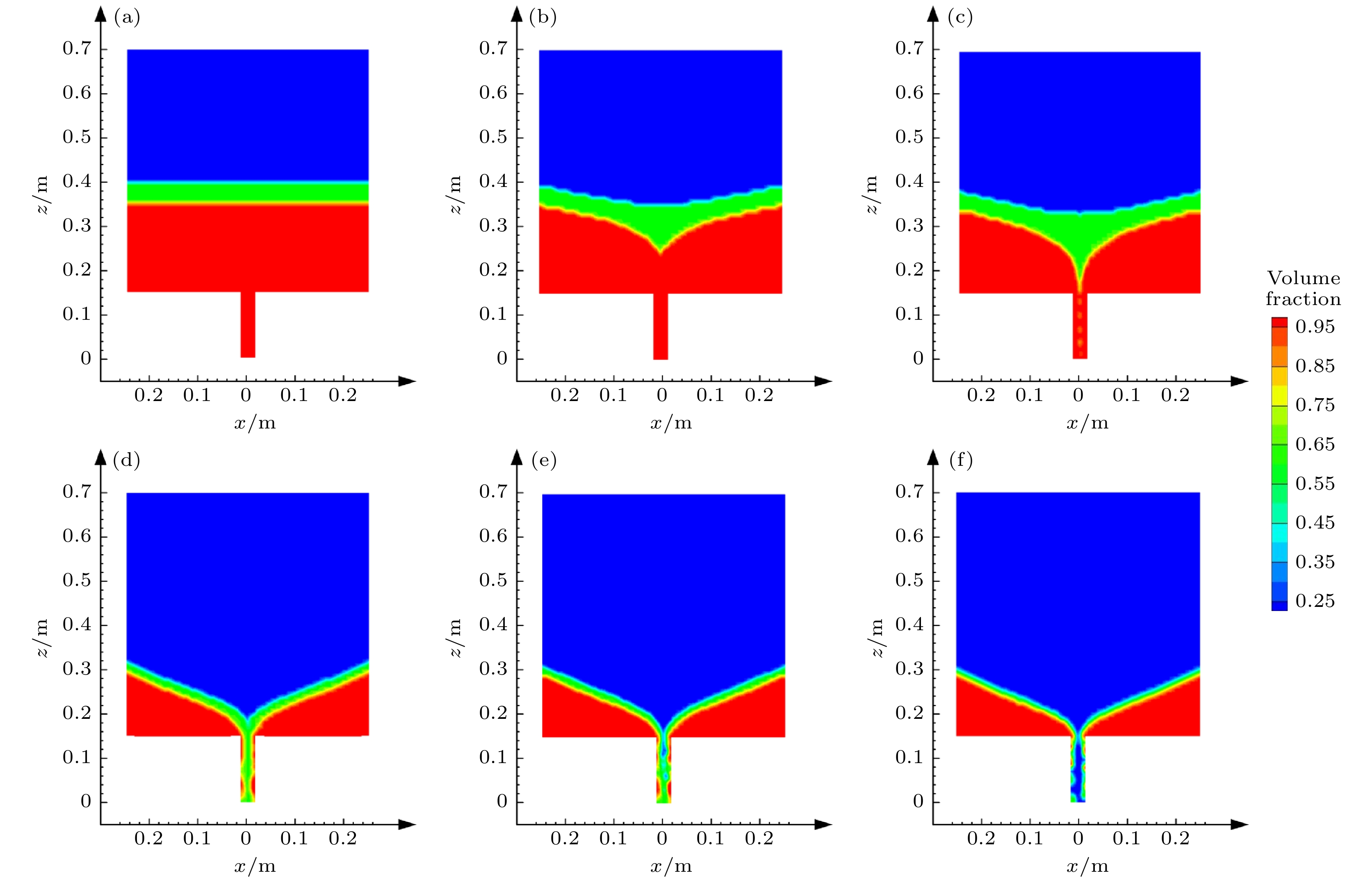
图 8 含自由液面的汇流旋涡体积分数云图 (a) t = 1.00 s; (b) t = 3.50 s; (c) t = 6.00 s; (d) t = 21.50 s; (e) t = 23.00 s; (f) t = 25.00 s
Fig. 8. Volume fraction cloud chart of the sink vortex with a free-liquid surface (ω0 = 1.0π rad/s): (a) t = 1.00 s; (b) t = 3.50 s; (c) t = 6.00 s; (d) t = 21.50 s; (e) t = 23.00 s; (f) t = 25.00 s.
图 9 旋涡流场的油相三维形貌图 (a) 凸点形成; (b) 油相抽吸; (c) 多相耦合输运; (d) 油相体积分数
Fig. 9. Three-dimensional morphology of oil-phase in the vortex flow field: (a) Salient point formation; (b) oil-phase suction; (c) multiphase coupling transport; (d) volume fraction of the oil phase.
图 10 旋涡多相耦合输运流线图 (a) t = 1.00 s; (b) t = 3.50 s; (c) t = 6.00 s; (d) t = 21.50 s; (e) t = 23.00 s; (f) t = 25.00 s
Fig. 10. Transport streamline chart of the vortex multiphase coupling: (a) t = 1.00 s; (b) t = 3.50 s; (c) t = 6.00 s; (d) t = 21.50 s; (e) t = 23.00 s; (f) t = 25.00 s.
图 11 不同水口尺度条件下的旋涡多相耦合输运流线图 (a) 0.73D*; (b) 0.87D*; (c) 1.00D*; (d) 1.13D*
Fig. 11. Transport streamline chart of the vortex multiphase coupling under different nozzle diameter: (a) 0.73D*; (b) 0.87D*; (c) 1.00D*; (d) 1.13D*.
图 13 旋涡流场的关键流动特性 (a) 切向速度分布; (b) 湍动能分布; (c) 涡量; (d) 动压.
Fig. 13. Key flow characteristics of the vortex flow field: (a) Tangential velocity distribution; (b) turbulent energy distribution; (c) vorticity; (d) dynamic pressure.
图 14 排流过程的总压变化曲线 (a) 总压曲线; (b) 总压云图
Fig. 14. Total pressure variation curves at the whole drain process: (a) Total pressure curve; (b) cloud diagram of the total pressure.
表 1 流体动力学模型的边界条件.
Table 1. Boundary conditions of the fluid dynamic model.
项 属性 入口 零法向梯度压力入口 出口 无回流平均压力出口 壁面 无滑移壁面(流体在壁面处的
速度或相对速度为零)重力/N 9.81 重力方向 z轴负方向 水相高度/m 0.2 气相高度/m 0.3 油相高度/m 0.05 
下载: 导出CSV
表 2 流体介质的物理参数.
Table 2. Physical parameters of fluid mediums.
介质 密度/
(kg·m–3)运动黏度/
(m2·s–1)动力黏度/
(Pa·s)表面张力/
(N·m–1)接触角/(°) 温度/
℃水 998.2 1.01×10–6 1.01×10–3 1.8×10–2 (油水) 135 20 油 730 1.01×10–6 2.4×10–3 2.6×10–2 (油气) 135 20 空气 1.225 1.48×10–5 1.79×10–5 7.3×10–2 (水气) 135 20
下载: 导出CSV
-
[1] Li L, Tan D P, Yin Z C, Wang T, Fan X H, Wang R H 2021 Renew. Energ. 175 887
Google Scholar
[2] Tan D P, Li L, Yin Z C, Li D F, Zhu Y L, Zheng S 2021 Int. J. Heat Mass Transfer. 150 119250
Google Scholar
[3] 谭大鹏, 杨涛, 赵军 2016 65 054701
Google Scholar
Tan D P, Tao Y, Zhao J 2016 Acta Phys. Sin. 65 054701
Google Scholar
[4] Li L, Tan D P, Wang T, Yin Z C, Fan X H, Wang R H 2021 Energy 216 119136
Google Scholar
[5] Aboelkassem Y, Georgicis V 2007 J. Fluids Eng. Trans. ASME 129 1073
Google Scholar
[6] Chen Y C, Huang S L, Li Z Y, Chang C C, Chu C C 2013 J. Fluid Mech. 733 134
Google Scholar
[7] Tan Y F, Ni Y S, Wu J F, Li L, Tan D P 2023 Int. J. Adv. Manuf. Technol. DOI: 10.1007/s00170-022-10761-8 (in Press)
[8] Tahershamsi A, Rahimzadeh H, Monshizadeh M, Sarkardeh H 2018 Meccanica 53 3269
Google Scholar
[9] Tan D P, Ni Y S, Zhang L B 2017 J. Iron Steel Res. Int. 24 669
Google Scholar
[10] Morales R D, Dávila–Maldonado O, Calderón I 2013 ISIJ Int. 53 782
Google Scholar
[11] Yang M, Liu S, Xu W H 2020 ACS Omega 5 31332
Google Scholar
[12] Škerlavaj A, Škerget L, Ravnik J 2014 Eng. Appl. Comp. Fluid Mech. 8 193
Google Scholar
[13] Ahn S H, Xiao Y X, Wang Z W, Zhou X Z, Luo Y Y 2017 Renew. Energ. 101 617
Google Scholar
[14] Li L, Qi H, Yin Z C, Li D F, Zhu Z L, Tangwarodomnukun V, Tan D P 2020 Powder Technol. 360 462
Google Scholar
[15] Zheng G A, Gu Z H, Xu W X, Li Q H, Tan Y F, Wang C Y, Li L 2023 Proesses 11 42
Google Scholar
[16] Ling K, Zhang S, Wu P Z, Yang S Y, Tao W Q 2019 Int. J. Heat Mass Transf. 143 118565
Google Scholar
[17] Tan D P, Li L, Zhu Y L, Zheng S, Yin Z C, Li D F 2019 J. Zhejiang Univ.-SCI A 20 61
Google Scholar
[18] 谭大鹏, 计时鸣, 李培玉 2010 中国科学-技术科学 53 2378
Google Scholar
Tan D P, Ji S M, Li P Y 2010 Sci. China-Technol. Sci. 53 2378
Google Scholar
[19] Duan G T, Chen B, Zhang X M, Wang Y C 2017 Comput. Method Appl. Eng. 320 133
Google Scholar
[20] Qian J Y, Zhao L, Li X J, Li Q Q, Jin Z J 2022 J. Zhejiang Univ.-SCI A. 23 783
Google Scholar
[21] Tan D P, Li L, Zhu Y L, Zheng S, Ruan H J, Jiang X Y 2018 IEEE Trans. Ind. Inform. 14 2881
Google Scholar
[22] Wang J X, Gao S B, Tang Z J, Tan D P 2021 J. Intell.Manuf. DOI: 10.1007/s10845-021-01854-4 (in Press)
[23] Tan D P, Zhang L B 2014 Sens. Actuator. B 202 1257
Google Scholar
[24] Pan Y, Ji S M, Tan D P, Cao H Q 2020 Int. J. Manuf. Technol. 109 2587
Google Scholar
[25] Li L, Yang Y S, Xu W X, Lu B, Gu Z H, Yang J G, Tan D P 2021 Appl. Sci. 12 8538
Google Scholar
[26] Yin Z C, Ni Y S, Li L, Wang T, Wu J F, Li Z, Tan D P 2022 J. Zhejiang Univ.-SCI A DOI: 10.1631/jzus.A2200014 (in Press)
[27] Li L, Xu W X, Tan Y F, Yang Y S, Yang J G, Tan D P 2023 Mech. Syst. Signal Process 189 110058
Google Scholar
[28] Gen J Q, Ji S M, Tan D P 2018 J. Adv. Manuf. Technol. 95 1069
Google Scholar
[29] Ruan Y M, Yao Y, Shen S Y, Wang B, Wang B, Zhang J Y, Huang J K 2020 Steel Res. Int. 91 1900616
Google Scholar
[30] Zheng S H Yu Y K, Qiu M Z, Wang L M, Tan D P 2021 Appl. Math. Model. 91 934
Google Scholar
[31] Ge M, Ji S M, Tan D P 2021 J. Adv. Manuf. Technol. 114 3419
Google Scholar
[32] Wang Y Y, Zhang Y L, Tan D P 2021 Chinese J. Mech. Eng. 34 30
Google Scholar
[33] Ahmadi M H B, Yang Z Y 2020 Energy 207 118167
Google Scholar
[34] Kaiser J M J, Adami S, Akhatov I S, Adams N A 2020 Int. J. Heat Mass Transf. 155 119800
Google Scholar
[35] Meng Q F, Wu C Q, Su Y, Li J, Pang J B 2019 J. Clean. Prod. 210 1150
Google Scholar
[36] Deshpande S S, Trujillo M F, Wu X, Chahine G 2012 Int. J. Heat Fluid Flow 34 1
Google Scholar
[37] Yin Z C, Wan Y H, Fang H, Li L, Wang T, Wang Z, Tan DP 2022 Appl. Intel. DOI: 10.1007/s10489-022-04226-4 (in Press)
[38] Wang T, Li L, Yin Z C, Xie Z W, Wu J F, Zhang Y C, Tan D P 2022 P. I. Mech. Eng. C J. Mec. 236 11196
Google Scholar
[39] Li L, Lu J F, Fang H, Yin Z C, Wang T, Wang R H, Fan X H, Zhao L J, Tan D P, Wan Y H 2020 IEEE Access 8 27649
Google Scholar
[40] Park I S, Sohn C H 2011 Int. Commun. Heat Mass Transf. 38 1044
Google Scholar
下载:
计量
- 文章访问数: 4158
- PDF下载量: 87
- 被引次数: 0
