-
内孤立波在海洋中广泛存在, 其在生成、传播演化以及耗散过程中对海洋环境、地形地貌和海洋结构物等有着深远的影响. 针对内孤立波理论模型研究, 已有理论模型包括单向传播Korteweg-de Vries (KdV) 类方程和双向传播Miyata-Choi-Camassa (MCC) 类方程, 然而, 两类方程均未能有效地模拟大振幅内孤立波的传播演化过程. 本文采用渐近匹配方法, 对原始单向传播内孤立波方程的系数进行修正, 建立了改进的单向传播内孤立波理论模型. 在此基础上, 通过比较分析改进了前后内孤立波的理论模型, 结果表明, 改进后的理论模型稳态内孤立波的理论极限振幅能达到MCC 方程稳态内孤立波的理论极限振幅. 结合系列实验结果, 通过定量分析稳态内孤立波有效波长、波速和波形与MCC 方程稳态内孤立波理论解的吻合度, 进一步分析了改进后的内孤立波理论模型在表征定态内孤立波特性方面的适用性. 此外, 针对平坦地形条件下大振幅内孤立波非定态传播演化过程, 探究各类单向传播孤立波理论模型的稳定性. 研究表明改进后高阶单向传播内孤立波理论模型可用于表征大振幅内孤立波传播演化特性, 为海洋结构物水动力学研究提供理论依据.Internal solitary waves exist widely in the oceans, and their generations, propagation evolutions, and dissipations have profound effects on the ocean environment, topography, and marine structures. Typically, two basic theoretical models are now being developed to govern the evolutions of internal solitary waves at the interface of two immiscible inviscid fluids. One is a unidirectional wave propagation model described by the KdV (Korteweg-de Vries) equation, and the other is a bidirectional wave propagation model depicted by the Miyata-Choi-Camassa (MCC) equation. Neither of them, however, can effectively characterize the course of the evolution of large-amplitude internal solitary wave. In this paper, a modified unidirectional internal solitary wave model is established by adjusting the coefficients of the original unidirectional model. The adjusted coefficients are determined through asymptotic analysis by matching with the MCC model. The efficacy of the modified coefficients is investigated by comparing the modified model with the original model. The experiments on the generation of internal solitary waves with varying amplitudes are carried out by comparing the internal solitary wave solution of the modified equation. It is shown that the modified model is suitable for describing the waveform of internal solitary waves with small, medium, and large amplitudes within the limiting amplitude of the MCC model. By quantitatively analyzing the agreement of the effective wavelength, wave speed, and waveform of steady-state internal solitary waves between the unidirectional model and the MCC model, the applicability of the modified model in characterization of the properties of steady-state internal solitary waves is further investigated. In addition, the stability of unidirectional theoretical model is analyzed for simulating the propagation of large-amplitude internal solitary wave under flat bottom condition. It is found that the unidirectional model is suitable for initiating its own internal solitary solution provided that the numerical scheme is stable. It is shown that the modified unidirectional model can be used to characterize large-amplitude internal solitary waves, and is also expected to be applied to the study of marine structure hydrodynamics.
-
Keywords:
- internal solitary waves /
- theoretical model /
- two-layer fluid /
- strong nonlinerity
[1] Cai S, Xie J, He J 2012 Surv. Geophys. 33 927
Google Scholar
[2] Alford, H M, Lien, Ren-Chieh, Simmons, Harper, Klymak, Jody, Ramp, Steve, Yang, Jang Y, Tang, David, Chang, Ming-Huei 2010 J. Phys. Oceanogr. 40 1338
[3] Klymak J M, Pinkel R, Liu C T, Liu A K, David L 2006 Geophys. Res. Lett. 33 L11607
[4] Huang X, Chen Z, Zhao W, Zhang Z, Zhou C, Yang Q, Tian J 2016 Sci. Rep. 6 1
Google Scholar
[5] Alford M H, Peacock T, MacKinnon J A, Nash J D, Buijsman M C, Centurioni L R, Chao S Y, Chang M H, Farmer D M, Fringer O B 2015 Nature 521 65
Google Scholar
[6] Holloway P E, Pelinovsky E, Talipova T 1999 J. Geophys. Res. Oceans 104 18333
Google Scholar
[7] Holloway P E, Pelinovsky E, Talipova T, Barnes B 1997 J. Phys. Oceanogr. 27 871
Google Scholar
[8] 郅长红, 陈科, 尤云祥 2021 上海交通大学学报 55 916
Google Scholar
Zhi C, Chen K, You Y 2021 J. Shanghai Jiaotong Univ. Sci. 55 916
Google Scholar
[9] Zhi C, Chen K, You Y 2018 J. Ocean Eng. Sci. 3 83
Google Scholar
[10] Zou L, Du B Y, Ma X Y, Li Z H, Zhang Z H 2019 Chinese Congress of Theoretical and Applied Mechanics. Hangzhou, Zhejiang, China, August 25–28, 2019 p13
[11] Miyata M 1985 Lamer 23 43
[12] Miyata M 1988 Nonlinear water waves (Springer) pp399–406
[13] Choi W, Camassa R 1999 J. Fluid Mech. 396 1
Google Scholar
[14] Michallet H, Barthelemy E 1998 J. Fluid Mech. 366 159
Google Scholar
[15] Ostrovsky L A, Grue J 2003 Phys. Fluids 15 2934
Google Scholar
[16] Zhao B, Wang Z, Duan W, Ertekin R C, Hayatdavoodi M, Zhang T 2020 J. Fluid Mech. 899 A17
Google Scholar
[17] Kodaira T, Waseda T, Miyata M, Choi W 2016 J. Fluid Mech. 804 201
Google Scholar
[18] Choi W, Camassa R 1996 J. Fluid Mech. 313 83
Google Scholar
[19] Choi W, Zhi C, Barros R 2020 Ocean Model. 151 101643
Google Scholar
[20] Jo T C, Choi W 2002 Stud. Appl. Math. 109 205
Google Scholar
[21] Zhi C H, Wang H, Chen K, You Y X 2021 Ocean Eng. 223 108645
Google Scholar
[22] 郅长红, 陈科, 尤云祥 2021 水动力学研究与进展(A辑) 36 395
Google Scholar
Zhi C H, Chen K, You Y X 2021 Chinese J. Hydrodyn. 36 395
Google Scholar
[23] 黄文昊, 尤云祥, 王旭, 胡天群 2013 62 084705
Google Scholar
Huang W H, You Y X, Wang X, Hu T Q 2013 Acta Phys. Sin. 62 084705
Google Scholar
-
图 1 aHOU, HOU, MCC方程 (a) 线性速度
${c_{{\text{lin}}}}/(gh)$ 随$kh$ 的变化; (b)$kh$ 随波幅的变化Fig. 1. aHOU, HOU and MCC models: (a) The variation of the linear speed
${c_{{\text{lin}}}}/(gh)$ with$kh$ ; (b) the variation of$kh$ with amplitude.
图 3 KdV, eKdV, MCC和aHOU理论波形与实验波形的比较 (a) a/h = –0.2028; (b) a/h = –0.1362; (c) a/h = –0.0584
Fig. 3. Comparison of theoretical and experimental waveforms for KdV, eKdV, MCC and aHOU models: (a) a/h = –0.2028; (b) a/h = –0.1362; (c) a/h = –0.0584.
图 4 KdV, eKdV, aHOU与MCC方程的稳态内孤立波 (a) 有效波长
$\lambda /h$ 随振幅$|a|/h$ 的变化; (b) 波速$c/{c_0}$ 随振幅$|a|/h$ 的变化Fig. 4. Variation characteristics for KdV, eKdV, aHOU and MCC models: (a) The effective wavelength
$\lambda /h$ with amplitude$|a|/h$ ; (b) the wave speed$c/{c_0}$ with amplitude$|a|/h$ .
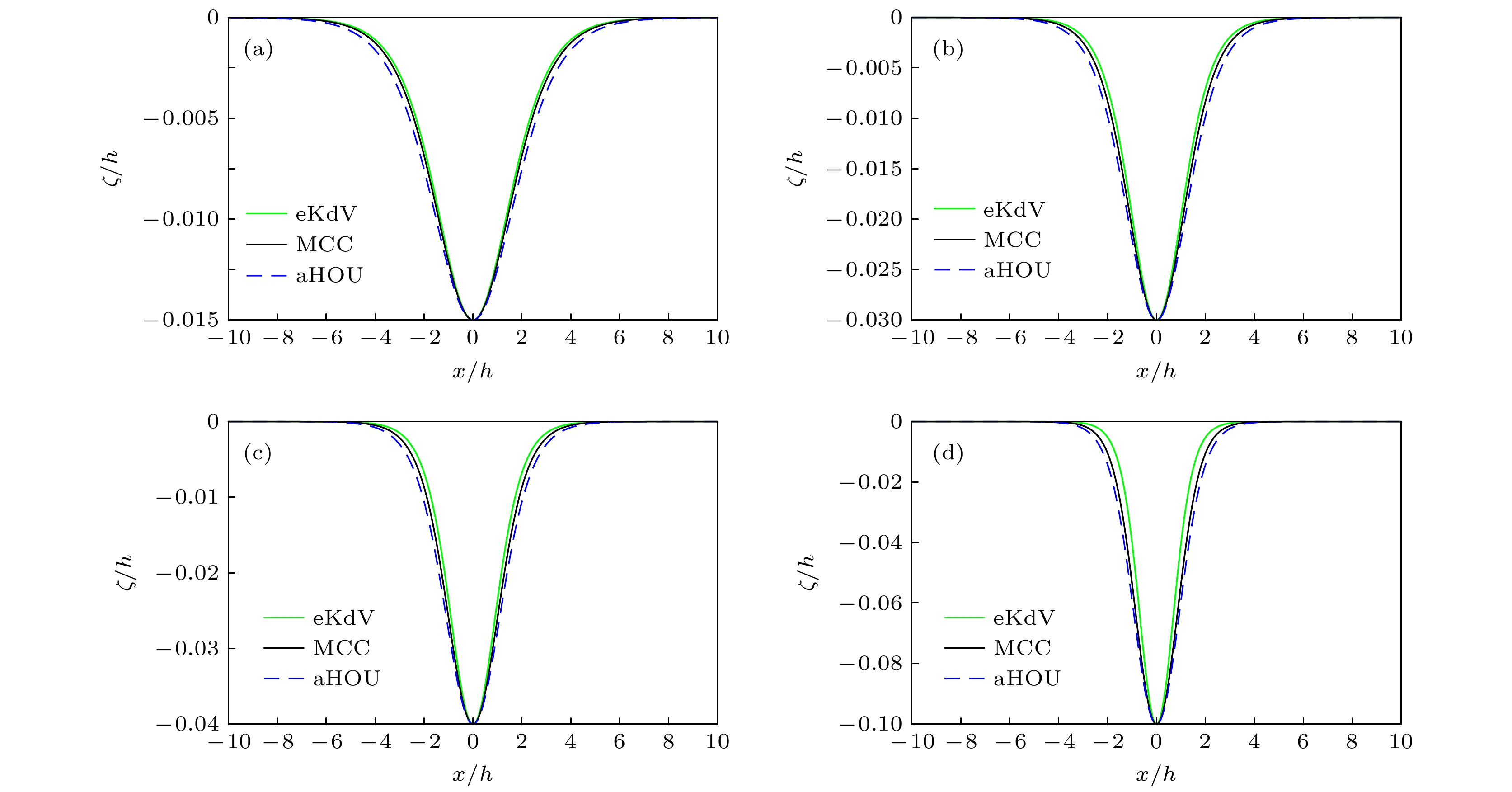
图 5 KdV型稳态内孤立波与eKdV, aHOU和MCC型方程稳态内孤立波波形的比较 (a)
$|a|/h$ = 0.010; (b)$|a|/h$ = 0.015; (c)$|a|/h$ = 0.020; (d)$|a|/h$ = 0.100Fig. 5. Comparison of steady-state internal solitary waveform of KdV, eKdV, aHOU and MCC models: (a)
$|a|/h$ = 0.010; (b)$|a|/ h$ = 0.015; (c)$|a|/h$ = 0.020; (d)$|a|/h$ = 0.100.
图 6 eKdV型稳态内孤立波与aHOU和MCC型方程稳态内孤立波波形的比较 (a)
$|a|/h$ = 0.015; (b)$|a|/h$ = 0.030; (c)$|a|/ h$ = 0.040; (d)$|a|/h$ = 0.100Fig. 6. Comparison of steady-state internal solitary waveform of eKdV, aHOU and MCC models: (a)
$|a|/h$ = 0.015; (b)$|a|/h$ = 0.030; (c)$|a|/h$ = 0.040; (d)$|a|/h$ = 0.100.
图 7 aHOU型稳态内孤立波与MCC型方程稳态内孤立波波形的比较 (a)
$|a|/h$ = 0.015; (b)$|a|/h$ = 0.030; (c)$|a|/h$ = 0.070; (d)$|a|/h$ = 0.110; (e)$|a|/h$ = 0.150; (f)$|a|/h$ = 0.290Fig. 7. Comparison of the steady-state internal solitary waveform between aHOU and MCC models: (a)
$|a|/h$ = 0.015; (b)$|a|/h$ = 0.030; (c)$|a|/h$ = 0.070; (d)$|a|/h$ = 0.110; (e)$|a|/h$ = 0.150; (f)$|a|/h$ = 0.290.
图 8 当
$0 \leqslant t{(h/g)^{1/2}} \leqslant 3000$ 时,$ - \zeta /h$ 随$t{(h/g)^{1/2}}$ 的变化特性 (a) aHOU方程; (b) eKdV方程; (c) KdV方程Fig. 8. Variation characteristics of
$ - \zeta /h$ with$t $ $ {(h/g)^{1/2}}$ when$0 \leqslant t{(h/g)^{1/2}} \leqslant 3000$ : (a) aHOU model; (b) eKdV model; (c) KdV model.表 1 三类孤立波理论稳态解波形的契合度
Table 1. Waveform fitness of three theoretical models
|a|/h $\varDelta $aHOU $\varDelta $eKdV $\varDelta $KdV 0.010 0.0702 0.0273 0.0459 0.015 0.0748 0.0402 0.0681 0.020 0.0780 0.0549 0.0931 0.025 0.0809 0.0650 0.1121 0.030 0.0828 0.0743 0.1314 0.035 0.0836 0.0852 0.1483 0.040 0.0868 0.0981 0.17197 0.045 0.0883 0.1074 0.1908 0.050 0.0879 0.1135 0.2029 0.070 0.0912 0.1494 0.2775 0.080 0.0914 0.1597 0.3037 0.090 0.0791 0.1709 0.3308 0.100 0.0878 0.1803 0.3607 0.110 0.0895 0.1888 0.3908 0.120 0.0866 0.1941 0.4143 0.130 0.0840 0.2006 0.4464 0.140 0.0842 0.2009 0.4727 0.150 0.0818 0.1972 0.4921 0.200 0.0708 0.0950 0.6075 0.250 0.0876 — — 0.260 0.0604 — — 0.270 0.0588 — — 0.280 0.0567 — — 0.290 0.0525 — — 
下载: 导出CSV
-
[1] Cai S, Xie J, He J 2012 Surv. Geophys. 33 927
Google Scholar
[2] Alford, H M, Lien, Ren-Chieh, Simmons, Harper, Klymak, Jody, Ramp, Steve, Yang, Jang Y, Tang, David, Chang, Ming-Huei 2010 J. Phys. Oceanogr. 40 1338
[3] Klymak J M, Pinkel R, Liu C T, Liu A K, David L 2006 Geophys. Res. Lett. 33 L11607
[4] Huang X, Chen Z, Zhao W, Zhang Z, Zhou C, Yang Q, Tian J 2016 Sci. Rep. 6 1
Google Scholar
[5] Alford M H, Peacock T, MacKinnon J A, Nash J D, Buijsman M C, Centurioni L R, Chao S Y, Chang M H, Farmer D M, Fringer O B 2015 Nature 521 65
Google Scholar
[6] Holloway P E, Pelinovsky E, Talipova T 1999 J. Geophys. Res. Oceans 104 18333
Google Scholar
[7] Holloway P E, Pelinovsky E, Talipova T, Barnes B 1997 J. Phys. Oceanogr. 27 871
Google Scholar
[8] 郅长红, 陈科, 尤云祥 2021 上海交通大学学报 55 916
Google Scholar
Zhi C, Chen K, You Y 2021 J. Shanghai Jiaotong Univ. Sci. 55 916
Google Scholar
[9] Zhi C, Chen K, You Y 2018 J. Ocean Eng. Sci. 3 83
Google Scholar
[10] Zou L, Du B Y, Ma X Y, Li Z H, Zhang Z H 2019 Chinese Congress of Theoretical and Applied Mechanics. Hangzhou, Zhejiang, China, August 25–28, 2019 p13
[11] Miyata M 1985 Lamer 23 43
[12] Miyata M 1988 Nonlinear water waves (Springer) pp399–406
[13] Choi W, Camassa R 1999 J. Fluid Mech. 396 1
Google Scholar
[14] Michallet H, Barthelemy E 1998 J. Fluid Mech. 366 159
Google Scholar
[15] Ostrovsky L A, Grue J 2003 Phys. Fluids 15 2934
Google Scholar
[16] Zhao B, Wang Z, Duan W, Ertekin R C, Hayatdavoodi M, Zhang T 2020 J. Fluid Mech. 899 A17
Google Scholar
[17] Kodaira T, Waseda T, Miyata M, Choi W 2016 J. Fluid Mech. 804 201
Google Scholar
[18] Choi W, Camassa R 1996 J. Fluid Mech. 313 83
Google Scholar
[19] Choi W, Zhi C, Barros R 2020 Ocean Model. 151 101643
Google Scholar
[20] Jo T C, Choi W 2002 Stud. Appl. Math. 109 205
Google Scholar
[21] Zhi C H, Wang H, Chen K, You Y X 2021 Ocean Eng. 223 108645
Google Scholar
[22] 郅长红, 陈科, 尤云祥 2021 水动力学研究与进展(A辑) 36 395
Google Scholar
Zhi C H, Chen K, You Y X 2021 Chinese J. Hydrodyn. 36 395
Google Scholar
[23] 黄文昊, 尤云祥, 王旭, 胡天群 2013 62 084705
Google Scholar
Huang W H, You Y X, Wang X, Hu T Q 2013 Acta Phys. Sin. 62 084705
Google Scholar
下载:
计量
- 文章访问数: 5285
- PDF下载量: 89
- 被引次数: 0
