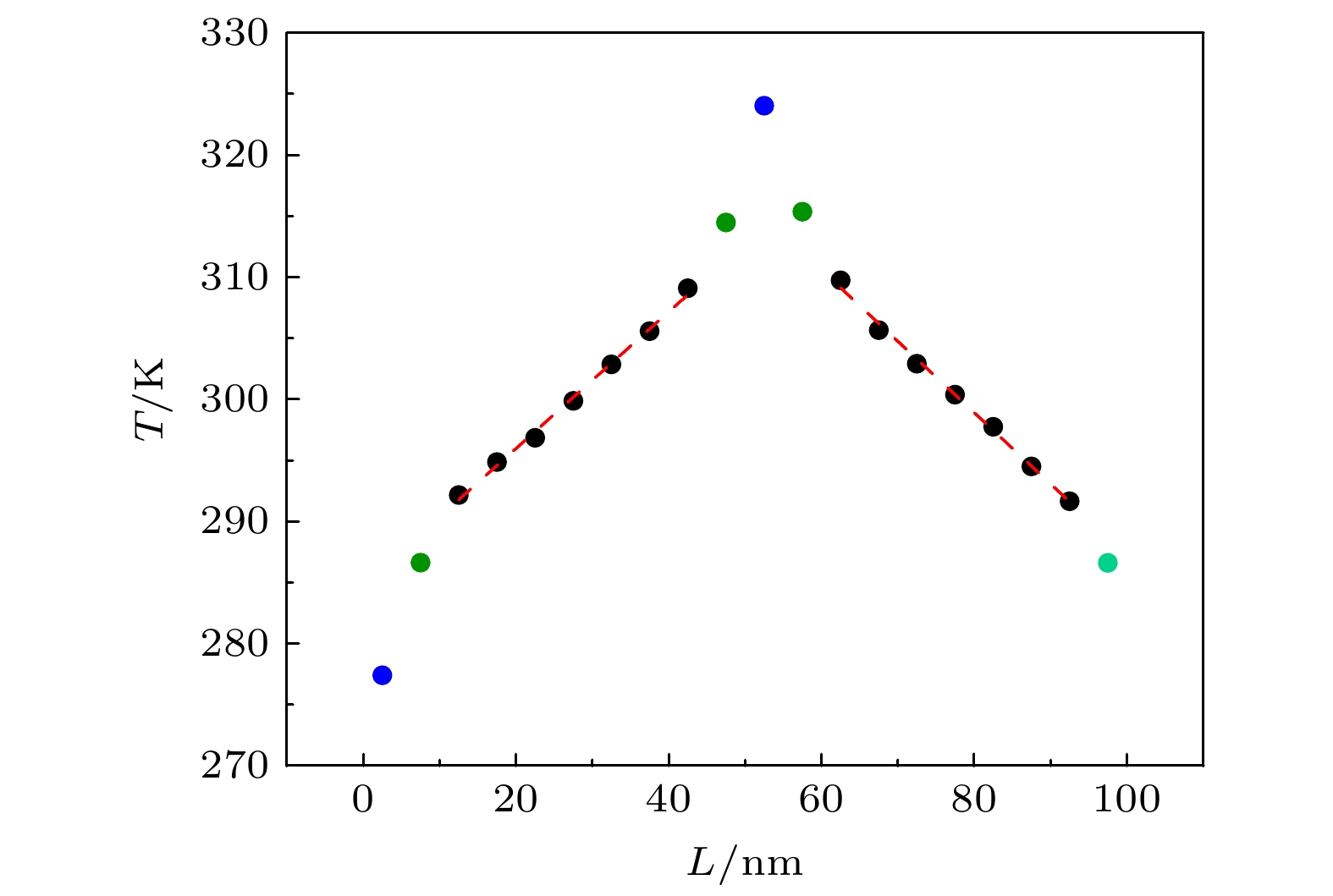
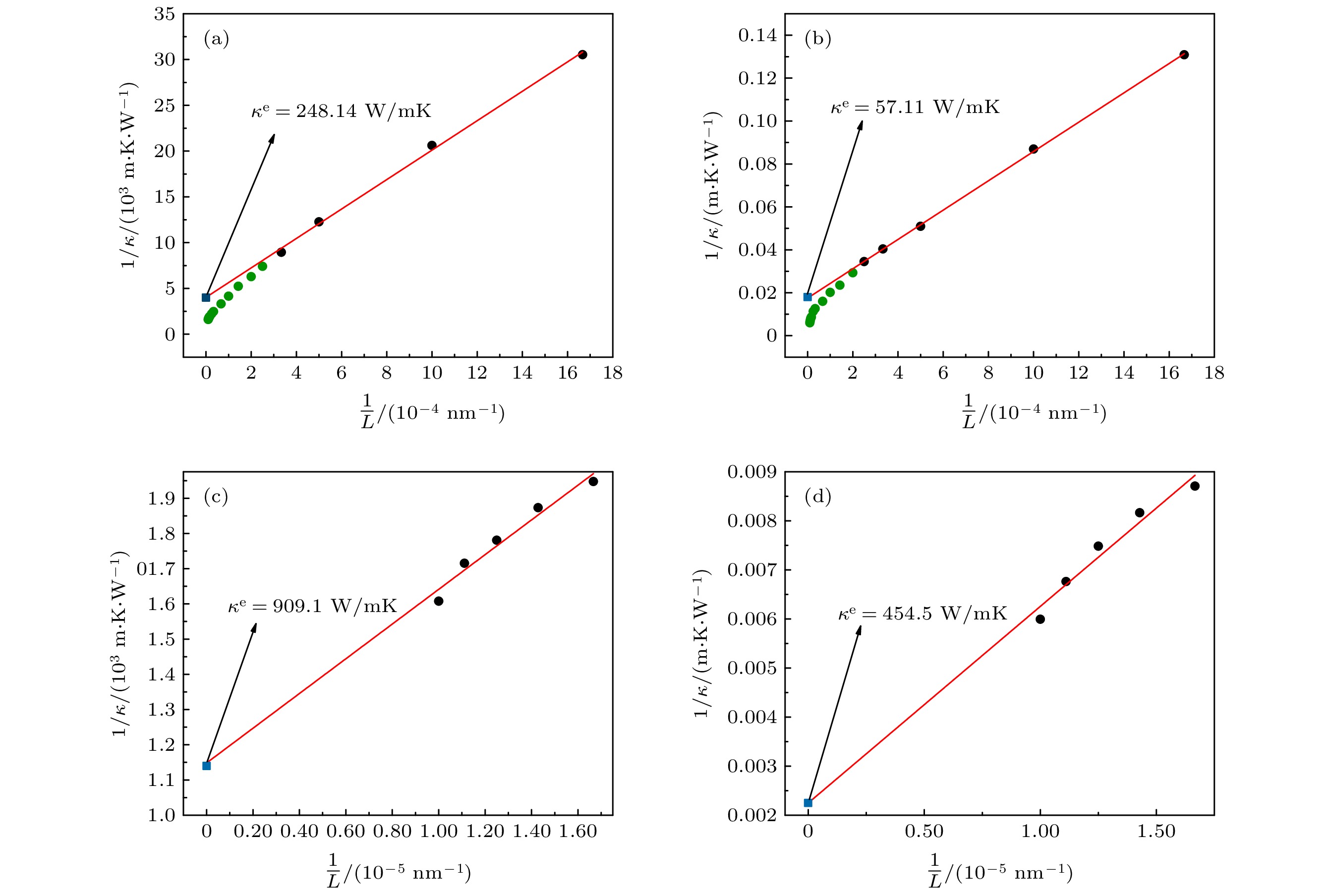
-
采用Tersoff势测试和研究了反向非平衡分子动力学中的Müller-Plathe法和Jund法在一维纳米管热传导中的应用. 在相同的模拟步数中, Müller-Plathe法可以得到很好的结果, 热导率在交换频率大于50时对参数的选择并不敏感. 然而, Jund法并不能得到良好的线性温度梯度, 其热导率在一定程度上依赖于选择的热流大小. 在此基础上, 运用Müller-Plathe法进一步研究了碳纳米管和碳化硅纳米管的长度、直径和温度对热导率的影响. 结果表明, 无论是碳纳米管还是碳化硅纳米管, 其长度、直径和温度对热导率的影响是一致的. 只要长度增加, 纳米管的热导率相应增大, 但增长速率不断降低. 直径对热导率的影响很大程度上还取决于温度, 在高温时, 直径对热导率几乎没有影响. 除此之外, 纳米管的热导率随着温度的增加总体上也是不断降低的, 但峰值现象的出现还受纳米管长度的影响.
-
关键词:
- 反向非平衡分子动力学 /
- 热传导 /
- 碳纳米管 /
- 碳化硅纳米管
In this paper, the application of Muller-Plathe method and Jund method in reverse nonequilibrium molecular dynamics to the heat conduction of one-dimensional nanotubes are tested and studied. The results show that the Jund method cannot obtain a good linear temperature gradient and its thermal conductivity is also dependent on the choice of heat flux. When the exchange frequency is 50, the thermal conductivity obtained by the Muller-Plathe method converges to a stable value. This method can be well applied to the study of thermal conductivity of nanotubes. The Muller-Plathe method is a good option when the number of atoms exchanged is 1 and the exchange frequency is 100. On this basis, we further investigate the effect of length, diameter and temperature of carbon nanotubes and silicon carbide nanotubes on the thermal conductivity. The thermal conductivity of carbon nanotubes is obviously higher than that of silicon carbide nanotubes, and their effects of length, diameter and temperature on the thermal conductivity are consistent. The thermal conductivity of nanotubes increases with the rise of temperature, but the increase rate decreases and the length dependence also weakens. Therefore, when carbon nanotubes and silicon carbide nanotubes reach certain lengths, their values of thermal conductivity will converge and no longer change with length, which is completely consistent with the results of previous studies. Comparing with carbon nanotubes, the convergence rate of thermal conductivity of SiC nanotubes is significantly lower. When the temperature is low, the diameter has a certain effect on the thermal conductivity; however, with the increase of temperature, the diameter has almost no effect on the thermal conductivity at high temperature. The effect of temperature on the thermal conductivity of nanotubes shows that the thermal conductivity of nanotubes generally decreases with the rise of temperature, but the occurrence of the peak phenomenon is also affected by the length of nanotubes. When the length of carbon nanotubes is 10 nm, the influence of temperature and diameter on the thermal conductivity are irregular. However, when the length of carbon nanotubes is 100 nm, the thermal conductivity of carbon nanotubes decreases continuously with the rise of temperature, and there occurs no peak phenomenon. Besides, when the tube length is 10 nm, the peak of SiC nanotubes appears at about 100 K. However, when the tube length is 100 nm, the thermal conductivity of SiC nanotubes decreases with the rise of temperature, but no peak phenomenon occurs.-
Keywords:
- reverse nonequilibrium molecular dynamics /
- heat conduction /
- carbon nanotubes /
- silicon carbide nanotubes
[1] Ouyang Y L, Zhang Z W, Li D F, Chen J, Zhang G 2019 Ann. Phys. 531 1800437
Google Scholar
[2] Zhang Z, Ouyang Y, Cheng Y, Chen J, Li N, Zhang G 2020 Phys. Rep. 860 1
Google Scholar
[3] Ren W, Ouyang Y, Jiang P, Yu C, He J, Chen J 2021 Nano Lett. 21 2634
Google Scholar
[4] Yang N, Xu X, Zhang G, Li B 2012 AIP Adv. 2 041410
Google Scholar
[5] Zhang R, Lee S, Law C K, Li W K, Teo B K 2002 Chem. Phys. Lett. 364 251
Google Scholar
[6] Durgun E, Tongay S, Ciraci S 2005 Phys. Rev. B 72 075420
Google Scholar
[7] He T, Zhao M, Li W, Lin X, Zhang X, Liu X, Xia Y, Mei L 2008 Nanotechnology 19 205707
Google Scholar
[8] Menon M, Richter E, Mavrandonakis A, Froudakis G, Andriotis A N 2004 Phys. Rev. B 69 115322
Google Scholar
[9] Balandin A A 2011 Nat. Mater. 10 569
Google Scholar
[10] Berber S, Kwon Y K, Tomanek D 2000 Phys. Rev. Lett. 84 4613
Google Scholar
[11] Padgett C W, Brenner D W 2004 Nano Lett. 4 1051
Google Scholar
[12] Donadio D, Galli G 2007 Phys. Rev. Lett. 99 255502
Google Scholar
[13] Moreland J F 2004 Microscale Thermophys. Eng. 8 61
Google Scholar
[14] Lukes J R, Zhong H 2007 J. Heat Transfer 129 705
Google Scholar
[15] Zhang G, Li B 2005 J. Chem. Phys. 123 114714
Google Scholar
[16] Maruyama S 2002 Phys. B 323 193
Google Scholar
[17] Mingo N, Broido D A 2005 Nano Lett. 5 1221
Google Scholar
[18] Shiomi J, Maruyama S 2007 Thermal Engineering Summer Heat Transfer Conference Vancouver, British Columbia, Canada, July 8–12, 2007 p381
[19] Wang J, Wang J S 2006 Appl. Phys. Lett. 88 111909
Google Scholar
[20] Yao Z, Wang J S, Li B, Liu G R 2005 Phys. Rev. B 71 085417
Google Scholar
[21] 保文星, 朱长纯 2006 55 3552
Google Scholar
Bao W X, Zhu C C 2006 Acta Phys. Sin. 55 3552
Google Scholar
[22] 侯泉文, 曹炳阳, 过增元 2009 58 7809
Google Scholar
Hou Q W, Cao B Y, Guo Z Y 2009 Acta Phys. Sin. 58 7809
Google Scholar
[23] 王照亮, 梁金国, 唐大伟 2008 57 3391
Google Scholar
Wang Z L, Liang J G, Tang D W 2008 Acta Phys. Sin. 57 3391
Google Scholar
[24] Osman M A, Srivastava D 2001 Nanotechnology 12 21
Google Scholar
[25] Cao J X, Yan X H, Xiao Y, Ding J W 2004 Phys. Rev. B 69 073407
Google Scholar
[26] Maruyama S 2003 Microscale Thermophys. Eng. 7 41
Google Scholar
[27] Che J, Cagin T, Goddard III W A 2000 Nanotechnology 11 65
Google Scholar
[28] Bai D 2011 Fullerenes, Nanotubes, Carbon Nanostruct 19 271
Google Scholar
[29] Lyver J W, Blaisten-Barojas E 2011 J. Comput. Theor. Nanosci. 8 529
Google Scholar
[30] Shen H 2009 Comput. Mater. Sci. 47 220
Google Scholar
[31] Mingo N, Broido D A 2005 Phys. Rev. Lett. 95 096105
Google Scholar
[32] Chen J, Zhang G, Li B W 2010 J. Phys. Soc. Jpn. 79 074604
Google Scholar
[33] Müller-Plathe F 1997 J. Chem. Phys. 106 6082
Google Scholar
[34] Jund P, Jullien R 1999 Phys. Rev. B 59 13707
Google Scholar
[35] Nieto-Draghi C, Avalos J B 2009 Mol. Phys. 101 2303
[36] Zhang M, Lussetti E, de Souza L E, Muller-Plathe F 2005 J. Phys. Chem. B 109 15060
Google Scholar
[37] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[38] Tersoff J 1989 Phys. Rev. B 39 5566
Google Scholar
[39] Schelling P K, Phillpot S R, Keblinski P 2002 Phys. Rev. B 65 144306
Google Scholar
[40] Sellan D P, Landry E S, Turney J E, McGaughey A J H, Amon C H 2010 Phys. Rev. B 81 214305
Google Scholar
[41] Zhang W, Zhu Z, Wang F, Wang T, Sun L, Wang Z 2004 Nanotechnology 15 936
Google Scholar
-
图 2 纳米管轴向温度分布图(蓝点为热区和冷区; 绿点为温度跳变点; 黑点为线性反应区)
Fig. 2. Axial temperature distribution of nanotubes. The blue points are the hot and cold areas; the green point is the temperature jump point; the black dots are linear reaction zones.
图 3 6 nm碳纳米管在不同交换频率下温差随时间的变化图
Fig. 3. Temperature difference of 6 nm carbon nanotubes at different exchange frequencies changes with time.
图 4 (5, 5)纳米管热导率随长度的幂指数变化关系(T = 300 K, 图中用的是log-log坐标轴) (a)碳纳米管; (b)碳化硅纳米管
Fig. 4. Exponent variation of thermal conductivity of (5, 5) nanotubes with length (T = 300 K): (a) Carbon nanotubes; (b) silicon carbide nanotubes. The log-log axis are used.
图 5 (5, 5)纳米管热导率随长度的变化关系(T = 300 K) (a)碳纳米管; (b)碳化硅纳米管
Fig. 5. Variation of thermal conductivity of (5, 5) nanotubes with length (T = 300 K): (a) Carbon nanotubes; (b) SiC nanotubes.
图 6 (5, 5)纳米管1/κ随1/L的变化关系(T = 300 K) (a), (c)碳纳米管; (b), (d)碳化硅纳米管
Fig. 6. Variation of 1/κ with 1/L of (5, 5) nanotubes (T = 300 K): (a), (c) Carbon nanotubes; (b), (d) SiC nanotubes.
图 7 碳纳米管热导率的直径和温度的依赖关系(n是纳米管的手性参数) (a) L = 10 nm; (b) L = 100 nm
Fig. 7. Diameter and temperature dependence of the thermal conductivity of carbon nanotubes, where n is the chiral index of the nanotube: (a) L = 10 nm; (b) L = 100 nm
图 8 碳化硅纳米管热导率的直径和温度依赖关系 (a) L = 10 nm; (b) L = 100 nm
Fig. 8. Diameter and temperature dependence of the thermal conductivity of silicon carbide nanotubes: (a) L = 10 nm; (b) L = 100 nm
表 1 Müller-Plath法得到的热流和热导率(*代表温度梯度线性程度十分糟糕; 6, 20, 50是纳米管的长度(单位: nm))
Table 1. Heat flux and thermal conductivity obtained by Muller-Plath method. * represents a very poor linearity of the temperature gradient. 6, 20, 50 is the length of the nanotube (unit: nm).
频率 碳纳米管 碳化硅纳米管 热流/(eV·ps–1) 热导率/(W·m–1·K–1) 热流/(eV·ps–1) 热导率/(W·m–1·K–1) 6 20 50 6 20 50 6 20 50 6 20 50 1 24.0 * 36.4 74.3 * 417.1 8.8 8.7 17.2 15.8 29.6 113.7 50 4.2 5.40 5.4 33.7 83.5 162.0 3.2 3.7 3.8 8.4 20.6 36.1 100 2.2 2.90 3.0 32.8 81.4 159.0 1.8 2.2 2.3 7.6 19.6 34.1 150 1.5 1.99 2.1 33.0 79.2 158.0 1.3 1.5 1.7 7.3 18.7 33.1 200 1.1 1.50 1.6 29.4 76.4 145.1 1.0 1.2 1.3 7.3 18.3 33.6 300 0.8 1.00 1.0 31.4 84.5 159.3 0.7 0.8 1.0 7.7 18.2 32.6 400 * 0.80 0.9 * 74.0 160.5 0.5 0.7 0.7 7.1 16.8 32.7 500 * 0.60 * * 68.9 * 0.4 0.5 0.6 7.1 16.8 31.2 700 * 0.40 0.5 * 63.5 97.2 0.3 0.4 0.4 6.5 16.1 32.4 1000 * 0.30 * * 67.3 * * 0.3 0.3 * 17.2 34.2 
下载: 导出CSV
表 2 Jund法得到的热导率. *代表温度梯度线性程度十分糟糕; —代表体系崩溃. 1—9代表了在冷区和热区抽取和注入的热流(单位: eV/ps)
Table 2. Thermal conductivity obtained by Jund method. * represents a very poor linearity of temperature gradient; – represents the system collapse. 1–9 represents the heat flow (unit: eV/ps) extracted and injected in cold and hot regions.
模型 长度/nm 热流/(eV·ps–1) 1 2 3 4 5 6 7 8 9 碳纳米管 60 31.40 31.66 * — — — — — — 200 77.07 32.80 * 46.26 * * * * * 500 184.46 181.25 * * * * 270.25 * * 碳化硅纳米管 60 6.90 5.41 6.87 7.98 8.52 — — — — 200 16.96 10.98 * 22.03 23.53 24.21 25.02 — — 500 30.23 33.22 34.19 31.27 35.79 37.89 39.62 44.21 44.21
下载: 导出CSV
-
[1] Ouyang Y L, Zhang Z W, Li D F, Chen J, Zhang G 2019 Ann. Phys. 531 1800437
Google Scholar
[2] Zhang Z, Ouyang Y, Cheng Y, Chen J, Li N, Zhang G 2020 Phys. Rep. 860 1
Google Scholar
[3] Ren W, Ouyang Y, Jiang P, Yu C, He J, Chen J 2021 Nano Lett. 21 2634
Google Scholar
[4] Yang N, Xu X, Zhang G, Li B 2012 AIP Adv. 2 041410
Google Scholar
[5] Zhang R, Lee S, Law C K, Li W K, Teo B K 2002 Chem. Phys. Lett. 364 251
Google Scholar
[6] Durgun E, Tongay S, Ciraci S 2005 Phys. Rev. B 72 075420
Google Scholar
[7] He T, Zhao M, Li W, Lin X, Zhang X, Liu X, Xia Y, Mei L 2008 Nanotechnology 19 205707
Google Scholar
[8] Menon M, Richter E, Mavrandonakis A, Froudakis G, Andriotis A N 2004 Phys. Rev. B 69 115322
Google Scholar
[9] Balandin A A 2011 Nat. Mater. 10 569
Google Scholar
[10] Berber S, Kwon Y K, Tomanek D 2000 Phys. Rev. Lett. 84 4613
Google Scholar
[11] Padgett C W, Brenner D W 2004 Nano Lett. 4 1051
Google Scholar
[12] Donadio D, Galli G 2007 Phys. Rev. Lett. 99 255502
Google Scholar
[13] Moreland J F 2004 Microscale Thermophys. Eng. 8 61
Google Scholar
[14] Lukes J R, Zhong H 2007 J. Heat Transfer 129 705
Google Scholar
[15] Zhang G, Li B 2005 J. Chem. Phys. 123 114714
Google Scholar
[16] Maruyama S 2002 Phys. B 323 193
Google Scholar
[17] Mingo N, Broido D A 2005 Nano Lett. 5 1221
Google Scholar
[18] Shiomi J, Maruyama S 2007 Thermal Engineering Summer Heat Transfer Conference Vancouver, British Columbia, Canada, July 8–12, 2007 p381
[19] Wang J, Wang J S 2006 Appl. Phys. Lett. 88 111909
Google Scholar
[20] Yao Z, Wang J S, Li B, Liu G R 2005 Phys. Rev. B 71 085417
Google Scholar
[21] 保文星, 朱长纯 2006 55 3552
Google Scholar
Bao W X, Zhu C C 2006 Acta Phys. Sin. 55 3552
Google Scholar
[22] 侯泉文, 曹炳阳, 过增元 2009 58 7809
Google Scholar
Hou Q W, Cao B Y, Guo Z Y 2009 Acta Phys. Sin. 58 7809
Google Scholar
[23] 王照亮, 梁金国, 唐大伟 2008 57 3391
Google Scholar
Wang Z L, Liang J G, Tang D W 2008 Acta Phys. Sin. 57 3391
Google Scholar
[24] Osman M A, Srivastava D 2001 Nanotechnology 12 21
Google Scholar
[25] Cao J X, Yan X H, Xiao Y, Ding J W 2004 Phys. Rev. B 69 073407
Google Scholar
[26] Maruyama S 2003 Microscale Thermophys. Eng. 7 41
Google Scholar
[27] Che J, Cagin T, Goddard III W A 2000 Nanotechnology 11 65
Google Scholar
[28] Bai D 2011 Fullerenes, Nanotubes, Carbon Nanostruct 19 271
Google Scholar
[29] Lyver J W, Blaisten-Barojas E 2011 J. Comput. Theor. Nanosci. 8 529
Google Scholar
[30] Shen H 2009 Comput. Mater. Sci. 47 220
Google Scholar
[31] Mingo N, Broido D A 2005 Phys. Rev. Lett. 95 096105
Google Scholar
[32] Chen J, Zhang G, Li B W 2010 J. Phys. Soc. Jpn. 79 074604
Google Scholar
[33] Müller-Plathe F 1997 J. Chem. Phys. 106 6082
Google Scholar
[34] Jund P, Jullien R 1999 Phys. Rev. B 59 13707
Google Scholar
[35] Nieto-Draghi C, Avalos J B 2009 Mol. Phys. 101 2303
[36] Zhang M, Lussetti E, de Souza L E, Muller-Plathe F 2005 J. Phys. Chem. B 109 15060
Google Scholar
[37] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[38] Tersoff J 1989 Phys. Rev. B 39 5566
Google Scholar
[39] Schelling P K, Phillpot S R, Keblinski P 2002 Phys. Rev. B 65 144306
Google Scholar
[40] Sellan D P, Landry E S, Turney J E, McGaughey A J H, Amon C H 2010 Phys. Rev. B 81 214305
Google Scholar
[41] Zhang W, Zhu Z, Wang F, Wang T, Sun L, Wang Z 2004 Nanotechnology 15 936
Google Scholar
下载:
计量
- 文章访问数: 6185
- PDF下载量: 129
- 被引次数: 0
