-
具备弱剪切或负磁剪切和内部输运势垒的托卡马克运行方式被认为是提高聚变性能的最有前途的方法. 中空电流密度剖面与反磁剪切位形是改进堆芯约束和形成内部输运垒的关键条件之一. 在中国环流器2号A(HL-2A)弹丸注入实验中, 成功地实现了维持时间约为100 ms的中空电流放电. 伴随着中空电流剖面的形成, 同时形成了反磁剪切位形. 由于欧姆加热功率不太高, 且没有外部辅助加热, 只能在稳定的中空电流放电阶段看到内部输运垒形成的趋势. 在弹丸注入后, 电子热扩散系数显著降低, 说明弹丸深度注入改善了能量约束. 等离子体性能的增强: 一方面是由于弹丸注入造成中心高度峰化的电子密度剖面; 另一方面是由于等离子体中心存在负磁剪切. 同时, 中空电流位形有利于改善高密度等离子体的稳定性. 结果还表明, 在中空电流放电中, 等离子体比压值是低的. 为了提高
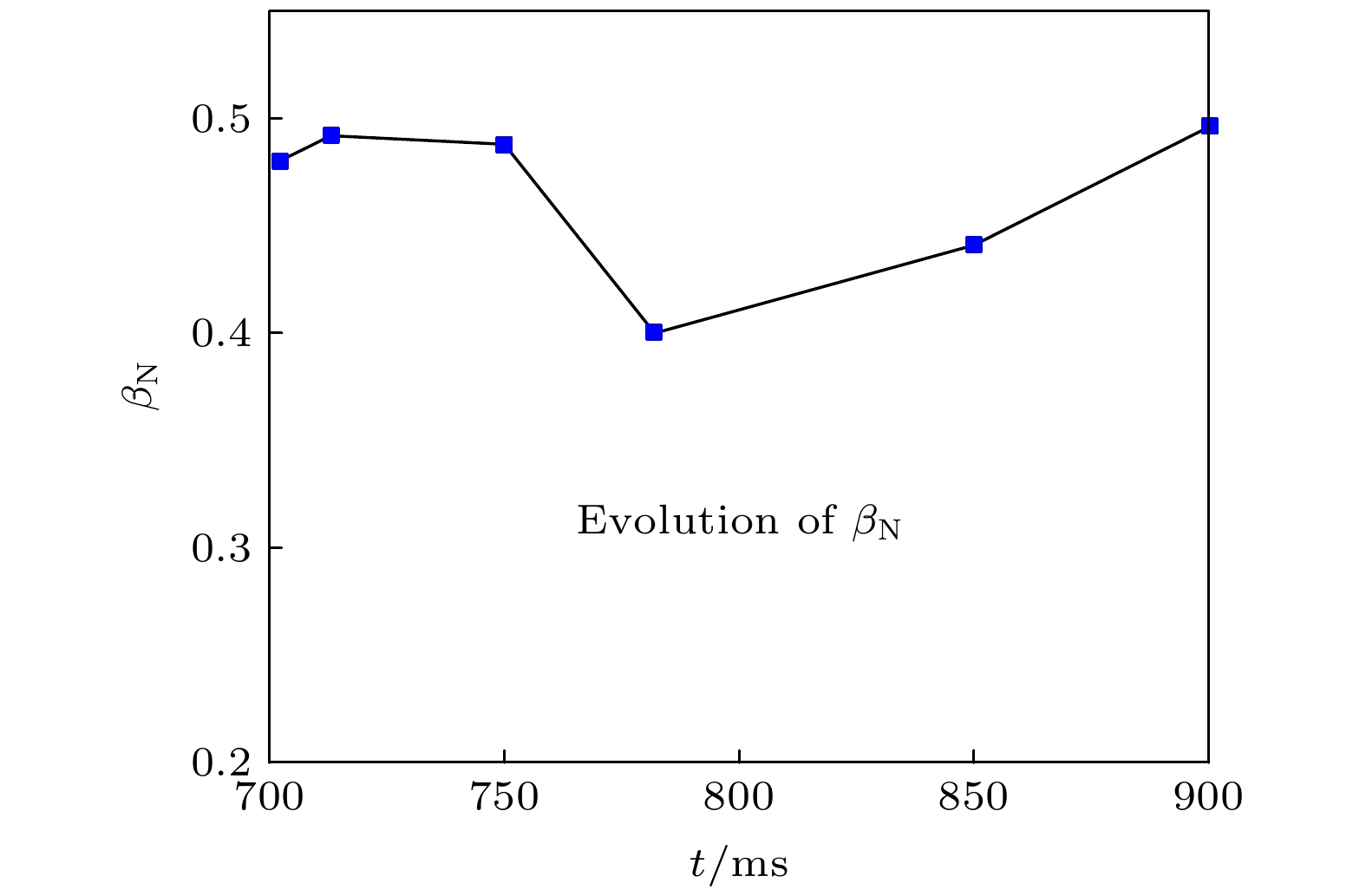
$ {\beta }_{N} $ 极限, 可在等离子体边界附近放置导电壁. HL-2A弹丸注入实验的结果, 为在限制器托卡马克上获得高参数放电提供了一种可能.The tokamak with weak or negative magnetic shear and internal transport barrier (ITB) is considered to be the most promising approach to improving fusion performance. The hollow current density profile, as well as the reversed q profile (negative magnetic shear), is one of the key conditions for improving core confinement in advanced tokamak schemes. In the Huanliuqi 2A (HL-2A) experiment, a hollow current distribution with a discharge duration of about 100 ms is successfully achieved by injecting the pellets in the Ohmic discharge. The discharge is characteristic of circular equilibrium configuration and three frozen pellets are injected continuously at three different time moments. As a result, the hollow current profiles are formed in the plasma with weak hollow electron temperature in the core region. At the same time, the hollow currents are combined with the reversed magnetic shear profiles. Because the power of Ohmic heating is not so high and there is no external auxiliary heating, we can see only a trend of the formation of weak internal transport barrier in the stable hollow current discharge stage. However, the electron thermal diffusivity decreases significantly after the pellets have been injected. The deep injection of frozen pellets improves the energy confinement. The enhancement of plasma performance is due to the peaked electron density profile in the center, caused by pellet injection and the negative magnetic shear in the plasma center. It is concluded that the electron density profile peaked highly in the core plasma, caused by pellet injection, is beneficial to the improvement of particle confinement and plays an important role in enhancing the energy confinement. In addition, it is also demonstrated that, in general, during a hollow current discharge, the poloidal beta$ {\beta }_{\mathrm{p}} $ value and normalized beta$ {\beta }_{\mathrm{N}} $ value are both obviously low although the reversed magnetic shear is conducive to stabilizing ballooning modes and weakening the drift instabilities. However, comparing with the hollow current profile, the plasma with peaked current profile is very beneficial to the improvement of beta limit. In order to improve the$ {\beta }_{\mathrm{N}} $ limit, a conductive wall is necessary to be placed near the plasma boundary. The results of HL-2A pellet injection experiments present a possibility of obtaining high parameter discharge on a limiter tokamak.[1] Strait E J, Lao L L, Mauel M E, Rice B W, Taylor T S, Burrell K H, Chu M S, Lazarus E A, Osborne T H, Thompson S J, Turnbull A D, 1995 Phys. Rev. Lett. 75 4421
Google Scholar
[2] Turnbull A D, Taylor T S, Lin-Liu Y R, John H S 1995 Phys. Rev. Lett. 74 718
Google Scholar
[3] Jackson G L, Winter J, Taylor T S, Burrell K H, DeBoo J C, Greenfield C M, Groebner R J, Hodapp T, Holtrop K, Lazarus E A, Lao L L, Lippmann S I, Osborne T H, Petrie T W, Phillips J, James R, Schissel D P, Strait E J, Turnbull A D, West W P 1991 Phys. Rev. Lett. 67 3098
Google Scholar
[4] Levinton F M, Zarnstorff M C, Batha S H, Bell M, Bell R E, Budny R V, Bush C, Chang Z, Fredrickson E, Janos A, Manickam J, Ramsey A, Sabbagh S A, Schmidt G L, Synakowski E J, Taylor G 1995 Phys. Rev. Lett. 75 4417
Google Scholar
[5] Kessel C, Manickam J, Rewoldt G, Tang W M 1994 Phys. Rev. Lett. 72 1212
Google Scholar
[6] Hawkes N C, Stratton B C, Tala T, Challis C D, Conway G, DeAngelis R, Giroud C, Hobirk J, Joffrin E, Lomas P, Lotte P, Mailloux J, Mazon D, Rachlew E, Reyes-Cortes S, Solano E, Zastrow K D 2001 Phys. Rev. Lett. 87 115001
Google Scholar
[7] Yavorskij V, Goloborod’ko V, Schoepf K, Sharapov S E, Challi C D, Reznik S, Stork D 2003 Nucl. Fusion 43 1077
Google Scholar
[8] Zarnstorff M C, Bell M G, Bitter M, Goldston R J, Grek B, Hawryluk R J, Hill K, Johnson D, McCune D, Park H, Ramsey A, Taylor G, Wieland R 1988 Phys. Rev. Lett. 60 1306
Google Scholar
[9] Fujita T, Kamada Y, Ishida S, Neyatani Y, Oikawa T, Ide S, Takeji S, Koide Y, Isayama A, Fukuda T, Hatae T, Ishii Y, Ozeki T, Shirai H, JT-60 Team 1999 Nucl. Fusion 39 1627
Google Scholar
[10] Sengoku S, Nagami M, Abe M, Hoshino K, Kameari A, Kitsunezaki A, Konoshima S, Matoba T, Oikawa A, Shimada M, Suzuki N, Takahashi H, Tani K, Washizu M, Foster C A, Milora S L, Attenberger S E, Stockdale R E 1985 Nucl. Fusion 25 1475
Google Scholar
[11] Yan L W, Xiao Z G, Zheng Y J, Dong J F, Deng Z C, Li B, Li L, Feng Z, Liu Y, Wang E Y 2002 Nucl. Fusion 42 265
Google Scholar
[12] Ding X T, Yang Q W, Yan L W, Zhu G L, Xiao Z G, Liu D Q, Cao Z, Gao Q D, Long Y X, Liu Yi, Zhou Y, Pan Y D, Cui Z Y, Huang Y, Liu Z T, Shi Z B, Ji X Q, Xiao W W, Liu Y 2006 Chin. Phys. Lett. 23 2502
Google Scholar
[13] Valovič M, Garzotti L, Gurl C, Akers R, Harrison J, Michael C, Naylor G, Scannell R 2012 Nucl. Fusion 52 114022
Google Scholar
[14] 刘春华, 聂林, 黄渊, 季小全, 余德良, 刘仪, 冯震, 姚可, 崔正英, 严龙文, 丁玄同, 董家齐, 段旭如 2012 61 205201
Google Scholar
Liu C H, Nie L, Huang Y, Ji X Q, Yu D L, Liu Yi, Feng Z, Yao K, Cui Z Y, Yan L W, Ding X T, Dong J Q, Duan X R 2012 Acta Phys. Sin. 61 205201
Google Scholar
[15] Furth H P 1986 Plasma Phys. Controlled Fusion 28 1305
Google Scholar
[16] Hugon M, Milligen B Ph van, Smeulders P, Appel LC, Bartlett DV, Boucher D, Edwards AW, Eriksson L-G, Gowers C W, Hender T C, Huysmans G, Jacquinot J J, Kupschus P, Porte L, Rebut P H, Start D F H, Tibone F, Tubbing B J D, Watkins M L, Zwingmann W 1992 Nucl. Fusion 32 33
Google Scholar
[17] Nagami M 1989 Plasma Phys. Controlled Fusion 31 1597
Google Scholar
[18] Jayakumar R J, Austin M A, Greenfield C M, Hawkes N C, Kinsey J E, Lao L L, Parks P B, Solano E R, Taylor T S 2008 Nucl. Fusion 48 015004
Google Scholar
[19] Liu Yi, Qiu X M, Dong Y B, Guo G C, Xiao Z G, Zhong Y Z, Zheng Y J, Fu B Z, Dong J F, Liu Yong, Wang E Y 2004 Plasma Phys. Controled Fusion 46 455
Google Scholar
[20] Shen Y, Dong J Q, He H D, Shi Z B, Li J, Han M K, Li J Q, Sun A P, Pan L 2020 Nucl. Fusion 60 124001
Google Scholar
[21] Tala T J J, Parail V V, Becoulet A, Challis C D, Corrigan G, Hawkes N C, Heading D J, Mantsinen M J, Nowak S 2002 Plasma Phys. Controlled Fusion 44 1181
Google Scholar
[22] Litaudon X, Peysson Y, Aniel T, Huysmans G, Imbeaux F, Joffrin E, Lasalle J, Lotte P, Schunke B, Segui J L, Tresset G, Zabiego M 2001 Plasma Phys. Controlled. Fusion 43 677
Google Scholar
[23] Challis C D, Litaudon X, Tresset G, Baranov Yu F, Bécoulet A, Giroud C, Hawkes N C, Howell D F, Joffrin E, Lomas P J, Mailloux J, Mantsinen M J, Stratton B C, Ward D J, Zastrow K D 2002 Plasma Phys. Controlled. Fusion 44 1031
Google Scholar
[24] Fujita T, Oikawa T, Suzuki T, Ide S, Sakamoto Y, Koide Y, Hatae T, Naito O, Isayama A, Hayashi N, Shirai H 2001 Phys. Rev. Lett. 87 245001
Google Scholar
[25] Lao L L, Ferron J R, Groebner R J, Howl W, John H St, Strait E J, Taylor T S 1990 Nucl. Fusion 30 1035
Google Scholar
[26] Lao L L, John H St, Stambaugh R D, Kellman A G, Pfeiffer W 1985 Nucl. Fusion 25 1611
[27] He H D, Dong J Q, Zheng G Y, He Z X, Lu G M, Peng X D, Shi Z B, Zhang J H 2012 Phys. Scr. 85 045501
Google Scholar
[28] Gruber R, Troyon F, Berger D, Bernard L C, Rousset S, Schreiber R, Schneider W, Roberts K V 1981 Comput. Phys. Commun. 21 323
Google Scholar
[29] Smeulders P, Appel L C, Balet B, Hender T C, Lauro-Taroni L, Stork D, Wolle B, Ali-Arshad S, Alper B, Blank H J De, Bures M, Esch B De, Giannella R, Konig R, Kupschus P, Lawson K, Marcus F B, Mattioli M, Morsi H W, O'Brien D P, O'Rourke J, Sadler G J, Schmidt G L, Stubberfield P M, Zwingmann W 1995 Nucl. Fusion 35 225
[30] Dong J Q, Horton W 1995 Phys. Plasmas 2 3412
Google Scholar
[31] 沈勇, 董家齐, 徐红兵 2018 67 195203
Google Scholar
Shen Y, Dong J Q, Xu H B 2018 Acta Phys. Sin. 67 195203
Google Scholar
[32] Rebut P-H, Watkins M L, Gambier D J, Boucheret D 1992 Phys. Fluids B 3 2209
[33] Maget P, Garbet X, Géraud A, Joffrin E 1999 Nucl. Fusion 39 949
Google Scholar
[34] Gao Q D, Budny R V, Zhang J H, Li F Z, Jiao Y M 2000 Nucl. Fusion 40 1897
Google Scholar
[35] 沈勇, 董家齐, 何宏达 2016 真空科学与技术学报 36 447
Shen Y, Dong J Q, He H D 2016 Chin. J. Vac. Sci. Technol. 36 447
[36] Gao Q D, Budny R V, Li F, Zhang J 2003 Nucl. Fusion 43 982
Google Scholar
-
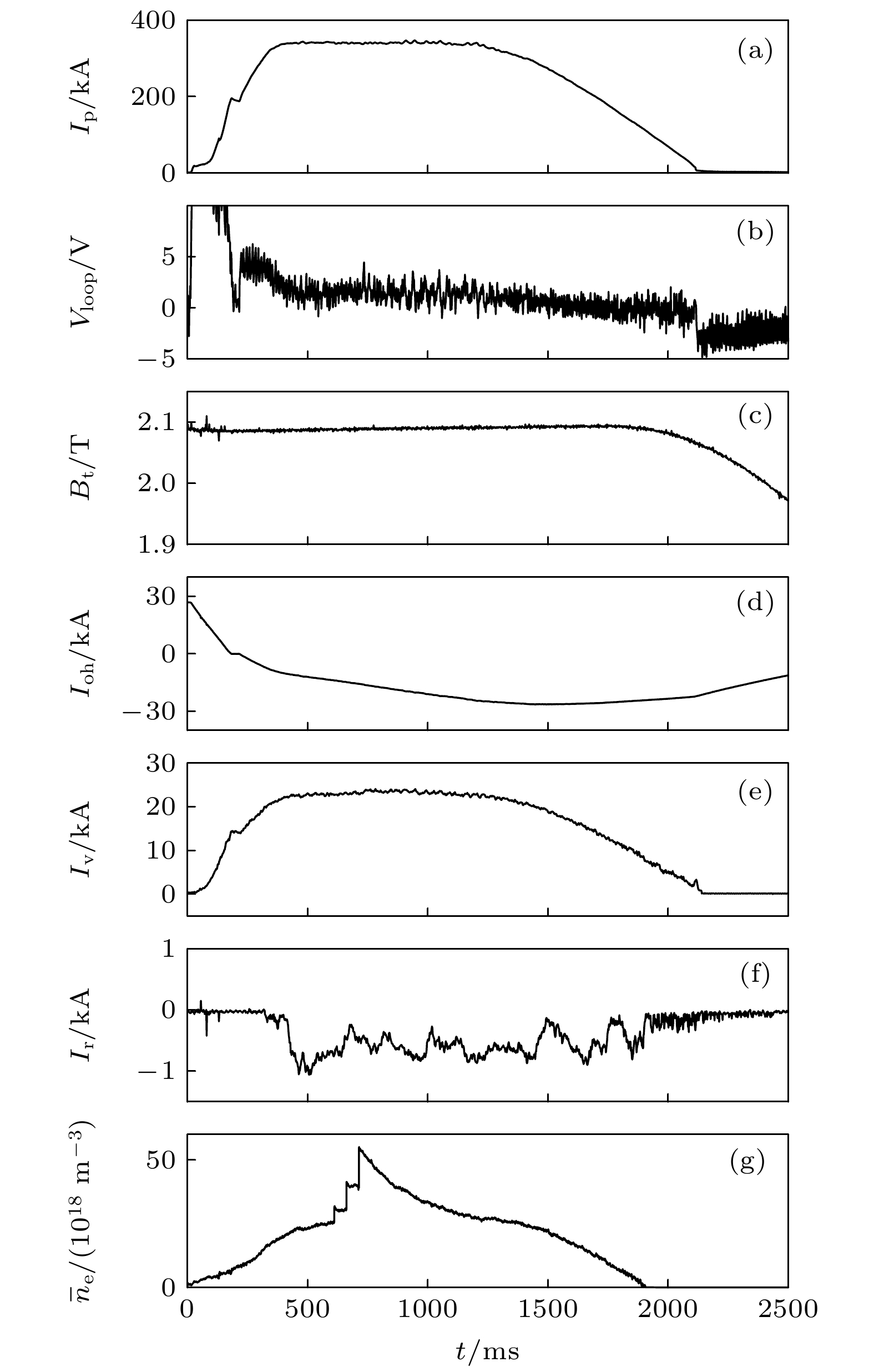
图 1 典型弹丸注入放电(4050炮)参数的时间演化 (a)等离子体电流
$ {I}_{\mathrm{p}} $ ; (b)环电压$ {V}_{\mathrm{l}\mathrm{o}\mathrm{o}\mathrm{p}} $ ; (c)纵向磁场$ {B}_{\mathrm{t}} $ ; (d)欧姆电流$ {I}_{\mathrm{o}\mathrm{h}} $ ; (e) 垂直场线圈电流$ {I}_{\mathrm{v}} $ ; (f) 水平场线圈电流$ {I}_{\mathrm{r}} $ ; (g) 线平均电子密度$ {\bar {n}}_{\mathrm{e}} $ Fig. 1. Temporal evolutions of the typical pellet injection discharge: (a) Plasma current
$ {I}_{\mathrm{p}} $ ; (b) loop voltage$ {V}_{\mathrm{l}\mathrm{o}\mathrm{o}\mathrm{p}} $ ; (c) longitudinal magnetic field$ {B}_{\mathrm{t}} $ ; (d) Ohmic current$ {I}_{\mathrm{o}\mathrm{h}} $ ; (e) vertical field coil current$ {I}_{\mathrm{v}} $ ; (f) horizontal field coil current$ {I}_{\mathrm{r}} $ ; (g) average line electron density$ {\bar {n}}_{\mathrm{e}} $ .
图 2 性能参数图 (a)极向
$ {\beta }_{\mathrm{p}} $ 和能量约束时间$ {\tau }_{\mathrm{E}} $ 的时间演化; (b)离子温度$ {T}_{\mathrm{i}} $ 和热辐射强度$ {I}_{\mathrm{b}\mathrm{o}\mathrm{l}} $ 的时间演化; (c)电子热扩散系数$ {\chi }_{\mathrm{e}} $ 的时间演化, 其中阴影部分表示3次弹丸注入时间段Fig. 2. Performance parameters: (a) The Poloidal
$ {\beta }_{\mathrm{p}} $ and energy confinement time$ {\tau }_{\mathrm{E}} $ ; (b) ion temperature$ {T}_{\mathrm{i}} $ and thermal radiation intensity$ {I}_{\mathrm{b}\mathrm{o}\mathrm{l}} $ ; (c) electron thermal diffusivity$ {\chi }_{\mathrm{e}} $ , where the shaded area represents the time period of the three pellet injections.
图 3 不同通道的软X射线强度图, 从上到下曲线对应的
$ r=2.5 $ ,$ 7.3 $ , 12 和$ 16.3 $ cmFig. 3. Soft X-ray intensity diagram of different channels, where the curves from top to bottom correspond to
$ r=2.5\;, $ $ 7.3\;, $ 12 and 6.3 cm.
图 5 电子密度(a) 与电子温度(b) 的空间分布图
Fig. 5. Spatial distribution of electron density (a) and electron temperature (b).
图 6
$ t=702, \;713, \;782, \;902 $ ms时的(a)电子温度剖面、(b)电子密度剖面和(c)电流剖面Fig. 6. Electron temperature (a), electron density (b) and current (c) profiles at
$ t=\mathrm{702, 713}, \;782 $ and$ 902 $ ms.
图 7
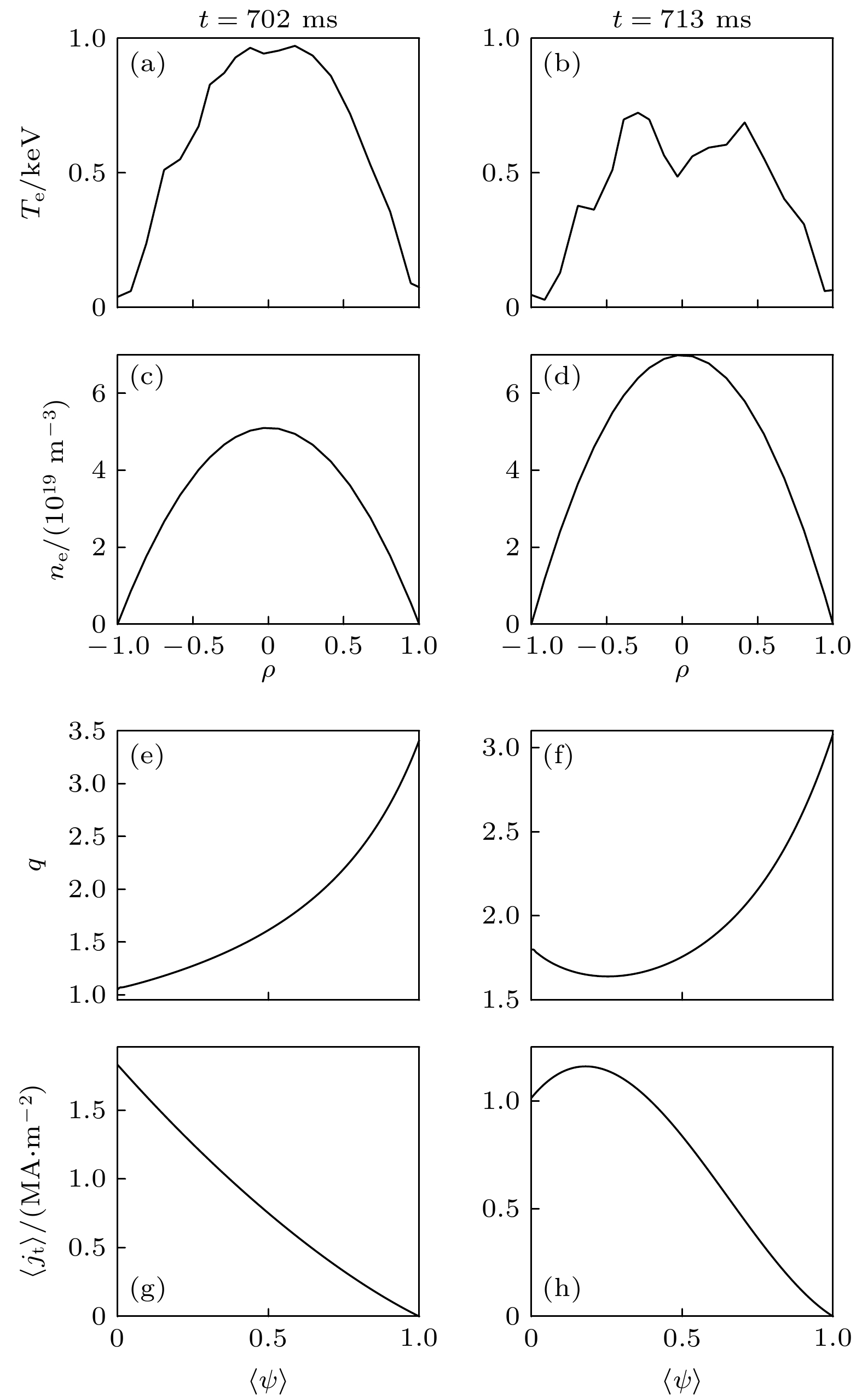
$ t=702 $ 和$ 713 $ ms时的动理学剖面图 (a), (b) 电子温度; (c), (d) 电子密度; (e), (f) q剖面; (g), (h) 平均电流密度$ \left\langle{{j}_{t}}\right\rangle $ Fig. 7. Kinetic profiles at t = 702 and 713 ms: (a), (b) Electron temperature; (c), (d) electron density; (e), (f) q profiles; (g), (h) average current density
$ \left\langle{{j}_{t}}\right\rangle $ profile.
图 8
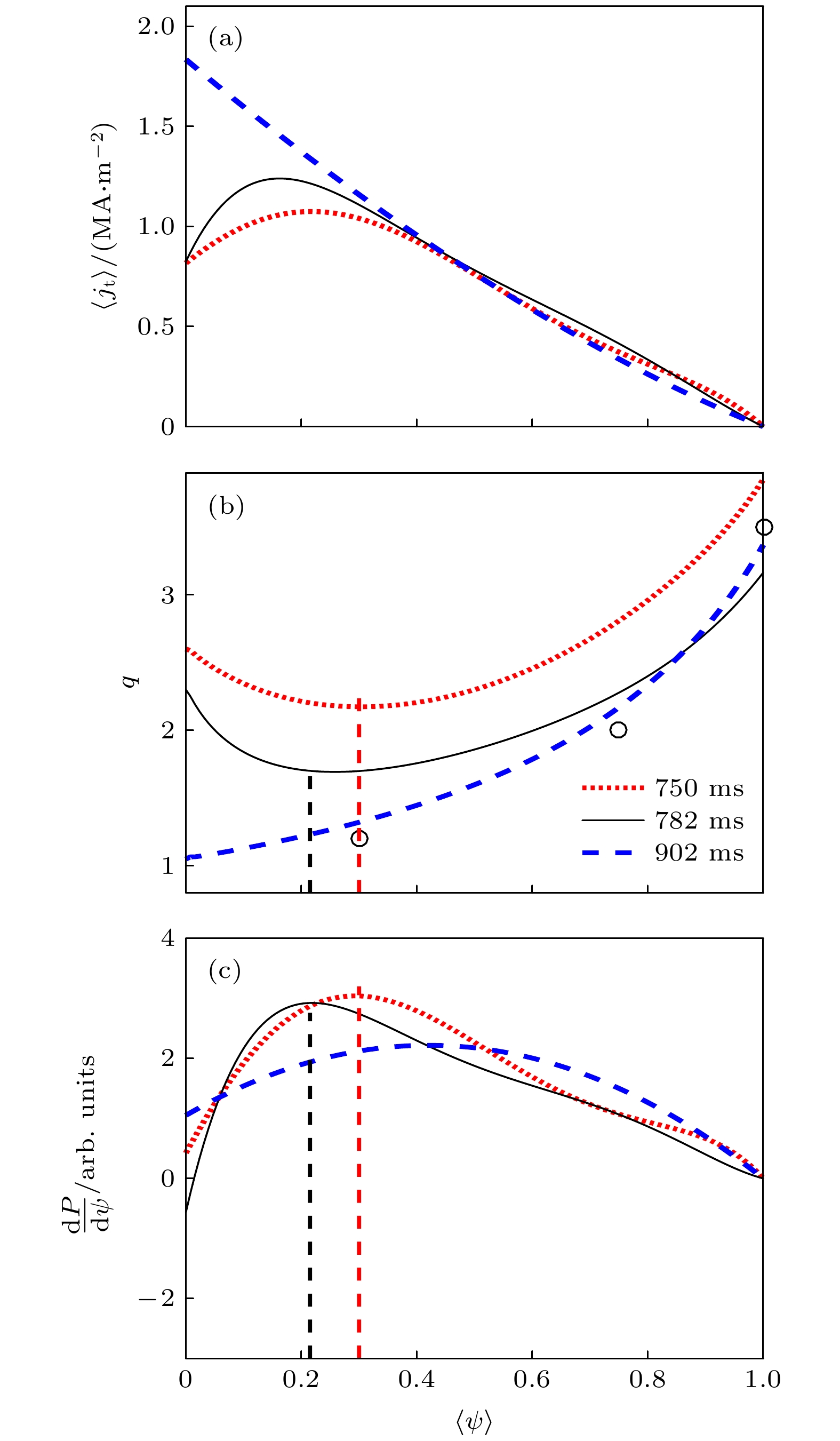
$ t=750, 782, 902 $ ms 时, (a) 电流密度$ \left\langle{{j}_{t}}\right\rangle $ 、(b) 安全因子q、(c)压强梯度$ \mathrm{d}P/\mathrm{d}\psi $ 剖面图. (b)中的“o”表示$ 900 $ ms时刻q测量值, 与重建的q剖面相应点基本重合Fig. 8. : (a) Current density
$ \left\langle{{j}_{\mathrm{t}}}\right\rangle $ , (b) safety factor q, (c) pressure gradient$ \mathrm{d}P/\mathrm{d}\psi $ at$ t=710, \;782 $ and$ 902 $ ms. And the symbols “o” in panel (b) represent the measured q values.
图 9
$ t=782\;\mathrm{m}\mathrm{s}, {q}_{0}=3.2 $ 时, (a)不同$ {\beta }_{\mathrm{p}} $ 平衡位形的q剖面、(b)归一化增长率.Fig. 9. (a) Different q profiles and (b) normalized growth rates for different
$ {\beta }_{\mathrm{p}} $ at$ t=782\;\mathrm{m}\mathrm{s} $ and$ {q}_{0}=3.2 $ .
图 10 EFIT重建的稳定平衡的深反转q剖面及平均电流密度
$ \left\langle{{j}_{t}}\right\rangle $ 分布Fig. 10. Stable equilibrium deeply inverted q profile and average current density
$ \left\langle{{j}_{t}}\right\rangle $ for the stable equilibrium reconstructed by EFIT.
图 11
$ {\beta }_{\mathrm{N}} $ 随时间演化图Fig. 11. Temporal evolution of
$ {\beta }_{\mathrm{N}} $ . -
[1] Strait E J, Lao L L, Mauel M E, Rice B W, Taylor T S, Burrell K H, Chu M S, Lazarus E A, Osborne T H, Thompson S J, Turnbull A D, 1995 Phys. Rev. Lett. 75 4421
Google Scholar
[2] Turnbull A D, Taylor T S, Lin-Liu Y R, John H S 1995 Phys. Rev. Lett. 74 718
Google Scholar
[3] Jackson G L, Winter J, Taylor T S, Burrell K H, DeBoo J C, Greenfield C M, Groebner R J, Hodapp T, Holtrop K, Lazarus E A, Lao L L, Lippmann S I, Osborne T H, Petrie T W, Phillips J, James R, Schissel D P, Strait E J, Turnbull A D, West W P 1991 Phys. Rev. Lett. 67 3098
Google Scholar
[4] Levinton F M, Zarnstorff M C, Batha S H, Bell M, Bell R E, Budny R V, Bush C, Chang Z, Fredrickson E, Janos A, Manickam J, Ramsey A, Sabbagh S A, Schmidt G L, Synakowski E J, Taylor G 1995 Phys. Rev. Lett. 75 4417
Google Scholar
[5] Kessel C, Manickam J, Rewoldt G, Tang W M 1994 Phys. Rev. Lett. 72 1212
Google Scholar
[6] Hawkes N C, Stratton B C, Tala T, Challis C D, Conway G, DeAngelis R, Giroud C, Hobirk J, Joffrin E, Lomas P, Lotte P, Mailloux J, Mazon D, Rachlew E, Reyes-Cortes S, Solano E, Zastrow K D 2001 Phys. Rev. Lett. 87 115001
Google Scholar
[7] Yavorskij V, Goloborod’ko V, Schoepf K, Sharapov S E, Challi C D, Reznik S, Stork D 2003 Nucl. Fusion 43 1077
Google Scholar
[8] Zarnstorff M C, Bell M G, Bitter M, Goldston R J, Grek B, Hawryluk R J, Hill K, Johnson D, McCune D, Park H, Ramsey A, Taylor G, Wieland R 1988 Phys. Rev. Lett. 60 1306
Google Scholar
[9] Fujita T, Kamada Y, Ishida S, Neyatani Y, Oikawa T, Ide S, Takeji S, Koide Y, Isayama A, Fukuda T, Hatae T, Ishii Y, Ozeki T, Shirai H, JT-60 Team 1999 Nucl. Fusion 39 1627
Google Scholar
[10] Sengoku S, Nagami M, Abe M, Hoshino K, Kameari A, Kitsunezaki A, Konoshima S, Matoba T, Oikawa A, Shimada M, Suzuki N, Takahashi H, Tani K, Washizu M, Foster C A, Milora S L, Attenberger S E, Stockdale R E 1985 Nucl. Fusion 25 1475
Google Scholar
[11] Yan L W, Xiao Z G, Zheng Y J, Dong J F, Deng Z C, Li B, Li L, Feng Z, Liu Y, Wang E Y 2002 Nucl. Fusion 42 265
Google Scholar
[12] Ding X T, Yang Q W, Yan L W, Zhu G L, Xiao Z G, Liu D Q, Cao Z, Gao Q D, Long Y X, Liu Yi, Zhou Y, Pan Y D, Cui Z Y, Huang Y, Liu Z T, Shi Z B, Ji X Q, Xiao W W, Liu Y 2006 Chin. Phys. Lett. 23 2502
Google Scholar
[13] Valovič M, Garzotti L, Gurl C, Akers R, Harrison J, Michael C, Naylor G, Scannell R 2012 Nucl. Fusion 52 114022
Google Scholar
[14] 刘春华, 聂林, 黄渊, 季小全, 余德良, 刘仪, 冯震, 姚可, 崔正英, 严龙文, 丁玄同, 董家齐, 段旭如 2012 61 205201
Google Scholar
Liu C H, Nie L, Huang Y, Ji X Q, Yu D L, Liu Yi, Feng Z, Yao K, Cui Z Y, Yan L W, Ding X T, Dong J Q, Duan X R 2012 Acta Phys. Sin. 61 205201
Google Scholar
[15] Furth H P 1986 Plasma Phys. Controlled Fusion 28 1305
Google Scholar
[16] Hugon M, Milligen B Ph van, Smeulders P, Appel LC, Bartlett DV, Boucher D, Edwards AW, Eriksson L-G, Gowers C W, Hender T C, Huysmans G, Jacquinot J J, Kupschus P, Porte L, Rebut P H, Start D F H, Tibone F, Tubbing B J D, Watkins M L, Zwingmann W 1992 Nucl. Fusion 32 33
Google Scholar
[17] Nagami M 1989 Plasma Phys. Controlled Fusion 31 1597
Google Scholar
[18] Jayakumar R J, Austin M A, Greenfield C M, Hawkes N C, Kinsey J E, Lao L L, Parks P B, Solano E R, Taylor T S 2008 Nucl. Fusion 48 015004
Google Scholar
[19] Liu Yi, Qiu X M, Dong Y B, Guo G C, Xiao Z G, Zhong Y Z, Zheng Y J, Fu B Z, Dong J F, Liu Yong, Wang E Y 2004 Plasma Phys. Controled Fusion 46 455
Google Scholar
[20] Shen Y, Dong J Q, He H D, Shi Z B, Li J, Han M K, Li J Q, Sun A P, Pan L 2020 Nucl. Fusion 60 124001
Google Scholar
[21] Tala T J J, Parail V V, Becoulet A, Challis C D, Corrigan G, Hawkes N C, Heading D J, Mantsinen M J, Nowak S 2002 Plasma Phys. Controlled Fusion 44 1181
Google Scholar
[22] Litaudon X, Peysson Y, Aniel T, Huysmans G, Imbeaux F, Joffrin E, Lasalle J, Lotte P, Schunke B, Segui J L, Tresset G, Zabiego M 2001 Plasma Phys. Controlled. Fusion 43 677
Google Scholar
[23] Challis C D, Litaudon X, Tresset G, Baranov Yu F, Bécoulet A, Giroud C, Hawkes N C, Howell D F, Joffrin E, Lomas P J, Mailloux J, Mantsinen M J, Stratton B C, Ward D J, Zastrow K D 2002 Plasma Phys. Controlled. Fusion 44 1031
Google Scholar
[24] Fujita T, Oikawa T, Suzuki T, Ide S, Sakamoto Y, Koide Y, Hatae T, Naito O, Isayama A, Hayashi N, Shirai H 2001 Phys. Rev. Lett. 87 245001
Google Scholar
[25] Lao L L, Ferron J R, Groebner R J, Howl W, John H St, Strait E J, Taylor T S 1990 Nucl. Fusion 30 1035
Google Scholar
[26] Lao L L, John H St, Stambaugh R D, Kellman A G, Pfeiffer W 1985 Nucl. Fusion 25 1611
[27] He H D, Dong J Q, Zheng G Y, He Z X, Lu G M, Peng X D, Shi Z B, Zhang J H 2012 Phys. Scr. 85 045501
Google Scholar
[28] Gruber R, Troyon F, Berger D, Bernard L C, Rousset S, Schreiber R, Schneider W, Roberts K V 1981 Comput. Phys. Commun. 21 323
Google Scholar
[29] Smeulders P, Appel L C, Balet B, Hender T C, Lauro-Taroni L, Stork D, Wolle B, Ali-Arshad S, Alper B, Blank H J De, Bures M, Esch B De, Giannella R, Konig R, Kupschus P, Lawson K, Marcus F B, Mattioli M, Morsi H W, O'Brien D P, O'Rourke J, Sadler G J, Schmidt G L, Stubberfield P M, Zwingmann W 1995 Nucl. Fusion 35 225
[30] Dong J Q, Horton W 1995 Phys. Plasmas 2 3412
Google Scholar
[31] 沈勇, 董家齐, 徐红兵 2018 67 195203
Google Scholar
Shen Y, Dong J Q, Xu H B 2018 Acta Phys. Sin. 67 195203
Google Scholar
[32] Rebut P-H, Watkins M L, Gambier D J, Boucheret D 1992 Phys. Fluids B 3 2209
[33] Maget P, Garbet X, Géraud A, Joffrin E 1999 Nucl. Fusion 39 949
Google Scholar
[34] Gao Q D, Budny R V, Zhang J H, Li F Z, Jiao Y M 2000 Nucl. Fusion 40 1897
Google Scholar
[35] 沈勇, 董家齐, 何宏达 2016 真空科学与技术学报 36 447
Shen Y, Dong J Q, He H D 2016 Chin. J. Vac. Sci. Technol. 36 447
[36] Gao Q D, Budny R V, Li F, Zhang J 2003 Nucl. Fusion 43 982
Google Scholar
-
[1] 何宇, 陈伟斌, 洪宾, 黄文涛, 张昆, 陈磊, 冯学强, 李博, 刘菓, 孙笑寒, 赵萌, 张悦. 热效应在电流驱动反铁磁/铁磁交换偏置场翻转中的显著作用. , 2024, 73(2): 027501. doi: 10.7498/aps.73.20231374 [2] 马瑞瑞, 陈骝, 仇志勇. 反磁剪切托卡马克等离子体中低频剪切阿尔芬波的理论研究. , 2023, 72(21): 215207. doi: 10.7498/aps.72.20230255 [3] 徐明, 徐立清, 赵海林, 李颖颖, 钟国强, 郝保龙, 马瑞瑞, 陈伟, 刘海庆, 徐国盛, 胡建生, 万宝年, EAST团队. EAST反磁剪切qmin $\approx $ 2条件下磁流体力学不稳定性及内部输运垒物理实验结果简述. , 2023, 72(21): 215204. doi: 10.7498/aps.72.20230721[4] 徐峰, 于国浩, 邓旭光, 李军帅, 张丽, 宋亮, 范亚明, 张宝顺. Pt/Au/n-InGaN肖特基接触的电流输运机理. , 2018, 67(21): 217802. doi: 10.7498/aps.67.20181191 [5] 郑殊, 张甲鹏, 段萍, 魏来, 王先驱. 黏滞等离子体中双撕裂模不稳定性的数值模拟研究. , 2013, 62(2): 025205. doi: 10.7498/aps.62.025205 [6] 於黄忠. 空间电荷限制电流法测量共混体系中空穴的迁移率. , 2012, 61(8): 087204. doi: 10.7498/aps.61.087204 [7] 高矿红, 魏来明, 俞国林, 杨睿, 林铁, 魏彦锋, 杨建荣, 孙雷, 戴宁, 褚君浩. HgCdTe反型层的磁输运性质. , 2012, 61(2): 027301. doi: 10.7498/aps.61.027301 [8] 刘春华, 聂林, 黄渊, 季小全, 余德良, 刘仪, 冯震, 姚可, 崔正英, 严龙文, 丁玄同, 董家齐, 段旭如. HL-2A托卡马克上的边缘局域模特性初步研究. , 2012, 61(20): 205201. doi: 10.7498/aps.61.205201 [9] 杜坚, 王素新, 袁爱国. δ势垒对多臂量子环中持续电流的影响. , 2010, 59(4): 2767-2774. doi: 10.7498/aps.59.2767 [10] 修明霞, 任俊峰, 王玉梅, 原晓波, 胡贵超. 肖特基势垒对铁磁/有机半导体结构自旋注入性质的影响. , 2010, 59(12): 8856-8861. doi: 10.7498/aps.59.8856 [11] 杜坚, 王素新, 杨淑敏. 含双δ势垒三臂量子环的透射概率和持续电流. , 2009, 58(11): 7926-7933. doi: 10.7498/aps.58.7926 [12] 杨 浩, 郭 霞, 关宝璐, 王同喜, 沈光地. 注入电流对垂直腔面发射激光器横模特性的影响. , 2008, 57(5): 2959-2965. doi: 10.7498/aps.57.2959 [13] 杜 坚, 张 鹏, 刘继红, 李金亮, 李玉现. 含δ势垒的铁磁/半导体/铁磁异质结中的自旋输运和渡越时间. , 2008, 57(11): 7221-7227. doi: 10.7498/aps.57.7221 [14] 唐振坤, 王玲玲, 唐黎明, 游开明, 邹炳锁. 磁台阶势垒结构中二维电子气的自旋极化输运. , 2008, 57(9): 5899-5905. doi: 10.7498/aps.57.5899 [15] 颜森林. 注入半导体激光器混沌调制性能与内部相位键控编码方法研究. , 2006, 55(12): 6267-6274. doi: 10.7498/aps.55.6267 [16] 王 浩, 郭 永, 顾秉林. 恒定电场下双磁垒结构中的电子输运行为. , 1999, 48(9): 1723-1732. doi: 10.7498/aps.48.1723 [17] 吴承伟, 郭杏林. 直流电场中电流变体单链的电学行为及剪切强度. , 1997, 46(8): 1500-1507. doi: 10.7498/aps.46.1500 [18] 傅新宇, 董家齐, 应纯同, 刘广均. 平行速度剪切驱动湍流引起的粒子输运. , 1997, 46(3): 474-480. doi: 10.7498/aps.46.474 [19] 王作维, 林志方, 陶瑞宝. 电场方向对电流变液剪切应力的影响. , 1996, 45(4): 640-646. doi: 10.7498/aps.45.640 [20] 陶悦群, 邱励俭. 弹丸消融过程的数值分析(Ⅰ). , 1988, 37(10): 1672-1677. doi: 10.7498/aps.37.1672
下载:
计量
- 文章访问数: 4245
- PDF下载量: 70
- 被引次数: 0
