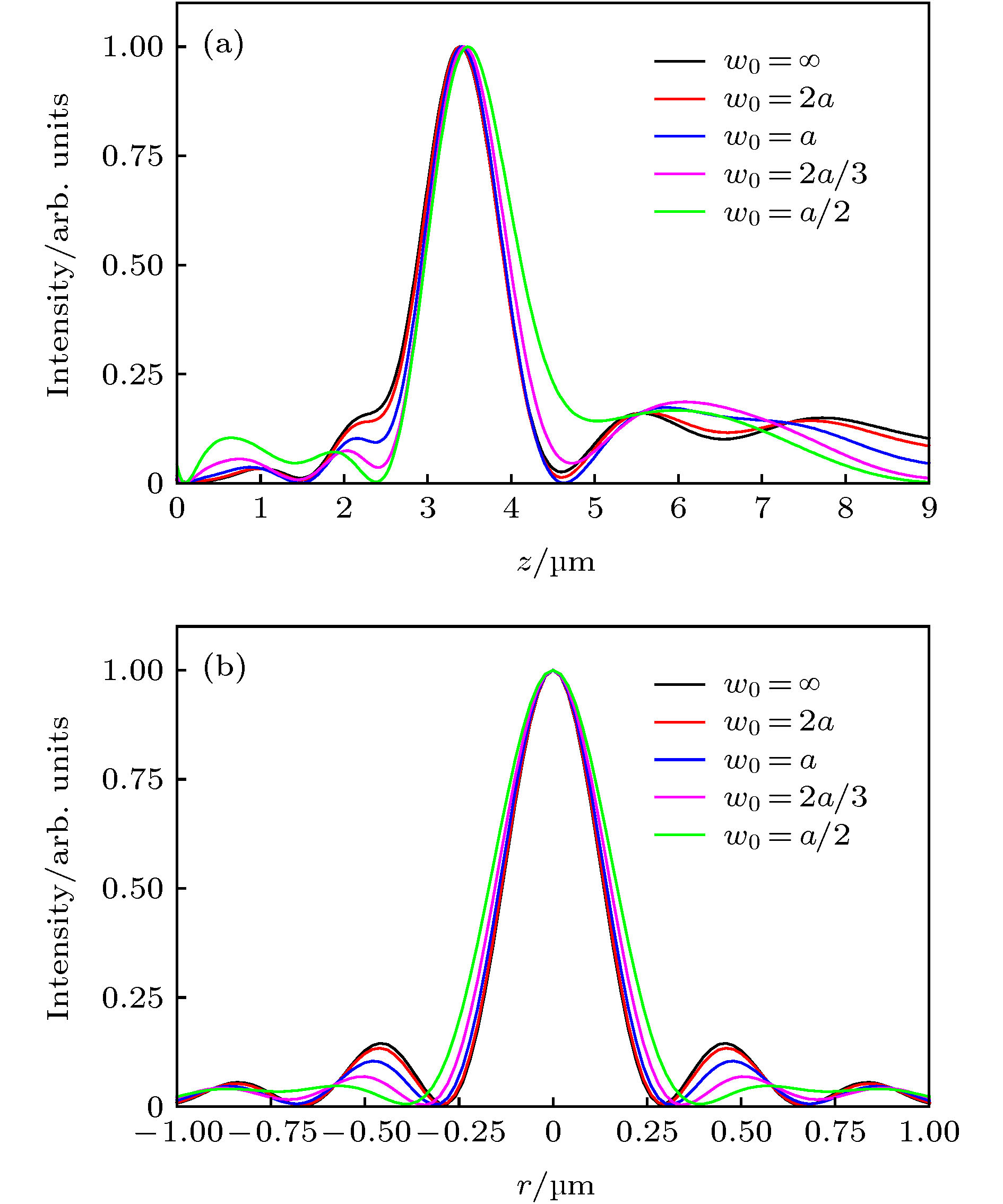
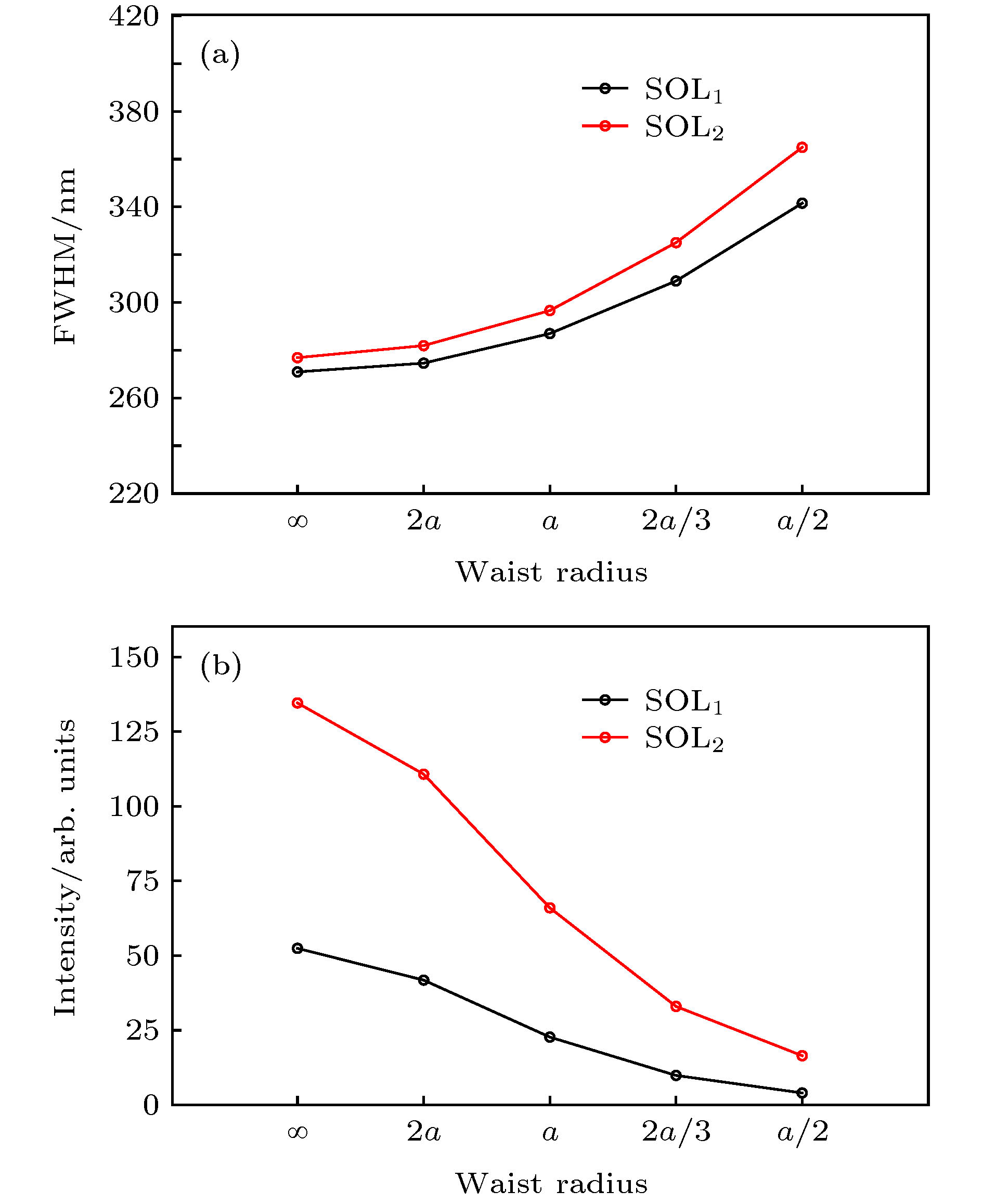
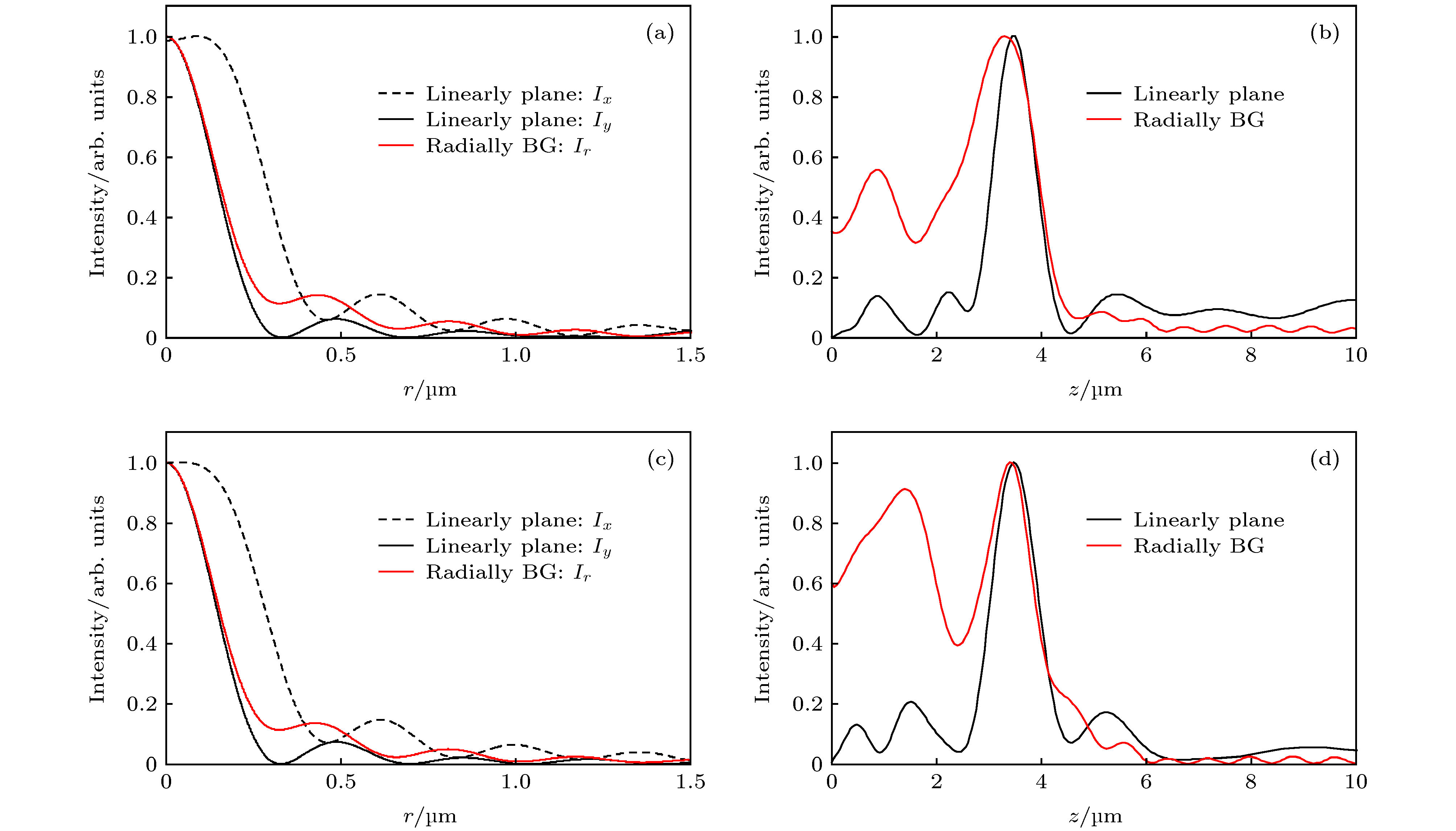
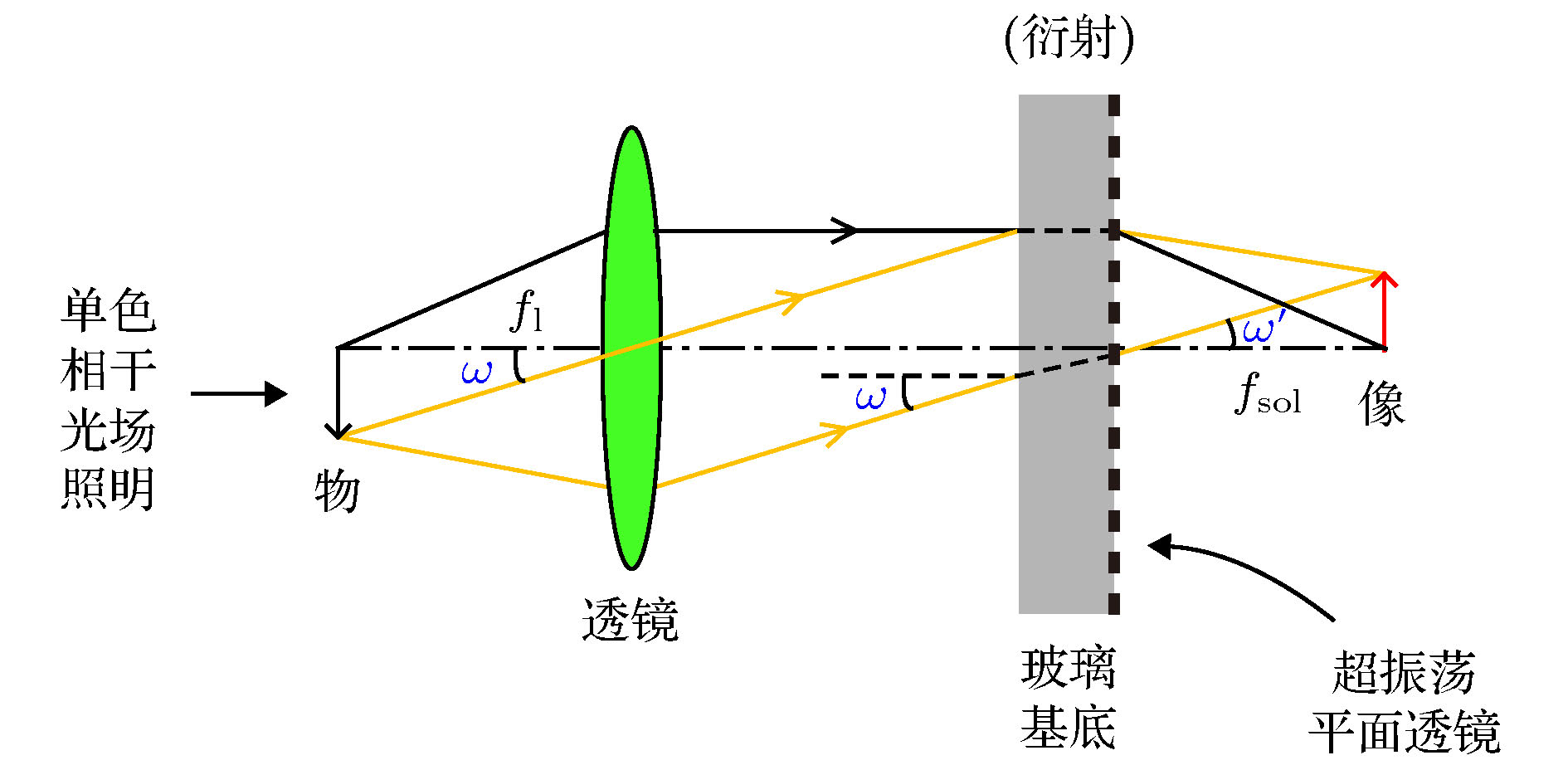
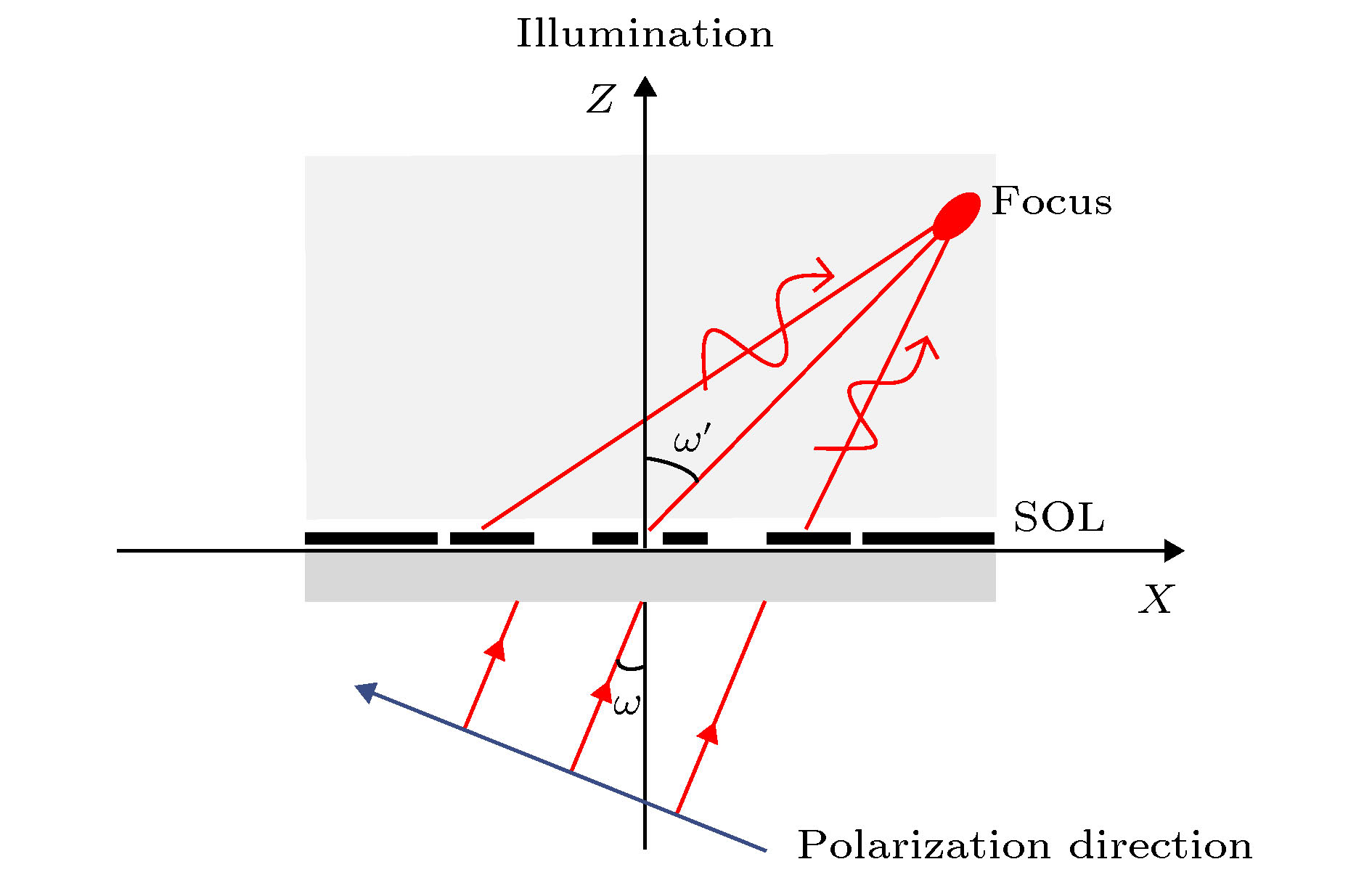
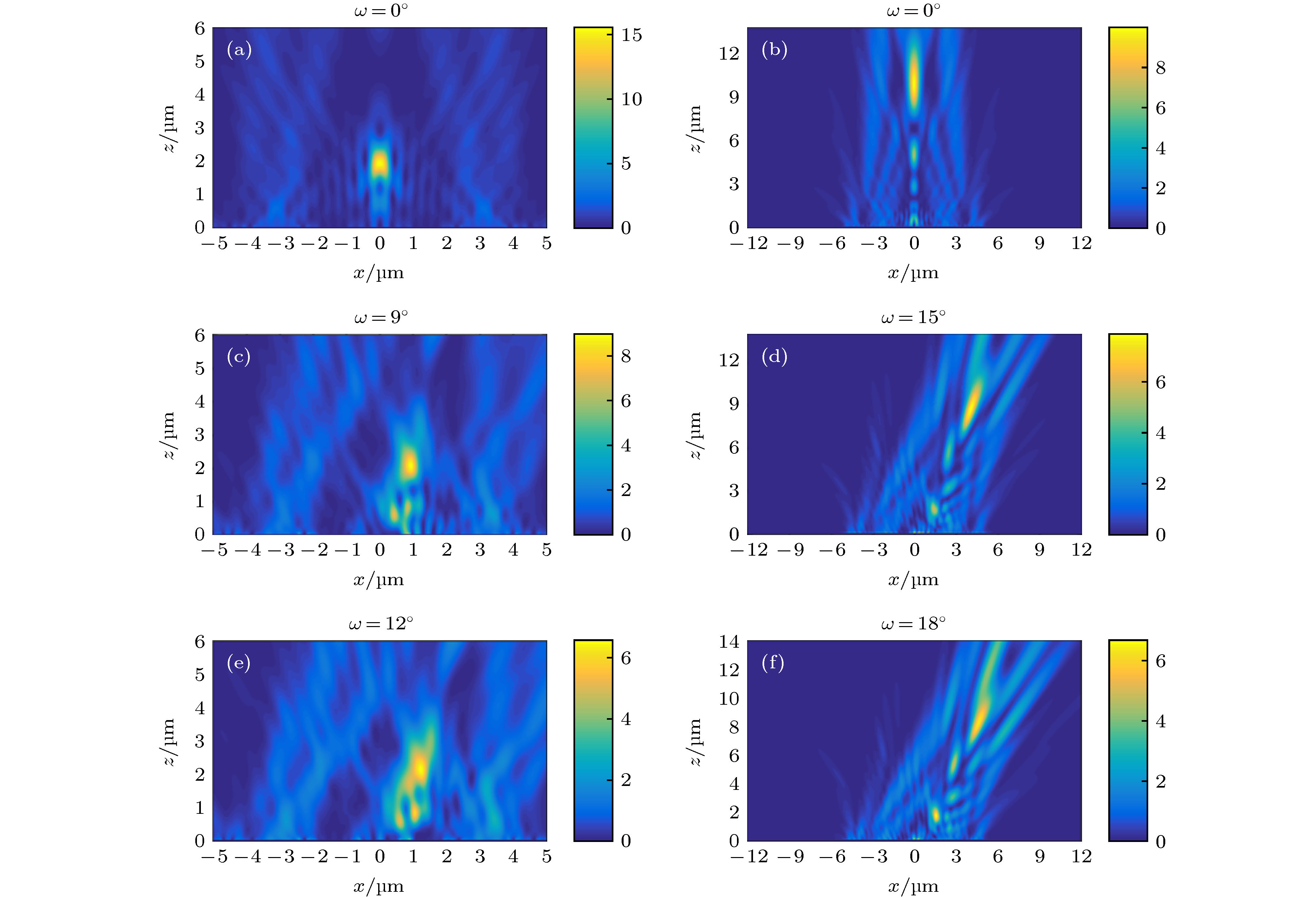
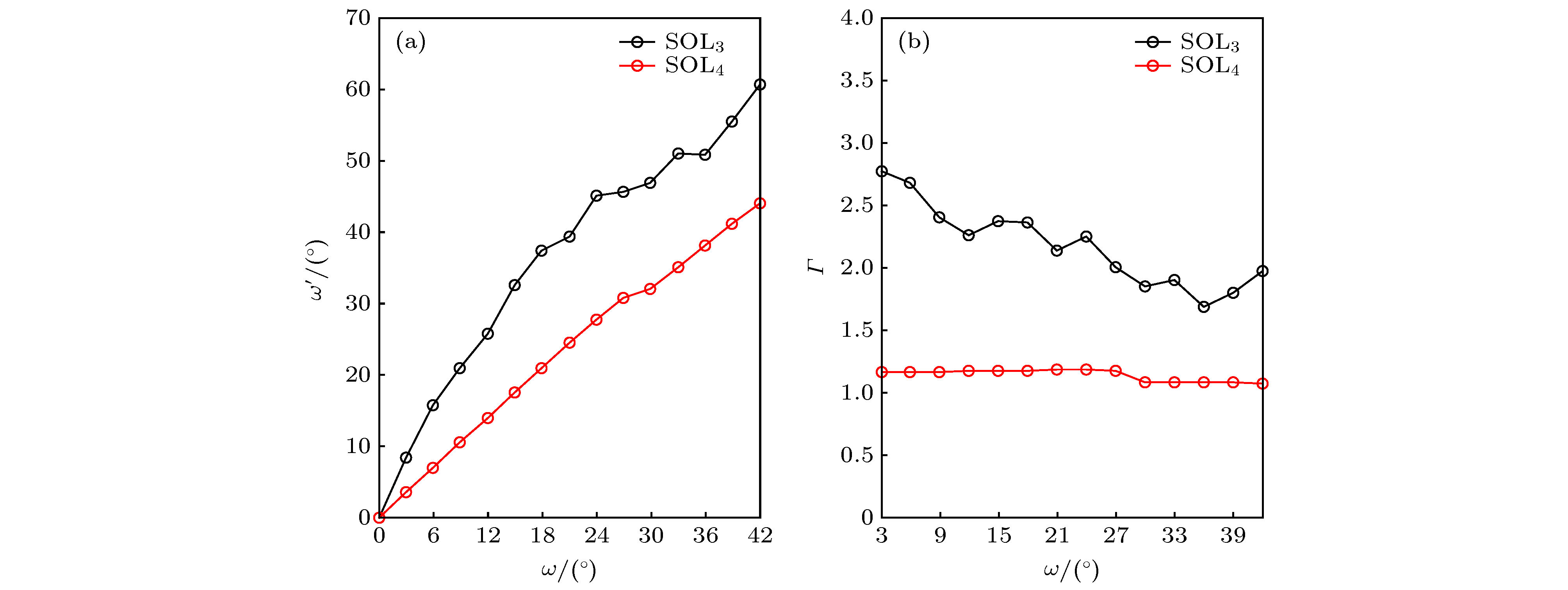
-
超振荡平面透镜(super-oscillatory lens, SOL)是近几年出现的新型平面光学元件, 基于矢量角谱理论设计了振幅型和相位型SOL, 采用时域有限差分法对衍射聚焦光场进行严格电磁仿真计算, 研究发现: 当照明激光束腰半径w0小于SOL半径a时, 超衍射极限聚焦能力明显下降, 聚焦光斑强度衰减超过50%; 束腰半径w0对相位型SOL影响更剧烈, 且会发生显著正向焦移; 当w0不小于2a时可获得接近理想的聚焦特性. 倾斜照明条件下, 大数值孔径振幅型SOL一般允许的倾斜角度小于10°, 而相位型SOL具有宽广的倾角适应性(可超过40°), 聚焦光斑会发生横向展宽, 且强度急剧下降. 大数值孔径SOL对无限远点物成像会产生显著的负畸变和波动变化的场曲, 小数值孔径SOL在宽视场范围内则无畸变. 本文研究结果为SOL在超衍射极限聚焦、超分辨显微成像、飞秒激光直写微纳加工等领域的实际应用提供重要理论支撑.Super-oscillatory lens (SOL), a new type of planar optical element developed in recent years, may play an important role in the integrated optics, microscopy, advanced sensor, and astronomy. Based on the vectorial angular spectrum theory and genetic algorithm, both binary amplitude-type and phase-type SOLs are designed. Various sub-diffraction focusing properties can be realized by optimizing the design procedure. In order to investigate the focusing characteristics of SOLs under different illumination conditions, rigorous electromagnetic simulation calculations of the diffracted focusing light field are implemented by the finite-difference time-domain method. The results show that when the beam waist radius w0 of the illuminating laser is less than the SOL radius a, not only the capability of super-diffraction limit focusing will decrease significantly, but also the intensity of the focal spot will attenuate by more than 50%. Comparing with the amplitude-type SOL, the waist radius w0 has a strong effect on the phase-type SOL and causes a significant focus to shift in the positive direction. However, if w0 is larger than 2a, the ideal focusing characteristics of SOL can be maintained. Under the condition of oblique illumination, the high numerical aperture amplitude-type SOL generally only allows a small inclination angle of less than 10°, while the phase-type SOL has a wide inclination adaptability (can exceed 40°) regardless of the numerical aperture. For the latter, the focal spot will expand laterally and the intensity will decrease sharply with the increase of inclination angle. As for low numerical aperture phase-type SOL, the focusing characteristics, including focal spot size, focusing intensity and the angular position of the focus, can keep stable within an inclination angle of 18°. For imaging infinitely distant objects, the oblique illumination will produce a fluctuating field curvature and significant negative distortion for high numerical aperture SOLs, while for the low numerical aperture SOLs, the field curvature increases with inclination angle increasing and the distortion disappears almost. The research results of this paper provide an important theoretical basis for practical applications of super-oscillatory lens in the fields of sub-diffraction light focusing, super-resolution microscopic imaging, and micro-nano processing of femtosecond laser direct writing.
-
Keywords:
- focusing /
- diffraction /
- micro-nano structure /
- finite-difference time-domain method
[1] Rogers E T F, Lindberg J, Roy T, Savo S, Chad J E, Dennis M R, Zhelidev N I 2012 Nat. Mater. 11 432
Google Scholar
[2] 刘涛 2013 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Liu T 2013 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[3] Francia G T D 1952 IL Nuovo Cimento 9 426
Google Scholar
[4] 邱丽荣 2005 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Qiu L R 2005 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[5] Diao J S, Yuan W Z, Yu Y T, Zhu Y C, Wu Y 2016 Opt. Express 24 1924
Google Scholar
[6] Wu J, Wu Z X, He Y G, Yu A P, Zhang Z H, Wen Z Q, Chen G 2017 Opt. Express 25 6274
Google Scholar
[7] Liu T, Tan J B, Liu J, Wang H T 2013 Opt. Lett. 38 2742
Google Scholar
[8] Liu T, Liu Q, Yang S M, Jiang Z D, Wang T, Zhang G F 2017 Appl. Opt. 56 3725
Google Scholar
[9] Liu T, Tan J B, Liu J, Wang H T 2013 Opt. Express 21 15090
Google Scholar
[10] Liu T, Shen T, Yang S M, Jiang Z D 2015 J. Opt. 17 035610
Google Scholar
[11] Liu T, Liu Q, Yang S M, Jiang Z D, Wang T, Yang X K 2017 Opt. Commun. 393 72
Google Scholar
[12] Yuan G H, Rogers Edward T F, Zheludev N I 2017 Light: Sci. Appl. 6 e17036
Google Scholar
[13] Qin F, Huang K, Wu J F, Teng J H, Qiu C W, Hong M H 2017 Adv. Mater. 29 1602721
Google Scholar
[14] 武靖 2018 硕士学位论文 (重庆: 重庆大学)
Wu J 2018 M. S. Thesis (Chongqing: Chongqing university) (in Chinese)
[15] Nagarajan A, Stoevelaar L P, Silvestri F, et al. 2019 Opt. Express 27 20012
Google Scholar
[16] Liu T, Wang T, Yang S M, Sun L, Jiang Z D 2015 Opt. Express 23 32139
Google Scholar
[17] Yang S M, Wang T, Liu T, Jiang Z D 2016 Opt. Commun. 372 166
Google Scholar
[18] Yu Y T, Li W L, Li H Y, Li M Y, Yuan W Z 2018 Nanomaterials 8 185
Google Scholar
[19] Ni H B, Yuan G H, Sun L D, Chang N, Zhang D, Chen R P, Jiang L Y, Chen H Y, Gu Z Z, Zhao X W 2018 RSC Adv. 8 20117
Google Scholar
[20] Luneburg R K 1966 Mathematical Theory of Optics (Berkeley: University of California Press) p305
[21] Liu T, Yang S M, Jiang Z D 2016 Opt. Express 24 16297
Google Scholar
[22] Chen G, Wu Z X, Yu A P, et al. 2016 Sci. Rep. 6 37776
Google Scholar
[23] 张蕾, 蔡阳健, 陆漩辉 2004 53 1777
Google Scholar
Zhang L, Cai Y J, Lu X H 2004 Acta Phys. Sin. 53 1777
Google Scholar
[24] Rogers E T F, Savo S, Lindberg J, Roy T, Dennis M R, Zheludev N 2013 Appl. Phys. Lett. 102 031108
Google Scholar
[25] 郁道银, 谈恒英 2011 工程光学 (北京: 机械工业出版社) 第118页
Yu D Y, Tan H Y 2011 Engineering Optics (Beijing: China Machine Press) p118 (in Chinese)
-
图 2 SOL1的聚焦光场FDTD计算结果 (a) 轴向光强分布; (b) 焦平面内横向光强分布(Y方向)
Fig. 2. Focused light field of SOL1 by FDTD simulation: (a) On-axis intensity distribution; (b) transverse intensity distribution in the focal plane (Y-direction).
图 3 SOL聚焦性能变化(FDTD) (a) 光斑横向尺寸; (b) 光斑中心强度
Fig. 3. Focusing performance of SOL (FDTD): (a) Transverse size; (b) central intensity.
图 4 SOL2的聚焦光场FDTD计算结果 (a) 轴向光强分布; (b) 焦平面内横向光强分布(Y方向)
Fig. 4. Focused light field of SOL2 by FDTD simulation: (a) On-axis intensity distribution; (b) transverse intensity distribution in the focal plane (Y-direction).
图 5 SOL1聚焦光斑电场分布的FDTD结果 (a) 均匀平面波照明; (b) w0 = a/2的高斯光束照明
Fig. 5. Electric field distribution of SOL1 by FDTD simulation: (a) Uniform plane beam illumination; (b) w0 = a/2 Gaussian beam illumination.
图 6 BG径向偏振光束照明条件下SOL聚焦光场的VAS计算结果 (a), (b) SOL1; (c), (d) SOL2
Fig. 6. Focused light intensity of SOL by VAS calculation under BG radially polarized illumination: (a), (b) SOL1; (c), (d) SOL2.
图 7 SOL对倾斜平行光的衍射聚焦成像示意图
Fig. 7. Schematic diagram of diffraction focused imaging by SOL under oblique illumination.
图 8 倾斜平行光照明的SOL衍射聚焦示意图
Fig. 8. Schematic diagram of diffraction focusing by SOL under oblique illumination.
图 9 振幅型SOL的倾斜照明FDTD聚焦计算结果 (a), (c), (e) SOL5; (b), (d), (f) SOL6
Fig. 9. Focusing results of amplitude-type SOL under oblique illumination: (a), (c), (e) SOL5; (b), (d), (f) SOL6.
图 10 倾斜照明SOL的聚焦光斑尺寸 (a) FWHMx ; (b) FWHMz
Fig. 10. Focal spot size of SOL under oblique illumination: (a) FWHMx ; (b) FWHMz .
图 11 不同照明角度下SOL的聚焦光斑强度
Fig. 11. Focal intensity of SOL varying with oblique illumination angle.
图 12 聚焦光斑角位置变化 (a)
$\omega $ -$\omega '$ 关系曲线; (b)$\omega $ -$\varGamma $ 关系曲线Fig. 12. Angle position of focusing spot: (a)
$\omega $ -$\omega '$ ; (b)$\omega $ -$\varGamma $ .表 1 优化设计的SOL结构参数
Table 1. Structural parameters of optimized SOL.
SOL 类型 ∆r/μm D/μm fsol/μm NA ri /μm ti SOL1 振幅 0.2 16 3.5 0.92 [0.2, 0.4, 1.0, 1.2, 2.0, 2.2, 2.4, 2.6, 3.2,
3.6, 3.8, 4.0, 4.2, 4.6, 4.8, 5.2, 5.4,
6.0, 6.4, 6.8, 7.0, 7.4, 7.6, 8.0][0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1,
0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1]SOL2 相位 0.2 16 3.5 0.92 [0.2, 0.6, 1.0, 1.2, 1.6, 1.8, 2.0, 2.4,
3.0, 3.2, 4.8, 5.0, 5.4, 5.8, 6.2,
6.6, 6.8, 7.2, 7.4, 8.0][–1, 1, –1, 1, –1, 1, –1, 1,
–1, 1, –1, 1, –1, 1,
–1, 1, –1, 1, –1, 1]SOL3 相位 0.2 10 2.0 0.93 [0.473, 0.885, 1.458, 1.969, 2.382,
2.842, 3.044, 4.239, 4.745, 5.000][1, j, 1, j, 1, j, 1, j, 1, j] SOL4 相位 0.2 10 9.9 0.45 [0.268, 0.468, 1.165, 1.365, 1.734,
3.189, 3.399, 4.278, 4.792, 5.000][j, 1, j, 1, j, 1, j, 1, j, 1] SOL5 振幅 0.2 10 1.9 0.93 [0.600, 0.899, 1.915, 2.190, 2.440,
3.756, 4.076, 4.357, 4.769, 5.000][0, 1, 0, 1, 0, 1, 0, 1, 0, 1] SOL6 振幅 0.2 10 10.1 0.44 [0.300, 0.506, 1.248, 1.460, 1.660, 2.885,
3.085, 3.335, 3.755, 4.094, 4.294, 5.000][0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1] 
下载: 导出CSV
-
[1] Rogers E T F, Lindberg J, Roy T, Savo S, Chad J E, Dennis M R, Zhelidev N I 2012 Nat. Mater. 11 432
Google Scholar
[2] 刘涛 2013 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Liu T 2013 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[3] Francia G T D 1952 IL Nuovo Cimento 9 426
Google Scholar
[4] 邱丽荣 2005 博士学位论文 (哈尔滨: 哈尔滨工业大学)
Qiu L R 2005 Ph. D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese)
[5] Diao J S, Yuan W Z, Yu Y T, Zhu Y C, Wu Y 2016 Opt. Express 24 1924
Google Scholar
[6] Wu J, Wu Z X, He Y G, Yu A P, Zhang Z H, Wen Z Q, Chen G 2017 Opt. Express 25 6274
Google Scholar
[7] Liu T, Tan J B, Liu J, Wang H T 2013 Opt. Lett. 38 2742
Google Scholar
[8] Liu T, Liu Q, Yang S M, Jiang Z D, Wang T, Zhang G F 2017 Appl. Opt. 56 3725
Google Scholar
[9] Liu T, Tan J B, Liu J, Wang H T 2013 Opt. Express 21 15090
Google Scholar
[10] Liu T, Shen T, Yang S M, Jiang Z D 2015 J. Opt. 17 035610
Google Scholar
[11] Liu T, Liu Q, Yang S M, Jiang Z D, Wang T, Yang X K 2017 Opt. Commun. 393 72
Google Scholar
[12] Yuan G H, Rogers Edward T F, Zheludev N I 2017 Light: Sci. Appl. 6 e17036
Google Scholar
[13] Qin F, Huang K, Wu J F, Teng J H, Qiu C W, Hong M H 2017 Adv. Mater. 29 1602721
Google Scholar
[14] 武靖 2018 硕士学位论文 (重庆: 重庆大学)
Wu J 2018 M. S. Thesis (Chongqing: Chongqing university) (in Chinese)
[15] Nagarajan A, Stoevelaar L P, Silvestri F, et al. 2019 Opt. Express 27 20012
Google Scholar
[16] Liu T, Wang T, Yang S M, Sun L, Jiang Z D 2015 Opt. Express 23 32139
Google Scholar
[17] Yang S M, Wang T, Liu T, Jiang Z D 2016 Opt. Commun. 372 166
Google Scholar
[18] Yu Y T, Li W L, Li H Y, Li M Y, Yuan W Z 2018 Nanomaterials 8 185
Google Scholar
[19] Ni H B, Yuan G H, Sun L D, Chang N, Zhang D, Chen R P, Jiang L Y, Chen H Y, Gu Z Z, Zhao X W 2018 RSC Adv. 8 20117
Google Scholar
[20] Luneburg R K 1966 Mathematical Theory of Optics (Berkeley: University of California Press) p305
[21] Liu T, Yang S M, Jiang Z D 2016 Opt. Express 24 16297
Google Scholar
[22] Chen G, Wu Z X, Yu A P, et al. 2016 Sci. Rep. 6 37776
Google Scholar
[23] 张蕾, 蔡阳健, 陆漩辉 2004 53 1777
Google Scholar
Zhang L, Cai Y J, Lu X H 2004 Acta Phys. Sin. 53 1777
Google Scholar
[24] Rogers E T F, Savo S, Lindberg J, Roy T, Dennis M R, Zheludev N 2013 Appl. Phys. Lett. 102 031108
Google Scholar
[25] 郁道银, 谈恒英 2011 工程光学 (北京: 机械工业出版社) 第118页
Yu D Y, Tan H Y 2011 Engineering Optics (Beijing: China Machine Press) p118 (in Chinese)
下载:
计量
- 文章访问数: 7200
- PDF下载量: 90
- 被引次数: 0
