-
我们最近证明, 利用红外和深紫外双色激光场, SF6分子的结构信息可以通过其电离谱上的相干条纹获得[arXiv,1912.08499(2019)]. 在本文中, 我们利用该方法考察了两种不同几何结构的分子离子
$ \rm H_3^{2+} $ 在激光场中的直接阈上电离(ATI)过程. 通过与单色激光场中电离谱的比较发现, 双色激光场的电离谱可以分辨分子的不同几何结构. 由相干条件导出的公式可以很好地解释直接ATI动能谱和动量谱中的干涉条纹. 此外, 还发现通过改变分子核间距或改变激光强度可以改变电离谱的形状. 由此可以推断, 双色激光场诱导的ATI谱具有鉴别分子不同构型的能力, 对复杂分子的几何结构成像具有一定的参考意义.-
关键词:
- $ \rm H_3^{2+} $分子 /
- 直接阈上电离(ATI) /
- 不同分子构型
Since imaging the geometrical structure of molecules can help to understand the microscopic world intuitively, and thereby to promote the development of physics, chemistry, material science and biological science, it has long been an important subject for scientists to probe the molecular internal structure. Generally, however, because of the relative complexity of the molecular internal structure, it is difficult to obtain the relevant information by ordinary experimental means. With the development of laser technology, especially the advent of intense ultrafast laser field, ultrafast laser pulse provides an unprecedented detection tool to investigate the related ultrafast dynamics. In recent years, strong field high-order nonlinear ultrafast processes, such as above-threshold ionization(ATI), high-order above-threshold ionization(HATI), high harmonic generation(HHG), and non-sequential double ionization (NSDI), were produced by using femtosecond ultrafast laser to excite molecules. Since the molecules excited in these processes emit the photon and electron signals pertinent to their internal structures, it is natural that one can obtain the imaging of molecular structure by extracting the signals. Recently, we have demonstrated that the structural information of SF6 molecules can be obtained by the interference fringes on the ATI spectrum using the infrared and ultraviolet bichromatic laser fields[arXiv, 1912.08499 (2019)]. In this paper, we use frequency-domian method, which is based on non-perturbed quantum electrodynamics, to investigate the direct above-threshold ionization (ATI) process of triatomic molecular ion$ \rm H_3^{2+} $ with two different geometrical structures by monochromatic and bichromatic laser fields, and given the detailed analysis of the spectra for each case. Compared with the monochromatic laser field, it is found that the ATI spectrum by the bichromatic laser field is more sensitive to the geometrical configuration of molecular ion, thereby it can be applied to identify the different geometrical structure of molecules. In the case of bichromatic laser fields, the direct ATI spectrum show different interference fringes with different molecular configurations. We give the beginning and cutoff curves of each platform by employing the saddle-point approximation. Furthermore, we derive the destructive curves formulas for different molecular configurations in angle-resolved direct ATI energy spectra and momentum spectra, respectively, which carries the information about themolecular structure. In addition, it is found that the shape of the spectra can be modified by changing the molecular internuclear distance or varying the laser intensity. Thereby, it can be inferred that the ATI spectrum induced by bichromatic laser field has the ability to identify different configurations of the same molecules, which is instructive to image geometrical structure of complex molecules.-
Keywords:
- $ \rm H_3^{2+} $ molecular ion /
- direct above threshold ionization (ATI) /
- different molecular configurations
[1] Agostini P, Fabre F, Mainfray G, Petite G, RahmanN K 1979 Phys. Rev. Lett. 42 1127
Google Scholar
[2] Becker W, Liu X, Ho P J, Eberly J H 2012 Rev. Mod.Phys. 84 1011
Google Scholar
[3] SchaferK J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599
Google Scholar
[4] Paulus G G, Nicklich W, Xu H, Lambropoulos P, Walther H 1994 Phys. Rev. Lett. 72 2851
Google Scholar
[5] Walker B, Sheehy B, Kulander K C, DiMauro L F 1996 Phys. Rev. Lett. 77 5031
Google Scholar
[6] Okunishi M, et al. 2008 Phys. Rev. Lett 100 143001
Google Scholar
[7] Li X F, LHuillier A, Ferry M, Lompre L A, Mainfray G 1989 Phys. Rev. A. 39 5751
Google Scholar
[8] LHuillier A, Lompre L A, Mainfray G, Manus C 1992 Adv. At. Mol. Opt. Phys. Suppl. 1 139
[9] Walker B, Sheehy B, DiMauro L F, Agostini P, SchaferK J, Kulander K C 1994 Phys. Rev. Lett. 73 1227
Google Scholar
[10] Becker A, Faisal F H 1999 Phys. Rev. A. 59 R1742
Google Scholar
[11] Meckel M, Comtois D, Zeidler D, et al. 2008 Science 320 5882
[12] Huismans Y, Rouzee A, Gijsbertsen A, et al. 2011 Science 331 6013
[13] Lötstedt E, Midorikawa K 2014 J. Phys. B. 47 204018
Google Scholar
[14] Yuan K, Lu H, Bandrauk A D 2017 J. Phys. B. 50 124004
Google Scholar
[15] Zhou X, Shi S, Li F, Guo Y, Yang Y, Meng Q, Chen J, Liu X and Wang B 2019 arXiv, 1912.08499
[16] Guo D S, Aberg T 1988 J. Phys. A: Math. Gen. 21 4577
Google Scholar
[17] Guo D S, Aberg T, and Crasemann B 1989 Phys. Rev. A. 40 4997
Google Scholar
[18] Gao L, Li X, Fu P, Freeman R R, Guo D S 2000 Phys. Rev A. 61 063407
Google Scholar
[19] Wang B, Gao L, Li X, Guo D S, Fu P 2007 Phys. Rev A. 75 063419
Google Scholar
[20] Kang H, et al. 2010 Phys. Rev. Lett 104 203001
Google Scholar
[21] Wang B , Guo Y, Chen J, Yan Z C, Fu P 2012 Phys. Rev. A 85 023402
Google Scholar
[22] Fu P, Wang B, Li X, Gao L 2001 Phys. Rev. A. 64 063401
Google Scholar
[23] Becker W, Grasbon F, Kopold R, Milosevic D B, Paulus G G, Walther H 2002 Adv. Atom. Mol. Opt. Phys. 48 35
Google Scholar
[24] Shi S, Jin F, Wang B 2019 Chin. Phys. B 28 023202
Google Scholar
[25] Guo D-S, G W F Drake 1992 J. Phys. A: Math. Gen. 25 5377
Google Scholar
[26] Zhang K, Chen J, Hao X L, Fu P, Yan Z C, Wang B 2013 Phys. Rev. A. 88 043435
Google Scholar
-
图 1
$ \rm H_3^{2+} $ 分子的几何构型 (a)线形构型; (b)三角形构型. 核间距为r0 = 2.0 a.u.Fig. 1. Geometrical configuration of
$ \rm H_3^{2+} $ at internuclear distance r0 = 2.0 a.u.: (a) Linear molecule; (b) triangular molecule.
图 2 在单色线性偏振激光场下两种不同几何构型的H32+分子角分辨直接ATI能谱 (a)线形; (b)三角形. 核间距为r0 = 2.0 a.u.
Fig. 2. Angle-resolved direct ATI spectra of H32+molecular ions at internuclear distance r0 = 2.0 a.u. by monochromatic linearly polarized laser fields: (a) Linear; (b) triangular.
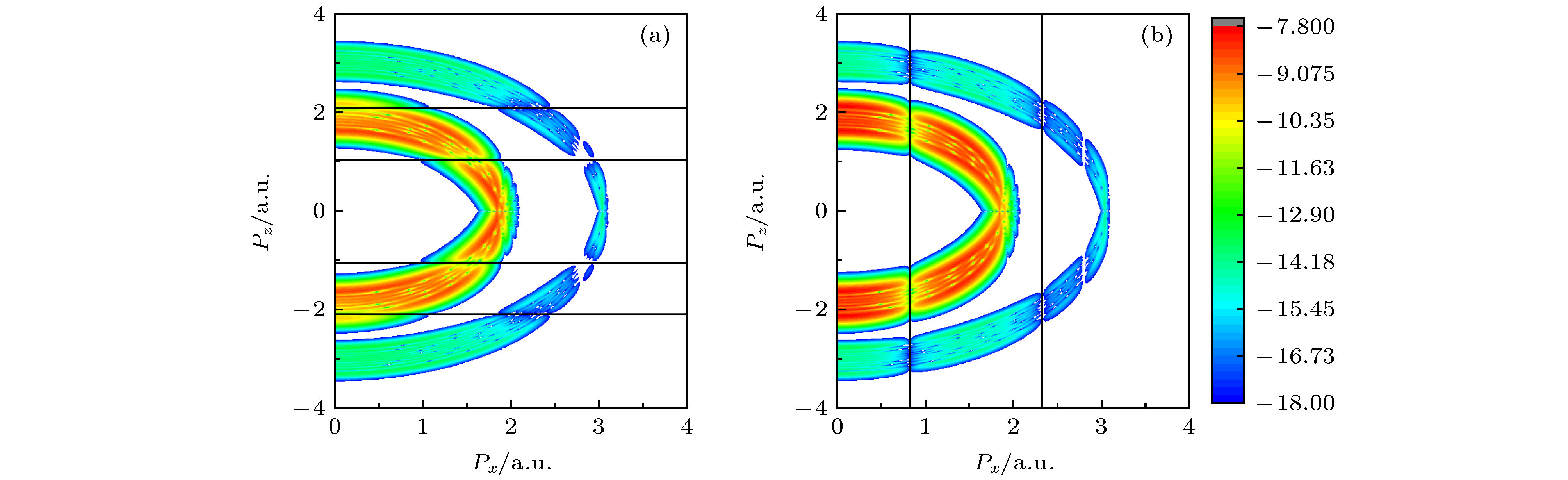
图 3 在双色线性偏振激光场下两种不同几何构型的H32+分子角分辨直接ATI能谱 (a)线形; (b)三角形. 核间距为r0 = 2.0 a.u.,
${t_{c{q_2}}} = {\omega _1}{t_0} ({q_2} = 1, 2)$ Fig. 3. Angle-resolved direct ATI spectra of H32+molecular ions at internuclear distance r0 = 2.0 a.u. by bichromatic linearly polarized laser fields: (a) Linear; (b) triangular. Here,
${t_{c{q_2}}} = {\omega _1}{t_0} ({q_2} = 1, 2)$ .
图 4 在双色线性偏振激光场下两种不同几何构型的
$ \rm H_3^{2+} $ 分子在XZ平面的动量谱 (a)线形; (b)三角形. 核间距为r0 = 2.0 a.u.Fig. 4. The direct ATI momentum spectra of
$ \rm H_3^{2+} $ molecular ions at internuclear distance r0 = 2.0 a.u. by bichromatic linearly polarized laser fields: (a) Linear; (b) triangular.
图 5 在双色线性偏振激光场下两种几何构型的
$ \rm H_3^{2+} $ 分子不同的核间距条件下角分辨直接ATI能谱 (a)−(c)线形; (b)−(f)三角形. (a), (d)核间距为r0 = 1.0 a.u., (b), (e)核间距为r0 = 2.0 a.u., (c), (f)核间距为r0 = 3.0 a.u.Fig. 5. Angle-resolved direct ATI spectra for linear (a)−(c) and triangular (b)−(f)
$ \rm H_3^{2+} $ molecular ions by bichromatic linearly polarized laser field with r0 = 1.0 a.u. (a), (d), r0 = 2.0 a.u. (b), (e), r0 = 3.0 a.u. (c), (f).
图 6 在双色线性偏振激光场下两种几何构型的
$ \rm H_3^{2+} $ 分子不同激光强度条件下角分辨直接ATI能谱 (a)−(c)线形; (b)−(f)三角形. 核间距为r0 = 2.0 a.u., (a), (d)激光强度为${I_1} = {I_2} = 1.0 \times {10^{12}}$ W/cm2, (b), (e)${I_1} = {I_2} = 1.0 \times {10^{13}}$ W/cm2, (c), (f)${I_1} = {I_2} = 1.0 \times {10^{14}}$ W/cm2Fig. 6. Angle-resolved direct ATI spectra for linear (a)−(c) and triangular (b)−(f)
$ \rm H_3^{2+} $ molecular ions with r0 = 2.0 a.u. by bichromatic linearly polarized laser fields. The intensity of laser fields are${I_1} = {I_2} = 1.0 \times {10^{12}}$ W/cm2 (a), (d),${I_1} = {I_2} = 1.0 \times {10^{13}}$ W/cm2 (b), (e),${I_1} = {I_2} = 1.0 \times {10^{14}}$ W/cm2 (c), (f), respectively. -
[1] Agostini P, Fabre F, Mainfray G, Petite G, RahmanN K 1979 Phys. Rev. Lett. 42 1127
Google Scholar
[2] Becker W, Liu X, Ho P J, Eberly J H 2012 Rev. Mod.Phys. 84 1011
Google Scholar
[3] SchaferK J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599
Google Scholar
[4] Paulus G G, Nicklich W, Xu H, Lambropoulos P, Walther H 1994 Phys. Rev. Lett. 72 2851
Google Scholar
[5] Walker B, Sheehy B, Kulander K C, DiMauro L F 1996 Phys. Rev. Lett. 77 5031
Google Scholar
[6] Okunishi M, et al. 2008 Phys. Rev. Lett 100 143001
Google Scholar
[7] Li X F, LHuillier A, Ferry M, Lompre L A, Mainfray G 1989 Phys. Rev. A. 39 5751
Google Scholar
[8] LHuillier A, Lompre L A, Mainfray G, Manus C 1992 Adv. At. Mol. Opt. Phys. Suppl. 1 139
[9] Walker B, Sheehy B, DiMauro L F, Agostini P, SchaferK J, Kulander K C 1994 Phys. Rev. Lett. 73 1227
Google Scholar
[10] Becker A, Faisal F H 1999 Phys. Rev. A. 59 R1742
Google Scholar
[11] Meckel M, Comtois D, Zeidler D, et al. 2008 Science 320 5882
[12] Huismans Y, Rouzee A, Gijsbertsen A, et al. 2011 Science 331 6013
[13] Lötstedt E, Midorikawa K 2014 J. Phys. B. 47 204018
Google Scholar
[14] Yuan K, Lu H, Bandrauk A D 2017 J. Phys. B. 50 124004
Google Scholar
[15] Zhou X, Shi S, Li F, Guo Y, Yang Y, Meng Q, Chen J, Liu X and Wang B 2019 arXiv, 1912.08499
[16] Guo D S, Aberg T 1988 J. Phys. A: Math. Gen. 21 4577
Google Scholar
[17] Guo D S, Aberg T, and Crasemann B 1989 Phys. Rev. A. 40 4997
Google Scholar
[18] Gao L, Li X, Fu P, Freeman R R, Guo D S 2000 Phys. Rev A. 61 063407
Google Scholar
[19] Wang B, Gao L, Li X, Guo D S, Fu P 2007 Phys. Rev A. 75 063419
Google Scholar
[20] Kang H, et al. 2010 Phys. Rev. Lett 104 203001
Google Scholar
[21] Wang B , Guo Y, Chen J, Yan Z C, Fu P 2012 Phys. Rev. A 85 023402
Google Scholar
[22] Fu P, Wang B, Li X, Gao L 2001 Phys. Rev. A. 64 063401
Google Scholar
[23] Becker W, Grasbon F, Kopold R, Milosevic D B, Paulus G G, Walther H 2002 Adv. Atom. Mol. Opt. Phys. 48 35
Google Scholar
[24] Shi S, Jin F, Wang B 2019 Chin. Phys. B 28 023202
Google Scholar
[25] Guo D-S, G W F Drake 1992 J. Phys. A: Math. Gen. 25 5377
Google Scholar
[26] Zhang K, Chen J, Hao X L, Fu P, Yan Z C, Wang B 2013 Phys. Rev. A. 88 043435
Google Scholar
下载:
计量
- 文章访问数: 6221
- PDF下载量: 53
- 被引次数: 0
