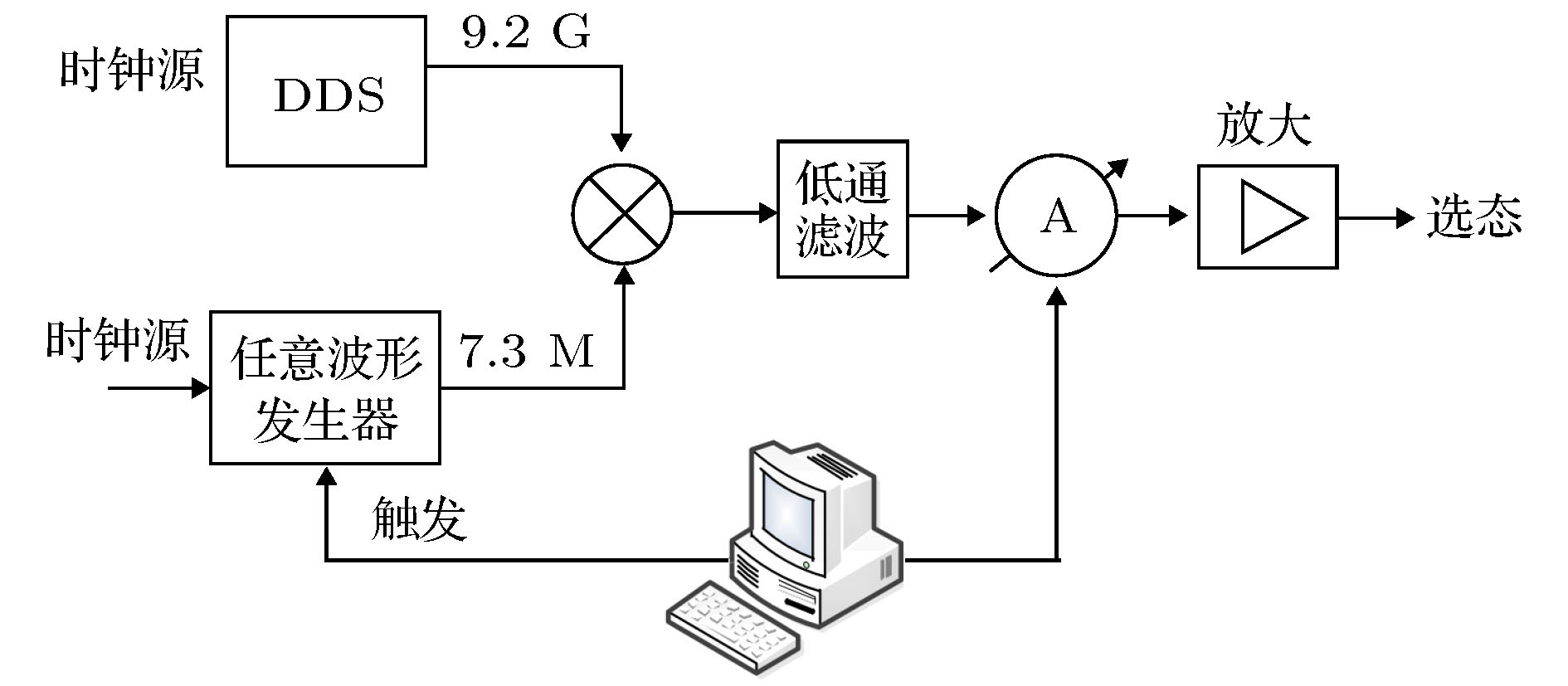
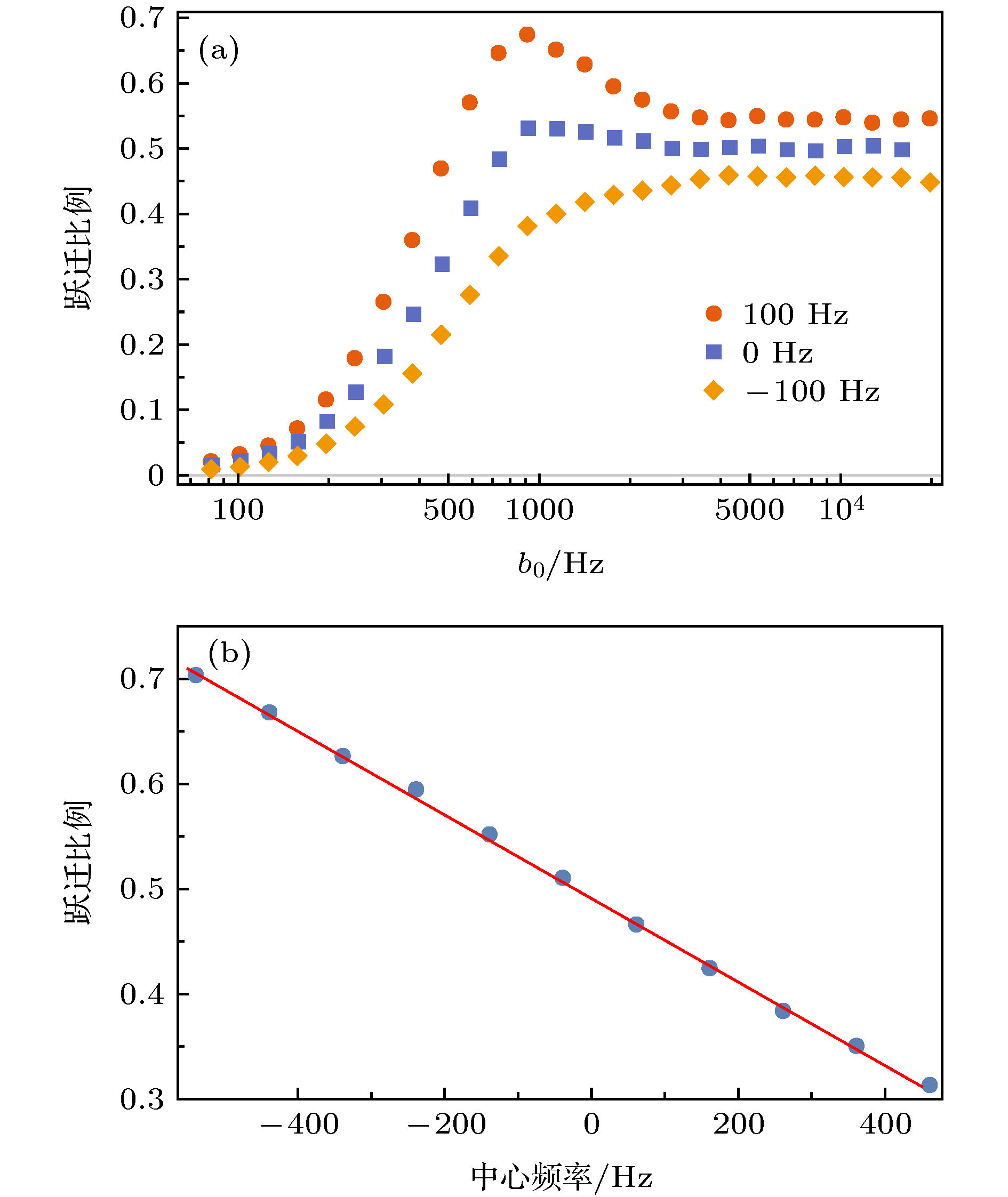
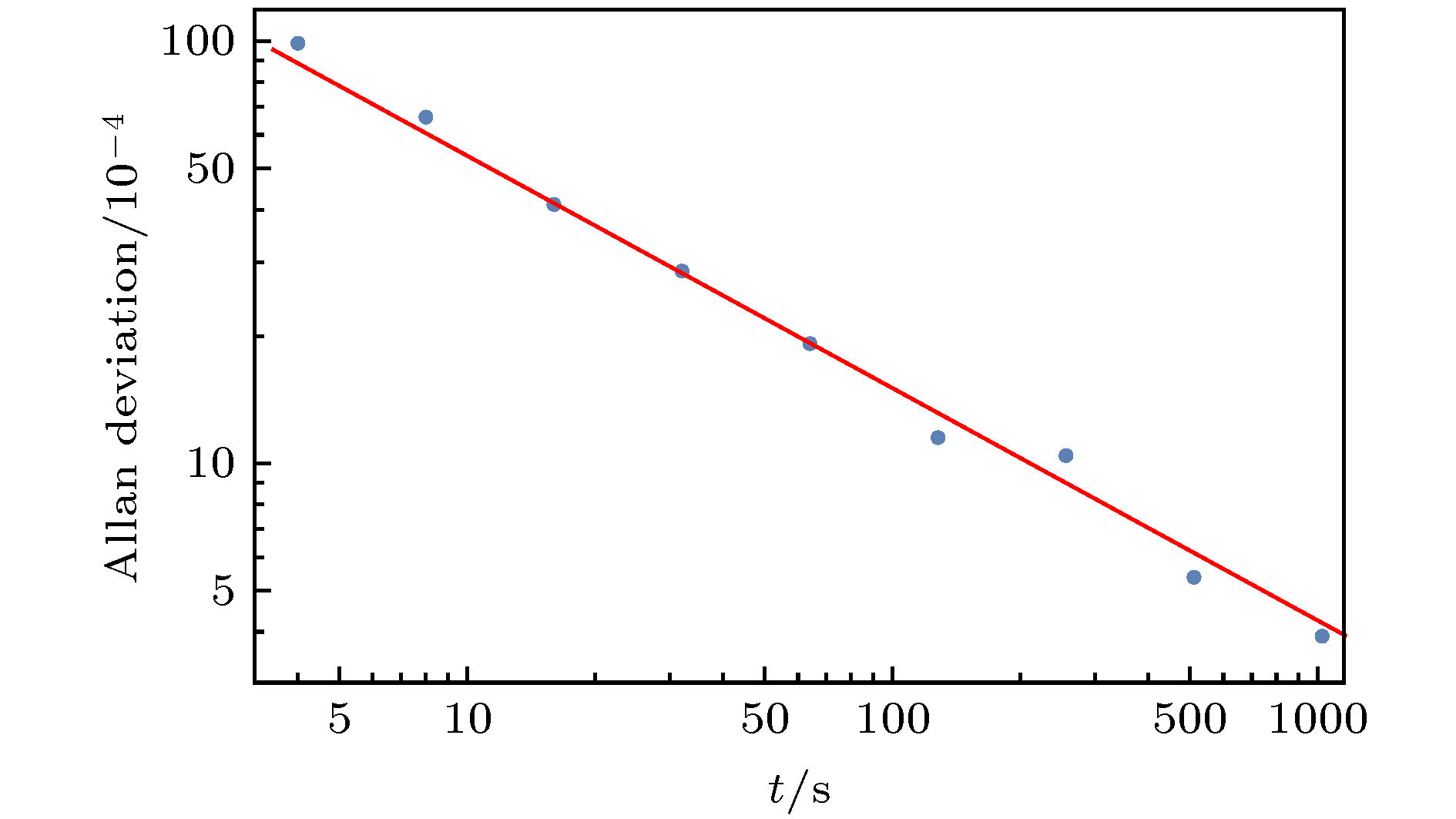
-
Cold collision frequency shift is one of the major systematic effects which limit the frequency uncertainty of the cesium fountain atomic clock. It is proportional to the effective atomic density, which is defined as the average density over the initial spacial and velocity distribution. The measurement of the frequency shift is based on a differential method, in which the fountain clock is operated with two different atomic densities, i.e. high density and low density, in turn. The clock frequency without collision shift can be achieved by linear extrapolation with the frequencies and density ratios of two states. For the density ratio is estimated with the atom number, it plays a crucial role in generating atoms with same density distribution for reducing systematic uncertainty in cold collision frequency shift estimation. The rapid adiabatic passage method is used in Cesium fountain clock to realize homogeneous transition probability, which modulates the amplitude and frequency of microwave continuously to prepare atom sample. To investigate the precision of this method, theoretical analysis and experimental measurement are both used here. An equation of deviation is derived from the time evolution of Bloch vector. The vector rotates at angular speed Ω with the rotation axis processing at lower angular speed. The deviations in the two directions on the surface of Bloch sphere are determined by the equations which are similar to wave equations, and can be simplified into wave equations when the deviations are sufficiently small. It is shown in the equations that the deviations are stimulated by angular velocity and angular acceleration of the precession, and is inversely proportional to the square of Ω. Further calculation shows that the deviation becomes smaller when the amplitude of microwave frequency and Rabi frequency are close to each other. It is then confirmed experimentally. The effects of some other parameters, such as the pulse length and time delay, on transition probability are also measured, showing that the RAP method is insensitive to these parameters up to a large scope. The precision of RAP method is dominated by three factors. The first factor is the product of rotating angular speed Ω and pulse length T, i.e. ΩT: The increase of ΩT can reduce the uncertainty to a satisfactory degree. The second factor is the uncertainty of resonant frequency, so the measurement is required to be precise. The third factor is the unexpected atoms which are not selected by the microwave, and may be attributed to pulling light. After optimizing the parameters, the ratio of low density to high density can approach to 0.5 with 3 × 10–3 uncertainty, which leads to a systematic relative uncertainty of cold collision shift up to 1.6 × 10–16.
-
Keywords:
- cesium fountain atomic clock /
- cold collision frequency shift /
- rapid adiabatic passage method
[1] Li R, Gibble K, Szymaniec K 2011 Metrologia 48 283
Google Scholar
[2] Guena J, Abgrall M, Rovera M, Laurent P, Chupin B, Lours M, Santarelli G, Rosenbusch P, Tobar M E, Li R, Gibble K, Clairon A, Bize S 2012 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 59 391
Google Scholar
[3] Jefferts S R, Shirley J, Parker T E, Heavner T P, Meekhof D M, Nelson C, Levi F, Costanzo G, De Marchi A, Drullinger R, Hollberg L, Lee W D, Walls F L 2002 Metrologia 39 321
Google Scholar
[4] Weyers S, Gerginov V, Nemitz N, Li R, Gibble K 2012 Metrologia 49 82
Google Scholar
[5] 阮军, 王叶兵, 常宏, 姜海峰, 刘涛, 董瑞芳, 张首刚 2015 64 160308
Google Scholar
Ruan J, Wang Y B, Chang H, Jiang H F, Liu T, Dong R F, Zhang S G 2015 Acta Phys. Sin. 64 160308
Google Scholar
[6] 王倩, 魏荣, 王育竹 2018 67 163202
Google Scholar
Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202
Google Scholar
[7] Verhaar B J, Koelman J M V A, Stoof H T C, Luiten O J, Crampton S B 1987 Phys. Rev. A 35 3825
Google Scholar
[8] Tiesinga E, Verhaar B J, Stoof H T C, van Bragt D 1992 Phys. Rev. A 45 R2671
Google Scholar
[9] Kokkelmans S, Verhaar B, Gibble K, Heinzen D 1997 Phys. Rev. A 56 R4389
Google Scholar
[10] Leo P J, Julienne P S, Mies F H, Williams C J 2001 Phys. Rev. Lett. 86 3743
Google Scholar
[11] Sortais Y, Bize S, Nicolas C, Clairon A, Salomon C, Williams C 2000 Phys. Rev. Lett. 85 3117
Google Scholar
[12] Santos F P D, Marion H, Bize S, Sortais Y, Clairon A, Salomon C 2002 Phys. Rev. Lett. 89 233004
Google Scholar
[13] Fertig C, Gibble K 2000 Phys. Rev. Lett. 85 1622
Google Scholar
[14] Heavner T P, Jefferts S R, Shirley J H, Parker T E, Donley E A, Ashby N, Barlow S E, Levi F, Costanzo G 2014 Metrologia 51 174
Google Scholar
[15] Messiah A 1999 Quantum Mechanics (Vol. 2) (New York: Dover) pp740–742
[16] Loy M M T 1974 Phys. Rev. Lett. 32 814
Google Scholar
[17] Marion H 2005 Ph. D. Dissertation (Paris: Université de Paris VI)
[18] Zhang S G 2004 Ph.D. Dissertation (Paris: Université de Paris VI)
[19] Kazda M, Gerginov V, Nemitz N, Weyers S 2013 IEEE Trans. Instrum. Meas. 62 2812
Google Scholar
[20] Kasevich M A, Chu S 1992 Phys. Rev. Lett. 69 1741
Google Scholar
[21] 刘丹丹, 阮军, 管勇, 张辉, 杨帆, 王心亮, 施俊如, 张首刚 2017 时间频率学报 42 107
Liu D D, Ruan J, Guan Y, Zhang H, Yang F, Wang X L, Shi J R, Zhang S G 2017 Journal of Time and Frequency 42 107
-
图 3 脉冲长度8 ms, 脉冲起始点在进入腔后4 ms的跃迁几率 (a) δ0为5 kHz, 不同b0的跃迁几率; (b)功率幅度为10 kHz, 不同δ0的跃迁几率
Fig. 3. Transition probability as a function of b0 and δ0 with 8 ms pulse starts 4 ms after atoms entering the cavity: (a) δ0 = 5 kHz, with different b0; (b) b0 = 10 kHz, with different δ0.
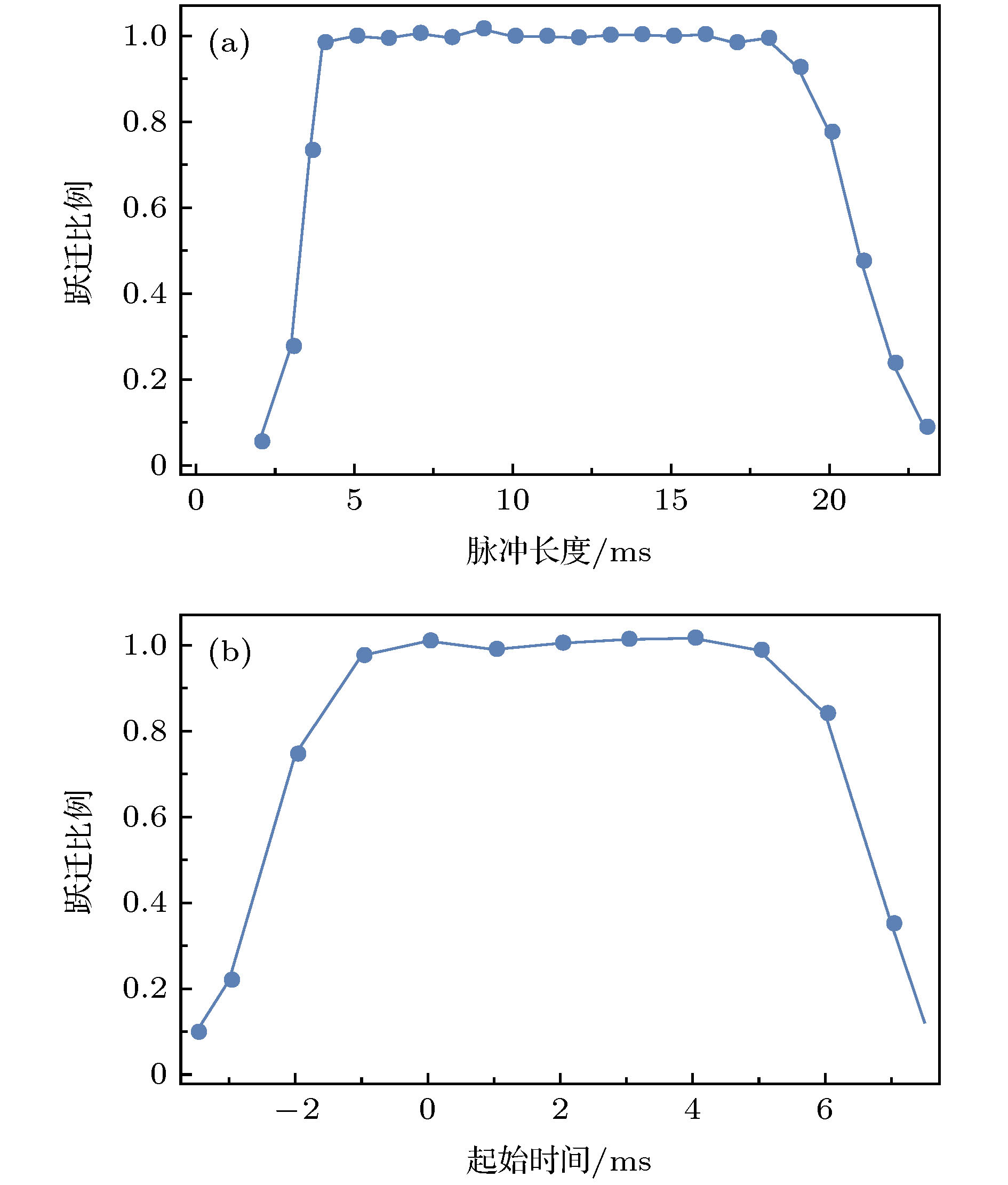
图 5 时间参数对跃迁比例的影响, 其中δ0 = 5 kHz, b0 = 10 kHz. 以原子到达选态腔下端面为时间0点 (a)固定脉冲以原子在腔中心的时间点为中心, 改变脉冲长度; (b)固定脉冲长度为8 ms, 改变脉冲起始时间
Fig. 5. Transition probability as a function of time parameters, δ0 = 5 kHz, b0 = 10 kHz, atoms enter selection cavity at time 0: (a) Pulse duration remaining symmetric about the central point of cavity; (b) start point of pulse with a fixed duration of 8 ms.
图 6 不同频率中心值的跃迁几率
Fig. 6. Transition probabilty as a function of center frequency detuning.
图 7 δ0 = 5 kHz, 脉冲开始于不同时刻, 结束于入腔后10 ms. 5个不同脉冲长度下, 不同b0的跃迁几率 (a)横坐标为b0; (b)横坐标为b0与脉冲长度T的乘积
Fig. 7. Transition probability as a function of b0 for a 5 kHz δ0 pulse start at 5 different points and end at 10 ms after entering cavity: (a) b0 as the abscissa; (b) b0T as the abscissa.
图 8 (a)在5个δ0下, 不同b0的跃迁几率; (b)脉冲频率幅度为5 kHz, b0为10 kHz, 不同脉冲长度的跃迁几率
Fig. 8. Transition probability as a function of (a) b0 for five different δ0, (b) pulse duration with δ0 = 5 kHz, and b0 = 10 kHz.
图 9 (a)中心频率取100, 0, –100 Hz, 不同b0时的跃迁几率; (b)δ0 = 5 kHz, b0 = 10 kHz时, 不同中心频率的跃迁几率
Fig. 9. (a) Transition probability as a function of b0 for 100, 0, –100 Hz center frequency detuning; (b) transition probability as a function of center frequency detuning for δ0 = 5 kHz and b0 = 10 kHz.
-
[1] Li R, Gibble K, Szymaniec K 2011 Metrologia 48 283
Google Scholar
[2] Guena J, Abgrall M, Rovera M, Laurent P, Chupin B, Lours M, Santarelli G, Rosenbusch P, Tobar M E, Li R, Gibble K, Clairon A, Bize S 2012 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 59 391
Google Scholar
[3] Jefferts S R, Shirley J, Parker T E, Heavner T P, Meekhof D M, Nelson C, Levi F, Costanzo G, De Marchi A, Drullinger R, Hollberg L, Lee W D, Walls F L 2002 Metrologia 39 321
Google Scholar
[4] Weyers S, Gerginov V, Nemitz N, Li R, Gibble K 2012 Metrologia 49 82
Google Scholar
[5] 阮军, 王叶兵, 常宏, 姜海峰, 刘涛, 董瑞芳, 张首刚 2015 64 160308
Google Scholar
Ruan J, Wang Y B, Chang H, Jiang H F, Liu T, Dong R F, Zhang S G 2015 Acta Phys. Sin. 64 160308
Google Scholar
[6] 王倩, 魏荣, 王育竹 2018 67 163202
Google Scholar
Wang Q, Wei R, Wang Y Z 2018 Acta Phys. Sin. 67 163202
Google Scholar
[7] Verhaar B J, Koelman J M V A, Stoof H T C, Luiten O J, Crampton S B 1987 Phys. Rev. A 35 3825
Google Scholar
[8] Tiesinga E, Verhaar B J, Stoof H T C, van Bragt D 1992 Phys. Rev. A 45 R2671
Google Scholar
[9] Kokkelmans S, Verhaar B, Gibble K, Heinzen D 1997 Phys. Rev. A 56 R4389
Google Scholar
[10] Leo P J, Julienne P S, Mies F H, Williams C J 2001 Phys. Rev. Lett. 86 3743
Google Scholar
[11] Sortais Y, Bize S, Nicolas C, Clairon A, Salomon C, Williams C 2000 Phys. Rev. Lett. 85 3117
Google Scholar
[12] Santos F P D, Marion H, Bize S, Sortais Y, Clairon A, Salomon C 2002 Phys. Rev. Lett. 89 233004
Google Scholar
[13] Fertig C, Gibble K 2000 Phys. Rev. Lett. 85 1622
Google Scholar
[14] Heavner T P, Jefferts S R, Shirley J H, Parker T E, Donley E A, Ashby N, Barlow S E, Levi F, Costanzo G 2014 Metrologia 51 174
Google Scholar
[15] Messiah A 1999 Quantum Mechanics (Vol. 2) (New York: Dover) pp740–742
[16] Loy M M T 1974 Phys. Rev. Lett. 32 814
Google Scholar
[17] Marion H 2005 Ph. D. Dissertation (Paris: Université de Paris VI)
[18] Zhang S G 2004 Ph.D. Dissertation (Paris: Université de Paris VI)
[19] Kazda M, Gerginov V, Nemitz N, Weyers S 2013 IEEE Trans. Instrum. Meas. 62 2812
Google Scholar
[20] Kasevich M A, Chu S 1992 Phys. Rev. Lett. 69 1741
Google Scholar
[21] 刘丹丹, 阮军, 管勇, 张辉, 杨帆, 王心亮, 施俊如, 张首刚 2017 时间频率学报 42 107
Liu D D, Ruan J, Guan Y, Zhang H, Yang F, Wang X L, Shi J R, Zhang S G 2017 Journal of Time and Frequency 42 107
下载:
计量
- 文章访问数: 6790
- PDF下载量: 67
- 被引次数: 0
