-
When it reaches high energy density state, new features of laser propagation in plasma arises in the contrast to that of research field in classical optics. Such as beam deflection, a laser beam can change its propagation direction while it comes across a transverse plasma flow. On the other hand, employment of all sorts of smoothed laser beams becomes very common in high power laser facilities for high energy density physics experiments. Therefore, on what condition beam deflection comes into play for smoothed beams are necessary to be investigated. This paper presents numerical simulation results for that, which is performed by laser plasma interaction code LAP3D. It is a three dimensional massively parallel code, including a laser paraxial envelope solver and a nonlinear Eulerian hydrodynamics package, and models for filamentation, stimulated Raman scattering and stimulated Brillouin scattering, with beam smoothed by continuous phase plate (CPP), spectral dispersion (SSD), separately. For simplicity in this study, numerical simulations perform in a about 700 μm × 700 μm × 700 μm plasma using isotropic conditions (Te = 3 keV, Ti = 1 keV, n = 0.1 nc) and only include refraction and diffraction effects, namely, with filamentation model excluding scattering models. Simulation employs the CPP and the SSD beam as representatives of spatial and temporal smoothed beams, respectively, and uses an oval like focused spot with extension in the long axis direction about 200 μm in the focus plane propagating through the left boundary into the simulation domain. Based on our previous investigations, we assume that beam deflection of a smoothed beam becomes effective when it satisfies two following conditions as that for a Gaussian beam, namely, suffering filamentation and facing a transverse plasma flow at ion sound speed. Simulation results of LAP3D confirm that both spatial and temporal smoothed beams suffer beam deflection when two above conditions are both satisfied. For the case of CPP smoothed beam, simulation results show that it suffers evident beam deflection under the conditions that it suffers filamentation when its average intensity is larger than that of filamentation threshold, and faces a transverse plasma flow at ion sound speed. For the case of SSD smoothed beam, simulation results show that the beam can avoid beam deflection even if it faces a transverse plasma flow at ion sound speed when filamentation is suppressed as beam bandwidth is much larger than the growth rate of filamentation, otherwise it suffers beam deflection.
-
Keywords:
- high energy density physics /
- beam propagation /
- smoothed beam /
- beam deflection
[1] Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339
Google Scholar
[2] 德雷克 著 (孙承纬 译) 2013 高能量密度物理基础、惯性约束聚变和实验天体物理学(北京: 国防工业出版社) 第245—286页
Drake R P (translated by Sun C W) 2013 High-Energy-Density Physics Fundamentals, Inertial Fusion, and Experimental Astrophysics (Beijing: National Defense Industry Press) pp245−286 (in Chinese)
[3] Montgomery D S 2016 Phys. Plasmas 23 055601
Google Scholar
[4] Kirkwood R K, Moody J D, Kline J, Dewald E, Glenzer S, Divol L, Michel P, Hinkel D, Berger R, Williams E, Milovich J, Yin L, Rose H, MacGowan B, Landen O, Rosen M, Lindl J 2013 Plasma Phys. Control. Fusion 55 103001
Google Scholar
[5] 张家泰 1999 激光等离子体相互作用物理与模拟(郑州: 河南科学技术出版社) pp269−316
Zhang J T 1999 Physics and Simulations of Laser Plasma Interactions (Zhengzhou: Henan Science and Technology Press) 第269—316页 (in Chinese)
[6] Moody J D, MacGowan B J, Rothenberg J E, Berger R L, Young P E 2001 Phys. Rev. Lett. 86 2810
Google Scholar
[7] Craxton R S, Anderson K S, Boehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty P W, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[8] 周煜梁, 隋展, 刘兰琴, 粟敬钦, 李平, 张锐, 许立新, 王文义, 莫磊 2011 激光与光电子学进展 48 101407
Zhou Y L, Sui Z, Liu L Q, Su J Q, Li P, Zhang R, Xu L X, Wang W Y, Mo L 2011 Laser & Optoelectronics Progress 48 101407
[9] Young P E, Still C H, Hinkel D E, Kruer W L, Estabrook K G 1998 Phys. Rev. Lett. 81 1425
Google Scholar
[10] Moody J D, MacGowan B J, Hinkel D E, Kruer W L, Williams E A, Estabrook K, Berger R L, Kirkwood R K, Montgomery D S, Shepard T D 1996 Phys. Rev. Lett. 77 1294
Google Scholar
[11] 李斌, 刘占军, 郑春阳, 胡晓燕 2014 强激光与离子束 26 122005
Google Scholar
Li B, Liu Z J, Zheng C Y, Hu X Y 2014 High Power Laser and Particle Beams 26 122005
Google Scholar
[12] Hu X Y, Hao L, Liu Z J, Zheng C Y, Li B, Guo H 2015 AIP Advances 5 087174
Google Scholar
[13] Liu Z J, Li B, Hu X Y, Xiang J, Zheng C Y, Cao L H, Hao L 2016 Phys. Plasmas 23 022705
Google Scholar
[14] 李平, 马驰, 粟敬钦, 程文雍, 刘兰琴, 王文义, 莫磊, 周丽丹 2008 强激光与粒子束 20 1114
Li P, Ma C, Su J Q, Cheng W Y, Liu L Q, Wang W Y, Mo L, Zhou L D 2008 High Power Laser and Particle Beams 20 1114
[15] 李斌, 胡晓燕, 郑春阳, 刘占军 2016 强激光与离子束 28 112004
Li B, Hu X Y, Zheng C Y, Liu Z J 2016 High Power Laser and Particle Beams 28 112004
[16] 李斌, 刘占军, 郝亮, 胡晓燕, 郑春阳, 项江 2017 中国激光 44 1201004
Google Scholar
Li B, Liu Z J, Hao L, Hu X Y, Zheng C Y, Xiang J 2017 Chinese J. Lasers 44 1201004
Google Scholar
[17] Kruer W L 2003 The Physics of Laser Plasma Interactions (Colorado: Westview Press) pp70–71
[18] Tomson J J, Kruer W L, Bodner S E, DeGroot J S 1974 Phys. Fluids 17 849
Google Scholar
[19] Valeo E J, Oberman C 1973 Phys. Rev. Lett. 30 1035
Google Scholar
[20] Thomson J J, Karush J I 1974 Phys. Fluids 17 1608
Google Scholar
[21] Williams E A, Albitton J R, Rosenbluth M N 1979 Phys. Fluids 22 139
Google Scholar
-
图 1 不同激光强度下空间束匀滑光束对应的束偏折模拟结果 (a) Φ200模型2加横向流; (b) Φ200模型5加横向流. 图中横纵坐标对应模拟空间坐标z和x, 其量纲为激光波长. 横向流速等于离子声速
Fig. 1. Beam deflection simulation results at different incident intensity: (a) Transverse flow and average intensity lower than filamentation threshold; (b) transverse flow and average intensity higher than filamentation threshold. x and yaxes of two figures corresponding to xand z axes of simulation coordinates, respectively. The spatial scale is in unit of laser wave length. The transverse flow speed equals ion sound speed.
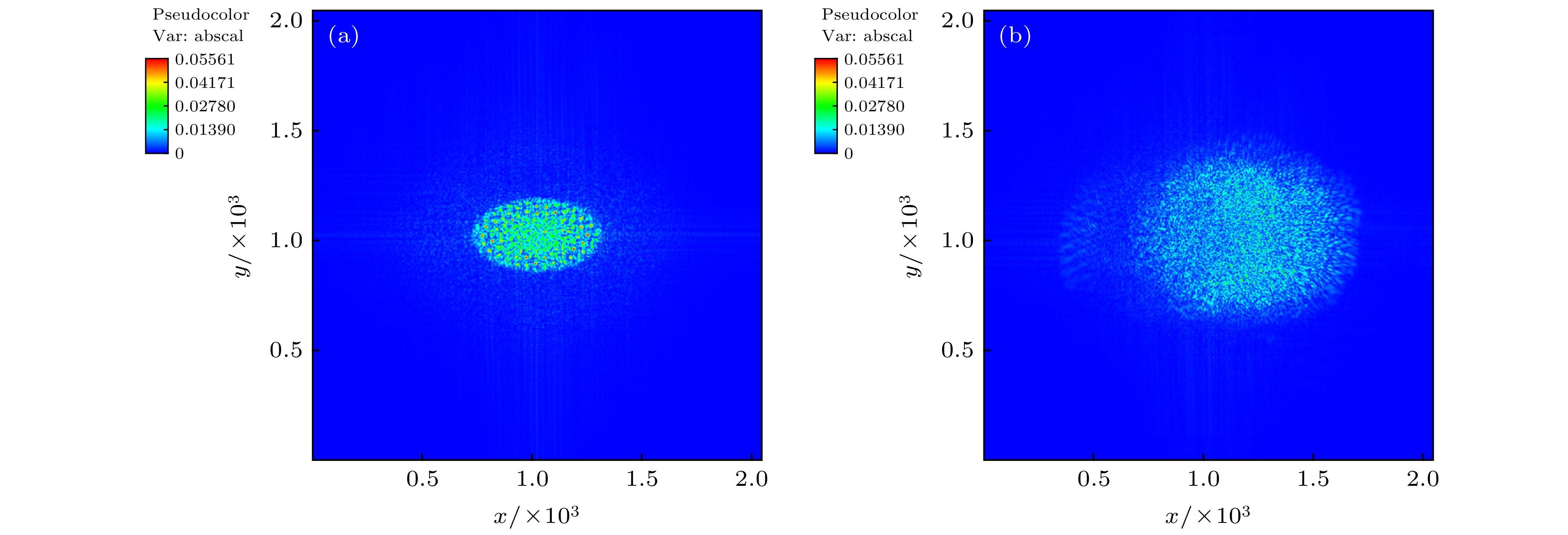
图 2 对比空间束匀滑光束发生束偏折时Φ200模型5加横向流的入射面和出射面内光斑电场幅值分布 (a)入射面; (b)出射面. 图中横纵坐标对应模拟空间坐标x和y, 其量纲为激光波长. 横向流速等于离子声速
Fig. 2. Comparison of spatial distribution of laser electric field between laser entrance and exit planes as beam deflection presents: (a) Laser entrance plane; (b) laser exit plane. x and y axes of two figures corresponding to x and y axes of simulation coordinates, respectively. The spatial scale is in unit of laser wave length. The transverse flow speed equals ion sound speed.
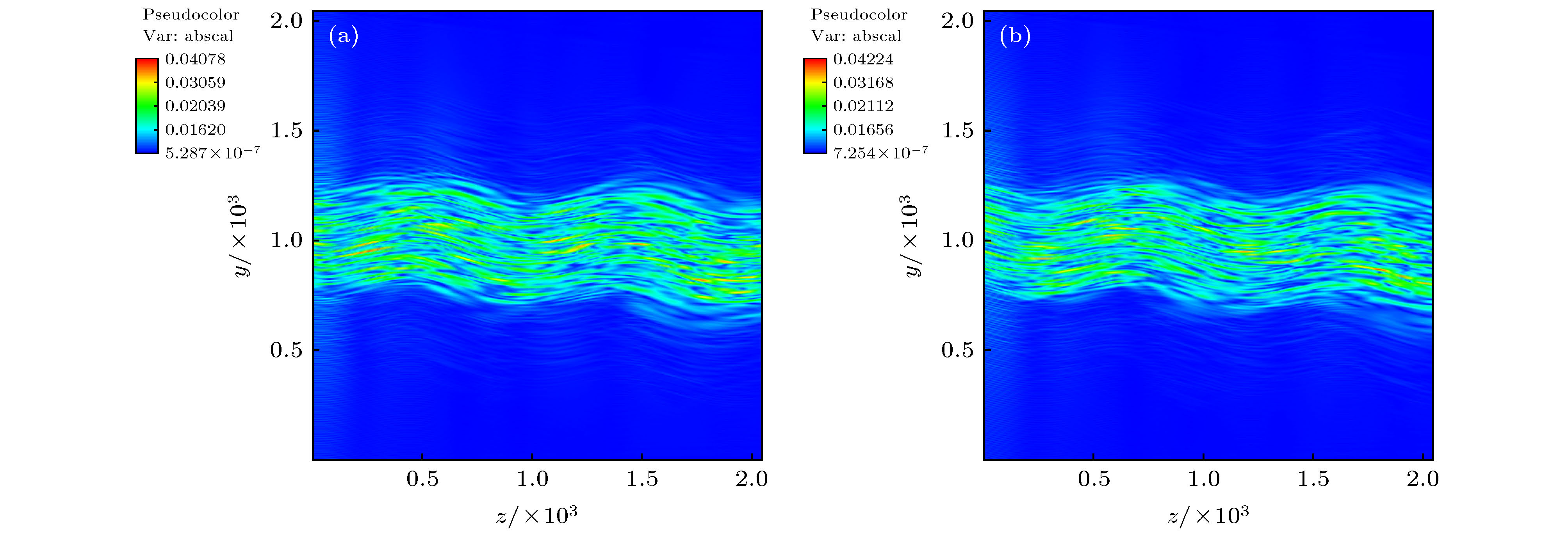
图 3 调制频率为
${10^{ - 3}}{\omega _0}$ 的时间束匀滑光束传播行为 (a)对应11000激光周期; (b)对应13750激光周期. 图中横纵坐标对应模拟空间坐标z和y, 其量纲为激光波长Fig. 3. Propagation of SSD beam at modulation frequency of 10–3ω0: (a) Corresponding simulation result at 11000 th laser periods; (b) corresponding simulation result at 13750 th laser periods. x and y axes of two figures corresponding to z and y axes of simulation coordinates, respectively. The spatial scale is in unit of laser wave length.
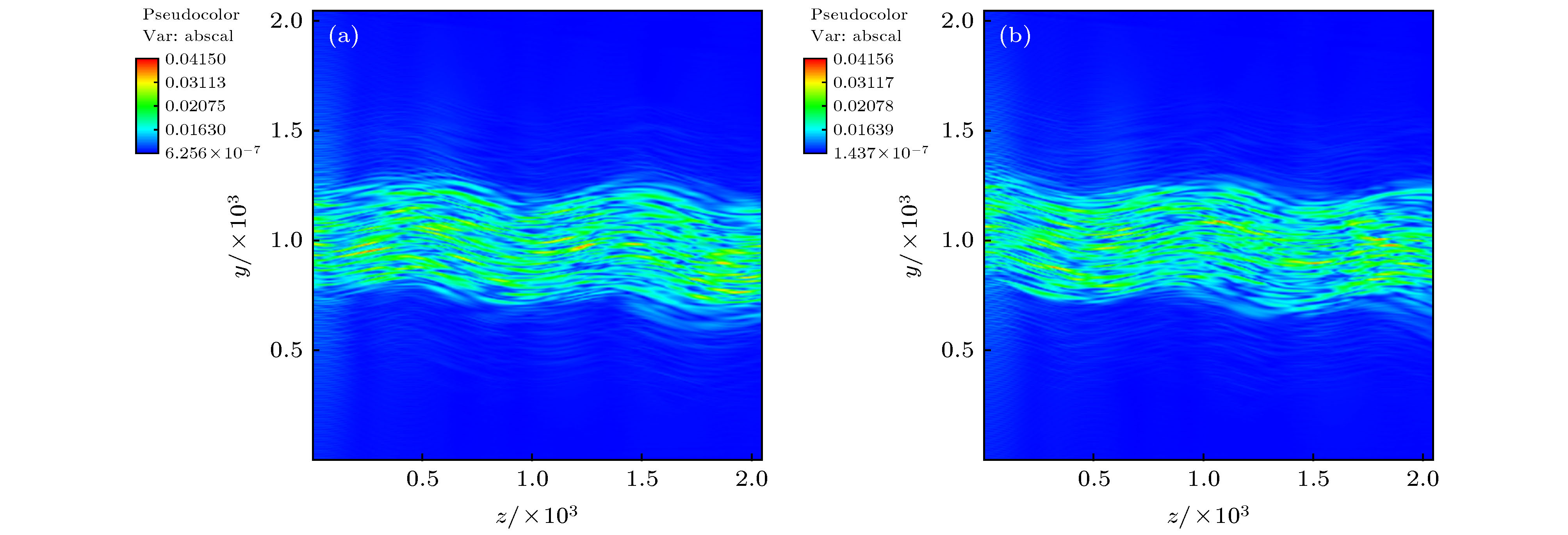
图 4 有横向离子声速量级等离子体流时调制频率为
${10^{ - 3}}{\omega _0}$ 的时间束匀滑光束的传播行为 (a)对应11000激光周期; (b)对应13750激光周期. 图中横纵坐标对应模拟空间坐标z和y, 其量纲为激光波长. 横向流速等于离子声速Fig. 4. Propagation of SSD beam with transverse flow at modulation frequency of 10–3 ω0: (a) Corresponding simulation result at 11000 th laser periods; (b) corresponding simulation result at 13750th laser periods. x and y axes of two figures corresponding to z and y axes of simulation coordinates, respectively. The spatial scale is in unit of laser wave length. The transverse flow speed equals ion sound speed.
图 5 对比时间束匀滑光束在调制频率为
${10^{ - 4}}{\rm{ }}{\omega _0}$ 时的光束传播行为 (a)等离子体横向流速为零; (b)等离子体横向流速等于离子声速. 图中横纵坐标对应模拟空间坐标y和z, 其量纲为激光波长Fig. 5. Propagation of SSD beam at modulation frequency of 10–4ω0: (a) No transverse flow; (b) the transverse flow speed equals ion sound speed. x and y axes of two figures corresponding to y and z axes of simulation coordinates, respectively. The spatial scale is in unit of laser wave length.
表 1 空间束匀滑光束Φ200成丝和束偏折现象模拟结果
Table 1. Simulation results for filamentaion and beam deflection in the case of CPP smoothed beam Φ200.
模型 光斑平均强度/${\rm{W} } \cdot {\rm{c} }{ {\rm{m} }^{ {\rm{ - 2} } } }$ 成丝现象 束偏折现象 1 4.30 × 1013 否 否 2 3.86 × 1014 否 否 3 1.07 × 1015 是 是 4 2.11 × 1015 是 是 5 3.49 × 1015 是 是 
下载: 导出CSV
-
[1] Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339
Google Scholar
[2] 德雷克 著 (孙承纬 译) 2013 高能量密度物理基础、惯性约束聚变和实验天体物理学(北京: 国防工业出版社) 第245—286页
Drake R P (translated by Sun C W) 2013 High-Energy-Density Physics Fundamentals, Inertial Fusion, and Experimental Astrophysics (Beijing: National Defense Industry Press) pp245−286 (in Chinese)
[3] Montgomery D S 2016 Phys. Plasmas 23 055601
Google Scholar
[4] Kirkwood R K, Moody J D, Kline J, Dewald E, Glenzer S, Divol L, Michel P, Hinkel D, Berger R, Williams E, Milovich J, Yin L, Rose H, MacGowan B, Landen O, Rosen M, Lindl J 2013 Plasma Phys. Control. Fusion 55 103001
Google Scholar
[5] 张家泰 1999 激光等离子体相互作用物理与模拟(郑州: 河南科学技术出版社) pp269−316
Zhang J T 1999 Physics and Simulations of Laser Plasma Interactions (Zhengzhou: Henan Science and Technology Press) 第269—316页 (in Chinese)
[6] Moody J D, MacGowan B J, Rothenberg J E, Berger R L, Young P E 2001 Phys. Rev. Lett. 86 2810
Google Scholar
[7] Craxton R S, Anderson K S, Boehly T R, Goncharov V N, Harding D R, Knauer J P, McCrory R L, McKenty P W, Meyerhofer D D, Myatt J F, Schmitt A J, Sethian J D, Short R W, Skupsky S, Theobald W, Kruer W L, Tanaka K, Betti R, Collins T J B, Delettrez J A, Hu S X, Marozas J A, Maximov A V, Michel D T, Radha P B, Regan S P, Sangster T C, Seka W, Solodov A A, Soures J M, Stoeckl C, Zuegel J D 2015 Phys. Plasmas 22 110501
Google Scholar
[8] 周煜梁, 隋展, 刘兰琴, 粟敬钦, 李平, 张锐, 许立新, 王文义, 莫磊 2011 激光与光电子学进展 48 101407
Zhou Y L, Sui Z, Liu L Q, Su J Q, Li P, Zhang R, Xu L X, Wang W Y, Mo L 2011 Laser & Optoelectronics Progress 48 101407
[9] Young P E, Still C H, Hinkel D E, Kruer W L, Estabrook K G 1998 Phys. Rev. Lett. 81 1425
Google Scholar
[10] Moody J D, MacGowan B J, Hinkel D E, Kruer W L, Williams E A, Estabrook K, Berger R L, Kirkwood R K, Montgomery D S, Shepard T D 1996 Phys. Rev. Lett. 77 1294
Google Scholar
[11] 李斌, 刘占军, 郑春阳, 胡晓燕 2014 强激光与离子束 26 122005
Google Scholar
Li B, Liu Z J, Zheng C Y, Hu X Y 2014 High Power Laser and Particle Beams 26 122005
Google Scholar
[12] Hu X Y, Hao L, Liu Z J, Zheng C Y, Li B, Guo H 2015 AIP Advances 5 087174
Google Scholar
[13] Liu Z J, Li B, Hu X Y, Xiang J, Zheng C Y, Cao L H, Hao L 2016 Phys. Plasmas 23 022705
Google Scholar
[14] 李平, 马驰, 粟敬钦, 程文雍, 刘兰琴, 王文义, 莫磊, 周丽丹 2008 强激光与粒子束 20 1114
Li P, Ma C, Su J Q, Cheng W Y, Liu L Q, Wang W Y, Mo L, Zhou L D 2008 High Power Laser and Particle Beams 20 1114
[15] 李斌, 胡晓燕, 郑春阳, 刘占军 2016 强激光与离子束 28 112004
Li B, Hu X Y, Zheng C Y, Liu Z J 2016 High Power Laser and Particle Beams 28 112004
[16] 李斌, 刘占军, 郝亮, 胡晓燕, 郑春阳, 项江 2017 中国激光 44 1201004
Google Scholar
Li B, Liu Z J, Hao L, Hu X Y, Zheng C Y, Xiang J 2017 Chinese J. Lasers 44 1201004
Google Scholar
[17] Kruer W L 2003 The Physics of Laser Plasma Interactions (Colorado: Westview Press) pp70–71
[18] Tomson J J, Kruer W L, Bodner S E, DeGroot J S 1974 Phys. Fluids 17 849
Google Scholar
[19] Valeo E J, Oberman C 1973 Phys. Rev. Lett. 30 1035
Google Scholar
[20] Thomson J J, Karush J I 1974 Phys. Fluids 17 1608
Google Scholar
[21] Williams E A, Albitton J R, Rosenbluth M N 1979 Phys. Fluids 22 139
Google Scholar
下载:
计量
- 文章访问数: 5517
- PDF下载量: 64
- 被引次数: 0
